Keerthana Srikumar - lambdageeks.com

How To Find Acceleration With Coefficient Of Friction: Comprehensive Methods and Insights

January 21, 2024December 18, 2021 by Keerthana Srikumar

How to find acceleration with coefficient of friction is another important and conventional topic that needs to be dealt with. It is a factor that enhances acceleration in a particular way possible.

When a body is in motion, it will continue to in the same until a force acts upon it that changes the object’s dimensions. So this process will go on unless a speed is increased or decreased.

Once the object changes speed, it will either be accelerated (positive) or decelerated (negative), usually in the opposite direction of the action of motion. The change in speed is also known as velocity in physics terms.

The change in speed happens at a different time, and hence this will influence the acceleration of the body in motion either positively or negatively. A sudden jerk in the system gives the acceleration a change also.

When a body is under motion, there are several factors that influence and one of those is acceleration, which will be affected by the term called friction. Slowly we will be dealing with finding acceleration with coefficient of friction.

We can keep talking about acceleration in so many ways, but when another factor affects the acceleration, we need to focus on that. Friction is fundamentally the factor present between the body and the active surface.

Understanding of friction and coefficient of fiction

Let’s first understand friction and the coefficient of friction before diving into detail. Friction is the force that opposes motion, whether in walking, running, or other activities. It arises from a factor present between an object and the surface, known as the frictional force, which enables movement.

Friction varies with the surface texture: it’s higher on rough surfaces and lower on smooth ones. Consequently, as friction increases, acceleration decreases, and vice versa. This basic principle is fundamental in understanding motion.

Now, what is the coefficient of friction? It’s a dimensionless ratio of the normal force to the frictional force, influencing a body in motion. It plays a pivotal role in determining how much force is needed to move an object.

Several factors contribute to a body’s movement, primarily the change in speed, or velocity. The overall net force, which includes external forces and friction, significantly affects movement. The coefficient of friction quantifies this effect.

Being a ratio, the coefficient of friction is dimensionless. Its value typically ranges from a minimum of 0 to a maximum of around 0.5, although it can exceed 1 in some cases. Understanding this coefficient is crucial for comprehending the forces required for the motion of any object.

How to find acceleration with coefficient of friction

Knowledge about the formula to find the acceleration is required. As per Newton’s Second Law, the acceleration is proportional to the force and indirectly proportional to the mass of the object.

Hence, we derive it as a = F / m. this is the formula for basic acceleration without any attributes. When friction is acting upon the body and motion of it, the type of surface is also equally important.

So the formula is changed according to the coefficient of friction, $a = (\frac{f_n - \mu}{m}). μ$ is known as the coefficient of friction, and this will indicate the amount of force required to move the body further in motion.

Let us see how this is using a better example. Rightward friction of 10N is applied on a 7kg weighing body. It is allowed to accelerate on a rough surface. The force of friction has a value of 0.3N. Now calculate the acceleration of the object.

a = (20 – 0.3) / 7

a = 19.7/7

a = 2.81 ms-2

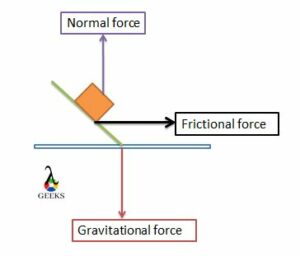
So this is how to find acceleration with coefficient of friction. But where the use of coefficient of friction is is the question. We will deal with that too. In the question, the friction force constant is directly given.

The frictional force and the force of normal will not be given explicitly but using friction coefficient the values can be drawn. From the data given, we must calculate the coefficient of friction to apply it to the formula and find the acceleration.

Problem on how to find acceleration with coefficient of friction

Problem:

An 1100kg of the car with a coefficient of friction having value μ = 0.95 concerning the tires. Now determine the acceleration. It moves with a force of 880N.

Solution:

We need to understand this problem using a free-body diagram. Now let us dive into the motion of the car and the kind of forces acting upon it. Since the car is in motion, it will experience as many forces as possible.

We know that by default, a normal force acts on the body; now, since it is in motion, a frictional force acts as well.

The value given for the coefficient of friction is μ = 0.95. Here we need to find the frictional and normal forces since the coefficient of friction value is already given.

We need to note that normal force is equal to the gravitational force. It is known that the force of gravity is 9.8ms-1. And now, that value multiplied by the mass gives the normal force. Fn= 1100×9.8 = 10780.

Force of friction is the coefficient of friction times the normal force. Hence ff =10241. Now that force of friction is found next step is to find the acceleration. The frictional force is also considered as the net force.

a= f/m

a= 10241/1100

a= 9.31ms-2

Frequently Asked Questions

How do you find velocity with friction?

Since acceleration could be found with friction, velocity could also be found since it is nothing but speed change.

First, we need to know the initial velocity and the force of gravity. So the velocity with friction is found by the formula, initial velocity minus the coefficient of friction times the force of gravity and the time given. v(t) = v₀ – μg t

How to find the coefficient of friction?

The coefficient of friction is the factor that is present between the body under motion and the surface with which it is in motion.

The formula for coefficient of friction is, μ = (frictional force) / (force of normal). Another point to be noted is that the frictional force is sometimes equal to the net force acting on the body, which makes it easier to calculate the acceleration. The normal force is calculated by multiplying the force of gravity and the mass of the body.

What are the different types of friction?

Static and kinetic friction is the two different types that come under one topic of friction.

Static friction is known as friction when a body is not under any motion. It is evident from the word static itself that nothing is in motion. In such cases, the friction found is called static friction. When a body moves away from its equilibrium it is also due to friction and that kind is called as kinetic friction. The static and kinetic friction differs according to the cases, and conditions are given.

Why static friction is called so?

Static friction is called so because it is the force that opposes the body that is not under motion.

When a body does not move and stays in an equilibrium position, the kind of friction acting on the body is called static friction. This friction always acts in the opposite direction to force acting along with the body’s motion even when not in action.

Also Read:

How to Find Acceleration with Friction: Exhaustive Approaches and Facts

January 21, 2024December 14, 2021 by Keerthana Srikumar

Acceleration is a fundamental concept in physics that measures the change in velocity over time. When dealing with objects in motion, it is essential to consider external factors such as friction. Friction is a force that opposes the motion of an object and can significantly impact its acceleration. In this blog post, we will explore how to find acceleration with friction. We will discuss various scenarios and provide formulas and examples to help you understand the calculations involved.

How to Calculate Acceleration with Friction Coefficient and Mass

Explanation of Friction Coefficient and Mass

Friction coefficient, often represented as “μ” (mu), is a value that quantifies the level of friction between two surfaces in contact. It depends on the nature of the surfaces and is dimensionless. The coefficient of friction can take on different values depending on whether the surfaces are at rest or in motion relative to each other.

Mass, on the other hand, refers to the amount of matter an object contains. It is a scalar quantity and is often denoted by “m.” Mass is measured in kilograms (kg) and plays a crucial role in determining the acceleration of an object.

Formula for Calculating Acceleration with Friction Coefficient and Mass

To calculate the acceleration of an object considering friction, we can use the following formula:

$a = frac{F_{net}}{m}$

Where:
– $a$ represents the acceleration of the object
– $F_{net}$ is the net force acting on the object
– $m$ is the mass of the object

Worked Out Example

Let’s consider an example to illustrate how to calculate acceleration with friction coefficient and mass.

Suppose we have a box with a mass of 5 kg. The coefficient of friction between the box and the surface it’s on is 0.2. If a net force of 30 N is applied to the box, what will be its acceleration?

First, we need to calculate the frictional force using the formula:

$F_{friction} = mu cdot F_{normal}$

Here, $F_{normal}$ represents the normal force acting on the box. In this case, $F_{normal}$ is equal to the weight of the box, which is given by:

$F_{normal} = m cdot g$

Where $g$ is the acceleration due to gravity (approximately 9.8 m/s²).

Substituting the values into the formulas, we can calculate the frictional force:

$F_{normal} = 5 cdot 9.8 = 49 , text{N}$
$F_{friction} = 0.2 cdot 49 = 9.8 , text{N}$

Now, let’s find the net force acting on the box:

$F_{net} = F_{applied} - F_{friction} = 30 - 9.8 = 20.2 , text{N}$

Finally, we can calculate the acceleration using the formula:

$a = frac{F_{net}}{m} = frac{20.2}{5} = 4.04 , text{m/s²}$

Therefore, the box will accelerate at a rate of 4.04 m/s² when a net force of 30 N is applied, considering the friction coefficient and mass.

How to Determine Acceleration with Friction and Applied Force

Image by Stannered – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY 2.5.

Explanation of Applied Force

The applied force refers to an external force acting on an object, causing it to accelerate. It can be exerted by pushing, pulling, or any other means. When calculating acceleration with friction and applied force, we need to consider both forces and their effects on the object’s motion.

Formula for Calculating Acceleration with Applied Force and Friction

To determine the acceleration of an object considering both the applied force and friction, we can use the following formula:

$a = frac{F_{applied} - F_{friction}}{m}$

Where:
– $a$ represents the acceleration of the object
– $F_{applied}$ is the force applied to the object
– $F_{friction}$ is the frictional force acting on the object
– $m$ is the mass of the object

Worked Out Example

Let’s consider another example to demonstrate how to determine acceleration with friction and applied force.

Suppose a 10 kg object is subjected to an applied force of 50 N. The frictional force acting on the object is 20 N. What will be the object’s acceleration?

Using the formula mentioned earlier, we can calculate the acceleration:

$a = frac{F_{applied} - F_{friction}}{m} = frac{50 - 20}{10} = 3 , text{m/s²}$

Therefore, the object will accelerate at a rate of 3 m/s² when an applied force of 50 N is acting on it, considering the frictional force and mass.

How to Measure Acceleration with Friction and Angle

Explanation of Angle in Relation to Acceleration and Friction

When dealing with inclined planes or surfaces with an angle, the angle plays a significant role in determining the acceleration of an object. The angle affects the component of the gravitational force parallel to the surface, which in turn affects the frictional force. It is crucial to consider the angle when calculating acceleration with friction.

Formula for Calculating Acceleration with Friction and Angle

To measure the acceleration of an object considering friction and angle, we can use the following formula:

$a = frac{F_{net} - F_{friction}}{m}$

Where:
– $a$ represents the acceleration of the object
– $F_{net}$ is the net force acting on the object
– $F_{friction}$ is the frictional force acting on the object
– $m$ is the mass of the object

Worked Out Example

Let’s explore an example to illustrate how to measure acceleration with friction and angle.

Suppose a block with a mass of 2 kg is placed on an inclined plane with an angle of 30°. The coefficient of friction between the block and the plane is 0.4. If a net force of 10 N is applied parallel to the plane, what will be the block’s acceleration?

First, we need to calculate the frictional force using the formula:

$F_{friction} = mu cdot F_{normal}$

The normal force $(F_{normal}$ ) can be calculated using the formula:

$F_{normal} = m cdot g cdot cos(theta)$

Where $g$ is the acceleration due to gravity $approximately 9.8 m/s²) and (theta$ is the angle.

Substituting the values into the formulas, we can calculate the frictional force:

$F_{normal} = 2 cdot 9.8 cdot cos(30°) approx 16.86 , text{N}$
$F_{friction} = 0.4 cdot 16.86 approx 6.74 , text{N}$

Now, let’s find the net force acting on the block:

$F_{net} = F_{applied} - F_{friction} = 10 - 6.74 approx 3.26 , text{N}$

Finally, we can calculate the acceleration using the formula mentioned earlier:

$a = frac{F_{net} - F_{friction}}{m} = frac{3.26 - 6.74}{2} approx -1.74 , text{m/s²}$

Note that the negative sign indicates that the acceleration is in the opposite direction of the applied force. Therefore, the block will experience a deceleration of approximately 1.74 m/s² when a net force of 10 N is applied parallel to the inclined plane, considering the frictional force, mass, and angle.

How can the concept of friction be used to find acceleration using the coefficient of friction?

The Finding acceleration using coefficient of friction. article discusses how to determine acceleration by utilizing the concept of friction and the coefficient of friction. Friction plays a crucial role in objects’ motion, and the coefficient of friction quantifies the amount of friction present. By understanding how these factors interact, it becomes possible to calculate acceleration. This knowledge is particularly useful in various fields, such as physics, engineering, and mechanics, where understanding and manipulating motion is essential.

Numerical Problems on How to Find Acceleration with Friction

Problem 1:

A block of mass 5 kg is pushed with a force of 20 N on a horizontal surface. The coefficient of friction between the block and the surface is 0.3. Calculate the acceleration of the block.

Solution:

Given:
Mass of the block, m = 5 kg
Force applied, F = 20 N
Coefficient of friction, mu = 0.3

The force of friction can be calculated using the equation:
$f = mu cdot N$

Where N is the normal force, which is equal to the weight of the block:
$N = mg$

The net force acting on the block is given by:
$F_{text{net}} = F - f$

Using Newton’s second law of motion, the acceleration can be calculated using the equation:
$F_{text{net}} = ma$

Substituting the values, we have:
$20 - (0.3 cdot 5 cdot 9.8) = 5a$

Simplifying the equation, we get:
$20 - 14.7 = 5a$
$5.3 = 5a$

Therefore, the acceleration of the block is:
$a = frac{5.3}{5}$

Hence, the acceleration of the block is 1.06 m/s².

Problem 2:

A car of mass 1200 kg is moving with a constant velocity of 15 m/s. The frictional force acting on the car is 400 N. Calculate the coefficient of friction between the car’s tires and the road.

Solution:

Given:
Mass of the car, m = 1200 kg
Velocity of the car, v = 15 m/s
Frictional force, F = 400 N

The force of friction can be calculated using the equation:
$f = mu cdot N$

Since the car is moving with a constant velocity, the net force acting on it is zero:
$F_{text{net}} = 0$

The net force acting on the car can be calculated using the equation:
$F_{text{net}} = F - f$

Substituting the values, we have:
$0 = 400 - mu cdot (1200 cdot 9.8)$

Simplifying the equation, we get:
$0 = 400 - 11760mu$

Solving for $mu$ , we find:
$mu = frac{400}{11760}$

Hence, the coefficient of friction between the car’s tires and the road is approximately 0.034.

Problem 3:

Image by Ysogo – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

A sled of mass 50 kg is moving down a snowy hill with an acceleration of 2.5 m/s². The coefficient of friction between the sled and the snow is 0.2. Calculate the force of friction acting on the sled.

Solution:

Given:
Mass of the sled, m = 50 kg
Acceleration, a = 2.5 m/s²
Coefficient of friction, mu = 0.2

The force of friction can be calculated using the equation:
$f = mu cdot N$

The normal force, N, can be calculated using the equation:
$N = mg$

The net force acting on the sled can be calculated using the equation:
$F_{text{net}} = ma$

Since the sled is moving down the hill, the direction of the net force is opposite to the direction of motion. Therefore, we have:
$F_{text{net}} = -f$

Substituting the values, we get:
$ma = -mu cdot mg$

Simplifying the equation, we find:
$a = -mu cdot g$

Substituting the given values, we have:
$2.5 = -0.2 cdot 9.8$

Hence, the force of friction acting on the sled is:
$f = mu cdot N = 0.2 cdot 50 cdot 9.8$

Also Read:

How to Calculate Acceleration Using Force and Mass: A Comprehensive Guide

June 26, 2024December 7, 2021 by Keerthana Srikumar

how to calculate acceleration with force and mass 1

Calculating acceleration using force and mass is a fundamental concept in classical mechanics, governed by Newton’s second law of motion. This comprehensive guide will walk you through the step-by-step process, provide theoretical explanations, and offer practical examples to help you master this essential skill.

Understanding the Relationship Between Force, Mass, and Acceleration

According to Newton’s second law of motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This relationship can be expressed mathematically as:

F = m × a

Where:
– F is the net force acting on the object, measured in Newtons (N)
– m is the mass of the object, measured in kilograms (kg)
– a is the acceleration of the object, measured in meters per second squared (m/s²)

Rearranging this equation, we can solve for the acceleration:

a = F / m

This formula is the key to calculating acceleration using force and mass.

Step-by-Step Guide to Calculating Acceleration

To calculate the acceleration of an object using force and mass, follow these steps:

Measure the Mass:
Determine the mass of the object in kilograms (kg). This can be done using a scale or a mass measurement device.
Measure the Force:
Measure the net force acting on the object in Newtons (N). This can be done using a force sensor or by applying a known force and measuring its magnitude.
Calculate Acceleration:
Plug the values of force (F) and mass (m) into the formula:
a = F / m
Perform the calculation to find the acceleration (a) in meters per second squared (m/s²).

Example Calculations

Let’s go through some examples to illustrate the process:

Example 1:
Mass (m) = 10 kg
Force (F) = 50 N
Acceleration (a) = F / m = 50 N / 10 kg = 5 m/s²
Example 2:
Mass (m) = 3 kg
Force (F) = 12 N
Acceleration (a) = F / m = 12 N / 3 kg = 4 m/s²
Example 3:
Mass (m) = 16,000 kg
Force (F) = 200,000 N
Acceleration (a) = F / m = 200,000 N / 16,000 kg = 12.5 m/s²

Theoretical Explanation: Newton’s Second Law of Motion

The relationship between force, mass, and acceleration is governed by Newton’s second law of motion, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.

Mathematically, this can be expressed as:

F = m × a

This formula is the foundation for calculating acceleration using force and mass. By rearranging the equation, we can solve for the acceleration:

a = F / m

Key Concepts and Definitions

Mass: The total amount of matter in an object, measured in kilograms (kg).
Force: The push or pull acting on an object, measured in Newtons (N).
Acceleration: The rate of change in velocity, measured in meters per second squared (m/s²).

Figures and Data Points

To further illustrate the concept, let’s consider the following data points:

Mass: 10 kg, 3 kg, 16,000 kg
Force: 50 N, 12 N, 200,000 N
Acceleration: 5 m/s², 4 m/s², 12.5 m/s²

These data points can be used to calculate the acceleration using the formula a = F / m.

Reference Links

By following the step-by-step guide, understanding the theoretical foundations, and applying the provided examples and data points, you should now have a comprehensive understanding of how to calculate acceleration using force and mass. Remember to practice with various scenarios to solidify your knowledge and become proficient in this essential physics skill.

How is Magnetic Field Produced: Detailed Insight And Facts

January 21, 2024December 4, 2021 by Keerthana Srikumar

How is magnetic field produced is one of the important questions that arise. We know that it is the field that influences the electric charges, electric field and the electric current in that system.

It is a universal fact that a magnetic field is produced only when the electric field is present in a system. When an electric current is passed over an element, it instantly creates its electric field only due to its passing.

After the electric field is produced, the magnetic field’s entry is next. Here is the answer to the question of how is magnetic field is produced. So on a wining material when current is passed magnetic field is instantly produced.

Several experiments explain how its magnetic field is produced. And now we take a small example of a solenoid. This element produces a magnetic field when an electric current is produced.

Due to the movement of charges, which creates an electric field. Magnetic field is created due to one of these reasons.

8295846265 751a5f159c — “I’m wandering whether these solar flares will effect this compass? #magnetism #flux #compass #solarflare #instagram #iphoneography” by Podknox is licensed under CC BY 2.0

Magnetic field produced by the solenoid

A solenoid is a thin long wire wound around an element. This thin material will help conduct electric current in the system. An instant electric field is created when the current is passed over it. This, in turn, produces a magnetic field.

A solenoid produces a magnetic field because it uses simple means, unlike the rest. It converts electric current into mechanical, for instance, in a switch.

Inside a switch, a solenoid converts the electric current into mechanical action. Solenoid depends on the magnetic field produced and the number of its turns.

In this kind of element called solenoid it is possible to resolve to reverse the magnetic field that is produced by passing electricity.

solenod — “Solenoid spring mod” by oskay is licensed under CC BY 2.0

Which of the method applied to produce the magnetic field

Fundamentally three different methods produce magnetic fields:

Permanent Magnets
Electromagnets
Earth’s Magnetic Field

Permanent Magnets:

Permanent magnets are magnetized elements using electric current when a material is wound around an element. A permanent magnet is made by striking a ferromagnetic material or two magnets.

For example, two magnets are taken and made to face opposite poles. When the ends of the magnets are beaten to high temperature, it finally becomes a permanent magnet.

The magnetic field in a particular system can also be created by the use of a permanent magnet. This permanent magnet creates a force on other magnets and creates an instant magnetic field.

355133836 f9075e699f b — “Magnets” by steven m is licensed under CC BY 2.0

Electromagnets:

In this type of element an electric current is passed over the element so that it gets magnetized instantly. The conventional current is created when the heat escapes from the system.

Through which the electric field is produced. One of the few reasons for the magnetic field production in an element is due to the presence of electric field.

An advantage to be noted is that an electric field is a cause for the magnetic field to be produced in this electromagnet. The use of the electromagnet can control the magnetic field produced in an element.

At certain times, the permanent magnet creates a good magnetic field. It is also strong enough, but it becomes weak when used in specific materials and requires intense magnetic flux.

At this point, the aid of electromagnet comes into act. The advantage of electromagnet over a permanent magnet is that the magnetic field is created is much stronger. In an electromagnet, electricity is applied to create a stronger magnetic field.

The word electromagnet itself defines an electric current and magnetic field. How is the magnetic field produced, the question most asked, and the above explanation does the justice.

Earth’s Magnetic Field:

This has the strongest fields compared to the other conventional field inside the earth. It is caused by solidifying the liquid iron core of the Earth.

We all know that the magnetic fields are stronger at the poles. It is much stronger when it comes to the Earth’s magnetic field.

Like any other magnetic field, even the Earth’s magnetic field is maintained and controlled. Geodynamo controls and maintains the magnetic field of the earth.

How is magnetic field created in an electromagnet

It is evident from all the studies that an electromagnet is way more convenient than any other magnet to produce a strong magnetic field.

Simple because other magnets produce a magnetic field, but we don’t know. Hence we chose a safer method to produce the magnetic field.

A temporary magnet produces a magnetic field but is weak and of no use. Hence here the use of a permanent magnet comes into act. From which a proper magnetic field is created. The magnetic field is weak, so it can’t be applied to any system.

Hence electromagnet always comes to the rescue of producing a much stronger magnetic field. This type of electricity is employed to create much stronger magnetic flux lines.

Process behind producing a magnetic field using an electromagnet

Firstly we need to be aware of how is an electromagnet made. The process is simple. We must take an element over which a wire is wound around. This wire is called a solenoid.

The solenoid is a simple thin long wire with n number of turns. This material is wound around a conducting element, and when the electric current is passed through it, an instant electric field is produced.

The process behind it is, the electric current is passed over the wound material since it is in circularly wound, and when current is applied, it produces the magnetic flux. The magnetic field lines are in circular mode.

Finally, a magnetic field is produced via a current-conducting material with a solenoid wound.

How are magnetic fields created in planets

The molten liquid generally produces a magnetic field in planets in the core of the planet and the planet’s motion. A magnetic field is easily created since a liquid iron is present in the planet’s core.

Like any other magnets, planets do have poles. These poles are the reason for the attractive and repellant force present.

Like any other magnetic field production by producing electric current, similarly the same on planets too. The electricity in planets is produced when the liquid present at the planet’s core is churned every time.

This electricity created produces a magnetic field on the planet. The magnetic field in the planets acts as an extensive bar magnet. It is also the reason for the rotational axis of the planets.

how is magnetic field produced — “Dynamic Earth – Earth’s Magnetic Field” by NASA Goddard Photo and Video is licensed under CC BY 2.0

Why are magnets always dipoles

It is universal that there is something called north and south, east and west. Our Earth consists of north and south poles, and the horizontal is called the equator and not as east and west.

Likewise, another element that has a north pole and south pole is called as magnet. As far as science is considered, monopole seems not to exist. And a magnet cannot be made without two poles.

Magnets are particularly has as a dipole existence due to the fact that the ends of the magnet have been named as north and south poles respectively. Another point to be remembered is that poles repel and unlike poles attract. From this very fact, there arises a term called a magnetic dipole.

A magnetic dipole is the analogy of an electric dipole in which there are opposite charges at the ends of the electric dipole. The dipole is the reason for a closed-loop in any magnetic system.

How is magnetic field produced on Earth

Earth is the giant magnet of all times. The reason behind it is the magnetic fields produced on the Earth are much stronger than the conventional ones.

On every planet, there is a molten liquid of a particular metal. Likewise, liquid molten iron ore is present in the Earth’s core. This liquid reacts with the motion of the Earth, creating a stronger magnetic field.

The movement of these liquids and churning of them creates strong electricity. This electricity is one of the main reasons for how magnetic field is produced on Earth.

Earth acts as the giant bar magnet to manage the magnetic field by itself. It is also the reason behind the Earth’s rotation from its axis.

Also Read:

Magnetic Force On Moving Charge:7 Facts & Problems Solution

January 20, 2024November 29, 2021 by Keerthana Srikumar

Magnetic Force on moving charge in magnetic field is possible only due to the presence of electric field created by the charges moving from positive end to the negative end.Now let’s see how a magnetic fields are created.

When there is current flowing due to the motion of electric charges produce magnetic fields. When the nucleus of atom orbits continuously then the magnetic force on moving charges in magnetic field is determined.The force on a negative charge is in exactly the opposite direction to that on a positive moving charge.

Fundamentally, when a current is passed over an element electric field is witnessed Here we consider the element to be a solenoid which in turn create magnetic fields in and around the region. This magnetic force exerted on the charge particle will affect any particle entering the field.

It is a known fact that an electric field is produced by static charges and when another charged particle is brought closer it is either attracted or repelled. So in this way, the electric field has a force that will act on the charges present in the electric field.

Similarly, there exists a magnetic force on a moving charge in magnetic fields. Here we will deal with inductors to show how the force on a moving charge in magnetic field is possible. In an electric field, it is capacitors that will be the reason for force on a moving charge.

How charged particle moves in magnetic field

We consider a current filament where electric current flows in a certain direction of the magnetic field is produced in circular form. This filament can also be a solenoid.

At this moment a charge enters the magnetic field region with a certain velocity. Since the magnetic field lines are not similar to the electric field line, they will form a circular path. The charge entering the magnetic field will travel in the circular path as well.

Force on a moving charge on the magnetic field is the process happening basically when a charge passes through the magnetic flux lines. The magnetic fields exert forces by the magnetic flux line on a charge moving within becomes zero if it is parallel to magnetic field lines.

Force on moving charge formula

We are well aware of how the magnetic fields exert forces on a moving charge that comes inside the flux lines. The magnetic field is in right angles to the charge that is undergoing motion.

The magnetic force on moving particle in the magnetic fields is denoted by : F = q V B sineθ.

Lets try to understand the derivation and implementation :

Because the charge does not experience any change in its kinetic energy, since the charged particle moves in a circular motion. So when anything that experiences a circular motion will have zero displacements and the kinetic energy will remain the same.

Considering this we shall determine the formula for magnetic force on a moving charge in magnetic field.

The magnetic flux line or the magnetic fields are denoted by the letter B, the charge that enters and moves inside the magnetic field is denoted by the letter q. The velocity with which the charge moves inside the magnetic field is denoted by the letter V.

When the charge moves inside the magnetic field, the field exert forces on the charge. This magnetic force is related to certain parameters. The parameter for the force magnitude is as explained; it is proportional to the magnitude of the charge, the magnitude of the velocity of the charge under motion, and the magnetic field.

The exert forces by magnetic field proportional to sine θ. Meaning, θ is the angle made by the velocity of the charge that moves with the magnetic flux lines.

Force on moving charge formula (Explanations):

Now the formula for magnetic force on moving charge is F = q V B sineθ.

As in the case of force it is basically a vector quantity having magnitude and direction. The formula mentioned previously is used to calculate magnitude of the force. The direction of the magnetic force is the direction of the charge moving in the magnetic field.

The direction of the magnetic charge travelling inside the magnetic field is in right angles to both the velocity and the magnetic field. The formula for this condition is F = q V B sine θ an.

Therefore when the motion of the charge is right angles to the velocity and the magnetic field the formula is revised and given as F = q (V X B). Because θ becomes 90⁰ and sine 90⁰ is equal to one.

Hence the formula for the magnetic force on moving charge in the magnetic field is given by three different conditions and can be used according to the problems provided.

Moving charge in a uniform magnetic field derivation

A Uniform magnetic field is produced when a current-carrying solenoid is passed with an electric current. This is easily explained using Right Hand Thumb Rule or also called as Lorentz Force.

The above mentioned formula is used to calculate the magnetic force employed on the charge moving inside the magnetic field.

The right-hand thumb rule is defined as; the thumb indicating the direction of velocity, the index finger indicating the direction of the magnetic field (B), and the middle finger indicating the direction of the resultant force.

The right-hand thumb rule is also known as Lorentz Force. The formula of Lorentz Force is F = q V B sine θ. Here q is the charge in the magnetic field, V is the velocity, B is the magnetic field and θ is the angle made between velocity and magnetic field.

Zero force on moving charge:

It is now a known fact that the charge moving inside the magnetic field will undergo a circular motion. The force acting on this will have a different result compared to the conventional one.

When electric current is present in a solenoid, eventually a magnetic is created. The flux lines are in a circular motion that is they are produced around the solenoid.

Hence when a charge moves inside the region of the magnetic field they follow the direction of the magnetic flux lines. A circular motion is eventually created inside. The charge will move in the same direction and then have no change in the kinetic energy.

Since there is no displacement in the whole system the force is said to be zero. The reason is that the charge will go on and on moving in circles in the direction of the magnetic flux lines.

The velocity with which the charge moves inside the magnetic field is parallel to the magnetic field. So the magnetic force on moving charge will be eventually zero.

A charge moving equally parallel in the same direction of the magnetic field, then magnetic force acting that particular magnetic field is zero.

In essence of the work done on the charge in a magnetic field is zero or minimum. In a magnetic field if the kinetic energy of the charge is said be zero the the system obeys work-energy theorem.

Here in this case when the magnetic force becomes perpendicular to the velocity the direction might not change but the magnitude will change. So the word done on the charge will be zero, making the force acting on the charge also zero.

Direction of moving charge in magnetic field:

The magnetic field direction created by a moving charge is perpendicular to the direction of motion of the charged particle. Hence the magnetic force generated due to a magnetic field is perpendicular to the direction of motion of the movement and speed of the charged particle.

Problems and solutions:

Problem 1: Consider a charge to move in the north direction with a speed of 3 x 106 m/s. a magnitude of 4.0T will act in the west direction. Now calculate the magnitude of the force on moving charge in the magnetic field? [The charge moving inside the magnetic field is the proton].

magnetic force on moving charge in magnetic field

Solution:

Let us consider the right-hand thumb rule. The force coming out of the hand is the magnetic force on moving charge.

Magnitude of the force is F = q V B sineθ

F = (1.6 x 10-19C x 3 x 106 x 4 T x sine 90⁰)

F = 1.92 x 10-12 N

Problem 2: Calculates the earth’s magnetic field when the positive moving charge in the system has a velocity 2 x 105m/s moving in the north direction and the magnitude of the force acting on it is 1.2 x 10-13N in the west direction.

Solution:

Formula is F = q V B sine θ

B = F / (q x V x sine θ)

B = (1.2 x 10-13) / (2 x 105 x 1.6 x 10-19 x sine 90⁰)

B = 3.75 T

Therefore now it is clear that the magnetic force on moving charge has different conditions from the explanation and the formulae.

Also Read:

Force On Moving Charge In Electric Field: Several Approaches and Problem Examples

January 21, 2024November 25, 2021 by Keerthana Srikumar

Force on moving charge in electric field is determined when a charged particle moves without acceleration it produces an electric field.

Firstly an electric field is created when two parallel plates are charged, otherwise called capacitors. When the test charges are placed between the charged capacitor plates they move from the positive end to the negative end. Each such charge carries like this creating a line.

The test charges move from positive to negative side creating lines of force is called an electric field. Since these lines of charges form a uniform pattern, then there is said to be a uniform electric field created.

Force On Moving Charge In Electric Field

When a test charge is placed on the negative side of the plate, it will attract, and the force of attraction will be less. But when another test charge is placed closer to the positive side of the plate opposite to that of the other plate, the force of attraction would be more.

When the test charge is placed closer to the positive side of the charge, the repulsion is greater, and the force of attraction to the negative side of the plate is greater. So the force on a moving charge in an electric field depends on where the charge is situated and the distance.

Electric field is created only when the charges are at stationary. Therefore the force on that charge is determined based on the position of the test charge. Whether it is closer or far from the respective charges, it is placed.

How do you calculate the force of a moving charge

Force on moving charge in electric field is calculated using the formula is F = e E, here we consider the charge as electron and it is denoted by letter e. The electric field is denoted by letter E.

The force of the electron is nothing but the acceleration all over the mass of the electron in an electric field, and it is given as a = (e E) / m. This formula defines the electric field as the force by unit charge, E = F / q (e).

Now acceleration has been calculated, and the velocity goes like this, V_f² = V₀² + 2 a ∆ X. Where Vf is final velocity, and V0 is the initial velocity. The above formula is given in the assumption that the electron does not gain speed. This speed should not get too nearest to the light speed (3 X 10⁸ m/s), or else it would become a whole different scenario. Hence the speed of the charge must be below.

From the above picture, consider a negative test charge moving across electric fields. This charge has an initial velocity, and it will shoot up the electric field and not pass through it since two parallel plates have negative and positive charges on opposite sides.

When an electron with a negative charge is placed between the plates, it gets deflected by the charges present in the vicinity. Since the uniform electric field is produced in the process, the charge travels faster with the initial velocity and is also perpendicular to the field.

The charge experiencing a force when deflected by the electric field it will give a projectile. The electron will displace from its original place (x) to a new position called y. This forms a projectile path.

Now there are possibilities for the charge to move out of the plates. When this happens, it makes an angle θ with a projectile path. Here we must know what (y) is and θ is. The deflection comes from the image, (y), and θ is the electron’s angle emerges out of the plates.

The electron placed between the plates experiences a force upwards because the side of the plate facing inward has a positive charge. Hence the electron will be attracted towards that side of the plate.

We need to calculate the force, acceleration, and velocity of the charge moving in the electric field. The force experienced by the moving charge in an electric field at point (y) is F_y = eE. Acceleration is a_y = (eE) / m.

The deflection (y) is formulated, and finally, we get the equation to calcite the force is as follows (y) = (eE x2) / 2my2. Then the angle at which the electron emerges out of the charged capacitor plates is as given, tan θ = (eEx) / mV₀² .

This is the basic formula we need to know before calculating the force on moving charges in the electric field. So, for now, we deal with simple techniques and so on.

Force on moving charge in electric field is the charge multiplied by the electric field or uniform electric field.

Force on a moving charge in a uniform electric field

We need to know that when a charge is in motion, it produces only a magnetic field. The charges which are not in motion produce electricity by default. Presence of an electric field causes magnetic field to be produced.

In a system, a point charge and a test charge is present. So the force exerted by the point charge on the test charge is called the electrostatic force. This is the force present on the moving charge in an electric field.

We can clearly understand how a force acts on a moving charge in an electric field using an example.

A charge travelling between the capacitor plates is attracted and repelled silmultaneously. When two plates are placed at a distance d the plates facing each other will have opposite charges.

So when a test charge is placed between, it will either get attracted or repelled depending on the magnitude it possesses.

Problems examples on Force On Moving Charge In Electric Field

From the above-shown diagram, we must determine the sign or charge of the particle moving in a projectile motion. We know that 1, 2 travel in one direction and 3 travel in another direction.

Positively charged plate is placed on top, and the negatively charged plate below. Both the plates are faced inwards. And the charges are inwards.

Now the charges 1 and 2 travel towards the positive side of the plate, and charge 3 travel towards the negative side of the plate.

Charges 1 and 2 are negatively charged, and charge 3 is positively charged. This is a very simple way to find the sign of the charge moving in the electric field experiencing a force.

We will have to determine the charge to mass ratio, whether high or low, based on the direction in which each of these charges travels.

Charge 3 will have a charge-to-mass ratio very high due to the deflection being high. Meaning, that charge three is deflected to a long position from its original position. Since the deflection is high, the charge to mass ratio is also high.

Consider two charged plates kept parallel to each other in a horizontal manner. Positively charged and negatively charged plates are placed top and bottom respectively. Length of the plate is l and the distance between the two plates is given by d

A charge mass m and charge +q are placed between the plates. This +q charge will be attracted to the lower plate. The electron has an initial velocity of V0. This velocity determines how far the charge will travel due to the presence of an electric field.

So now we need to find the minimum amount of initial velocity required to deflect more and just emerge out of the plates.

We know that the force is F_y = eE and acceleration is a_y= (qE) / m. Using this information, a tedious calculation is made, and finally, we get the equation for calculating the minimum initial velocity. And that will be V₀ = L {(qE / MD)}^1/2.

Problem on force on a moving charge in a uniform electric field

Let us consider a charge moving in an electric field. The charge is placed between the charged capacitors. A force acts on the charge while in its motion. The electric field acting on a point charge q= 2 NC is E= 7.91 X 105 N/C. What force does the electric field exert on the charge?

F= eE

F = 2 X 10-9C X 7.19 X 105

F= 0.180N

Now we have a clear understanding of force acting on a moving charge in an electric field.

*************************

Also Read:

Types Of Harmonic Oscillator: Exhaustive Insights and Facts

January 21, 2024November 23, 2021 by Keerthana Srikumar

Types of harmonic oscillator are categorized into several types based on their function ability having a back and forth motion which is usually displaced from its equilibrium position that experiences a restoring force.

Types of harmonic oscillator are as mentioned below:

Simple Harmonic Oscillator
Damped Harmonic Oscillator
Quantum Harmonic Oscillator

Simple Harmonic Oscillator

A simple harmonic oscillator is one of the types of harmonic oscillator. The back and forth periodic motion from the equilibrium position is also known as simple harmonic motion.

The motion experienced by a system in simple harmonic oscillator is periodic. For example, we consider a pendulum that is suspended from the equilibrium position moves back and forth before coming to rest. The motion back and forth decreases with a decrease in amplitude.

In this type of simple harmonic motion, the restoring force is and the magnitude with how much the body experiences motion is proportional to each other when supplanted from its equilibrium position. The restoring force acting upon the object is simply the force used to stop the vibration.

Examples to better understand simple harmonic oscillators

Oscillating Pendulum: A pendulum is a mass suspended from a fixed, rigid support. When a push is given, the system experiences a vibration back and forth from its equilibrium position. This oscillation is periodic and goes by simple harmonic motion.

When a restoring force acts on the oscillations, it decreases as the amplitude decreases and ceases. This oscillation is known as simple harmonic motion.

Types of harmonic oscillator — “Pendulum / giant pocket watch – The Minories” by ell brown is licensed under CC BY 2.0

Another example of the simple harmonic motion is the park swing that we notice in parks. These swings remain at rest until and force acts on them to start the movement. When a person sits on it and starts to swing, it starts the motion.

Swings, when given a slight push, displace from their equilibrium position and move back and forth. This motion is periodic, and also simple harmonic oscillations occur.

14182557265 24358cd6f0 b — “Swings” by halfrain is licensed under CC BY-SA 2.0

Damped Harmonic Oscillator

Damping is the restriction of vibrations and oscillations in an equilibrium system by dissipation of energy. Damping oscillators are the ones in which vibrations decrease with time.

In a damping harmonic circuit, oscillations go on over a long period until and unless a restoring force is acted upon the equilibrium system. This restoring force is one of the reasons for the oscillation’s decay over time.

Damping harmonic oscillators are sub-divided into three types according to its damping factor. The system is said to be critical damping when the damping factor is equal to one. When the damping factor is more than one, it is called overdamped or high damping. The system is said to be underdapmed if the damping factor is less than one.

The damping formula is connected to the Newton Second Law, and according to it, the formula goes like this for any damped harmonic oscillator.

C2 – 4mk = overdamped

C2 – 4mk = critically damped

C2 – 4mk = underdamped

The damping factor for a damping harmonic oscillator is that the vibrations return to zero at the shortest time interval. The system undergoes a harmonic motion; when a restoring force is applied, the oscillations eventually come to rest or back to the equilibrium position in less time interval.

The damped harmonic oscillation is one of the types of harmonic oscillator. An excellent example of damped oscillations is the weight suspended by spring. When the weight is suspended, it displaces from the equilibrium position back and forth and comes to rest eventually.

Harmonic oscillations are the reason for some systems to function with proper back and forth movements. We often tend not to notice the daily events occurring, but we see the harmonic oscillations in them.

Quantum Harmonic Oscillator

Quantum harmonic oscillator is analogical to conventional oscillators. Quantum harmonic oscillator is generally dealt with quantum mechanics. The built-in configuration of a quantum harmonic oscillator is different from the classical harmonic oscillator.

Since the built-in difference for both quantum harmonic oscillator and classic harmonic oscillator, there will be changes in the functionality of any system that comes under any of these oscillators.

Quantum harmonic oscillator models the vibrations in micro-level systems. For example, in quantum optics the representation of the behaviour of vibrations in molecules or molecular levels, wave packets is possible with quantum harmonic oscillators.

In this quantum harmonic oscillator the energy level is said to be evenly spaced without being a continuous one.

Differences in Quantum Harmonic Oscillator

The motion in the quantum harmonic oscillator is similar to the motion in classical harmonic oscillators with few differences. The oscillation or vibration in quantum harmonic oscillator is explained better using Schrodinger’s equation.

Since the built-in difference for both quantum harmonic oscillator and classic harmonic oscillator, there will be changes in the functionality of any system that comes under any of these oscillators.

In this quantum harmonic oscillator the energy level is said to be evenly spaced without being a continuous one.

Frequently Asked Questions

What is the use of harmonic oscillators?

Harmonic oscillators are used in a system to decay the oscillations in a system.

The harmonic oscillators in a system are periodic, and it decreases with the decrease in amplitude. The back and forth motion in a system goes on for a long time until a restoring force is applied to the system.

Why do we use a harmonic oscillator?

A harmonic oscillator is used so that the system comes to the equilibrium position in a concise span.

When the system is undergoing a motion, it will come to rest when a force is applied, and that force is known as restoring force. The oscillations in the system will come to rest or the equilibrium position with decreasing amplitude.

Mention the difference between simple harmonic motion and oscillations?

Simple harmonic motion is period, but oscillations vary.

In simple harmonic motion, the restoring force acting upon the system is not been mentioned. In oscillations, the force which helps decay the oscillations called as restoring force is generally not mentioned.

How is harmonic motion explained?

Harmonic motion is a periodic motion and is explained using a sine wave.

The oscillations of a vibrating system decay with decrease in amplitude. The oscillations undergo some change that is, they will face a restoring force or negative force. This force acts opposite to the motion in which system acts.

Hence, the restoring force and displacement of an oscillating body form the equilibrium position are proportional. One of the types of harmonic oscillator which is the damped harmonic oscillator and this is explained using Newton Second Law.

What is an electric oscillator?

An electric oscillator is the ones that produces electric signals in a circuit in which it is been fabricated and these signals are usually sine wave or square wave.

An excellent example of an electric oscillator is harmonic motion. This electric oscillator converts direct current into alternating current. It produces continuous waveforms without any input. Simple harmonic motion is one of the great examples of harmonic oscillations.

***********************

Also Read:

7 Harmonic Oscillator Examples:Exhaustive Insights and Facts

January 20, 2024November 17, 2021 by Keerthana Srikumar

Harmonic oscillator examples include even mechanical examples; some include electrical examples and system which executes simple harmonic motion.

Mentioned furthermore are a few harmonic oscillator examples:

Pendulum
Subwoofer
RLC Circuit
Mass-Spring System
Bungee Jumping
Cradle
Auditory Perception

Pendulum

The pendulum is a weight suspended from the point of axis for its free flow swinging sideways. When this pendulum is supplanted from its equilibrium position, it starts to oscillate sideways back and forth. The oscillation is regular and is in simple harmonic motion.

Any system that acts in simple harmonic motion comes under a harmonic oscillator. A simple harmonic oscillator is a type of harmonic oscillator. A system is said to be under simple harmonic oscillation when the restoring force is proportional to the displacement.

In a pendulum, the restoring force plays a vital role. The pendulum is sometimes called a pendulum bob. Now when the bob is displaced from its equilibrium position, it swings back and forth harmonically.

Restoring force acts on the pendulum so that the pendulum bob’s swing decreases slowly and the amplitude decreases. Another significant point to remember is that Hook’s Law attributes to this oscillation of the pendulum.

harmonic oscillator examples — “File:Foucault pendulum animated.gif” by DemonDeLuxe (Dominique Toussaint) is licensed under CC BY-SA 3.0

Subwoofer

A subwoofer is a device created to produce low pitch frequency. It has audio frequencies that are low based. The membrane in a subwoofer is said to make harmonic oscillations when the subwoofer delivers low audio frequency.

The subwoofer is a device that comes under a driven oscillator. The membrane in a subwoofer oscillates with constant amplitude producing a harmonic oscillation in the process. So this is an excellent harmonic oscillator example.

Inside a subwoofer is present a driver’s cone, which vibrates when it amplifies electric current into sound. This sound is nothing but the result of the back and forth harmonic oscillation. And the sound is the low base frequency with a low pitch.

We know the setup of a subwoofer and how it works, but we also need to know the presence of a driver’s cone. The driver’s cone is the mechanical part of any speaker system. This converts electrical energy into sound by creating an air space within. And this gives harmonic oscillations.

RLC Circuit

In an RLC circuit introduction of a resistor gives the harmonic oscillation as the LC combination does. This resistor reduces the oscillations in the circuit, therefore, producing low base frequency and decreasing the peak resonant frequency.

The resistor added in an RLC circuit reduces the harmonic oscillations. And this is known as damping. Damping is the one that reduces the oscillations, letting it decay. So for an RLC circuit to act appropriately as a harmonic oscillator, the resistor should be added in parallel and series.

So, in parallel resistor should be added in such a way so that the oscillations do not decay. And in series resistor must be added in small so that the resistance in the circuits is made as small as possible, so the damping doesn’t affect the oscillations.

By changing the resistance according to or equivalently by deciding the damping factor by changing the resistance in a circuit, issues such as dielectric loss in coils and capacitors can be brought up and solved.

Basically, in an RLC oscillator, two types of oscillators come into play, the mechanical oscillator, and the electrical oscillator. One of the main features of the RLC circuit is that it decays even during oscillations. The driven oscillator provides a sinusoidal signal through harmonic oscillations resulting in a sine wave instead of a square wave.

Mass-Spring System

A mass-spring is the system where two more masses are suspended from a rigid support. And the oscillations of the mass from its equilibrium position back and forth are evaluated.

For example, let us consider two springs having two masses, each suspended from the rigid support. The spring constant for both springs would be the same, but the mass may differ. When a mass weighing lighter than the other mass weighs more is suspended, the period of oscillations varies.

Smaller mass will oscillate harmonically less than the mass that is larger than the less suspended mass. The configuration of the masses can be explained by the general coordinates of the two systems.

This is done by considering how far the systems oscillate from their equilibrium position back and forth, finally coming to rest due to the restoring force acting upon them naturally.

The mass-spring system is generally used in equipment where the vibrating part is set apart from the supporting element. For example, in a lightweight roof system, this mass-spring concept is put in to separate it from any loud equipment that is under high vibrations.

mass spring faster — “File:Animated-mass-spring-faster.gif” by Svjo is licensed under CC BY-SA 3.0

Bungee Jumping

Bungee jumping is an excellent harmonic oscillation example. Also, this exhibits the simple harmonic oscillations in a better way. The up and down oscillations of the bungee cord from its equilibrium position explains clearly the simple harmonic oscillations present in the system.

The basic concept of harmonic oscillation in bungee jumping is that the oscillation occurs after the free fall of the jumper. The jumper is tied to the bungee cord, which moves up and down from the equilibrium position. The weight to be suspended in the cord is in accordance with the length of the cord. In this way, Hooke’s Law (F=kx) is obeyed.

The jumper experiences a free-fall, after which harmonic oscillation comes to action. The jumper moves up and down, which happens when the bungee cord oscillates to and forth from the equilibrium position.

Cradle

Cradle exhibits the simple harmonic motion in play. A single push given to the cradle makes it oscillate to and fro from its equilibrium position.

When the cradle is given even a slight push, it oscillates from equilibrium position back and forth. And this comes to rest when the oscillations decrease, making the amplitude smaller. The to and fro motion is period and is said to have simple harmonic oscillations.

Auditory Perception

Auditory perception is also known as the sense of hearing in human beings. This process is carried out when sound waves enter the eardrum causing the vibrations to and fro, and finally, the sound is heard by our human ear.

The sound waves travel through the membrane of the ear canal, oscillating back and forth in periodic motion. This is called simple harmonic motion (oscillation). Both the eardrums oscillate back and forth for four cycles and are associated with the movement of the eyes.

human ear — “Ear” by naikalieva is licensed under CC BY-SA 2.0

These above mentioned examples help us understand the concept of harmonic oscillations in a better way.

Also Read:

Critical Damping Applications:Detailed insights

January 21, 2024November 10, 2021 by Keerthana Srikumar

Critical damping applications are one of the primary forms of bringing an oscillating system to rest. Essential plates of damping are used to get the vibrations of the system to complete rest.

Given below are a few critical damping applications that are found in daily life. Critical damping are very useful for such daily-life activities.

Friction Damping Plates
Electric Circuit Damping
Hydraulic Recoil Machine
Door-closing Mechanism
Speedometer
Automobile Shock Absorber

Friction Damping Plates

Friction damping plates are the devices that reduce the excessive vibrations in a system, thus converting kinetic energy into thermal energy through friction. The concept of critical damping comes into action here.

This brings the massive vibrations to the equilibrium position as quickly as possible. Therefore the friction damping plates are primarily used in building to dissipate seismic energy by which the building can withstand an earthquake.

The concept is, when a building encounters an earthquake, the plates underground change places but the friction damping plates make sure plates under the construction come back to the rest position, causing less destruction. In this way, critical damping applications find their uses.

Electric Circuit Damping

A primary RLC circuit is known as an electrical circuit. R means resistor, L means inductor, and C implies capacitor.

In this circuit, an inductor (L) stores the energy in a magnetic field when the electric current flows through the circuit; a capacitor (C) stores electric charges, which is why the electric current passes. But a resistor (R) breaks the current flow in a system similar to the damping in oscillating systems.

Here the addition of a resistor in an electric circuit decays the oscillations of the circuit when connected in parallel.

The resistor reduces the peak resonant frequency in the circuit. Critical damping is one of the primary reasons for reducing frequency due to the arising from the LC combination in the RLC circuit.

Hydraulic Recoil Mechanism

When a firearm fitted with hydraulic recoil, it reduces the effects of recoil in the gun and provides accuracy. The hydraulic recoil fixed in the barrel, so when the gun is fired, the recoil energy caused by the projectile makes the barrel go backward and locked in the bolt.

Basically, a barrel and the bold are together, soon after firing next step is that the barrel and bold travel backward till the end of the gun and come forward with some force so that the bold is firm, filling the next cartridge. In contrast, the barrel goes forwards and pushes the current cartridge to be fired.

This phenomenon occurs because the critical damping is present; this helps the barrel return to the rest position as quickly as possible to fire the next one.

Door-closing Mechanism

Adding a door damper (critically damped) reduces the damage to the door system as a whole.

Generally, when a door opens and closes, it makes noise, and damage occurs to the doorframe and such. So when a damper attaches to the door, it reduces the door from slamming and causing destruction.

Once the door opens, it suddenly comes back to its original position with no further delay and also has no adverse effect on the system. Critical damping helps the system from further damage or so.

Speedometer

Speedometers are critically damped instruments so that when the vehicle accelerates, it does not oscillate and create disturbances during riding or driving.

In the speedometer, the needle that indicates the speed does not constantly oscillate and confuses the person handling the vehicle.

Since the speedometer is critically damped, it does not have a constant oscillation; once the vehicle is accelerated, it does not oscillate at all and stays in that stable position unless the velocity is changed, which changes the acceleration.

Automobile Shock Absorber

Shock absorbers are a spring present in cars that dissipate the energy created from an abrupt movement while the car goes through a rough patch. This spring smoothens the entire ride of the vehicle.

The spring, also called a shock absorber, absorbs part of the abrupt movement in the form of energy during the ride, which dissipates the energy.

As this is a continuous process, the spring has to do this as quickly as possible, so the car goes up and down. The shock absorber returns to its original place and controls the process as well.

What is critical damping resistance

Critical damping resistance is the resistance of a critically damped electric circuit and ceases the oscillations.

An RLC circuit is the best suited to determine the resistance of a critically damped circuit. R is the resistor, L is the inductor, and C is the capacitor. The LC combination is the reason behind the oscillations of the system. R-value affects the damping of the whole system.

When R is small or large, it means the circuit is either underdamped or overdamped. When the circuit is underdamped, ringing happens that is the function of the circuit occurs. Here it is ringing, but in the other circuits, it can be ringing and any other application.

When R is made small, it reduces the frequency due to the oscillation in the system. Resistance is the one that breaks the flow of electric current, hence in a circuit, the resistance and cuts down the peaks of the resonant frequency.

The critical damping resistance can also be explained as the required resistance to stop the oscillations and bring them back to the equilibrium position.

How to find critical damping resistance

Critical damping resistance is calculated using the damping factor. This formula is used to find the critical damping resistance.

For a critically damped circuit(R LC in parallel), the resistance can be found using the formula: ζ = R/2 (C/L)^1/2. Zeta (ζ) is the damping factor and for critical damping (ζ) is 1.

Let us understand using a numerical problem. Calculate the critical damping resistance in the given circuit.

ζ = R/2 (C/L)^1/2

1= R/2 (64/16)^1/2

1= R/2 x 4

R = 0.5 Ω

Critical damping condition

The condition for the critical damping is that the damping factor should be equal to 1. That is Zeta (ζ) = 1.

In a system, the oscillations will completely decay; that is, it will stop and come back to the rest state, the equilibrium position, called critical damping.

The minimum amount of force or resistance (based on which system we are working on) required to stop the system under motion to bring it back to the equilibrium system is critical damping.

The condition for a critically damped system directly depends on the damping factor. And the requirement for critical damping is that the damping factor should always be equal to 1.

The one primary condition for critical damping is that the oscillations must come to a stop without going back and forth and returning to the equilibrium position as quickly as possible.

Why Is Critical Damping Faster Than Overdamped:Detailed Insights

January 21, 2024November 8, 2021 by Keerthana Srikumar

The reason why is critical damping faster than overdamped is because of the fact that critical damping moves to equilibrium state than the overdamping.

Critical damping is applying a resistive force against the oscillating system to bring it to stop it at once. Damping is when a strong resistive force is applied against the motion of an object that is undergoing simple harmonic motion.

Explaining why critical damping is faster than overdamping. A girl on swing will be swinging forever if there wasn’t any air resistance force. But a force must be applied to bring the swing to rest that is when displacement is zero. When displacement is zero, the system is said to be in equilibrium.

When a force is applied to the motion, that is damping applied, the swing moves in a way that the amplitude lowers slowly. This is called as light damping. When a strong force is applied against the motion then the swing is slowed down and the amplitude lowers further more.

Now when there is an even stronger force applied on the swing, it goes past the point of equilibrium and comes back. The force acts negative here and finally the swing comes to rest as quickly as possible making the displacement zero. This is known as critical damping.

Why critical damping is faster than overdamped and this is the reason behind it. At critical damping the oscillating system moves to equilibrium as soon as possible than overdamping.

Why is critical damping faster than overdamped

In an oscillation system, overdamping means the oscillations come to rest after a long time after applying the resistive force. Light damping means the oscillation come to rest gradually. But critical damping means the oscillations come to rest immediately.

A damping system becomes critically damped when the damping factor is (ζ = 1). As the zeta (ζ) value goes more than 1 the system response will become slow and the vibrations or oscillations will take a longer time to reach the equilibrium position.

When ζ values goes lower than 1 the oscillation will gradually come to rest that is it will return to the equilibrium position at a slow pace.

When,

(ζ) = 1; critical damping

(ζ) = >1; overdamping

(ζ) = <1 ; underdamping.

From the above cases we can come to a conclusion that, critical damping is the threshold point above which the overdamping occurs that is equilibrium position attained at a very slow rate. And below which it is known as underdamping that is when the equilibrium position is reached gradually.

So from the observation it is known that critical damping means the return to the equilibrium position of an object under motion is faster than the overdamping.

Frequently Asked Questions

What does critical damping mean?

Critical damping is the threshold point between the overdamping and the underdamping.

For critical damping, the damping factor is equal to 1. When the damping factor goes more than one it is known as overdamping. And when the damping factor goes below 1 it is known as the underdamping.

Which system is considered to be critically damped system?

A system which has the smallest value of amplitude is known as the critically damped system.

The smallest value of amplitude also means that the oscillation or the vibrations of a system is the zero having no value. The system reaches equilibrium position at faster rate. This value separates the non-oscillations from the oscillation.

Why does overdamped take a longer time?

The overdamped takes a long time because it reaches the equilibrium position after a very long time.

Since the damping factor in an overdamped system is more than 1 the system takes a long time to respond and also to reach a steady-state position. The amplitude in this system reduces slowly. This is exactly why critical damping is faster than overdamped.

What is an example of critical damped situation?

Automobile shock absorber is a very good example of critically damped situation.

Critical damping means putting a stop to the vibrations or oscillations to a system under motion. This shock absorber is a device in an automobile which has a control over the mounted device that is in the form of spring mounted.

How is overdamped, underdamped and critically damped system distinguished?

The damping factor the return of the system to the equilibrium position distinguishes the system if it is overdamped, underdamped or critically damped.

When a system returns to the equilibrium position at once with zero vibrations or oscillations it is known as critical damping. Here the damping factor is 1.When a system takes a very long tome time to reach the equilibrium position it is known as overdamped. The damping factor is more than 1. When a system gradually comes back to the equilibrium position it is known as underdamped. The damping factor is less than 1.

***********************

Also Read: