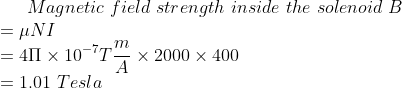Summary
Determining the magnetic field of a solenoid is a fundamental concept in electromagnetism. By understanding the formula B = μ₀ * n * I, where B is the magnetic field, μ₀ is the permeability of free space, n is the number of turns per unit length, and I is the current flowing through the solenoid, you can accurately calculate the magnetic field inside a solenoid. This guide will provide a comprehensive, step-by-step approach to finding the magnetic field of a solenoid, including theoretical explanations, practical examples, and numerical problems to help you master this important topic.
Understanding the Solenoid and its Magnetic Field

A solenoid is a cylindrical coil of wire that, when carrying an electric current, produces a uniform magnetic field inside the coil. The magnetic field lines inside the solenoid are parallel to the axis of the coil, and the field strength is constant throughout the interior of the solenoid.
The formula for the magnetic field strength (B) inside a solenoid is:
B = μ₀ * n * I
Where:
– B is the magnetic field strength, measured in Teslas (T)
– μ₀ is the permeability of free space, which is a constant equal to 4π x 10^-7 T m/A
– n is the number of turns per unit length, measured in turns/meter (m^-1)
– I is the current flowing through the solenoid, measured in Amperes (A)
This formula is derived from the Biot-Savart law, which describes the magnetic field produced by a current-carrying wire. By considering the cumulative effect of all the current-carrying loops in a solenoid, we can arrive at this simplified expression for the magnetic field.
Factors Affecting the Magnetic Field of a Solenoid
The magnetic field of a solenoid is influenced by several key factors:
-
Number of Turns (N): Increasing the number of turns in the solenoid will increase the magnetic field strength, as more current-carrying loops contribute to the overall field.
-
Current (I): Increasing the current flowing through the solenoid will directly increase the magnetic field strength, as per the formula.
-
Length of the Solenoid (L): The length of the solenoid affects the number of turns per unit length (n = N/L). Longer solenoids with the same number of turns will have a lower n, and thus a weaker magnetic field.
-
Diameter of the Solenoid: The diameter of the solenoid does not directly affect the magnetic field strength inside the solenoid, but it can influence the overall field distribution and the magnetic field outside the solenoid.
-
Core Material: Inserting a ferromagnetic material (such as iron) inside the solenoid can significantly increase the magnetic field strength, as the core material will concentrate and amplify the magnetic field.
By understanding how these factors influence the magnetic field, you can design and optimize solenoids for various applications, such as electromagnets, particle accelerators, and magnetic resonance imaging (MRI) systems.
Measuring the Magnetic Field of a Solenoid
To measure the magnetic field of a solenoid, you can use a magnetic field probe or a gaussmeter. The probe should be positioned at the center of the solenoid, along its axis. This ensures that the probe measures the uniform magnetic field inside the solenoid, which is parallel to the axis.
When measuring the magnetic field, it’s important to consider the following:
-
Background Magnetic Field: The magnetic field measured by the probe will include both the field generated by the solenoid and any background magnetic field present in the environment. To isolate the magnetic field due to the solenoid, you should measure the background field with the current turned off and subtract it from the total field measurement.
-
Probe Orientation: The magnetic field probe should be oriented to measure the component of the magnetic field that is parallel to the axis of the solenoid. This is typically the strongest and most uniform component of the field.
-
Probe Positioning: The probe should be positioned at the center of the solenoid, along its axis, to measure the maximum and most uniform magnetic field. Measurements taken closer to the ends of the solenoid may be affected by edge effects and non-uniform field distribution.
-
Multiple Measurements: It’s recommended to take multiple measurements at different points along the solenoid’s axis to ensure consistency and accuracy. Averaging the results can help reduce the impact of any local variations in the magnetic field.
By following these guidelines, you can obtain reliable and accurate measurements of the magnetic field produced by a solenoid.
Calculating the Magnetic Field of a Solenoid
To calculate the magnetic field of a solenoid, you can use the formula:
B = μ₀ * n * I
Where:
– B is the magnetic field strength, measured in Teslas (T)
– μ₀ is the permeability of free space, which is a constant equal to 4π x 10^-7 T m/A
– n is the number of turns per unit length, measured in turns/meter (m^-1)
– I is the current flowing through the solenoid, measured in Amperes (A)
Let’s go through some examples to illustrate the use of this formula:
Example 1:
A solenoid has 500 turns and a length of 20 cm (0.2 m). If the current flowing through the solenoid is 2 A, what is the magnetic field strength inside the solenoid?
Given:
– Number of turns (N) = 500
– Length of the solenoid (L) = 0.2 m
– Current (I) = 2 A
Step 1: Calculate the number of turns per unit length (n)
n = N / L = 500 / 0.2 = 2500 turns/m
Step 2: Calculate the magnetic field strength (B)
B = μ₀ * n * I
B = (4π × 10^-7 T m/A) * (2500 turns/m) * (2 A)
B = 6.28 × 10^-3 T = 6.28 mT
Therefore, the magnetic field strength inside the solenoid is 6.28 mT.
Example 2:
A solenoid has 1000 turns and a length of 50 cm (0.5 m). If the current flowing through the solenoid is 5 A, what is the magnetic field strength inside the solenoid?
Given:
– Number of turns (N) = 1000
– Length of the solenoid (L) = 0.5 m
– Current (I) = 5 A
Step 1: Calculate the number of turns per unit length (n)
n = N / L = 1000 / 0.5 = 2000 turns/m
Step 2: Calculate the magnetic field strength (B)
B = μ₀ * n * I
B = (4π × 10^-7 T m/A) * (2000 turns/m) * (5 A)
B = 1.257 × 10^-2 T = 12.57 mT
Therefore, the magnetic field strength inside the solenoid is 12.57 mT.
These examples demonstrate how to use the formula to calculate the magnetic field strength inside a solenoid, given the number of turns, length, and current. By varying these parameters, you can explore the relationship between the different factors and the resulting magnetic field.
Practical Considerations and Applications
Solenoids are widely used in various applications, and understanding their magnetic field characteristics is crucial for designing and optimizing these devices. Here are some practical considerations and applications of solenoids:
-
Electromagnets: Solenoids are commonly used to create electromagnets, which are used in a variety of applications, such as electric motors, generators, and magnetic separation devices.
-
Particle Accelerators: In particle accelerators, such as cyclotrons and synchrotrons, solenoids are used to create strong, uniform magnetic fields that guide and focus the charged particles along their desired trajectories.
-
Magnetic Resonance Imaging (MRI): MRI systems rely on powerful superconducting solenoids to generate the strong, uniform magnetic fields required for imaging the human body.
-
Magnetic Levitation: Solenoids can be used to create magnetic fields that can levitate objects, such as in maglev trains, which use this principle for frictionless high-speed transportation.
-
Magnetic Shielding: Solenoids can be used to create magnetic fields that can shield sensitive electronic equipment from external magnetic interference, ensuring reliable operation.
-
Inductive Heating: Solenoids can be used to generate high-frequency alternating magnetic fields, which can be used for inductive heating applications, such as in metal processing and cooking appliances.
-
Magnetic Separation: Solenoids can be used to create strong magnetic fields that can be used to separate magnetic materials from non-magnetic materials, such as in the recycling of electronic waste.
These are just a few examples of the many applications of solenoids and their magnetic fields. By understanding the principles and calculations involved in determining the magnetic field of a solenoid, you can design and optimize these devices for a wide range of practical applications.