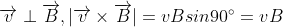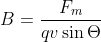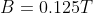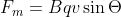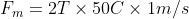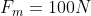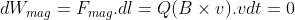Force

Is Magnetic Force a Contact Force?

by
is magnetic force a contact force

Magnetic force is a fundamental concept in physics that has been extensively studied and understood. This blog post aims to provide a comprehensive and technical guide on the nature of magnetic force, specifically addressing whether it is a contact force or a non-contact force.

Definition and Explanation of Magnetic Force

Magnetic force is a type of force that arises from the interaction between magnetic fields and moving charges or other magnets. It is a long-range force, meaning it can act over significant distances without physical contact between the objects involved.

The magnetic force is described by the following equation:

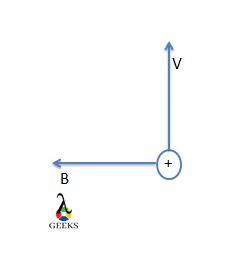
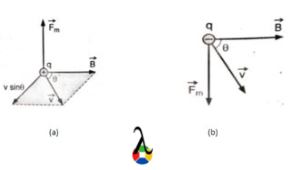
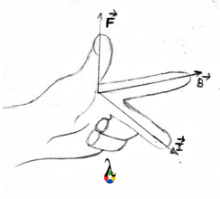
$$\vec{F} = q\vec{v} \times \vec{B}$$

Where:
– $\vec{F}$ is the magnetic force (in Newtons, N)
– $q$ is the charge of the particle (in Coulombs, C)
– $\vec{v}$ is the velocity of the particle (in meters per second, m/s)
– $\vec{B}$ is the magnetic field (in Teslas, T)

This equation shows that the magnetic force is perpendicular to both the velocity of the charged particle and the direction of the magnetic field.

Measurable Data on Magnetic Force

is magnetic force a contact force

Magnetic Field Strength vs. Distance

One of the key characteristics of magnetic force is its dependence on the distance between the interacting objects. Experiments have shown that the strength of a magnetic field decreases with increasing distance from the magnet. This relationship can be expressed mathematically as:

$$B = \frac{\mu_0 m}{4\pi r^2}$$

Where:
– $B$ is the magnetic field strength (in Teslas, T)
– $\mu_0$ is the permeability of free space (4$\pi \times 10^{-7}$ T⋅m/A)
– $m$ is the magnetic moment of the source (in A⋅m^2)
– $r$ is the distance from the source (in meters, m)

By plotting the magnetic field strength as a function of distance, a clear inverse relationship can be observed, demonstrating the non-contact nature of magnetic force.

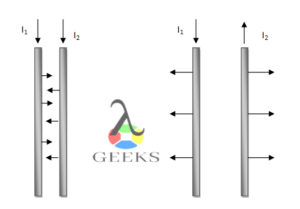
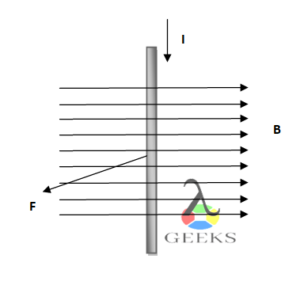
Force on a Current-Carrying Wire

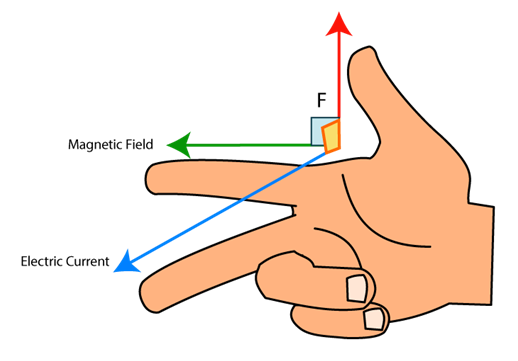
Another way to measure the magnetic force is by considering the force exerted on a current-carrying wire placed in a magnetic field. The force on the wire is given by the equation:

$$\vec{F} = I\vec{L} \times \vec{B}$$

Where:
– $\vec{F}$ is the magnetic force (in Newtons, N)
– $I$ is the current in the wire (in Amperes, A)
– $\vec{L}$ is the length of the wire (in meters, m)
– $\vec{B}$ is the magnetic field (in Teslas, T)
– $\theta$ is the angle between the current and the magnetic field (in radians)

This equation shows that the magnetic force on the wire is proportional to the current, the length of the wire, and the strength of the magnetic field, but it is independent of the distance between the wire and the magnet, further demonstrating the non-contact nature of magnetic force.

Deflection of a Compass Needle

Another experiment that can be used to study the magnetic force is the deflection of a compass needle as a function of distance from a magnet. It has been observed that the deflection of the compass needle decreases as the distance from the magnet increases, again confirming the non-contact nature of magnetic force.

Theoretical Explanation of Magnetic Force

The magnetic force is a result of the interaction between magnetic fields and moving charges or other magnets. This interaction is mediated by the exchange of virtual photons, which are the force carriers of the electromagnetic force.

When a charged particle moves through a magnetic field, the magnetic force exerted on the particle is perpendicular to both the velocity of the particle and the direction of the magnetic field. This is because the magnetic force is a cross product of the velocity and the magnetic field, as shown in the equation earlier.

The magnetic force is a non-contact force because it can act over significant distances without physical contact between the objects involved. This is due to the fact that the magnetic field can extend beyond the physical boundaries of the magnet or current-carrying wire.

Examples and Applications of Magnetic Force

Maglev Trains

One of the most prominent applications of magnetic force is in the design of maglev (magnetic levitation) trains. These trains use strong magnetic fields to levitate the train above the track, eliminating the need for physical contact and reducing friction. This allows maglev trains to achieve much higher speeds than traditional rail-based transportation.

Medical Equipment

Magnetic force also plays a crucial role in the design and development of medical equipment. Clinical engineers use data related to magnetic fields to ensure that new medical devices do not interact with other devices or implants in a way that could cause harm to patients. This is particularly important for devices that use strong magnetic fields, such as MRI (Magnetic Resonance Imaging) machines.

Numerical Problems and Calculations

Problem 1: Calculating the Magnetic Force on a Moving Charge

A charged particle with a charge of 1.6 × 10^-19 C is moving at a velocity of 1 × 10^6 m/s in a magnetic field of 0.5 T. Calculate the magnitude of the magnetic force acting on the particle.

Given:
– Charge of the particle, $q = 1.6 × 10^-19 C$
– Velocity of the particle, $v = 1 × 10^6 m/s$
– Magnetic field strength, $B = 0.5 T$

Using the equation for magnetic force:
$$F = qvB\sin\theta$$

Since the velocity is perpendicular to the magnetic field, $\sin\theta = 1$. Therefore, the magnetic force is:
$$F = (1.6 × 10^-19 C) × (1 × 10^6 m/s) × (0.5 T)$$
$$F = 8 × 10^-13 N$$

Problem 2: Calculating the Magnetic Field Strength at a Given Distance

A bar magnet with a magnetic moment of 0.5 A⋅m^2 is placed in a vacuum. Calculate the magnetic field strength at a distance of 0.2 m from the magnet.

Given:
– Magnetic moment of the magnet, $m = 0.5 A⋅m^2$
– Distance from the magnet, $r = 0.2 m$

Using the equation for magnetic field strength:
$$B = \frac{\mu_0 m}{4\pi r^2}$$

Substituting the values:
$$B = \frac{(4\pi × 10^-7 T⋅m/A) × (0.5 A⋅m^2)}{4\pi (0.2 m)^2}$$
$$B = 0.125 T$$

These numerical problems demonstrate the application of the equations and principles discussed earlier, providing a deeper understanding of the quantitative aspects of magnetic force.

Conclusion

In conclusion, magnetic force is a non-contact force that arises from the interaction between magnetic fields and moving charges or other magnets. The measurable data, including the inverse relationship between magnetic field strength and distance, the force on a current-carrying wire, and the deflection of a compass needle, all support the non-contact nature of magnetic force.

The theoretical explanation of magnetic force, based on the exchange of virtual photons, further reinforces the understanding of magnetic force as a long-range, non-contact force. The examples and applications of magnetic force, such as in maglev trains and medical equipment, highlight the practical significance of this fundamental concept in physics.

By providing a comprehensive and technical guide on the nature of magnetic force, this blog post aims to equip physics students and enthusiasts with a deeper understanding of this important topic.

References

  1. Griffiths, D. J. (2013). Introduction to Electromagnetism (4th ed.). Pearson.
  2. Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics (10th ed.). Wiley.
  3. Serway, R. A., & Jewett, J. W. (2014). Physics for Scientists and Engineers (9th ed.). Cengage Learning.
  4. Tipler, P. A., & Mosca, G. (2008). Physics for Scientists and Engineers (6th ed.). W. H. Freeman.
  5. Young, H. D., & Freedman, R. A. (2016). University Physics with Modern Physics (14th ed.). Pearson.

What Can Exert A force: Exhaustive Insights and Facts

by
istockphoto 1247728090 170667a 1

Can an inanimate object exert a force In this article, we will discuss What Can Exert A force.  

Force is a push or pull induced by the interaction between two objects. So, it is true to say that force can be exerted by the interaction of two objects. Once the interaction ends, objects do not experience the force anymore. Interaction is the fundamental way for forces to arise.  

But the question arises that What Can Exert A force or of what kind of interaction should take place between two objects to exert force or Can an inanimate object exert a force . Do it necessary to establish a contact between two objects to exert force or force can be exerted by any kind of interaction.   

To understand it in a better way, all interactions between objects are divided into two broad categories:   

Contact force

When two interacting entities are considered to be bodily engaging with each other, contact forces occur.

“Frictional forces, tensional forces, normal forces, air resistance forces, and applied forces are all examples of contact forces”.  

Can an inanimate object exert force: What Can Exert A force
Image credit:
What can exert a force

The force produced from the action at a distance (non-contact force)

This type of force is experienced when two objects are not bodily engaged with each other but can still impose a push or pull regardless of their bodily separation.

Gravitational force is example of force produced due to action at a distance. Sun and other planets have a very large distance between them but still, there is a force exerted by the sun and planets on each other. This force between the sun and other planets is also an example of force-producing from the action at a distance.

When we walk and our feet leave the earth’s surface and are no more in touch with the earth, even then there remains a gravitational force between our feet and the Earth.

Electric forces also act at some distance. After having short distance separation, protons inside the nucleus and electrons outside the nucleus feel a force of attraction with each other.

On the other hand, Magnetic forces are action-at-a-distance forces. Two magnets, for example, can exert a magnetic force on each other despite being distanced by only a few centimeters.   

Do all objects exert force ?

What Can Exert A force?

All objects exert force on each other while they are bodily engaged but even if two objects are not in physical touch, they exert a gravitational force of attraction on each other.

True, however, humans aren’t aware of such forces since nobody on Earth has an enormously high mass. As a result, the force of gravity among the two items is so small that they are undetectable. Since the attractive force of gravity between two bodies in a place is relatively low due to their modest masses, they do not push or pull towards one other.

The force of gravity is used by objects with mass to exert forces on one other.

“Magnitude of this force is directly proportional to the product of masses of two interacting objects and inversely proportional to the square of the distance between them.” 

Newton’s law of Gravitation: F_{g}= -\\frac{GmM}{r^{2}}  

For all masses at the Earth’s surface, the parameters G, M, and r are the same. These components are added together to get the constant g, which we refer to as the acceleration due to gravity.  

g= \\frac{GM}{r^{2}}=\\frac{6.67\\times 10^{-11}Nm^{2}/kg^{2}\\times 5.98\\times 10^{24}kg}{(6.37\\times 10^{6}m)^{2}}=9.8 m/s^{2}  

The force of gravity imposed by the Earth on a body of mass m has a value of mg and is aimed downwards at the Earth’s surface. 

Can an inanimate object exert a force ?

Yes, even inanimate objects can exert force. When you stand on a trampoline, for example, the trampoline deforms under your weight, exerting an upwards pressure on you to keep you from falling through.

Because the interactions between atoms and molecules are similar to those between the spring and stretchable fabric that make up a trampoline, when a pencil is placed on a desk, both the pencil and the desk are somewhat distorted. Although the distortion is too slight to see, the forces that cause it to keep the pen from going through the desk. 

 

Does a physical object have to exert force ? 

As we discussed before that the force is a push or pull and occurs due to interactions of two bodies. 

Equal and opposing action-reaction force pairings are always present.  For example; Nature has a wide range of action-reaction force pairings. Consider a fish’s ability to move across the water. The fins of a fish are used to push water backward. On the other hand, a push on the water will simply serve to speed it.

Because reciprocal contacts produce forces, the water sh\uld likewise be forcing the fish ahead, propelling it through the water. The pressure felt by water is same as the pressure felt by fish in magnitude but the direction of the pressure felt on water is backwards while direction of pressure felt by fish is forward. There is an equivalent (in size) and opposing (in direction) response force for every action. Fish can swim because of action-reaction force pairings.  

According to newton’s third law, “For every action, there is an equal and opposite reaction.” Or Force occurs in pairs and they act on different bodies.   

This law means that for every interaction, two main forces are operating on the two engaging bodies in each interaction.

“The forces acting on the first object are equivalent to the forces acting on the second object. The force on the first object is directed in the opposite direction as the force on the second object.”

Can a particle exert force on itself ?

In classical physics, particles do not apply forces to themselves since the classical models that were efficient at forecasting the state of systems did not need them to do so.  

In classical mechanics, one might now establish a rationale. According to Newton’s laws, every action has an equal and opposite response. If I exert 100N of force on my table, it responds by exerting 100N of force in the other direction.

Consider this: a particle that exerts a force on itself is then pushed back in the opposite direction by itself with an equal force. It’s as though you’re squeezing your hands together tightly. You exert a great deal of power, yet your hands don’t move since you’re simply pushing against yourself. You push back every time someone pushes you. 

In quantum mechanics, things are starting to get more fascinating. Avoiding digging into the finer details, quantum physics reveals that particles do interact with one another. And they have to interact with their interactions, and so forth. So, if we get down to the most basic levels, we can witness significant particle self-interactions. This self- interaction of particle is not observed in classical mechanics.    

Can a block exert a force on itself ? 

A body cannot accelerate itself by exerting a force on itself. If it could, things would’ve been able to speed without having contact with their surroundings. Pulling on your bootstraps will not help you get up.

The conservation of momentum is similar to the statement that the resultant force in a closed system is zero, and the law of conservation of momentum may be inferred from the uniformity of space. A mathematician named Emmy Noether confirmed this fact a long time ago.  

Newton’s Second Law states, “the time rate of change of the momentum of a body is equal in both magnitude and direction to the force imposed on it.”

So by this law, a body cannot exert a net force on itself. If you exert a force F on your body with your hands, your body will exert an equal and opposite force F on your hands, resulting to the net zero force on your body. 

 

Why do particles exert force  

Because of the close proximity of particles, particles exert a powerful force force. 

The particles are held very held together and they interact with each other. Their connection resulted in an attractive force between them. The intermolecular force of attraction attracts particles. This force is very powerful.

Why do charges exert forces on each other  

As we study electrodynamics, charged particles interact with each other.

Charged particles have an intrinsic fundamental property that like charges repel each other and unlike charges attract each other, a force called electrostatic force is brought among charges due to this intrinsic property of charges.

This force is quite similar to the Gravitational force of attraction but the basic difference between the two is coulombs force can be repulsive as well as attractive while the gravitational force is only an attractive force.   

“This force is directly proportional to the product of the mass of charges and inversely proportional to the square of the distance between those two charges”.

The electric field might also explain this. The features of the space enclosing a charged body vary, allowing it to function as an interaction channel among two charged bodies applying force on one another.  

How does air inside a container exert pressure  

Because of high kinetic energy and negligible force of attraction or weak intermolecular forces, gas particles can move in every direction at very high speed.

Due to the strong random mobility of the particles, they collide with one another and with the container’s walls. The pressure on the container walls is caused by the interactions of the air molecules with the container walls.  

Why can’t a body exert a net force on itself 

Because of newton’s second law of motion

If you exert a force F on your body with your hands, your body will exert an equal and opposite force F on your hands. As a result, there is no net force operating on your body.  

So by this law, a body cannot exert a net force on itself.

Frequently asked questions| FAQs  

Q. How do you find the force an object exerts?  

One can calculate the force exerted on an object using newton’s second law of motion   

Newtons are used to measure force, kilograms are used to measure mass, and meters per second squared are used to measure acceleration. 

“The force applied by a body is proportional to its mass times its acceleration”: F = m a. You must use SI units to use this formula

Q. What are some examples of force pairs?  

Cars can travel along a highway surface thanks to action-reaction force couples.

As a car moves on the road, the wheel holds the road and exerts a force backward on-road, and the road exerts a force on wheal in forwarding direction. This is a classic example of action-reaction force.

“For every action, there is an equal and opposite reaction.”  

Q. What force the object will apply in reaction of the force applied by you on object? 

Will be equal and opposite   

All forces acting on two objects are of equal magnitude and opposing direction. Only one of the two bodies determines the amount and direction of the forces in particular cases. If you apply a force on an inanimate item, you will also define the force that the object imposes on you – a force that is equal to and opposite to yours.

Q. How many types of fundamental force are there?  

Fundamental forces are divided into four categories. Four basic forces determine how things or particles engage and how some particles decline: gravitational, electromagnetic, strong, and weak.   

 

Also Read:

Magnetic Force Examples: Detailed Insights

by
Capture2 300x209 1

In this article, we are going to discuss some magnetic force examples and understand its application in more detail.

Following is a list of some examples and applications of a magnetic force that we are often using and are basically working on the application of a magnetic force:

Examples of the Magnetic Force and Some Application

Magnetic force can be converted to another form such as mechanical to mechanical in attraction and repulsion; mechanical to electrical in generators, microphones; electrical to mechanical in motors, loudspeakers; mechanical to heat energy as eddy current, hysteresis torque devices, etc. and hence magnetic force has wide application in industries, factories, electronic devices, laboratories, etc. Let us discuss some examples of the magnetic force.

Two Bar Magnets

The bar magnet has two poles, one pole of the magnet carries more number of protons having a positive charge, thus making it positive, and another pole constitutes more number of electrons, hence negatively charged.

The positive pole of the magnet will tend to attract towards the negative pole of another magnet as the positive pole with more number of protons will tend to attract electrons from another pole of the magnet towards it and vice versa, thus both showing the forces of attraction towards each other.

Similarly, when two positive or negative poles are bought closer to one another, will show repulsion as the pole already having a majority of the protons will not accept more protons towards it, or a pole with the majority of the electrons will not pull more electrons towards it, hence the force of repulsion is seen by both the poles of the magnet.

This follows Newton’s Third Law, according to which “Every action has an equal and opposite reaction.”The magnitude of the force experienced by each of the poles during attraction or repulsion is always equal, and the force always acts in the opposite direction.

If the positive pole of the magnet is brought closer to the neutral object, then the electrons from the object will get attracted towards the positive charges thus gathering at one side of the object and repels the protons away from it leaving behind the protons on the other side. And thus, the protons and the electrons will get separated from the neutral object forming two different poles of the charged particles.

Current carrying wire

magnetic force examples
Conductor placed in a magnetic field

The above diagram represents the conductor of length “L” carrying a current “I” placed in the magnetic field. On application of current, the charges in the conductor will show some mobility and an effect so produced due to the presence of magnetic field is called electromagnetism. The force experienced on the unit length of the wire is given as

F=I(L*B)

If is an angle between the current-carrying wire and the direction of a magnetic field, then the magnitude of the force is

F=ILB\sinθ

This equation shows the relationship between current and a magnetic field.

Two parallel current-carrying wires

magnetic force examples
Force of attraction and repulsion by the current-carrying conductor based on the direction of the current.

Consider two current-carrying wires placed parallel. The magnetic field produced by a current-carrying wire 1 at a distance r from it is given by

B=μ0I1/2πr

The force experienced due to the presence of the second current-carrying wire in parallel with the first carrying current I2 is

F=I2LB1

F=μ0I1I2L/2πr

The force per unit length

F/L=F=μ0I1I2/2πr

The two wires will show some force of attraction when the current flowing in both the wires is in the same direction, likewise, both will repel away if the direction of current is in the opposite direction.

Some applications of the magnetic field

Compass

A compass is a device used to find the direction. It consists of a magnetic needle mounted on a small pin that always points towards the North Pole of the Earth. Since the Earth’s magnetic field is positioned in the North-South direction, the magnetic needle gets align itself in collaboration with the magnetic effect felt due to Earth’s magnetic field.

MRI Scanners

Magnetic Resonance Imaging machines are widely used in medical diagnoses. They produce large magnetic field strength and are used to take pictures of the human organs for detailed studies by passing the radio waves.

Electric Motors

A coil in a motor generates a magnetic field on the application of current. The magnetic field thus produces induces magnetic force with the magnet that causes motion or spinning of the motor. So basically, the magnetic force is utilized by the motor to create mechanical energy from electrical energy.

Speakers

Speaker, microphones are devices that come with an electromagnet that converts the electric signal into audible sound. The electromagnet is like a coil, when current flows through this coil it produces a magnetic field. This coil frequently attracts and repels from the magnet to produce an audio effect.

Refrigerators

Refrigerators have a magnet embedded in their door made up of weak ferromagnetic ceramics like barium ferrite or strontium ferrite. Due to this, the refrigerator door always apt to close itself whenever the refrigerator is opened.

Microwave

Ovens have a magnetron which is a vacuum tube designed to generate or amplify the microwaves by controlling the flow of an electron by applying an external magnetic field. A magnet is placed around this vacuum tube that provides magnetic force and causes the electrons to move in a loop. Thus generating heat and cooking food.

Cars

The car uses electromagnetic property inside the engine for its motion. A magnetic coil is attached to an axle. By turning this magnetic coil, the wheels are also made to turn, thus controlling the steering of the car.

Fans

The magnets in the rotor of a fan are repelled by the stators which increase the movement of the rotor. The electric current switches one of the sets of the magnet and hence, the rotor and stator repel themselves away from each other every cycle of the rotor. This is achieved by the application of the magnetic force.

Magnetic Force

Magnetic force is one among the four fundamental forces. The magnetic force acts perpendicular to the motion of the particles, thus opposing the motion of the charges; hence the charged particles tend to deflect due to the magnetic force. 

The magnetic force depends upon the charge and the velocity of the particle in a magnetic field and the external field applied to the conductor and is given by F=qvB. In presence of the external field, the electrons and protons align themselves according to the field applied. The magnetic field density depends upon the density of a magnetic flux crossing per unit cross-sectional area of the material.

Types of magnetic force

1) Attractive Force: When two poles of unlike charges are bought near, both the poles tend to attract towards each other. The force exerted by the poles on each other is known as an attractive force.

2) Repulsive Force: When the two poles of like charges are bought near, the poles repel away from each other. The force felt on each of the poles is known as a repulsive force.

Theory and the Classification of Magnetic Materials

According to the Pauli Exclusion Principle, “No two electrons will have the same quantum number. No more than two electrons can occupy the same orbital. Electrons present in the same orbital must have opposite or anti-parallel spin.”

The electrons pair up with the electrons having an opposite spin and canceling out the magnetic moment produced by each other. Well, the unpaired electron shows the spin and orbital movement of the atom and gives the direction of the magnetic field.

Based on the number of free electrons available, various materials show different magnetic characteristics. If the number of available unpaired electrons is greater, then, the magnetic effects seen in the material will also escalate. The materials are classified as follows:-

Diamagnetic: Diamagnetic materials show the force of repulsion on both the poles of a magnet. These materials tend to oppose the magnetic flux through them and hence are repelled by the magnetic force. Examples: Carbon, Gold, Silver, water, etc.

Paramagnetic: Paramagnetic materials show properties of magnetization only when a strong magnetic force is applied to them. They are weakly attracted to either of the poles of a magnet. Examples: Oxygen, Aluminum, brass, etc.

Ferromagnetic: Ferromagnetic materials are highly magnetized materials. They have many unpaired electrons which are aligned forming colonies of charges and hence becoming highly attractive. They can retain their magnetization and even become a magnet. Examples: Iron, Nickel, Cobalt, etc.

On what factors does the magnetic force depend

The magnetic force basically depends upon the magnitude of the charge, the velocity of a charged particle, and the external magnetic force. In the electromagnetic region, this force is described as Lorentz force and is represented as:

F=q(E+v*B)

Force due to the magnetic field is given as

F=qvB

The magnitude of the magnetic force

F=qvB sin θ

Where θ varies from 0 to 1800 and <1800.

The direction of the force is found out using Fleming’s Right-Hand Rule and Right-Hand Grip Rule as shown below,

Right Hand Grip Rule

image
Right-Hand Grip Rule, Image Credit: Electrical4dummies

The right hand is imagined as the current carrying conductor. The direction of the current is symbolized by the thumb and the field lines are running around the conductor forming concentric circles as seen in the figure.

Fleming’s Right-Hand Rule

Magnetic Force
Fleming’s Right-Hand Rule, Image credits: Electrical4dummies

In Fleming’s Right-Hand Rule, the thumb shows the direction of force, while the index and middle finger indicate the direction of magnetic field and electric current respectively.

For a current carrying conductor placed in a magnetic field, the force experienced on a unit cross-section length of the wire is given as

F=qvB sin θ

because, velocity = distance/time

Hence, we can rewrite the above equation as:

F=a/LTBsin θ

Current is defined as a charge per unit time and given by I=q/t

Therefore, F=BILsin θ

Read more on “What Objects Have Magnetic Force: Exhaustive Facts On Various Objects“.

Frequently Asked Questions

What force is a magnetic force?

The magnetic force depends upon the majority of the charge carriers, the direction of a field and the current.

The magnetic force is basically the force of attraction and repulsion between the positive and the negatively charged particles.

Consider a wire placed between the two poles of the magnet. If the current flowing in a wire is 15A, find the magnitude and the direction of the force experienced on 10 mm length of the same wire if the magnetic field is 0.2T.

A magnetic field is perpendicular to the direction of the current flowing in the wire, therefore

sin θ=1

The force experienced on a 10mm section of the wire is

F=BIL=0.2T*15A*0.01m=0.01N

If the magnetic field lines are running towards North and the acceleration of the electrons is perpendicular to the direction of the field, then the force is exerted outward.

What material is used to make a horseshoe magnet?

A horseshoe magnet is a U-shaped magnet and both the poles are in the same direction that helps to create a strong magnetic field.

It is made up of AlNiCo an alloy of Iron and an iron bar is attached to the two poles of the magnet to prevent demagnetization. This was previously used in microwave ovens in the magnetron tube.

Also Read:

Is Gravity An External Force:Exhaustive Insights

by

There is the external and internal force that could be studied depending on the type of work. Let us see in detail about is gravity an external force.

It is possible to have various forms of forces that will never affect the overall mechanical energy of an item but will instead just transfer the energy of an object from potential to kinetic energy (or vice versa). Internal forces and external forces are the two types of forces that may be found in a given circumstance.

In this article, we will study is gravity an external force or an internal force by comprehending the ideas of internal and external forces.

Is gravity an external force?

Gravity is not an external force.

The gravitational force or gravity between two particles in a system is defined as when two particles in a system are attracted to one another. When we investigate gravitational force, we are looking at the interaction of two or more particles. Moreover, the gravitational pull conserves the overall amount of energy. As a result, gravity is considered an internal force.

External Force Vs. Internal Force

Many classification systems are used to classify the various kinds of forces.

It was stated that all forces might be classified as contact or action-at-a-distance. A force’s classification as an action-at-a-distance force depends on whether it may exist even when objects are not physically touching. Even if two items aren’t physically touching, they can still be affected by forces like gravity, electricity, and magnetism.

It is possible that some types of forces, when present and when involved in the performance of work on things, will cause the total mechanical energy of the item to be altered. A force that can never have an effect on an item’s total mechanical energy, but can only transfer the energy of an object from its potential to its kinetic state, is referred to as a kinetic energy. 

Internal forces and external forces are the two types of forces that may be found in a given situation. So, that means internal and external forces based on whether or not their existence has the capability of altering the overall mechanical energy of an object.

There are numerous excellent approaches to explain and distinguish internal and external forces. However, for the purposes of this discussion, we will logically conclude that external forces are comprised of the applied force, the normal force, the tension force, the friction force, and the air resistance force. However, internal forces comprise gravity, magnetic, electrical, and spring forces for our needs.

Non-conservative and Conservative forces

In order to understand the significance of classifying a force as either internal or external, it is necessary to understand how that type of force may modify the total mechanical energy of an item when it performs work on that object.

Non-Conservative Force:

A change in the total mechanical energy (KE + PE) of an item occurs when net work is performed on it by an external force. It is possible for an item to gain energy if the work is positive. It is possible for an item to lose energy if the work is negative. The increase or decrease in energy might take the form of potential energy, kinetic energy, or a combination of the two. In such conditions, the amount of work completed will be equal to the amount of mechanical energy that has been changed in the item.

“Nonconservative forces” refer to external forces that have the ability to modify the total mechanical energy of an object due to the fact that they have the power of affecting the total mechanical energy of an object.

Conservative Force:

It is possible for an object’s total mechanical energy (KE + PE) to remain constant even if the object’s principal source of net work is internal force (for example, gravitational and spring forces). When this occurs, the object’s energy takes on a different form. In the case of an object “forced” to drop from a high height to a low elevation due to gravity, part of the potential energy of the object is converted into kinetic energy as a result of gravity.

Conversely, the total amount of kinetic and potential energy remains constant during the experiment. Energy conservation is the term used to describe this.

However, when internal forces are the sole ones conducting the work, energy can alter forms, going from kinetic to potential (or vice versa), but the overall value of mechanical energy is conserved. It is for this reason that internal forces are sometimes referred to as conservative forces because they are capable of modifying the form of energy without increasing the total quantity of mechanical energy contained inside a system.

The above explanation is simply the detailed answer on is gravity an external force.

Internal force examples

Internal forces – gravitational and spring forces – are the only ones that perform work on the items described in the following examples. This results in the transformation of energy from KE to PE (and vice versa), while the overall quantity of mechanical energy is preserved. How the energy is transferred between KE and PE should be the subject of each description.

1. If in the absence of air resistance, a ball falls from a height of 2 meters.

→ A decrease in height (dropping) and an increase in velocity are being experienced by the ball. In order to do this, the internal or conservative force (gravity) is used to convert energy from Potential Energy (height) to Kinetic Energy (velocity).

2. When a dart is launched from its original resting position, the spring of a dart gun exerts a force on the dart.

→ After undergoing a transition from a compressed to a relaxed condition, the spring is forced forward, propelling the dart onward. This transition causes the internal or conservative force (spring) to transfer energy from Potential Energy (a compressed spring) to Kinetic Energy (speed).

Frequently Asked Questions (FAQs):

Q. What do you mean by an external force?

Ans: Any body can feel force externally or internally.

An external force is defined as the force applied to an item from the outside. It can be either a contact or a non-contact force. An external force is mostly a contact force, which occurs when an item interacts with its environment. 

Read more on the external force examples in detail.

Q. What are different types of an external force?

Ans: There are five types of an external force

Read more on the types of external force

Q. What do you mean by internal force?

Ans: On the basis of their interaction with the system, forces are classified as internal or external forces, respectively.

When a force operates on a system internally, it is referred to as an internal force. This force either causes a change in the system or opposes a change in the system caused by an external force. In a system, internal forces are generated within the system, and they are unable to cause an external change in the system, such as an acceleration of the system or a change in the system’s kinetic energy.

Read more on examples of the internal force.

Q. What are the different types of internal force?

Ans: There are four types of an internal force.

  • Bending
  • Compression
  • Tension
  • Torsion

Also Read:

What Objects Have Magnetic Force: Exhaustive Facts On Various Objects

by
Unlike 300x91 1

In this article, we are going to study what objects have magnetic force and possess a force relevant to the field.

The two objects with a motion of charges in the same direction experience a magnetic force of attraction, whereas, the objects with charges moving in the opposite direction show repulsive force between them.

What is a Magnetic Force?

A magnetic field is produced when a conductor is placed in the electric field; an electromagnetic force is induced in the conductor due to the motion of the unpaired electrons.

The force experienced by the particle in the field opposing their motion is a magnetic force. A magnetic force may be attractive or repulsive based on the alignment of the magnetic dipoles inside the material.

Types of the Magnetic Force

Attractive Force: When the two objects having the dipoles arranged in the same direction tend to attract towards each other, the force experienced by the objects on each other is known as an attractive force.

What objects have magnetic force
Unlike poles attracts

Repulsive Force: Two objects having the dipoles arranged in the opposite direction tends to repel from each other, the force exerted by the objects on each other is called repulsive force.

Magnetic Force repels
Like poles repels

Do all objects have a magnetic force

The electrons pair with the opposite spin, which results in the cancellation of the magnetic field produced by each of the electrons. When the magnetic field is set up in the material, positive and negative carriers inside the material become mobile and arrange according to the external field exerted.

If the number of electrons available is greater, then, the magnetic effects seen in the material will also escalate. Based on these, the materials are classified as follows:

Diamagnetic: Materials that have no unpaired electrons shows diamagnetism, these material tends to oppose the magnetic flux through a unit cross-sectional area and are hence repelled by the magnetic force. Examples: Gold, Copper, Silver, H2O.

Paramagnetic: Material has an unpaired electron, and these unpaired electrons tend to align themselves in the direction of the applied external field, hence showing magnetic behavior in presence of the external field. Examples: Aluminum, Di-Oxygen, Lithium.

Ferromagnetic: Material is strongly magnetized in presence of the magnetic field and retains its magnetic property even in absence of the external magnetic field.  Examples: Iron, Nickel, Cobalt.

Read more on What Produces the Strength of a Magnetic Field.

What objects use magnetic force

The application of the magnetic force is widely used due to its attractive and repulsive behavior.

Devices like electric motors, door latches, speakers, data storage devices, refrigerators, compass, clinometers, microwaves, cars, etc. use a magnet.

Let us discuss some examples below to get an idea of the commonly used objects in our day-to-day life and whether these objects show magnetic behavior or not.

Is a paper magnetic

No. Paper is a bad conductor of heat and electricity as it is made up of carbon. A carbon atom has atomic no. 6 having 4 electrons in its outermost shell, which is a half-filled electronic configuration of an atom and the most stable state of the atom. The spin of all six electrons cancels the magnetic moment produced by each thus making the total magnetic moment zero. Hence, carbon shows no magnetic behavior.

Is glass magnetic

Glass is manufactured using Silicon Dioxide, Calcium Carbonate, and sodium carbonate. Silicon is a semiconductor, that is, it partly behaves as a conductor and partly as an insulator. It is a dielectric and can transmit electric force without conducting.

When the external field is very strong, the dipoles of the silicon glass may align in the direction of the fields. Glass has very low permeability and hence shows diamagnetic characteristics, but the percentage of composition of these elements is very negligible to make the glass magnetic. Some glasses are also made up of cobalt which shows magnetic behavior.

Is an iron nail magnetic

Yes, an iron nail is magnetic. The atomic number of Iron [Fe] is Z=26. The electronic configuration of this element is given by [Ar]3d64s2. The valence electron of Feis 8 and has 4 unpaired electrons. Hence, iron shows ferromagnetism and retains its magnetic property even in the absence of an external field.

Is a wood magnetic

Wood is an insulator. It is a bad conductor of heat and electricity, and hence no field is induced inside the wood and no field of attraction appears.

Is gold magnetic

Pure gold is not magnetic but shows magnetic behavior in presence of an external field. The electronic configuration of Ag: [Xe] 4f145d106s1. The 6s orbital has one unpaired electron which is a half-filled shell. Because of this unpaired electron, gold shows diamagnetic behavior in presence of the external field. Moreover, the magnetism of alloy of gold depends upon which metal is used to make an alloy with gold.

Is brass magnetic

Under normal circumstances, brass is not magnetic at all. It’s only when the strong magnetic field is applied to the brass metal, the electric current is set up inside the metal. This follows Lenz’s Law. When an electric current is set up inside the metal, it will show some interaction with the magnet.

Brass is an alloy of Copper [Cu] and Zinc[Zn] and shows a slight diamagnetic effect in presence of an external field, but it is very small to be noticed.

Is silver magnetic

The atomic number of silver [Ag] is 47 and the electronic configuration of Ag is [Kr]4d105s1. It has a half-filled, stable 5s orbital with one unpaired electron. Silver is not magnetic but will show some interaction with a strong magnet under the influence of Lenz Law which states that the current induced in the circuit due to the motion of the charged particles is directed to oppose the change in flux and hence exerts a force opposing the velocity of the particles.

The magnetic moments induced will produce an eddy current within the silver metal. This eddy current is responsible for the interaction of the metal with magnet. Hence, silver shows diamagnetism in presence of an intense magnetic field.

Are whiteboards magnetic

Whiteboards are not magnetic. Whiteboard mostly has steel sheets that provided magnetism across the surface of the board. Steel is an alloy of iron that has ferromagnetic characteristics.

What metal is magnetic

Magnetic materials are attracted towards the magnet and may even become magnetized. The ferromagnetic metals will definitely show magnetic effects naturally because they are magnetized. Even, the metals made from the alloys of the ferromagnetic material will show magnetic behavior. 

Is a chalkboard magnetic

Chalkboards are not magnetic but can be made magnetic using galvanized steel and by applying magnetic primer.

Is a penny magnetic

No. Penny is a coin made up of Bronze, an alloy of 95% copper and 5% Tin and Zinc. This alloy does not show any magnetic behavior.

Is plastic attracted to magnets

No. Polyethylene is the most commonly used plastic nowadays. Plastic is a bad conductor of heat and electricity, known as an insulator; hence does not consist of magnetic properties.

Is nickel magnetic

Yes. Nickel has atomic number 28. The electronic configuration of nickel is [Ar] 4s2, 3d8 and has two unpaired electrons. Hence, it shows ferromagnetic characteristics.

Can trees be magnetic

No. Wood is a bad conductor of heat and electricity. But, the tree has certain elements that may show magnetic characteristics.

Are Diamonds magnetic

No, because diamonds are made up of carbon which has 6 electrons, and all the electrons pair up with each other which cancels out the magnetic moment produced due to the spin of the electrons. Hence, the total magnetic moment by the carbon atom is nil and does not show any magnetic behavior. But some synthetic diamonds are magnetic because of some inclusions during their manufacturing.

Is Black Sand magnetic

Black sand is formed due to a result of the volcanic eruption. The molten magma is often comprised of Fe-rich lava. The mineral usually found in the area of volcanic eruption with more concentration of iron is magnetite. Magnetite being rich in Fe-concentration is ferromagnetic and hence the black sand is magnetic.

Is an aluminum can magnetic

Aluminum has atomic number 13. Its electronic configuration is 1s22s22p63s23p1. Since Al has only one unpaired electron the paramagnetism is expected, but aluminum is not magnetic under normal conditions. Only when it is introduced in the magnetic field region, small eddy currents are established inside the Al-metal which instigate magnetic dipoles and hence shows paramagnetism.

Is a lead solder magnetic

Lead with atomic no.82, [Xe] 4f14, 5d10, 6s2, 6p2; is not magnetic; but shows weak diamagnetism in presence of external magnetic field as it acquires magnetism in the direction opposite to the field.

Is there magnets in dirt

Yes. When we left the magnet in the open air, we will notice that the magnet will gather some dirt on it. Dirt gets magnetized only when we apply the magnetic field to it.

Is Sugar magnetic

The chemical formula of sugar is C12H22O11. It interacts in electromagnetic fields and thus can be affected by a magnetic field, but is not magnetic.

Is Salt attracted to a magnet

Rock salt shows very weak magnetism as it contains few paramagnetic or ferromagnetic minerals. Salt of cobalt shows very high magnetic behavior. NaCl is diamagnetic; all spins are paired in Na+ and Cl- ions.

Can magnets move water

Water is slightly repelled by a strong magnet. Water has 2 hydrogens and one oxygen atom, when both combine to form water, there are no free electrons left behind to attract anything towards it to pair, hence water is diamagnetic.

Read more on objects that produce a magnetic field.

Frequently Asked Questions

Does a magnet transform one form of energy to another?

A magnet transfers one form of energy into another without any loss of its energy.

Such as mechanical to mechanical in attraction and repulsion; mechanical to electrical in generators, microphones; electrical to mechanical in motors, loudspeakers; mechanical to heat energy as eddy current, hysteresis torque devices.

How a magnet affects the growth of the plant?

It is noticed that the plant grows faster when it is surrounded by a magnet on the soil.

A magnet attracts ferromagnetic elements from the soil towards it, which becomes easier for the roots of the plant to intake these elements and grow at a faster rate.

Also Read:

Kinetic Friction vs Kinetic Force:Detailed Analysis

by
kinetic friction vs kinetic force 0

The kinetic friction and the kinetic force seem like the same quantity, but they are not the same.

Though Kinetic friction and kinetic force are both exerted on the moving objects, let us study the facts which make these two physical quantities differ by analyzing Kinetic friction vs Kinetic force in this post.

Comparison between the Kinetic Friction vs Kinetic Force

 The below table may help you to understand the nature and behavior of kinetic friction vs kinetic force.

Kinetic friction Kinetic force
Kinetic energy Kinetic friction reduces the kinetic energy of the system. This loss of kinetic energy results in releasing heat energy. Since the kinetic force makes the body accelerate more, the kinetic energy increases with increased acceleration.
Nature of the surface The Kinetic friction constantly evolved between the two solid rough surfaces. The surface must be rough. It may be flat or inclined. The kinetic force is exerted only in the inclined plane because in an inclined plane to move upward it takes more force for the motion. Since on the flat surface, the body does not require any force to keep on moving. So that on a flat surface, the acceleration is constant.
Gravity The influence of gravity on kinetic friction is constant as kinetic friction is independent of gravity. Still, the factor involved in the kinetic friction, i.e., the normal force, is influenced by the acceleration due to gravity. Kinetic force is primarily influenced by gravity. The object accelerates rapidly down the ramp because the gravitational pull-down ramp is more.
Net weight The net weight of the object gives the normal force acting on the body, which is responsible for the kinetic friction. The kinetic force is itself considered as a portion of the possible net weight of the object.
Coefficients The ratio of kinetic friction and the perpendicular reaction gives the coefficient of kinetic friction. This is a dimensionless quantity which exerts wide influence over the kinetic friction. The coefficient kinetic force is the wrong terminology to explain the force. Since all the coefficients are dimensionless, quantity is used to express the nature of the physical quantity. But in the case of kinetic friction, it is an irrelevant quantity.
Direction Kinetic friction always acts in the opposite direction to the relative motion of the objects. Kinetic force acting on the moving body is in the direction of the relative motion of the body.
The study of kinetic friction vs kinetic force convinces us how the two forces exerted on the moving body differ from one another.

Definition of kinetic friction and kinetic force

In order to understand the action of kinetic friction vs kinetic force on the object, the definition of them is very helpful.

Kinetic friction is the resistance offered to the moving body to restrict its motion. In contrast, the Kinetic force is probably a net force that is exerted on the object parallel to the plane of inclination that causes the object to accelerate.

kinetic friction vs kinetic force
Kinetic friction vs kinetic force

By the above definition, it is clear that the kinetic friction stops the moving object and the kinetic friction allows the moving object to accelerate more.

Interesting facts to remember

  • When the body moves down the hill, the kinetic force is maximum, moving rapidly. As it moves near the flat surface, the kinetic force becomes minimum, and in some instances, its motion is retarded by the kinetic friction.
  • Both kinetic friction and kinetic force are applied to the types of forces exerted on the body; these are equal and opposite to each other.
  • It is impossible to stand up if the friction acting between our body and the surface is absent.
  • Wheels are used to reduce friction and accelerate rapidly, but the wheel couldn’t work properly without friction.
  • In the case of both kinetic friction and kinetic force, the energy may get lost by releasing some amount of heat.
  • The kinetic friction always retards the kinetic force.
  • In some sense, kinetic force is an uncommon usage term. Kinetic force is considered as the impulsive force which arises due to collision. It is referred to as the contact force and given by Newton’s laws of motion as, Impulse = Ft
  • Kinetic friction is the one responsible for the object’s motion, while kinetic force increases the speed of the movement.

Frequently asked questions

Does the kinetic friction remain constant throughout the motion?

 When the applied force is maximum, and overcomes the stiction, then the kinetic friction evolves.

The kinetic friction remains constant until the body gains the energy to move when the kinetic energy is lost in the form of heat and reaches the threshold motion, the kinetic friction increases.

Does the increase in speed increase the kinetic friction?

No, the increase or decrease in the speed does not alter the kinetic friction at the moderate level.

The kinetic friction always increases when the normal force between the objects increases. When the speed is increased slightly, the kinetic friction remains constant. If the speed is increased to the greater value, the friction offered by the surface becomes negligible.

How does the kinetic energy increase with the kinetic force?

Kinetic force makes the object accelerate more; this helps the energy to exert more on the body.

When the speed of the body increases, the body requires more energy to keep the force steady, the distance traveled by the body increases at a constant force as the force keeps on increasing the kinetic energy increases too.

What is the major application of kinetic friction?

The kinetic friction is mainly applicable in lubrication.

The wear and tear of the machinery depends on the kinetic friction. The car brakes use the principle of kinetic friction, which indeed uses lubrication.

How does kinetic friction be responsible for the motion?

The kinetic friction converts the kinetic energy into heat energy.

When the two surfaces are in contact, and when the force is applied to one surface, it begins to move. The kinetic energy is converted into heat only when the surface of one block slides over another surface. This energy is sufficient to cause motion.

Does the mechanical energy is conserved in the kinetic friction?

Since the kinetic friction reduces the mechanical energy of the system, it is considered non-conservative.

If the total sum of potential energy and the kinetic energy is constant then the energy is said to conserved. In the case of kinetic friction, the energy conversion between the potential and the kinetic energy does not occur. Hence the mechanical energy is not conserved.

How does the kinetic energy equal to the kinetic friction?

The kinetic friction and kinetic energy are not related to one another. Both are different components.

Kinetic energy is the energy correlated to the body in motion. This energy may get reduced if the friction exerted on the body is more. But kinetic energy and the kinetic friction are unequal quantities.

Also Read:

Magnetic Force On Moving Charge:7 Facts & Problems Solution

by
image 1 1

Magnetic Force on moving charge in magnetic field is possible only due to the presence of electric field created by the charges moving from positive end to the negative end.Now let’s see how a magnetic fields are created.

When there is current flowing due to the motion of electric charges produce magnetic fields. When the nucleus of atom orbits continuously then the magnetic force on moving charges in magnetic field is determined.The force on a negative charge is in exactly the opposite direction to that on a positive moving charge.

Fundamentally, when a current is passed over an element electric field is witnessed Here we consider the element to be a solenoid which in turn create magnetic fields in and around the region. This magnetic force exerted on the charge particle will affect any particle entering the field.

It is a known fact that an electric field is produced by static charges and when another charged particle is brought closer it is either attracted or repelled. So in this way, the electric field has a force that will act on the charges present in the electric field.

Similarly, there exists a magnetic force on a moving charge in magnetic fields. Here we will deal with inductors to show how the force on a moving charge in magnetic field is possible. In an electric field, it is capacitors that will be the reason for force on a moving charge.

How charged particle moves in magnetic field

We consider a current filament where electric current flows in a certain direction of the magnetic field is produced in circular form. This filament can also be a solenoid.

At this moment a charge enters the magnetic field region with a certain velocity. Since the magnetic field lines are not similar to the electric field line, they will form a circular path. The charge entering the magnetic field will travel in the circular path as well.

Force on a moving charge on the magnetic field is the process happening basically when a charge passes through the magnetic flux lines. The magnetic fields exert forces by the magnetic flux line on a charge moving within becomes zero if it is parallel to magnetic field lines.

Force on moving charge formula

We are well aware of how the magnetic fields exert forces on a moving charge that comes inside the flux lines. The magnetic field is in right angles to the charge that is undergoing motion.

The magnetic force on moving particle in the magnetic fields is denoted by : F = q V B sineθ.

Lets try to understand the derivation and implementation :

Because the charge does not experience any change in its kinetic energy, since the charged particle moves in a circular motion. So when anything that experiences a circular motion will have zero displacements and the kinetic energy will remain the same.

Considering this we shall determine the formula for magnetic force on a moving charge in magnetic field.

The magnetic flux line or the magnetic fields are denoted by the letter B, the charge that enters and moves inside the magnetic field is denoted by the letter q. The velocity with which the charge moves inside the magnetic field is denoted by the letter V.

When the charge moves inside the magnetic field, the field exert forces on the charge. This magnetic force is related to certain parameters. The parameter for the force magnitude is as explained; it is proportional to the magnitude of the charge, the magnitude of the velocity of the charge under motion, and the magnetic field.

The exert forces by magnetic field proportional to sine θ. Meaning, θ is the angle made by the velocity of the charge that moves with the magnetic flux lines.

Force on moving charge formula (Explanations):

Now the formula for magnetic force on moving charge is F = q V B sineθ.

As in the case of force it is basically a vector quantity having magnitude and direction. The formula mentioned previously is used to calculate magnitude of the force. The direction of the magnetic force is the direction of the charge moving in the magnetic field.

The direction of the magnetic charge travelling inside the magnetic field is in right angles to both the velocity and the magnetic field. The formula for this condition is F = q V B sine θ an.

Therefore when the motion of the charge is right angles to the velocity and the magnetic field the formula is revised and given as F = q (V X B). Because θ becomes 90⁰ and sine 90⁰ is equal to one.

Hence the formula for the magnetic force on moving charge in the magnetic field is given by three different conditions and can be used according to the problems provided.

Moving charge in a uniform magnetic field derivation

A Uniform magnetic field is produced when a current-carrying solenoid is passed with an electric current. This is easily explained using Right Hand Thumb Rule or also called as Lorentz Force.

The above mentioned formula is used to calculate the magnetic force employed on the charge moving inside the magnetic field.

The right-hand thumb rule is defined as; the thumb indicating the direction of velocity, the index finger indicating the direction of the magnetic field (B), and the middle finger indicating the direction of the resultant force.

The right-hand thumb rule is also known as Lorentz Force. The formula of Lorentz Force is F = q V B sine θ. Here q is the charge in the magnetic field, V is the velocity, B is the magnetic field and θ is the angle made between velocity and magnetic field.

Zero force on moving charge:

It is now a known fact that the charge moving inside the magnetic field will undergo a circular motion. The force acting on this will have a different result compared to the conventional one.

When electric current is present in a solenoid, eventually a magnetic is created. The flux lines are in a circular motion that is they are produced around the solenoid.

Hence when a charge moves inside the region of the magnetic field they follow the direction of the magnetic flux lines. A circular motion is eventually created inside. The charge will move in the same direction and then have no change in the kinetic energy.

Since there is no displacement in the whole system the force is said to be zero. The reason is that the charge will go on and on moving in circles in the direction of the magnetic flux lines.

The velocity with which the charge moves inside the magnetic field is parallel to the magnetic field. So the magnetic force on moving charge will be eventually zero.

A charge moving equally parallel in the same direction of the magnetic field, then magnetic force acting that particular magnetic field is zero.

In essence of the work done on the charge in a magnetic field is zero or minimum. In a magnetic field if the kinetic energy of the charge is said be zero the the system obeys work-energy theorem.

Here in this case when the magnetic force becomes perpendicular to the velocity the direction might not change but the magnitude will change. So the word done on the charge will be zero, making the force acting on the charge also zero.

Direction of moving charge in magnetic field:

The magnetic field direction created by a moving charge is perpendicular to the direction of motion of the charged particle. Hence the magnetic force generated due to a magnetic field is perpendicular to the direction of motion of the movement and speed of the charged particle.

Problems and solutions:

Problem 1: Consider a charge to move in the north direction with a speed of 3 x 106 m/s. a magnitude of 4.0T will act in the west direction. Now calculate the magnitude of the force on moving charge in the magnetic field? [The charge moving inside the magnetic field is the proton].

magnetic force on moving charge in magnetic field

Solution:

Let us consider the right-hand thumb rule. The force coming out of the hand is the magnetic force on moving charge.

Magnitude of the force is F = q V B sineθ

F = (1.6 x 10-19C x 3 x 106 x 4 T x sine 90⁰)

F = 1.92 x 10-12 N

Problem 2: Calculates the earth’s magnetic field when the positive moving charge in the system has a velocity 2 x 105m/s moving in the north direction and the magnitude of the force acting on it is 1.2 x 10-13N in the west direction.

Solution:

Formula is F = q V B sine θ

B = F / (q x V x sine θ)

B = (1.2 x 10-13) / (2 x 105 x 1.6 x 10-19 x sine 90⁰)

B = 3.75 T

Therefore now it is clear that the magnetic force on moving charge has different conditions from the explanation and the formulae.

Also Read:

Is Magnetic Field And Magnetic Force Same: Different Aspects And Facts

by
quicklatex.com 30b48bf9527ca56c7b98ca2d673009c9 l3

Magnetic field and magnetic force go hand in hand. In this article, we will discuss the fascinating relationship between these two.

A magnetic field is an actual entity that fills up the space around a current-carrying conductor or moving charge, or magnet. In addition to this the force acted by a magnetic field upon a moving charged particle is magnetic force.

How magnetic field is connected to magnetic force

To understand it more precisely, if we place a static charge in a magnetic field, the charge experiences no force, so to define a magnetic field, we take a charge q which is moving with velocity v in such a field

Fig. 1(a)

 

 

Is magnetic field and magnetic force same
Is magnetic field and magnetic force same

If Fm is the force exerted by the field on the moving charge, then it has been experimentally found that;

  1. Fm ∝ v
  2. Fm ∝ q
  3. Fm ∝ v sinθ

If Fm is the force exerted by the field on the moving charge, then it has been experimentally found that; 

Combining the above three points, we obtain  

Fm= Bqv sinθ …………(1)

Here B is the proportional constant, and it gives the magnitude of the magnetic field. It is also known as magnetic flux density or magnetic field induction, or simply magnetic field. It is a pseudo-vector, and we denote it by B. 

When a magnetic field is exactly equal to magnetic force 

If we consider q=1, v=1 and θ = 90⁰  

From equation (1), Fm= B

So here, we can say that the magnetic field at a point is thus equal to the magnetic force acting on a unit charge when it is moving with unit velocity in a direction perpendicular to the magnetic field. 

In vector notation, Fm= q(B x v)

Obviously, Fm known as magnetic Lorentz force, is perpendicular to the plane containing v and B.

In case,

gif 5

In that case,Fm= qvB

As, Fm= qvB

B= Fm/qv

If  Fm = 1N, q=1C and v = 1m/s 

Then, 1T= N/C(m/s)

1T= N/Ampere

The SI unit of B is called tesla(T)

So, the magnetic field at a point is thus said to be one tesla if a charge of 1 coulomb when moving perpendicular to the direction of the magnetic field with a velocity of 1 meter/second, experiences a force of 1 newton. 

                                                           

Direction of magnetic field and magnetic force

Magnetic field does not flow in direction of its source that is current; instead, it flows normal to the direction of current. Additionally, the magnetic force act perpendicular to magnetic field.  

image 134

Direction of magnetic field can be detected using right hand thumb rule. According to right hand thumb rule; If a current carrying wire kept in hand, then direction of thumb implies direction of current and direction of fingers indicates direction of flow of magnetic field.  

image 135

Example

If we take a bar magnet and bring it to an iron nail, at some point, the nail moves towards the magnet and sticks to it. Moreover, it remains there until we manually separate it from the magnet. So why does an iron nail stick to the magnet?  

Reason behind is the force of attraction that connects the nail and magnet together. This force is applied by the magnet on the nail, and hence it’s called a magnetic force. 

Here is one interesting question that I want you to answer; Is magnetic force is contact force, or in other words, is the contact between a magnet and nail necessary for the magnet to attract the nail?  

When we move the magnet slowly towards the iron nail, and at this point, the nail also begins to move towards the magnet, it means the force came into action even when there was no contact between the magnet and nail. Hence, we can say that magnetic force is not a contact force.  

What does this non-contact nature of magnetic force tell us  

It tells us that there is an invisible field produced by the magnet in the space around it, and if you bring any ferromagnetic material in this field, then it experiences that force of attraction. We cannot see this field, but it exists.  

Now one more interesting question, do you think that strength of this field is constant throughout the area around the magnet?  

Let me explain it in easy way, suppose that there is a operating wireless fidelity router at some location. It provides us a signal altogether directions in some distance. currently so as to connect mobile to the net, we’d like to bring it to during this vary solely. This signal is stronger nearer the router.

“The nearer you bring your cellular phone to the router, the stronger the signal are”.

One can understand the magnet with same approach.  magnet contains a field of force around it. The strength of this field is bigger nearer to the magnet and reduces as we tend to go more far away from it.

As you bring any ferromagnetic object during this field, it experiences an attractive force. The nearer we tend to bring that object to the magnet, the larger the force it’ll expertise till at some purpose once the force are massive enough to create the item leap towards the magnet. 

Problems on magnetic field and magnetic force

Let us understand the relationship of magnetic field and magnetic force by solving some basic problems. 

Problem 1 

Find magnetic field exerted on a charge of 20 coulomb is moving perpendicular to the direction of magnetic field with velocity 2m/s and experiences a force of 5 newton.  

Solution:  

Given magnetic force,  Fm

Velocity of charge particle, v

image 6

Magnetic field, 

image 8
image 9
image 11

Strength of magnetic field is 0.125 Tesla. 

Problem 2

Find magnetic force experienced by a charge particle with 50coulomb charge moving with unit velocity at right angle to magnetic field of strength 2 tesla. 

Solution:

  We know that equation of magnetic force and magnetic field is  

image 117
image 10
image 7

So, force experienced by particle is 100 newtons. 

Frequently asked questions | FAQs 

Q. How magnetic field and magnetic force varies with each other?  

Ans: “The magnetic force F is directly proportional to the strength of magnetic field.” As magnetic field gets stronger, magnetic force also increase and vice versa. 

Q. At which point in magnetic field, the charge particle experiences strongest the magnetic force? 

Ans: Magnetic field lines enter through south pole of magnet and leaves from north pole. Due to this magnetic force can be experienced strongest at either of the pole in comparison with opposite pole. 

Q. Does magnetic field affect magnetic force? 

Ans: Force experienced by moving charge is different at different points in magnetic field.

Magnetic forces of attraction or repulsion caused by movement of electrically charged particles is responsible for electric motor and attraction of iron towards magnet like effects. Static charges experience electric field whereas electric field and magnetic field can be experiences among moving charges. This magnetic force among two moving charges can be understand as the effect on either charge by a magnetic field by other. 

Q. Why magnetic force is perpendicular to magnetic field? 

Ans: If two objects or entities are at right angle with each other that means they are perpendicular to each other.

Because magnetic (Lorentz) field is directly proportional to v x B, where v is velocity of moving charge and B is magnetic field strength. As we know, vector cross product is always at right angles to each other of the vector factors, the force is perpendicular to v. 

Q. Do magnetic force work?

Ans: Magnetic forces do not work. 

For if Q moves an amount dl= vdt, the work done is  

image 118

It happens because (B x v) is perpendicular to v, so (B x v).v= 0

“Magnetic forces may reverse the direction in which charges particle moves but cannot speed it up or slow it down.” 

Also Read:

11 Non Contact Force Examples: Exhaustive Insights And Facts

by
image 128 300x200 1

In physics, the term “non-contact force” is used to describe the force that a body may exert on another body without actually coming into physical touch with it.

Following is the list of non contact force examples that we can see in our surrounding.

Let’s take a closer look at each of the non contact force examples above.

Non contact force examples

Clothes from dryer:

You must have observed the static cling on clothes. This is because of the triboelectric effect which comes under electrostatic force and is  type of non contact force. Triboelectric effect causes the static charge on your dryer’s clothing to become negative as various materials with varying affinities for electrons tumble together. This causes materials with a stronger affinity for electrons to lose electrons and become positively charged.

For a period of time while the clothes are drying, the initially humid environment provides a relatively conductive electrical path for static electricity to dissipate. However, as the clothes dry and the relative humidity in the dryer drum falls to extremely low levels, the air in the drum becomes highly resistive, causing the static charges generated by the dryer’s tumbling action to accumulate more quickly than they can be dispersed.

Sugar in plastic jar:

Sugar is the most prevalent component in every kitchen, and we all have a lot of it. If you look at the sugar that is kept in a plastic jar, and if that plastic jar is transparent, you may notice that the sugar has adhered to the inside of the plastic jar. This occurs as a result of the electrostatic force that is formed between the plastic jar and the sugar crystals. Herein the case, this electrostatic force is simply a non contact force.

Attraction of paper pieces on comb:

This is one of the most straightforward, but effective, noncontact force examples. Aside from that, this is one of the most typical demonstrations used in schools to demonstrate how static electricity is produced. When we rub the comb or balloon on our hair and then bring it close to the little bits of paper, we can see that the paper pieces are drawn to the comb or balloon and disappear. This demonstrates that a non-contact force, in the form of electrostatic force, is there.

Solar system:

We all are familiar with the words ‘Solar system’.  The gravitational force of the sun draws the planet toward it, causing the straight line of direction to transform into a curved line. Consequently, the planet continues to move in an orbit around the sun. In our solar system, the sun’s gravitational pull causes all of the planets to rotate around it. This force so called gravitational force is a form of non-contact force that acts between the sun and the other planets of the solar system.

non contact force examples
Solar System

Image Credits: “Solar System” (CC BY 2.0) by NASA Universe

Throwing ball:

While playing on the ground with ball we often throw the ball in order to pass it to another person. When we do so, then after reaching to certain height the ball falls back on the ground. The ball is falling to the ground as a result of the gravitational pull of the earth acting on the ball during its flight. This gravitational force between the ball and the ground is a type of non contact force which pulls the ball in downward direction.

Leaf fall:

In the autumn season, we usually observe the falling of faded leaves. When the tree’s leaves fall, they always falls on the ground or surface of the earth. This fall is simply because of the gravitational force which is a type of non contact force, acting between the leaves and the ground or surface of the earth. Earths gravitational force always attracts the bodies towards it. Leaf fall is the best and common non contact force example.

image 129
Leaf Fall

Image Credits: Image by  Mabel Amber, who will one day from Pixabay 

Roller coaster ride:

An amusement part is incomplete without the roller coaster ride. Roller coaster ride need some applied force through the form of electrical motor to reach up to certain height. After reaching that height, roller coaster is set free to work on the gravitational force alone. This working of roller coaster with gravitational force is simply a non contact force.

A door catch:

When it comes to kitchen cabinets or other types of cabinets and the doors, a magnetic catch is typically employed to keep the door closed. The working of door catch is efficient than the other traditional latches. Here, the working of magnetic force shows the type of non contact force.

Magnetic levitation trains:

Magnetic levitation trains also called as maglev trains worked on the powerful electromagnets. The fundamental principles of magnetism are used to make these trains float over guideways, rather than the traditional steel wheel and track locomotives. Because there is no friction between the rails, these trains may run at speeds of hundreds of miles per hour or more. But speed isn’t the only benefit of maglev trains. Because the trains hardly (if ever) touch the track, there is far less noise and vibration.

Maglev trains are less vulnerable to weather-related delays due to reduced vibration and friction. As a key contrast between them and conventional trains, magnetic levitation trains (maglev trains) do not have an engine, at least not the type used to accelerate standard train carriages over steel tracks. It functions only on the basis of magnetic force, which is a form of non-contact force.

image 131
Magnetic Levitation (Maglev) Train

Image Credits: Andreas Krebs., Shanghai maglev train, CC BY-SA 2.0

Attraction of iron pins:

Iron is a magnetic material, and iron pins are created from it. Magnets are attracted to iron because of the impact of their magnetic field on the iron’s magnetic properties. The iron pins stick to each other below the pole of a magnet because the magnet creates magnetism in the iron pins, which is attracted to the magnet and clings to it as a result of the magnetism.

By magnetic induction, the magnetised pins magnetise and attract the other pins in the vicinity of the magnetised pins. Therefore this magnetization and attraction of an iron pins becomes a non contact force example.

Navigation compass:

You must have seen the navigation compass which works on magnetism. The red pointer on a compass is actually a magnet, and it is being drawn to the Earth’s natural magnetism, which is referred to as the geomagnetic field. The Earth operates like a huge bar magnet, with one pole located in the Arctic (near the north pole) and another located in Antarctica (near the south pole).

For example, if the needle in your magnetic compass is pointed north, this indicates that it is being pulled (attracted) toward anything near the Earth’s north pole. Since opposite poles attract, your compass must be drawn to a magnetic south pole. That is, the magnetic north pole of Earth is really the magnet’s south pole. So this becomes one of the good non contact force example.

image 132
Navigation Compass

Image Credits: Image by PDPics from Pixabay 

Raindrops falling on the ground:

We all enjoy the rainy season. Because of the force of gravity, raindrops and all other falling items are pulled to the surface of the Earth. This action of gravity is simply a type of non contact force. However, the procedure that raindrops travel through in order to arrive at the place where they fall is a little more complex than a basic gravitational impact alone.

In order to produce rain, water must first become a gas, rise into the atmosphere, and then return to a liquid state again. The droplets subsequently yield to gravity and fall from the clouds. The hydrologic cycle is the collective term for the process through which water turns into rain and falls.

image 133
Rain drops falling on the surface of the earth

Image Credits: Veereshbmsce, Rain drop splash!!, CC BY-SA 4.0

These all are the non contact force examples that occurs in our surrounding.

Frequently Asked Questions (FAQ’s):

Q. What do you mean by non contact force?

Ans:  Non contact means no physical contact.

The force that a body may exert on another body without ever coming into physical contact with it is referred to as non contact force.

Q. What are the different types of non contact force?

Ans: There are four types of non contact force as follow.

Electrostatic force: Electrostatic force is the force that arises between two charged objects when they come into contact. Everything is composed of microscopic positive, negative, and neutral particles; opposite charges attract one another and similar charges repel one another; this is the consequence of electrostatic forces acting on the particles.

Gravitational force: There is a gravitational pull between all objects that have mass in them. It is a universal force that pulls items in the direction of one another. Everything is drawn toward the centre of the Earth by the gravitational attraction of the Earth’s gravity.

Magnetic force: When two magnetic fields come into contact with each other, they create magnetic force. Magnetic forces can be either pull (attraction) or push (repulsion) forces, depending on the type of moving charge on a metal object.

Nuclear force: Nuclear force is classified into two types: strong nuclear force and weak nuclear force. In a nucleus, there is a short-distance force called the strong nuclear force, which occurs between basic particles. It is not affected by charge and may be used between protons and protons, neutrons and neutrons, and protons and neutrons, among other situations. When a neutron decay takes place, the weak nuclear force is responsible for mediating the process, which results in the production of a charged particle and an uncharged particle known as a neutrino.

Q. State the difference between contact force and non contact force.

Ans: The following table illustrates the difference between contact force and non contact force.

Contact force Non contact force
This force is only produced when two separate things come into touch with one another. If there is no contact between the two items, then a non-contact force is produced by either attraction or repulsion between the two things.
The field and the contact force have no connection or physical contact to one another. The presence of non-contact force is usually accompanied by the presence of a different types of the field.
Contact forces are classified into the following categories: applied force, spring force, normal force, air resistance force, frictional force, and buoyance force. Other than contact force, there are other sorts of non-contact forces. These include electrostatic force, gravitational force, magnetic force, and nuclear force.
The contact force examples are glass of water on the table, hovering mouse, bungee jumping, suspension bridge, airplane in the sky, wooden block floating in water, sliding in playground, jar opening etc. Non contact force examples are throwing a ball, solar system, attraction of iron pins, attraction of paper pieces to hair comb, leaf fall, magnetic levitation train, roller coaster ride etc.
Contact force and Non contact force

Also Read:

How To Find Tangential Force: Several Approaches And Problem Examples

by

Understanding tangential force is essential in various fields such as physics, engineering, and mechanics. tangential force refers to the force that acts tangentially to an object’s circular path. In this blog post, we will explore how to calculate tangential force, its relationship with tangential speed, its significance in gear mechanics, its association with radius and tension force, and its role in circular motion. Let’s dive in!

III. How to Calculate Tangential Force

A. The Formula for Calculating Tangential Force

The formula for calculating tangential force depends on the specific scenario. In general, tangential force can be calculated using the following formula:

F_t = m \cdot a_t

Where:
– (F_t) represents the tangential force
– (m) denotes the mass of the object
– (a_t) refers to the tangential acceleration

B. Step-by-Step Guide to Calculating Tangential Force

To calculate tangential force, follow these steps:

  1. Determine the object’s mass (m).
  2. Find the tangential acceleration (a_t) by using appropriate formulas for the given scenario.
  3. Multiply the mass (m) by the tangential acceleration (a_t) to obtain the tangential force (F_t).

C. Worked Out Example: Calculating Tangential Force

Let’s consider an example to better understand the calculation of tangential force. Suppose we have a particle with a mass of 2 kg and a tangential acceleration of 3 m/s^2. To find the tangential force, we can use the formula:

F_t = m \cdot a_t

Substituting the given values, we get:

F_t = 2 \, \text{kg} \cdot 3 \, \text{m/s}^2

Simplifying the equation, we find that the tangential force (F_t) is equal to 6 N.

IV. The Interplay between Tangential Force and Tangential Speed

A. Understanding Tangential Speed

Before delving into the relationship between tangential force and tangential speed, let’s first understand tangential speed. tangential speed refers to the linear speed of an object moving in a circular path. It is measured in meters per second (m/s) and represents the rate at which the object covers the circumference of the circle.

B. How Tangential Force Influences Tangential Speed

tangential force has a significant impact on tangential speed. According to Newton’s second law of motion, the net force acting on an object is directly proportional to its acceleration. Therefore, the tangential force acting on an object influences its tangential acceleration, which, in turn, affects its tangential speed.

C. Worked Out Example: Finding Tangential Speed with Tangential Force

Suppose we have an object with a tangential force of 10 N and a mass of 5 kg. To find the tangential speed, we can use the formula:

F_t = m \cdot a_t

Rearranging the formula to solve for the tangential acceleration (a_t), we get:

a_t = \frac{F_t}{m}

Substituting the given values, we have:

a_t = \frac{10 \, \text{N}}{5 \, \text{kg}}

Simplifying the equation, we find that the tangential acceleration (a_t) is equal to 2 m/s^2.

Since tangential acceleration (a_t) is the rate at which the tangential speed changes, we can conclude that the object’s tangential speed will increase or decrease by 2 m/s in each second, depending on the direction of the force.

V. Tangential Force in Gear Mechanics

how to find tangential force
Image by Ilevanat – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

A. The Role of Tangential Force in Gear Operation

In gear mechanics, tangential force plays a crucial role in transmitting power and torque between gears. When two gears mesh, the tangential force acting on the teeth causes them to rotate and transfer rotational motion from one gear to another. The magnitude of the tangential force determines the effectiveness of power transmission and influences the gear system’s overall efficiency.

B. How to Calculate Tangential Force in Gear

To calculate tangential force in gear mechanics, follow these steps:

  1. Determine the torque exerted on the gear.
  2. Find the radius of the gear.
  3. Use the formula (F_t = frac{T}{r}), where (F_t) represents the tangential force, (T) denotes the torque, and (r) refers to the radius.

C. Worked Out Example: Calculating Tangential Force in Gear

Let’s consider an example to illustrate the calculation of tangential force in gear mechanics. Suppose we have a gear with a torque of 50 Nm and a radius of 0.1 meters. To find the tangential force, we can use the formula:

F_t = \frac{T}{r}

Substituting the given values, we get:

F_t = \frac{50 \, \text{Nm}}{0.1 \, \text{m}}

Simplifying the equation, we find that the tangential force (F_t) is equal to 500 N.

VI. Tangential Force and Radius: A Crucial Relationship

A. Does Tangential Velocity Change with Radius?

Yes, tangential velocity changes with radius. tangential velocity refers to the linear velocity of an object moving in a circular path. It depends on the object’s angular velocity and the radius of its circular path. As the radius increases, the tangential velocity also increases, assuming a constant angular velocity. Similarly, as the radius decreases, the tangential velocity decreases.

B. How to Find Tangential Velocity with Radius

To find the tangential velocity with radius, use the formula:

v_t = \omega \cdot r

Where:
– (v_t) represents the tangential velocity
– (omega) denotes the angular velocity
– (r) refers to the radius

C. Worked Out Example: Finding Tangential Velocity with Radius

Suppose we have a particle moving in a circular path with an angular velocity of 2 rad/s and a radius of 3 meters. To find the tangential velocity, we can use the formula:

v_t = \omega \cdot r

Substituting the given values, we get:

v_t = 2 \, \text{rad/s} \cdot 3 \, \text{m}

Simplifying the equation, we find that the tangential velocity (v_t) is equal to 6 m/s.

VII. Tangential Force and Tension Force: A Comparative Study

A. Understanding Tension Force

Tension force refers to the force exerted by a string, cable, or rope when it is pulled at both ends. It acts tangentially to the string’s length and is directed along the string. Tension force is responsible for transmitting forces and maintaining the equilibrium of objects connected by the string.

B. How to Calculate Tension Force

To calculate tension force, consider the forces acting on the object connected by the string. Use Newton’s second law of motion to set up equations based on the forces involved and solve for tension force.

C. Comparing Tangential Force and Tension Force

While tangential force acts tangentially to an object’s circular path, tension force acts along a string or cable. tangential force is responsible for the object’s circular motion, while tension force is responsible for transmitting forces through the string. Both forces play crucial roles in various scenarios and are essential for understanding different aspects of motion and equilibrium.

VIII. Tangential Force in Circular Motion: A Detailed Analysis

A. The Formula for Tangential Force in Circular Motion

The formula for tangential force in circular motion can be derived from the relationship between tangential force, mass, and tangential acceleration. It is given by the formula:

F_t = m \cdot a_t

B. How to Calculate Tangential Force in Circular Motion

To calculate tangential force in circular motion, follow these steps:

  1. Determine the mass of the object (m).
  2. Find the tangential acceleration (a_t) using appropriate formulas for circular motion.
  3. Multiply the mass (m) by the tangential acceleration (a_t) to obtain the tangential force (F_t).

C. Worked Out Example: Calculating Tangential Force in Circular Motion

Let’s consider an example to illustrate the calculation of tangential force in circular motion. Suppose we have a car moving in a circular path with a mass of 1000 kg and a tangential acceleration of 5 m/s^2. To find the tangential force, we can use the formula:

F_t = m \cdot a_t

Substituting the given values, we get:

F_t = 1000 \, \text{kg} \cdot 5 \, \text{m/s}^2

Simplifying the equation, we find that the tangential force (F_t) is equal to 5000 N.

IX. Tangential Force and Tangential Distance: An In-depth Look

how to find tangential force
Image by PatDob23 – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

A. Understanding Tangential Distance

Tangential distance refers to the distance covered by an object along its circular path. It represents the length of the arc formed by the object’s circular motion. Tangential distance depends on the radius of the circular path and the angle subtended by the arc.

B. How to Calculate Tangential Distance

To calculate tangential distance, use the formula:

d_t = r \cdot \theta

Where:
– (d_t) represents the tangential distance
– (r) denotes the radius of the circular path
– (theta) refers to the angle subtended by the arc

C. Worked Out Example: Finding Tangential Distance with Tangential Force

Suppose we have an object moving along a circular path with a radius of 2 meters and an angle of 60 degrees. To find the tangential distance, we can use the formula:

d_t = r \cdot \theta

Substituting the given values, we get:

d_t = 2 \, \text{m} \cdot 60^\circ

Simplifying the equation, we find that the tangential distance (d_t) is equal to 120 meters.

Also Read: