Physics

The drag coefficient is a dimensionless physical quantity influenced by the various parameters that can be affected by the motion in the fluid medium.

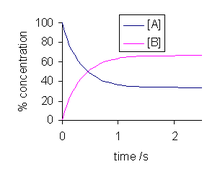
In the study of fluid mechanics, the drag coefficient plays a vital role as it resists the motion of the solid object in the fluid medium. This drag coefficient depends on velocity, the object’s cross-sectional area, and density. Is the drag coefficient constant if the parameter mentioned above varies?

We are trying to answer the above equation in this post. Let us discuss how and when is drag coefficient constant and the facts related to the constant drag coefficient below section.

The drag coefficient is directly influenced by the velocity of the flow of the object in the fluid. If the velocity is kept constant over a period, there may be a change in the drag, but the drag coefficient is constant as it is the dimensionless quantity.

C_D=2F_D/ρv²A

From the above formula, if we consider the object motion in the fluid, the terms F_D, ρ, and A are constant for the same object; thus, only possible changes in the velocity we can write the above equation as

C_D=Constant/v²

Thus the change in velocity inversely corresponds to the drag coefficient.

How does drag coefficient vary?

Some factors like air resistance, shape and geometry of the object affect the drag coefficient. But the variation of the drag coefficient completely depends on the velocity of the object in the fluid.

The square of the velocity of the object is proportional to the drag coefficient of the object in fluid surroundings. The drag coefficient varies with the square of the relative velocity of the object.

Consider the aerodynamic drag; if the velocity of the object increases to its square value, the drag coefficient falls down at the same value. Thus at a higher velocity, the drag coefficient is less, giving the better performance. So it is clear that increase in velocity, the drag coefficient decreases.

When does drag coefficient vary?

In most cases, the drag coefficient varies with velocity inversely. But other than the velocity, there are several factors responsible for the variation of the drag coefficient. Some of them are listed below:

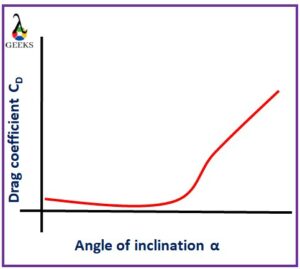
• The angle of object – The factors angle of inclination of the object in the fluid surface is one reason for the variation of the drag coefficient. When the angle of attack is smaller, the drag coefficient is lower.

• The density of the medium – If the object is low from one medium to another medium of different densities, the drag coefficient varies for the same object. Consider that object is moving from air to water; the density of the air and water is different from one another. Thus the drag force offered to the object changes, thus varying the drag coefficient.
• Another necessary consequence of vary in drag coefficient is the type of flow. When the airflow or hydraulic flow is turbulent at a higher velocity, variation in the drag coefficient will occur.
• Cross-sectional area –The reference area of the object’s cross-section influences the drag force. If the area of the object is doubled, the drag force is also doubled. Thus varying the drag force causes the proportionate change in the drag coefficient.

D=A_ref×constant; where A_ref is the area of reference.

When is drag coefficient constant?

In most cases, the constant drag coefficient is referred to as the constant velocity –that means if the velocity of the object on the fluid medium is kept constant, the drag coefficient would also remain constant.

However, the constant drag coefficient depends on the Reynolds number too. As long as the Reynolds number is constant for the object flow, the drag coefficient remains constant.

One fact we need to observe here is the Reynolds number of the object motion in the fluid medium is also depends on the entities like speed, density and viscosity of the medium. Thus constant drag coefficient is associated with the terms involved to describe the motion of the body in the fluid environment.

Frequently Asked Questions

What happens when an object possesses a high drag coefficient?

The low or high value of the drag coefficient directly impacts the motion of the object in the fluid.

If an object possesses a higher drag coefficient, the object might be a flat plate whose ability to move in the fluid surface is relatively slow. The object with a high drag coefficient exhibits significant resistance to the motion.

What is meant by Reynolds number?

In fluid mechanics, the Reynolds number describes the flow pattern of the object in different fluids.

Reynolds number can be defined as the dimensionless number given by the ratio of inertial force over the viscous force of the fluid. The Reynolds number helps to categorize the flow of the fluid system as the turbulent, streamlined, or laminar flow.

Can the drag coefficient of a body be greater than 1?

The value of the drag coefficient depends on the nature of the flow such as streamline or turbulent flow.

If two objects of the same area of cross-section move with the same velocity may have different drag coefficients. The drag coefficient for a streamlined body is always less than 1, whereas, for un-streamlined bodies, the drag coefficient value can be 1 or more than 1.

Does the size of the object affect the drag coefficient?

The drag coefficient and the size of the object correlated to one another. Objects of different sizes possess different viscous and inertial forces responsible for the drag force.

The different viscous and inertial force refers to the different Reynolds number; this means that the size of the object refers to a change in the Reynolds number. So it is clear that the size of the object influences the drag coefficient to several extent.

Does the drag coefficient depend on the altitude?

Drag coefficient is independent of the height. The increase or decrease in the altitude does not make any impact on the drag coefficient.

In some cases, as the altitude increases, the Reynolds number may change; thus, there will be a change in the drag coefficient. But if the Reynolds number remain unchanged even if the altitude changes, the drag coefficient is unaffected by the altitude.

Also Read:

• Factors affecting solubility
• Is deceleration negative
• Example of reversible change
• Types of pulley
• Buoyancy examples
• Is calcium malleable
• Physical irreversible change example
• Mercury formation structure and facts
• Hammer drill for concrete
• Neutral equilibrium example

This article focuses on dynamic equilibrium example. We have an idea of what equilibrium is, we will read in detail about its type- Dynamic equilibrium in this article.

The word dynamic refers to something which is having mobility. And equilibrium is related to stability and balance. We can say that dynamic equilibrium refers to something which is mobile and stable. We will study further about dynamic equilibrium in this article.

• Dissociation of acetic acid in an aqueous solution.
• Train running with constant speed
• Aeroplane flying at constant speed
• Car moving at constant velocity
• Running on a treadmill at constant speed
• Free falling body after it has achieved terminal velocity
• Number of cars entering and leaving the city at the same rate
• A steady flow of water in pipe
• Heat transfer in heat exchanger
• Rectilinear motion of bodies

What is dynamic equilibrium?

In Physics/Chemistry, dynamic equilibrium occurs in a reversible chemical reaction. In this type of reaction, the formation of both reactants and products occurs at same rate. In a nutshell, backward and forward reaction occur at same rates.

Hence, the net content of both reactants and products remain same. This is also called as steady state sometimes. Thus we can say that things are dynamic in nature but has a balance too. In thermodynamics, this is called as thermodynamic equilibrium where reactions occur at such a rate that composition of mixture does not change significantly.

Dynamic equilibrium example

We know the meaning of dynamic equilibrium. There are various places where we can see dynamic equilibrium taking place in our every day lives. Lets get a clearer idea of what exactly dynamic equilibrium is by looking at its examples.

Dissociation of acetic acid in an aqueous solution

Rate of formation of reactants is equal to  rate of formation of products hence the net content of the system is same. This is why it is said to be in neutral equilibrium.

Image credits: Wikipedia

Train running with constant speed

When the train running with constant speed, the friction is balanced with the forward force applied by the train. At constant velocity, the magnitude of forces are not changed.

Aeroplane flying at constant speed

The upthrust is equal to the force due to gravity. No other change is observed hence it is dynamic equilibrium.

Car moving at constant velocity

The weight is balanced by reaction force and forward force is balanced by friction. Also the forward force is opposed by friction with equal rate. No other change in force is observed. The net force remains the same hence it is said to be in dynamic equilibrium.

Running on a treadmill at constant speed

The forward movement of legs is equal to the backward movement of treadmill floor leaving the human running at the same place hence these forces balance each other and makes the person running on the treadmill and the treadmill itself are in dynamic equilibrium. (Considering both as one system).

Free falling body after it has achieved terminal velocity

After achieving terminal velocity, all the forces are balanced and do not change even with downward movement of the free falling object.

Number of cars entering and leaving the city at the same rate

Particles entering and leaving the system at the same rate is an example of dynamic equilibrium. Here the number of cars entering and leaving the city are same. Considering city as a system, the city is in dynamic equilibrium.

A steady flow of water in pipe

The rate at which water is entering the pipe is equal to the rate at which water is leaving the pipe. Hence the pipe as a system is in dynamic equilibrium.

Heat transfer in heat exchanger

The heat absorbed by the cold fluid is equal to the heat left by the hotter fluid. Hence the pipes of heat exchanger in terms of heat transfer is in dynamic equilibrium. If we look at the mass flow rates at inlet and outlet and they both are same, we can say that entire heat exchanger is in dynamic equilibrium.

Rectilinear motion of bodies

Like trains and cars, their rectilinear motion makes them in dynamic equilibrium. In rectilinear motion having constant velocity, the net forces acting in the system remain same so the system is in dynamic equilibrium.

Difference between static equilibrium and dynamic equilibrium

The major difference between both these equilibriums is the mobility of particles/objects in the system.

In dynamic equilibrium, the rate of particles/objects entering the system is equal to the rate of particles/objects leaving the system. Here we can say the contents of this system are in continuous state of motion. In static equilibrium, the object is at rest and in equilibrium. This means there is no mobility of the contents in the system.

What is static equilibrium?

Static equilibrium is a state of equilibrium attained by bodies when they are at rest. In this case also, the sum of all forces acting on the body is zero.

If for example, an elephant is pulling one end of an inelastic rope in x direction and a truck is pulling other end in -x direction with the same magnitude of force, then the rope does not displace from its original position. This is the best example of static equilibrium.

Also Read:

• Bar magnet uses
• Effective focal length calculations
• Atmospheric dispersion correctors
• Uses of pulley
• How to find q factor
• Reduce friction
• Dew point and bubble point
• How to find static equilibrium
• Half mv 2 derivation
• Exothermic reaction 2

A compression is an act of applying force on the object that results in the reduction of volume and dimensions of the object.

The force has to equal and oppositely react on the object in order to be a compressive force. Here, is a list of example of compression that we are going to discuss in this article:-

Sponge

A sponge has pores that are filled with air molecules. On compressing the sponge, these air molecules are removed as the space between the gaps is reduced by compression.

Draining out Water from Wet Clothes

The wet clothes are compressed to drain out water from the clothes. On applying compression force the volume of water is reduced from the cloth.

Compression of Bed Mattress

If you have noticed, that on sitting on the bed mattress, or keeping any load, the area of the mattress underneath and near the surrounding gets compressed.

Your body weight is imposed on the mattress and an equal and opposite force is reacting from down that is resisting the force due to weight.

Read more on Negative Tension:What,Why,When,Examples,How To Find.

Deposition of Sediments

The sediments are carried by the river streams and are deposited in the basin while making a fall from the cliffs.

The sediments underneath the stack of sediments go under compression due to overlying weight. These grains are compressed and the sedimentary rocks are formed.

Compression of Spring

Spring is an elastic item that on compression built enough potential energy which is then converted into tremendous kinetic energy on releasing the pressure. On compression, the length of the spring is decreased.

Hydraulic compression

Hydro means water. Any object underwater goes under hydraulic pressure. The pressure acting on the object from all the dimensions results in the compression of the object. Hence is called hydraulic pressure.

Condensation

Condensation is also a phenomenon of compression. The water vapours scattered around the area are condensed into a cloud, thus reducing the area of water vapours. The water molecules go under compressive force to condense into a cloud.

Laddoo

While preparing laddoo we compress the mixture together to hold it tight.

Read more on Tension Between Two Blocks: Several Entities And Problem Examples.

Air Conditioner

The air conditioner has a compressor that compresses the low pressure air to the high pressure air cooling it down, which is then travels to the condenser and turns into liquid under high pressure only.

This liquid is then transferred to the evaporator, where it takes the heat to convert liquid back into the air, and the cool air is released back into the room.

Himalayan Mountains

The two plates on the asthenosphere attracting towards each other are called constructive plates.

Upon joining the plates together and compressing further, the mountains are developed in consequences. The Great Himalayan Mountains is an example of such constructive plates when the Indian plate met the Asian plate.

Jumping Shoes

This shoe comes with a spring underneath the shoe that helps to take a long leap, hence called jumping shoes. On application of the force on the spring due to body weight, the spring is compressed, the potential energy is built in the spring and that is converted into kinetic energy and is given off on a jump.

Mud balls

When two balls collapse together, both the balls compress due to the force imposed from the opposite direction. The shape of the mud balls changes as they are not elastic bodies, they are deformed on compression.

Read more on Does Viscosity Change With Pressure: Exhaustive Insights.

Filling the Sugar Containers Tightly

Container tightly filled by filling all the gaps within, the sugar inside the containers feels the pressure from the walls of the container from all sides.

The density of the sugar per unit cross-sectional area increases on tightly filling the container. The sugar in the lower part of the container is compressed more than the overlying volume.

Packing Clothes in the Suitcase Tightly

If you want to pack lots of clothes in a single suitcase, then you compress the clothes to zip them inside the suitcase in order to get all the clothes packed. The compressive force is acted from all sides of the suitcase and equal force is acting outward.

Rolling a Chapatti

While rolling a chapatti you are actually compressing the dough to roll it into a thin layered chapatti.

Rubber Ball

A rubber ball is an elastic item that on compression reduces its size. If you place the ball on the ground and apply pressure on it, the equal and opposite force will act on the ball on its other side from the ground, hence the rubber ball will compress.

Squeezing

To squeeze anything like lemon, orange, etc. we apply a force from two opposite directions called compression to squeeze out the juice from it.

The volume of juice from the lemon is reduced on compression.

Road Rollers

A road roller is a vehicle designed to compact the soil, gravel, and concrete for the construction of the road.

On rolling the surface with the rollers, the soil or concrete is compressed, thus giving a solid and a rigid metallic road.

Read more on Frictionless Surface Acceleration: Exhaustive Insight and Facts.

Mortar and Pestle

A mortar and pestle are used for grinding the spices, herbs, nuts, etc into fine particles. The pestle puts a force on the mortal and the equal force is acting on the area to resist this force thus causing compression of the food item encountering in between the portal and pestle which can’t resist this force and gets crushed into finer particles.

Gym Ball

A gym ball is used for balancing exercises. If you put palm pressure on the ball, then the compression force will be experienced on the gym ball showing its impression on putting a force. The air inside the ball is compressed due to this force.

Longitudinal Waves

The longitudinal waves propagate in the direction of motion of the vibrating particles and thus producing the region of compression and rarefaction. In the region of compression, the density of the waves is high and appears as a compaction of the waves.

Pump

On pulling the piston the air is filled in the gap created in the chamber by opening the inlet. While pushing the piston down, this inlet gets close and no air can escape from the chamber, due to which the air is compressed and is pumped.

Bridges

The bridges undergo compression when the heavy load approaches bridges.

The tension is generated across the length of the bridge structure between the poles of the bridge adds to the compression strength to withstand compression. This compression may result in cracks on the bridges.

Shoe Soles

The entire body weight is exerted on the shoe soles while walking, running, jumping, due to which the shoe soles undergo compression that further leads to warping of soles.

Frequently Asked Questions

What is compressive stress?

A stress the restoring force acting in the object that resists the external imposing force.

The compressive stress is a restoring force acting in opposition to the force applied on the object that results in the deformation of the object reducing its volume and dimensions.

What is compression strength?

Compression strength is the ability of the material to resist compression.

On application of the compression force, the stress is built inside the object. The object will deform if the strength of the object is very less to resist this levied force.

What is the SI unit of compression?

The formula to measure a compression is F(c)=ma.

The compression is the force on the object from two or more directions, and hence the SI unit of compression is Newton.

Why does the object get deformed on compression?

The compression of the object results due to the action of forces from different dimensions.

If the compressive strength of the object is not enough to resist the compressive strain then the object will be deformed.

Also Read:

• Dynamic equilibrium vs static equilibrium
• Static equilibrium examples
• Ozone generator ozonator
• Robot welding types characteristics
• Rolling friction and sliding friction
• P polarized
• S polarized
• Doppler effect for moving observer
• Stable equilibrium example
• Is sliding friction static

Constructive interference example in the real world will allow us to understand what happens in the micro-level of physics.

When two waves having the same amplitudes interfere with each other, they will have the resultant wave displace in the same medium with the equivalent amplitude as the original ones. Let us see a few constructive interference example and understand the process of the interference.

• Interference of Colors
• Single Slit Diffraction
• Young’s Double Slit Experiment
• Water Pool
• Speakers
• Musical Instruments

Interference of Colors

Interference in itself is one of the constructive interference example. Let us see how this works. Firstly what is interference? It is the co-joint of two waves that into contact with each other.

Waves can exist in all forms, namely light, sound and electromagnetic. Waves are made up of two different factors known as the crest and trough; here, the crest means the top node of the wave and the trough is the down node of the wave.

These top and down nodes of a wave make a big difference when two of such waves go hand in hand with each other. Say when these waves meet, they interfere, meaning internally, they are in phase with one another.

When the top nodes of one wave meet another, that is, the crests of two waves meeting one another are termed as constructive interference. Now let us see how this concept works well in terms of colors when considered.

Bubble colors are said to be one of the constructive interference examples. There are different colors that come under constructive interference. Namely yellow and magenta, where their crests meet another crest and form a wave pattern.

Let me also tell you that diffraction is the after effect of the interference phenomena. Where the colors generally are deflected at various different angles so finally form a final image. They interfere with each other, so we get a new pattern of waves, sometimes different colors too.

Single Slit Diffraction

Well, one can ask what single slit diffraction has to do with constructive interference example. Actually, it does, if not in the process the definitely in the end product.

The single slit experiment is to show how light waves bend around the corner of any target surface and how well it forms a resultant wave pattern in the same medium or rather a different one.

When we allow the light to enter a slit of the dimension that corresponds to the wavelength of the light been allowed to pass through, now when a ray of light passes through the slit, the light undergoes diffraction and appears as a new type of wavelet.

Now how does this become a constructive interference example? The resultant wave will depict whether the wave has been constructive or destructive in nature. The angle at which the light has been displaced in a new position will actually tell about the type of interference.

The wave after hitting the target will be allowed to propagate in a specific direction so that the wavefront is formed accordingly. The waves coming out of the slit will interfere with each other in no time.

If the wave increases in a particular way, then we need to know that it is a constructive interference so that we get to see a beam of light in the process.

Young’s Double Slit Experiment

The experiment is more or less connected to the single-slit experiment. There it was just a single slit, but in this experiment, we see double openings for the light waves to propagate.

The experiment also deals with bringing out the true nature of light, whether it is a particle or a wave. Indeed it seems to be a wave since it gives a beam in the end result.

So it can also be under the category of constructive interference examples where the resultant wave adds up with each other creating large waves altogether. Their amplitude is the same since the top and down nodes meet each other.

Depending upon the type of wave pattern is made when the light wave hits the slits, we decide whether the interference is constructive or destructive. So the angle at which the light wave hits the slit makes a significant impact on the resultant pattern of the wave.

The angle at which the light wave hit the target is supposedly taken into account. The reason is when it comes out as a wavefront in which the angle and the number of waves present will decide the type of interference.

Water Pool

The water pool is one of the best ways to understand the interference pattern, and also it is an easy constructive interference example. So this is considered as an experiment in some instances to understand the interference concept better.

For example, consider a person standing inside the pool and striking both hands back and forth. So it will definitely make wave patterns. So when the hands go front and back, the troughs, as in the waves, will cancel out inside.

The cancelling is termed to be destructive interference. And when the waves keep on adding up each other, then it is constructive interference. The reason is, as mentioned earlier, the nodes of both top and bottom will meet each other, and it will result in the wave pattern having amplitude with a more significant value.

The interference made by the wave will have a circular pattern, and they are regarded to be the wavefront, meaning, and the secondary wavelets that comes from the primary waves that mix with each other.

Here we see the constructive interference since the wave in the water pool is added with each other when the water is stroked by hand back and forth. The crest and crest of two waves basically meet at their nod points.

Speakers

Speakers are an excellent constructive interference example as they will ensure the sound waves have been heard by the listener when put out loud in a vast hall.

Basically, when there are two speakers kept in a hall and when they both are played together, then they are said to have a constructive interference pattern. The process goes like this, beginning the sound coming from both the speakers must be of the same amplitude.

The reason for the amplitude to be the same is that only then the sound is heard in the same measure. The crests of both the waves must be in such a way that they are equal and meet each other at the exact location.

When we consider the sound waves to have the same amplitude, then the waves have their respective nodes in a point where the tops and bottoms meet at the same point and are in phase. The frequency of the sound is also the same when it is connected to on single source, so there is not much loss of energy in such cases.

There are also possibilities for destructive interference when the waves do meet but end up cancelling out each other. That is when the crest of one wave is the bottom part of a wave meets the crest that is the top part of a wave, meeting one another at the same point.

Hence when the sound comes out of both, the speakers appear to be the same simply because they have the same amplitude and even when the wavelength and such factors affect the sound waves.

Musical Instruments

Musical instruments are a great way to explain the constructive interference example. They have sound waves that interfere with each other and give a result in the form of constructive or destructive.

Mainly string instruments contribute mainly to constructive interference. Let’s take guitar as an example for this concept. When we tune guitars in such a way that while it is played, we can hear a neat, pleasant tune and the reason is that constructive interference has occurred in the process of tuning.

The reason why mostly the strings instruments are being tuned is that when they are playing, we need to hear the sound, which is in phase and is cordial. The sound waves that resulting out of the played instrument arrange themselves in a pattern where there is no disturbance in the way it has been delivered.

The wave’s presence increases as it is played because they add up each other, and the amplitude is in such a way that it is more significant than the individual amplitude of the wave. So the crests of the wave’s present will undoubtedly team up at one point and the same, also the troughs too.

In this way, we can hear a piece of better music, and less amount of noise will be coming out of the instruments. And this is the main reason why the string instruments are always tuned before they are played.

Let us see how there are side effects present in such cases. There is something called the beat frequency. Sound is made up of several waves together, which has different frequencies, and when the entire wave meet each other, they either add up or cancel out. So we formally find a constructive interference pattern here.

Also Read:

• Mirror reflection examples
• S polarized vs p polarized
• Radioactive decay examples 2
• How to find coefficient of friction
• Dry friction example
• Table without friction
• A detailed overview on jupiter the largest planet
• Monochromatic aberration
• Longitudinal vs transverse
• Is impulse conserved

Constructive interference vs destructive interference is a more superficial comparison to understand the wave interaction.

CONSTRUCTIVE INTERFERENCE	DESTRUCTIVE INTERFERENCE
Two waves sum up each other	Two waves negate each other
Crest and crest meet one another	Crest and trough meet one another
The resultant wave has a larger amplitude	The resultant wave has a smaller amplitude

Now we shall see what factors aid in determining the difference between constructive interference and destructive interference.

• Constructive interference vs destructive interference considering Amplitude
• Constructive interference vs destructive interference considering Wave’s
• Constructive interference vs destructive interference considering Frequency

We must take note of the type of wave we must consider before they interfere with one another. Basically, when two waves interfere with each other, that process is termed to be interference.

When one wave interferes with another wave and results in a larger wavelength, it is termed constructive interference, and when two waves interfere with each other, resulting in a smaller wavelength, then it is termed destructive interference.

Generally, when in constructive interference, the two waves meeting each other with the same amplitude will result in the wave having an amplitude that is larger than the individual wave. This is mainly seen in speakers playing the same music, and we hear the same music but very much louder.

In destructive interference, the two waves which go hand in hand with each other will always have a resultant displaced wave having amplitude that is small. The crest of one wave meeting the trough of another cordially gives way for destructive interference.

We can see the destructive interference example in daily life. The destructive interference concept is applied in the technology level, that is, headphones being a noise canceler. The amplitude will be much smaller compared to that of constructive interference.

Constructive interference vs destructive interference considering Amplitude

The constructive interference is termed as such because the two waves meeting one another will have their respective amplitudes. When they encounter each other, the amplitudes of the two waves will merge and result in one single wave of equal amplitude.

The wave appearing in the same medium being a resultant has an amplitude that is way much higher. So, in this case, the medium in which the constructive interference occurs will have an upward displacement.

The resultant upward displacement of the resultant wave is larger than the individual displacement of the two waves interfering. The constructive interference occurs along with medium and in the same direction as the originating waves.

Let us take an example where the constructive interference is influenced by the amplitude. Consider two pulse waves travelling in the same medium also in the same direction. They will have particular amplitude individually.

In destructive interference, the waves having a 180⁰ phase will cancel out each other if the two are positive and negative. The individual amplitude value is larger than the final wave of amplitude that is way much smaller.

The waves interfering have nodes which are called the ends of the wave. The constructive and destructive have the nodes that match at the exact location, which is the resultant wave of the interference process.

Constructive interference vs destructive interference considering Wave’s

Wave patterns that appear in general are due to the consequence of interference of the two waves colliding with each other.

When the waves interfere, the resultant wave pattern appears in the same direction since the amplitude has the more significant measure. Here the crest and crest meet each other. But in destructive interference, the wave pattern appears opposite to each other.

The resultant wave pattern in a destructive interference will always have an opposite where the crest of one wave will meet the rough of the other wave. Also, the amplitude of the displaced wave will be smaller than the individual waves that interfere with each other.

Let us see how wave patterns are formed when the interference process takes place in a pool. When we stand inside the pool with both hands stretched and move back and forth, there will arise a wave pattern.

The wave pattern is simply the wavefronts of the primary waves when they undergo interference. When both hands have been stroked back and forth, it will form a wave pattern. The troughs in the wave pattern will cancel out each other.

The cancelling of the troughs of the wave is termed destructive interference. The area of the wave pattern which keeps on increasing is a sign of the addition of the waves. This is termed constructive interference.

These wave patterns are essential not only in water sound but mainly in light too. In light, when the light waves hit a surface that has a gap in it, the diffraction pattern is obtained. When one single beam enters the hole, it will come out as a whole set of waves.

Constructive interference vs destructive interference considering Frequency

Generally, constructive interference occurs when the crest and crest of two interfering waves meet each other. Due to this, the amplitudes also will add up and form a wave pattern of the same individual waves.

When the Frequency of the waves appear to be the same, then the resultant wave will be the same and appear in the same medium. When we consider the sound waves, the sound will be heard more in constructive interference.

When a number of cycles happen at a particular point given is certainly termed to be the frequency and it also related to amplitude of the resultant.

Hence when constructive interference vs destructive interference occurs, it will have so many factors that will influence the secondary wave pattern in general.

Frequently Asked Questions

What is the interference of light?

When the two light waves interfere with each other is termed light interference.

The disturbance of light due to one deformed wave will lead to the interaction of the two waves. Interference of light occurs if the light waves have the same amplitude, Frequency and also should be coherent.

What is the destructive interference example?

Noise-cancelling headphones are one of the prominent examples of destructive interference.

When the headphone has a microphone attachment, it will gradually pick up the Frequency of the waves of the incoming. So the amplitude will be less when the resultant wave is displaced in opposite to one another.

What is a good interference example?

One good example of sound wave interference is musical instruments.

For instance, let us consider guitar. When two guitars are tuned in phase, they will sound the same when played. But if the tuning is different, we get to hear different notes while hearing. When speakers play a sound, if they play with the same amplitude, then we call it constructive interference.  

Also Read:

• How do mirages form
• How to find coefficient of friction on an inclined plane
• Classical conditioning examples
• Conduction examples
• Do a hammer drill spin
• Properties of reflection
• Numerical problems on gravitation class 9
• Constructive and destructive interference
• How total internal reflection occurs
• Why is the sky blue