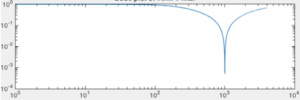
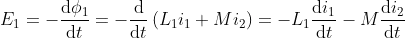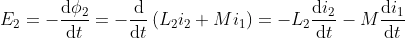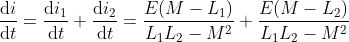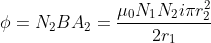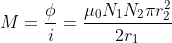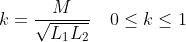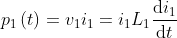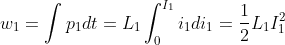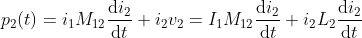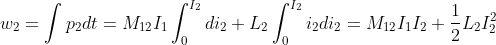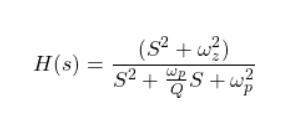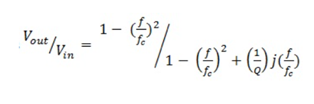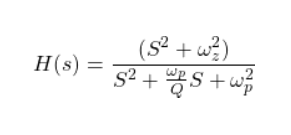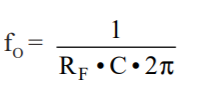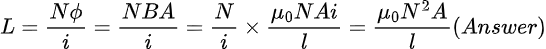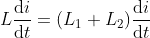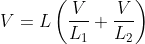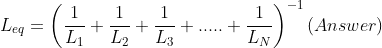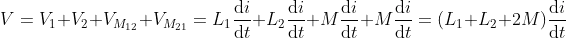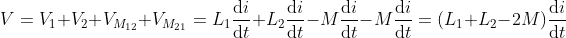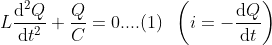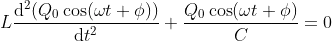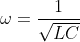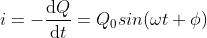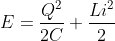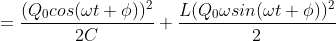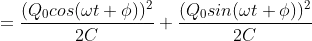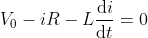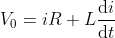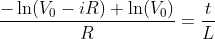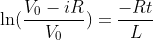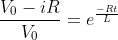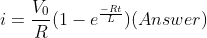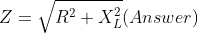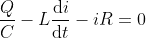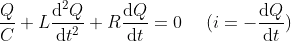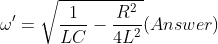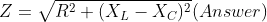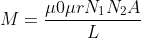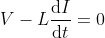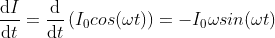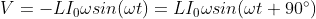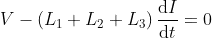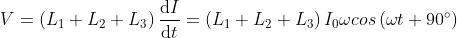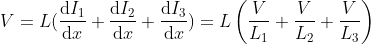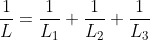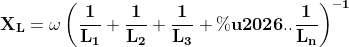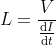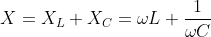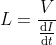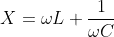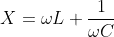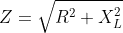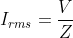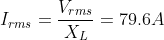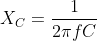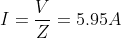What is current and voltage division?
Voltage and current divider
Current and voltage division are real-life examples of Kirchhoff’s laws. The current division takes place in a parallel circuit, while voltage division occurs in a series circuit.
What are the current divider rule and voltage divider rule?
Current divider rule | Current divider law
What is a current divider?
The current-divider rule is a practical application of Kirchhoff’s current law. It states that,
In a circuit with a parallel combination of resistors, the current gets divided into all the branches having the same voltage across them. Thus a parallel circuit behaves as a current divider.
What is Voltage divider with current source ?
Voltage divider current
A voltage divider with a current source divides the supply voltage in the resistances. The voltagedrop across any resistor is the multiplication of the resistances with the value of current in the circuitry.
Current divider circuit example
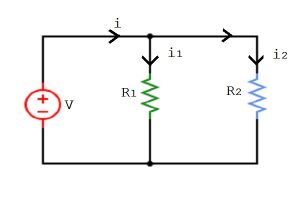
Let us take a circuit with a DC voltage source of V volt and two resistors R1 and R2, connected in parallel. The total current in the circuit is i, current through R1 is i1, and R2 is i2.
What is Current divider theory | Current divider rule definition | Current divider definition ?
Current divider theorem | Current divider principle
The current-divider rule says that the current in any branch of the parallel circuit is equal to the total current in the circuit multiplied by the ratio of the resistance of the opposite branch and the total circuit resistance.
Current divider rule derivation | Formula derivation
Current divider parallel
In the image1, we can see two parallelly connected resistances R1 and R2, are joined with a DC voltage V and currents thru them are i1 and i2, respectively.
The equivalent resistance of the circuit is





What is Voltage and current divider formula ?
Current divider rule formula
According to the currentdivider rule,
Current in through any resistor = Total current of the network x resistance of other resistor/equivalent resistance of the circuit.
Voltage divider rule
According to the voltage divider rule,
The voltage drop across any resistor = Total current of the network x resistance of that resistor
Current divider equation | Derive current divider equation
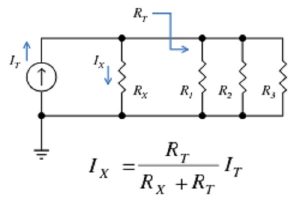
For the above circuit, we can see that resistances R1, R2, R3, and RX are connected in parallel. A voltage source is added to this combination, and current IT flows through the circuit. The equivalent resistance of R1, R2, and R3 is denoted as RT, and If the current across resistor RX is IX, we can say that,

What is Current divider rule for 2 resistors in parallelly connected ?
Parallel circuit current divider | Current divider formula for parallel circuit
Two resistors R1 and R2, are connected in parallel with a DC source V. If the currents i1 and i2 flow through them and the total current is I then,


What is the Current divider rule for 3 resistors in parallelly ?
Current divider rule for 3 resistors
Three resistors R1, R2, and R3, are connected in parallel with a voltage source V. Total current in the circuit is IT and branch currents are i1, i2, and i3, respectively. Therefore,


Current in a voltage divider
As the voltage dividers are series circuits, the current through all the resistors or impedance elements is the same. With the help of the total current, the voltage divider rule is constructed. The voltage drop across any resistor equals the total current multiplied by the resistance of that resistor present in the circuitry.
Current divider applications | Current divider examples
- The main purpose of using a current division is to reduce complexity while solving for current in any circuit. It divides the current into small components.
- Current division is used to protect circuits from overheating. As it divides the total current into fractions, small current components generate, and large current flow is avoided. This allows less heat dissipation and saves the circuits from any damage.
High current voltage divider
A voltage divider that can deliver a high amount of current is difficult to be built with a traditional resistor network. A switching regulator or a buck converter type design can come in handy in this case. For the buck converter approach, its voltage reference can be replaced with a divider derived from the incoming supply.
Series voltage divider with parallel load current
If a load resistance is connected with the voltage divider in parallel, the overall equivalent resistance decreases. Therefore the current in the circuit increases, but the voltage at the divider output drops.
AC current divider
AC circuits function the same as DC. Just the impedances must be written with their phasor representations using the complex quantity j.
Current divider impedance
If we generalize the resistive network equation for elements other than resistance,



Where IT is the total current, IX is the current through a particular branch, ZT is the equivalent impedance of the circuit, and ZX is the impedance of that branch.
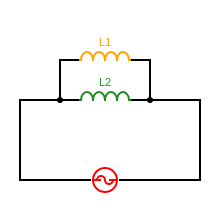
To know about Inductors in Series and Parallel click here
How to use the current divider rule? How to apply the current divider rule? | How to divide current in a parallel circuit?
Current divider method
The current division is calculated in the following steps:
- First, find the equivalent resistance RT of the other circuit elements, excluding the one for which current needs to be calculated (RX)
- Compute the fraction of this RT and RT + RX
- Multiplying this quantity with the total current would fetch the desired branch current IX.
What is the difference between voltage divider and current divider ?
Voltage divider and current divider | Current divider vs voltage divider
| Current Divider | Voltage Divider |
| It is constructed through parallel circuits. | It is constructed through series circuits. |
| The values of current through the resistors are measured. | The values of voltage drop through the resistors are measured. |
| The voltages in all the resistors are equal, the currents vary. | The currents in all the resistors are equal, the voltages vary. |
Low current voltage divider
Voltage divider circuits with low or almost zero current can be used to design switches with an additional transistor.
Voltage divider current limit
There’s no specific limit for current in a voltage divider. However, observed values suggest that currents over 1 amp can be regarded as high for the voltage dividers.
Current divider problems with solutions
Current and voltage divider
Q. Two impedances, Z1 = 2+j5 and Z2 = 5+j2, are connected in a parallel circuit. Total current, I = 10 amp. Using the current division, find out the currents through individual impedances.
We know,

Therefore, I1 = 10 x (5+j2)/ 2+j5+5+j2 = 5(7-j3)/7 amp
I2 = I – I1 = 10 – 5(7-j3)/7 = 5(7+j3)/7 amp
Current and voltage divider examples | current and voltage divider problems
Q. Three resistors of 6 ohm, 12 ohm, and 18 ohm are connected in series with DC supply voltage 54V, then calculate the voltage drop across all the resistors.
The voltage divider rule says that voltage drop across any resistor in a series circuit = resistance of that resistor x the current.
Now, equivalent resistance of the circuit = 6 + 12 + 18 = 36 ohm
So, net current in the circuit = 54/36 = 1.5 A
Therefore, voltage drop across 6 ohm resistor = 1.5 x 6 = 9 Volt
voltage drop across 12 ohm resistor = 1.5 x 12 = 18 Volt
voltage drop across 18 ohm resistor = 1.5 x 18 = 27 Volt
Current divider rule example problems | Current divider sample problems
Q. 4 resistors with resistances 5 ohm, 10 ohm, 15 ohm, and 20 ohm are connected in parallel with a voltage source. The total current in the circuit is 5A, then compute the current thru the 10Ω resistor.
The equivalent resistance of the circuit = 5 x 10 x 15 x 20 / (50 + 75 + 100 + 150 + 200 + 300) = 17.14 Ohm
Therefore, current through the 10 ohm resistor = 5 x 17.14/10 = 8.57 A
Q. Two resistors of 10 ohm and 20 ohm are connected in parallel with a 200 V DC supply, then compute current thru the 20Ω resistor.
Net resistance in the circuit = 10 x 20/ 30 = 20/3 ohm
Total current in the circuit = 200/(20/3) = 30 A
So the current through 20 ohm resistor = (20/3)/20 x 30 = 10 A
Q. For the network with n resistances shown below, R1 = R2 = R3 = ………= Rn = R. Find the current passing through Rn.
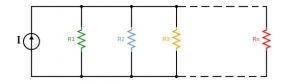
Equivalent resistance of the circuit,

We know the total current in the circuit is I
Therefore, current through Rn = (R/n)/R x I = I/n
Frequently Asked Questions | Short Notes | FAQs
Q. How can we calculate the current division?
Current division occurs in a parallel circuit. The supply current gets divided into branches connected in parallel. The voltage across all the branch resistors is equal to voltage supplied. With the help of Ohm’s law and Kirchhoff’s current law, the current division is calculated. The divided current in one branch is the multiplication of the total current and the ratio of the other branch’s resistance with the sum of all the resistance.
Q. In which condition is the current divider rule applicable?
The currentdivider rule is applicable for any circuit where resistance or other impedance parameters are connected in parallel.
Q. What is the advantage of applying the current-divider rule in a parallel circuitry ?
The basic reason for using the current-divider rule in parallel circuits is to make problem-solving easier. In a parallel circuit, the current gets divided into branches, So calculating current thru the branches becomes less time-consuming if the total current is known.
Q. Does the current division rule disobey Ohm’s law?
The Current-divider rule is based on Ohm’s law itself. The fundamental concept of Ohm’s law is used to calculate the divided currents.
Q. State the difference between a voltage divider and a current divider?
The main difference between a voltage divider and a current-divider is the operating circuit. The Voltage divider rule is applied in series circuits where as the current-divider rule is utilized in parallel circuit.
Q. When can we apply the voltage divider and the current divider rule?
In a series circuit, the voltage divider rule is used to calculate the voltage drop across the resistors. In a parallel circuit, the current-divider rule is used to calculate the branch currents.
Q. What are the voltage dividers?
The voltage dividers are linear circuits where the output voltage is obtained from the fraction of input voltage. The most common example of voltage is a potentiometer.
Q. How to use a rheostat so that it works as a potential divider and current limiter?
A rheostat can be used as a large variable resistor. It has three terminals, two at the ends and one movable contact. By adding voltage sources at the ending terminals, the voltage across the other terminal is obtained. This way the rheostat works as a potential divider, and the terminals work as current limiters.
Q. What are the advantages of a voltage divider?
A voltage divider helps in getting the voltage drop across components from the large supply voltage.
Q. How can we calculate the value of current passing through the resistor R1 in the circuit?
The current through resistor R1 is the total current multiplied by the other resistance divided by the sum of all resistance in the circuit.
Q.Why cannot we use the voltage divider method to get a constant current?
The supply voltage keeps fluctuating in a circuit. So we cannot get a constant current.
Q. Three parallel branches with resistances are connected across a DC voltage. What would be the ratio of the branch currents I1, I2, and I3 if the branch resistance ratio is R1: R2 : R3 = 2 : 4 : 6?
Let us assume that R1 = 2x ohm, R2 = 4x ohm and R3 = 6x ohm
Equivalent resistance of the circuit = 2x x 4x x 6x/ 8×2 + 24×2 + 12×2 = 12x/11 ohm
Therefore, I1 = I x 12x/11/(2x) = 6I/11 A
I2 = I x 12x/11/(4x) = 3I/11 A
I3 = I x 12x/11/(6x) = 2I/11 A
So I1 : I2 : I3 = 6:3:2
Q. Can we apply the voltage divider rule in an ac circuit?
Voltage divider rule is equally applicable for AC circuit calculations, but only if phasor representation is used involving the imaginary quantity ‘j’.
Q. How to obtain zero output voltage using a potential divider?
Zero output voltage can be achieved by keeping a potentiometer in series with a resistance. When this combination is subjected to supply voltage, an end terminal and the middle terminal of the potentiometer fetch output. When the slider terminal is at one end, the voltage is zero.
Q. In a series RC circuitry, the voltage across the capacitor and resistor are 60V & 80V, then What will be total voltage in the circuitry?
By simply applying voltage divider rule, the total voltage is the summation of the voltages across the resistors and the capacitors, So Total voltage = VR+VC=60+80=140V.
Q. Current flow is divided between the different branches in a __.
The answer would be parallel circuitry.
Q. Does a voltage divider affect current?
A voltage divider is nothing but a parallel circuit,will not affect the total current of the circuit. However, the branch current values differ according to the branch impedance.
Q. Is current divided in a parallel circuit?
By the rule of current division, we can say that the parallel circuits divide current flowing through them.