Sudipta Roy

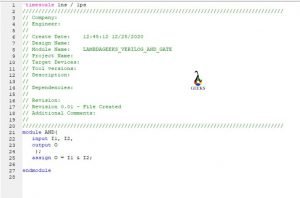
Points of Discussions

• Introduction to AC Circuit
• Important terminologies related to AC Circuit
• Pure Resistive AC Circuit
  • Phasor Diagram of a purely resistive circuit
  • Power in a purely resistive circuit
• Pure Capacitive AC Circuit
  • Phasor Diagram of Pure capacitive circuit
  • Power in a purely capacitive circuit
• Pure Inductive AC Circuit
  • Phasor Diagram of Pure inductive circuit
  • Power in a purely inductive circuit

Introduction to AC Circuit

AC stands for alternating current. If the flow of charge from an energy source changes periodically, the circuit will be referred to as an AC circuit. The voltage and current (both magnitude and direction) of an AC circuit changes with time.

AC circuit comes up with additional resistance towards current flow as impedance and reactance are also present in AC circuits. In this article, we will discuss three elementary yet important and fundamental AC circuits. We will find out the voltage and current equations, phasor diagrams, power formats for them. More complicated yet basic circuits can be derived from these circuit, like – Series RC Circuits, Series LC circuits, Series RLC circuits, etc.

What is DC Circuit? Learn About KCL , KVL! Click Here!

Important terminologies related to AC Circuit

Analysing the AC circuit and studying them needs some basic knowledge of electrical engineering. Some of the frequently used terminologies are noted down below for references. Study them briefly before exploring the AC circuit family.

• Amplitude: Power flows in the AC circuit in the form of sinusoidal waves. Amplitude refers to the maximum magnitude of the wave that can be reached in both the positive and negative domains. The maximum magnitude is represented as Vm and Im (for voltage and current, respectively).
• Alternation: Sinusoidal signals have a period of 360^o. That means the wave repeats itself after a 360^o time span. Half of this cycle is referred to as alternation.
• Instantaneous value: Magnitude of voltage and current given at any instant of time is known as instantaneous value.
• Frequency: Frequency is given by the number of cycles created by a wave in once second time span. The unit of frequency is given by Hertz (Hz).
• Time period: Time period can be defined as the time span taken by a wave to complete one full cycle.
• Wave form: Wave form is the graphical representation of the propagation of waves.
• RMS values: RMS value means the ‘root mean square’ value. RMS value of any AC components represents the DC equivalent value of the quantity.

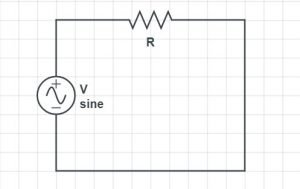
Pure Resistive AC Circuit

If an AC circuit only consists of a pure resistance, then that circuit will be called as Pure Resistive AC Circuit. There is no inductor or capacitor involved in this type of AC circuit. In this circuit, the power generated by the resistance and the energy components, voltage and currents, stay in an identical phase. That ensures the rise of voltage and current for the peak value or the maximum value occurs at the same time.

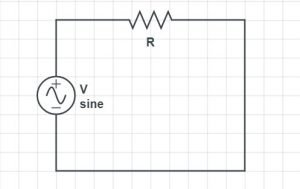
Let us assume the source voltage is V, the resistance value is R, the current flowing through the circuit is I. Resistance is connected in series. The below equation gives the voltage of the circuit.

V = V_m Sinωt

Now, from Ohm’s law, we know that V= IR, or I = V / R

So, the current I will be,

I = (V_m / R) Sinωt

Or, I = I_m Sinωt; I_m = V_m / R

The current and voltage will have the maximum value for ωt = 90^o.

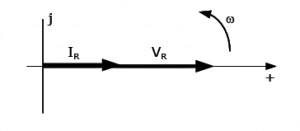
Phasor Diagram of a purely resistive circuit

Observing the equations, we can conclude that there is no phase difference between the circuit’s current and voltage. That means the phase angle difference between the two energy components will be zero. So, there is no lag or lead in between voltage and current of the pure resistive AC circuit.

Power in a purely resistive circuit

As mentioned earlier, current and voltage remain in the same phase in the circuit. The power is given as a multiplication of voltage and current. Proposed for AC circuits, the instantaneous values of voltage and current is taken into considerations intended for the calculation of power.

So, power can be written as – P = V_m Sinωt * I_m Sinωt.

Or, P = (V_m * I_m /2) * 2 Sinω²t

Or, P = (V_m /√2) * (I_m/ √2) * (1 – Cos2ωt)

Or, P = (V_m /√2) * (I_m/ √2) – (V_m /√2) * (I_m/ √2) * Cos2ωt

Now for average power in ac circuit,

P = Average of [(V_m /√2) * (I_m/ √2)] – Average of [ (V_m /√2) * (I_m/ √2) * Cos2ωt]

Now, Cos2ωt comes as zero.

So, the power comes as – P = V_r.m.s *I_r.m.s.

Here, P stands for average power, V_r.m.s stands for root mean square voltage, and I_r.m.s stands for root mean square value of current.

Pure Capacitive AC Circuit

 If an AC circuit only consists of a pure capacitor, then that circuit will be called as pure capacitive AC circuit. There is not any resistor or inductor involved in this form of AC circuit. A typical capacitor is a passive electrical device that stores electrical energy in an electric field. It is a two-terminal device. Capacitance is known as the effect of the capacitor. Capacitance has a unit – Farad(F).

When voltage is applied across the capacitor, the capacitor gets charged, and after some time, it starts discharging when the voltage source is taken away.

Let us assume that the source voltage is V; the capacitor has a capacitance of C, the current flowing through the circuit is I.

The below equation gives the voltage of the circuit.

V = V_m Sinωt

The capacitor’s charge is given by Q =CV, and I = dQ / dt gives the current inside the circuit.

So, I = C dV/dt; as I = dQ/dt.

Or, I = C d (V_m Sinωt)/dt

Or, I = V_m C d (Sinωt) / dt

Or, I = ω V_m C Cosωt.

Or, I = [V_m /(1/ωC)] sin (ωt + π/2)

Or, I = (V_m / Xc) * sin (ωt + π/2)

Xc is known as the reactance of the AC circuit (specifically the capacitive reactance). The maximum current will be observed when (ωt + π/2) = 90^o.

So, the Im = Vm / Xc

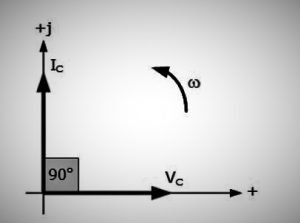
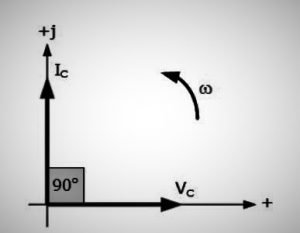
Phasor Diagram of Pure capacitive circuit

Observing the equations, we can conclude that the circuit’s voltage leads over the current value by an angle of 90 degrees. The phasor diagram of the circuit is given below.

Power in a purely capacitive circuit

As mentioned earlier, the voltage phase has a lead over current by 90 degrees in the circuit. The power is given as a multiplication of voltage and current. For AC circuits calculations, the instantaneous values of voltage and current are taken into consideration intended for the calculation of power.

So, power for this circuit can be written as – P = V_m Sinωt * I_m Sin (ωt + π/2)

Or, P = (V_m * I_m * Sinωt * Cosωt)

Or, P = (V_m /√2) * (I_m/ √2) * Sin2ωt

Or, P = 0

So from the derivations, we can say that the average power of the capacitive circuit is zero.

Pure Inductive AC Circuit

 If an AC circuit only consists of a pure inductor, then that circuit will be called as pure inductive AC circuit. There is not at all resistors or capacitors are involved in this type of AC circuit. A typical inductor is a passive electrical device that stores electrical energy in the magnetic fields. It is a two-terminal device. Inductance is known as the effect of the inductor. Inductance has a unit – Henry(H). The stored energy might also be returned to the circuit as current.

Let us assume that the source voltage is V; the inductor has an inductance of L, the current flowing through the circuit is I.

The below equation gives the voltage of the circuit.

V = V_m Sinωt

The induced voltage is given by – E = – L dI/dt

So, V = – E

Or, V = – (- L dI/dt)

Or, V_m Sinωt = L dI/dt

Or, dI = (Vm/L) Sinωt dt

Now, applying integration on both sides, we can write.

Or, ∫ dI = ∫ (Vm/L) Sinωt dt

Or, I = (Vm/ ωL) * (- Cosωt)

Or, I = (Vm/ ωL) sin (ωt – π/2)

Or, I = (Vm/ XL) sin (ωt – π/2)

Here, X_L = ωL and is known as inductive reactance of the circuit.

The maximum current will be observed when (ωt – π/2) = 90^o.

So, the Im = Vm / X_L

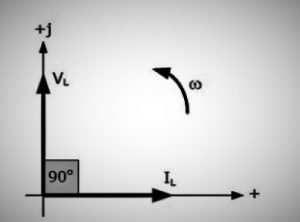
Phasor Diagram of Pure inductive circuit

Observing the equations, we can conclude that the circuit current leads over the voltage value by an angle of 90 degrees. The phasor diagram of the circuit is given below.

Power in a purely inductive circuit

As mentioned earlier, a current phase has a lead over voltage by 90 degrees in the circuit. The power is given as a multiplication of voltage and current. For Ac circuits, the instantaneous values of voltage and current is taken into considerations utilized for the calculation of power.

So, power for this circuit can be written as – P = V_m Sinωt * I_m Sin (ωt – π/2)

Or, P = (V_m * I_m * Sinωt * Cosωt)

Or, P = (V_m /√2) * (I_m/ √2) * Sin2ωt

Or, P = 0

So, from the derivations, we can say that the inductive circuit’s average power is zero.

Points of Discussion : DC Circuits

1. Introduction to DC Circuits
2. Kirchhoff’s Laws
3. Kirchhoff’s Current Law (KCL)
4. Kirchhoff’s Voltage Law (KVL)
5. Node Voltage Method
6. Mesh Current Method
7. Loop Current Method
8. Some Important Questions related to DC Circuits

Introduction to DC Circuits

DC stands for Direct Current. If the energy source phase doesn’t change with time, then the circuit will be referred to as DC Circuits. Primary energy sources for DC Circuits are batteries or similar steady power suppliers. They have a range from 5 Volts to 24 Volts. Seeing the energy symbol of a circuit, one can understand whether it is AC Circuit or DC Circuits. The symbols are given below.

Kirchhoff’s Laws

Gustav Robert Kirchhoff was an eminent physicist of German origin. His research related to electrical circuits gave us two primaries yet the most critical laws for circuit analysis. These laws are typically known as Kirchhoff’s laws. He had come up with laws for both current and voltage. They are popularly known as – Kirchhoff’s Current law and Kirchhoff’s Voltage Law. These laws are fundamental rules for DC circuits analysis.

Before studying Kirchhoff’s laws, one should have basic circuit properties of nodes, junctions, loops, mesh, branches, etc. Some definitions are given below; please check the circuit analysis article for more such primary terminologies.

• Node / Junctions: Node or junction in a circuit is known as the connecting point of two or more numbers of components.
• Loop: A loop in a circuit is defined as a closed path starting from a specific node, traveling through any part of the circuit, and ends at that specific point. There is a point to be remembered that the path can travel any circuit part only for once.  A loop can include or overlap with any other loop of the circuit.
• Mesh: Mesh can be said as the smallest loop possible in a circuit that has no overlap and doesn’t include any other loop within it.
• Kirchhoff’s Current Law is often interpreted as the First Law of Kirchhoff’s or Kirchhoff’s Junction law. It deals with the current equations of a node or junction.
• Kirchhoff’s Voltage law is often interpreted as the Second Law of Kirchhoff’s or Kirchhoff’s loop law. It deals with the voltage equations of a loop.

Kirchhoff’s Current Law (KCL)

“Kirchhoff’s current law states that the summation of the incoming current to a node is equal to the summation of the outgoing current from the node.”

Mathematically it can be stated as the following equation.

∑I_in = ∑ I_out

From the above image, we can observe that the currents I₁ and I₄ are incoming to the node while I₂ and I₃ are outgoing currents. So, we can write according to Kirchhoff’s Current Law that –

I₁ + I₄ = I₂ + I₃

Or, I₁ + I₄ – I₂ – I₃ = 0

Concept Check: What will be the current value for the branch I₅? Provided that I₁= 2 mA, I₂= 1 mA, I₃= 4 mA, I₄= 1 mA and I₆= 2 mA.

Solution: To solve this type of problem of DC Circuits, first find out the desired node. Then separate the incoming and outgoing current components. Then apply Kirchhoff’s current law and find out the solution.

The incoming currents are I₁, I₃, I₄.

The outgoing currents are I₂, I₅, I₆.

The missing component is I₅, which is outgoing.

Now, from KCL, we know that –∑I_in = ∑ I_out

So, we can write –

I₁ + I₃ + I₄ = I₂ + I₅ + I₆

Or, I₅ = I₁ + I₃ + I₄ – I₂ – I₆

Or, I₅ = 2 mA + 4 mA + 1 mA – 1 mA – 2 mA

Or, I₅ = 4 mA

Kirchhoff’s Voltage law (KVL)

Kirchhoff’s Voltage Law states that the voltage around a loop of the circuit equals zero, and the algebraic sum of voltage drop at each branch in that loop is equal zero also.

Mathematically it can be stated as the following equation.

∑ V_n = 0

V_n represents the voltage around n elements or branch of the loop.

From the above image, we can write that,

V_AB + V_BC + V_CD + V_DA = 0

Kirchhoff’s voltage law has few characteristics. Some of them are –

• While analyzing a circuit, if you start your path with a node, do not include any other loop in your path, and end your path in the same node, then the sum of voltage through that path will be zero.
• The path can be in any direction; the Clockwise or anti-clockwise path does not affect Kirchhoff’s voltage law.
• A typical complex circuit may have many loops. KVL is valid for each and every possible loop of the circuit.

Node Voltage method

The node voltage method is another useful method for the analysis of the DC circuit. It is derived from Kirchhoff’s current law. SPICE – a simulator software contains this method. Actually, this method is more comfortable to implement and analyze the whole circuit. Using the method helps us to get rid out of Kirchhoff’s voltage law if we want to.

• Node Voltage: Node voltage is a concept needed for the Node Voltage Method. This can be defined as the potential difference between two nodes.

Steps to follow: The node Voltage method can be applied to the DC circuits by following the below-mentioned steps.

• Select a reference node. In most cases, the ground node is elected.
• Name all the other nodes of the circuit.
• Start with the nodes, which seems to be easy. The energy source (preferably voltage source) node connected with the reference node would be more comfortable.
• Now apply Kirchhoff’s current law for every node. Also, do the calculations of hm’s law.
• Find out the solutions for all of the node voltages.
• Find out any current of the circuit with the help of Ohm’s law.

Mesh Current Method

The mesh current method is another efficient method for DC circuit analysis. It is derived from Kirchhoff’s Voltage Law, and a new method named “Loop current method” is derived from this method. It has an added advantage over other circuit analysis methods as it does not require to solve a 2E number of circuit equations (E stands for the number of elements of the circuit). Studying this method needs an adequate level of understandings of the concept of loops and meshes.

• Loop current: Loop current is a concept needed for this method. It is defined as the current through any loop or mesh of the circuit.
• Superposition principle: Superposition stands for general addition. Here superposition principle states that loop currents can be added together to get the actual current element.
• Linearity: Linearity characteristics help to use the principle of superposition. Linearity is multiplying voltage with a constant and getting the current as constant the multiplied product.

Steps to follow: Mesh current method can be applied by following the below-mentioned steps.

• Mark the meshes (known as open windows of the circuit).
• Choose a specific constant current direction (either clockwise or anti-clockwise), which all be applied for every mesh. Also, give current variables to each mesh.
• Apply Kirchhoff’s Voltage law for each mesh and write down the equations.
• Calculate the resulting system for all the mesh equations.
• Using Ohm’s law, find out the desired current and voltage components.

Loop current Method

We can say that the Loop current method is an updated version of the Mesh Current method. This method is popular and helpful for non-planar circuits.

Steps to follow: loop current method can be used to analyse DC circuits using the below-mentioned steps.

• Mark the meshes (known as an open window of the circuit). Also, identify the loops.
• Choose a specific constant current direction (either clockwise or anti-clockwise), which all be applied for every mesh. Also, give current variables to each mesh or the loops.
• Calculate the resulting system for all the mesh and loop current equations.
• Using Ohm’s law, find out the desired voltage and current component.  

Some important questions related to DC Circuits

1. What is the main idea behind Kirchhoff’s current law?

Answer: The main idea behind Kirchhoff’s current law is the theory that charges cannot be accumulated at one point.

2. Write some limitations of Kirchhoff’s laws.

Answer: Kirchhoff’s both laws have some limitations. They are listed below.

• Kirchhoff’s current law comes with the assumption that conductors and wires are the only media for the flow of current. In reality, in high-frequency circuits, we can observe the flow of current in open circuits as standard conductors work as transmission lines.

• Kirchhoff’s Voltage law comes up with the assumption that every closed loop of the circuit will be free from the effect of the magnetic field, more specifically, the fluctuating magnetic field. But, in the high-frequency circuits, this condition doesn’t get satisfied.

3. Nodal analysis is based on the law of energy conservation—state whether the given sentence is true or false.

Answer: False. Nodal analysis is based on Kirchhoff’s current law, and also Kirchhoff’s first law supports the conservation of charges, not energy.

4. What is the effect on the circuit’s current if the energy sources are connected in parallel?

Answer: The current of the whole circuit gets increased.

Bildnachweis – “Freundschaft an Bord”(CC DURCH-NC-ND 2.0) durch Elf-8

Diskussionspunkte

• Einführung in die Parabolreflektorantenne
• Übersicht der Parabolreflektorantenne
• Anwendungen der Parabolreflektorantenne
• Eigenschaften
• Geometrieanalyse
• Richtwirkung der Parabolreflektorantenne
• Apertureffizienz der Parabolreflektorantenne
• Mathematische Probleme

Einführung in die Parabolreflektorantenne

Antenne oder Strahler ist ein Mittel zum Strahlen und Empfangen elektromagnetischer Informationen. Parabolreflektorantenne ist eine der weit verbreiteten Antennen. Es ist ein besonderer Typ von Reflektorantennen. Der Einsatz von Reflektorantennen begann mit dem Beginn des Zweiten Weltkriegs mit der Weiterentwicklung der Kommunikationstechnologien.

The most straight-forward reflector and more comfortable to implement the reflector antenna is ‘Plane Reflector’ antenna. There are some other types of reflectors also, like – corner reflector, parabolic reflector, Cassegrain reflectors, spherical reflectors. Parabolic reflectors have another type known as ‘Front fed parabolic reflector antenna’.

Was ist eine Hornantenne? Erkunden hier!

Übersicht der Parabolreflektorantenne

Die Strahlungsparameter einer Reflektorantenne können durch Verbesserung des Strukturmusters des Bodens verbessert werden. Auf diesem Gebiet kommt für diesen Parabolreflektor die optische Wissenschaft ins Spiel. Die optische Mathematik beweist, dass einfallende parallele Strahlen durch Reflexion an einer parabelförmigen Struktur zu einem bestimmten Punkt (bekannt als Brennpunkt) konvergiert werden können.

Die reflektierten Wellenformen treten als paralleler Strahl aus. Dies ist ein mathematisches Phänomen, das als “Reziprozitätsregel” bekannt ist. Der proportionierte Punkt wird als Scheitelpunkt bezeichnet. Die ausgehenden, reflektierten Strahlen werden als kollimiert bezeichnet (da sie parallel sind). Obwohl die praktischen Beobachtungen gezeigt haben, dass die austretenden Strahlen nicht als paralleler Strahl bezeichnet werden können, unterscheiden sie sich geringfügig von der richtigen Form.

Der Sender dieser Antenne befindet sich im Allgemeinen an den Brennpunkten der Schale oder des Reflektors. Diese Art der Einrichtung wird als “Front-Feed” bezeichnet. Wir werden im nächsten Teil dieses Artikels eine Analyse dieser Art von Parabolreflektoren diskutieren.

Was macht eine Übertragungsleitung? Erforschen!

Anwendungen der Parabolreflektorantenne

Parabolreflektoren sind eine der weit verbreiteten, hocheffizienten Antennen, deren Nachfrage von Tag zu Tag steigt. Vom Empfang des Signals für unser Fernsehgerät bis zur Übertragung des Signals für die Raumstationen findet dieser Antennentyp Anwendungen in nahezu allen Bereichen der Kommunikationstechnologie. Einige der bemerkenswerten sind – auf Flughäfen, in Satelliten, in Raumstationen, in Teleskopen usw.

Eigenschaften

Einige signifikante Eigenschaften des Parabolreflektors sind unten angegeben. Die Eigenschaften betreffen Aperturamplitude, Polarisationseigenschaften, Phasenwinkel usw.

• Der Magnitudenanteil hängt vom Abstand der Einspeisung zur Reflektoroberfläche ab. Die Proportionalität variiert von Struktur zu Struktur. Wie bei einer parabelförmigen Form ist sie umgekehrt proportional zum Quadrat des Radius der Parabel, und bei einer zylindrischen Struktur ist die Beziehung umgekehrt proportional zu ρ.
• Der Brennpunkt des Reflektors wirkt für verschiedene Arten von geometrischen Konfigurationen unterschiedlich. Die zylindrische Struktur hat eine Linienquelle und parabolische Strukturen haben eine Punktquelle.
• Wenn der Vorschub lineare Polarisationen parallel zur Zylinderachse aufweist, besteht keine Möglichkeit von Kreuzpolarisationen. Parabolische Strukturen haben nicht die gleiche Eigenschaft.

Überprüfen Sie das Strahlungsmuster von Yagi Uda Antenne!

Geometrische Analyse

     Wenn eine geometrisch perfekte Parabel um ihre Achse gedreht wird, entsteht eine andere Struktur. Diese Struktur ist als Parabolreflektor bekannt. So entsteht ein parabolisch geformter Reflektor. Es gibt einen bestimmten Grund für die Form dieses Reflektors. Die parabolische Form hilft, aus den austretenden Strahlen eine einfache und ebene Wellenform zu erzeugen.

     Aus dem Bild können wir ersehen, dass die geometrische Länge OP + PQ einen konstanten Wert für das Entwerfen ergibt.

Wir können schreiben, OP + PQ = 2f; 2f ist der konstante Term.

Nehmen wir das an OP = r und so kommt PQ als PQ = r * cosϴ.

Nun ist der Wert von OP + PQ nach dem Ersetzen der Werte,

OP + PQ = r + r * cosϴ = 2f

Oder r (1 + cosϴ) = 2f

Oder r = 2f / (1 + cosϴ) = f * sec²(ϴ / 2)

In der Antennentheorie müssen wir nun die Grundlagen des Koordinatensystems in Form von Sachleistungen halten. Die obige Gleichung kann in rechteckigen Koordinatensystemen unter Verwendung von x`, y`, z` geschrieben werden. Das ergibt die folgende Form.

r + r * cosϴ = √ [(x`) 2 + (y`) 2 + (z`) 2] + z` = 2f

Lassen Sie uns den Einheitsvektor herausfinden, der senkrecht zur Tangente des Reflexionspunktes ist.

f – r * cos²(ϴ / 2) = 0 = S.

Durch einige Rechenoperationen finden wir den Einheitsvektor. Es wird unten beschrieben.

n = N / | N | = – (a) `<sub>r</sub> cos (ϴ / 2) + – (a) `_ϴ Sünde (ϴ / 2)

Mithilfe der geometrischen Analyse können wir nun einen Ausdruck für den Neigungswinkel finden. Es wird unten beschrieben.

tan (ϴ₀) = (d / 2) Z.₀

Das Z₀ ist die Messung der Entfernung von der Achse zum Brennpunkt. Mathematische Ausdrücke können es auch darstellen.

Z₀ = f – [(x₀² + y₀²) / 4f]

Oder Z.₀ = f – [(d / 2)²/ 4f]

Oder Z.₀= f – d² / 16f

Überprüfen wir den Wert von tan (ϴ₀) nach dem Ersetzen des Wertes von Z0.

tan (ϴ₀) = [(f / 2d) / {(f / d)² – (1/16)}]

Entdecken Sie die Anwendungen der Helixantenne! Klick hier!

Richtwirkung der Parabolreflektorantenne

Bevor wir uns mit der Richtwirkung einer Parabolantenne befassen, informieren Sie uns über die Richtwirkung einer Antenne.

Die Richtwirkung einer Antenne ist definiert als das Verhältnis der Strahlungsintensität einer Antenne in einer bestimmten Richtung zur gemittelten Strahlungsintensität über alle Richtungen.

Die Richtwirkung wird als Parameter zur Berechnung der Gütezahl der Antenne betrachtet. Der folgende mathematische Ausdruck beschreibt die Richtwirkung.

D = U / U.₀ = 4πU / P._rad

Wenn die Richtung nicht angegeben ist, ist die Standardrichtung die Richtung der maximalen Strahlungsintensität.

D_max = D₀ = U._max / U.₀ = 4πU_max / P_rad

Hier ist ‘D’ die Richtwirkung und hat keine Richtung, da es sich um ein Verhältnis handelt. U ist die Strahlungsintensität. U._max ist die maximale Strahlungsintensität. U.₀ ist die Strahlungsintensität der isotropen Quelle. P._rad ist die gesamte abgestrahlte Leistung. Seine Einheit ist Watt (W).

U = ½ r² * | E (r, ϴ = π) |² * √ (ε / μ)

Für U (ϴ = π) und Ersetzen des Energiewerts E wird aus dem vorherigen Wert –

U (ϴ = π) = [16 π² f² * Pt * | ∫.₀ ^ϴ tan (ϴ / 2) * √ (G._f (ϴ)) dϴ |²] / 4πλ²

Die Direktivität kommt als – D = U / U.₀ = 4πU / P._rad

Oder D = [16 π² f² * | ∫.₀ ^ϴ tan (ϴ / 2) * √ (G._f (ϴ)) dϴ |²] /²

Apertureffizienz der Parabolreflektorantenne

          Der mathematische Ausdruck für die Parabolreflektorantenne ist unten angegeben.

          ε_ap =_s * ε_t * ε_p * ε_x * ε_b * ε_r

Hier

ε_ap repräsentiert die Apertureffizienz.

ε_s ist Spillover-Effizienz. Es kann als der Teil der Leistung definiert werden, der von der Einspeisung übertragen und von der Oberfläche der Reflexion parallel geschaltet wird.

ε_t repräsentiert die Effizienz der Verjüngung. Es kann als die Singularität der Streuung der Größe für das Feed-Design über die Oberfläche des Reflektors beschrieben werden.

ε_p gibt uns die Effizienz der Phase. Es kann als die Gleichmäßigkeit der praktischen Feldphase über die Ebene der Apertur beschrieben werden.

ε_x repräsentiert die Effizienz der Polarisation.

ε_b ist die Effizienz des Rückstands.

Und ε_r stellt die Fehlereffizienz dar, berechnet über die gesamte Reflektorfläche.

Mathematisches Problem

1. Eine Parabolreflektorantenne hat einen Durchmesser von 10 Metern. Das f / d-Verhältnis wird mit 0.5 angegeben. Die Betriebsfrequenz ist auf 3 GHz eingestellt. Die Antenne, die mit dem Reflektor gespeist wird, ist symmetrisch aufgebaut. Es ist auch gegeben, dass –

G_f (ϴ) = 6 cos²ϴ; wo ϴ^o ≤ ϴ ≤ 90^o und null an jedem anderen Punkt.

Berechnen Sie nun i) die Apertureffizienz (ε_ap). ii) Richtwirkung der Antenne. iii) Verjüngungseffizienz und Effizienz des Überlaufens. iv) Ermitteln Sie die Richtwirkung der Antenne, wenn die Aperturphasenabweichung auf π / 4 Radian eingestellt ist.

Lösung:

          Wir wissen, dass der Neigungswinkel durch den folgenden Ausdruck gegeben ist.

tan (ϴ₀) = [(f / 2d) / {(f / d)² – (1/16)}]

Oder tan (ϴ₀) = [(0.5 · 0.5) / {(0.5 · 0.5) – (1/16)}]

Oder tan (ϴ₀) = 0.25 / 0.0625

Oder ϴ₀ = 53.13^o

Die Apertureffizienz ist gegeben als –

ε_ap = 24 [(Sünde² (26.57^o) + ln {cos (26.57^o)}]² * Kinderbett²(26.57^o)

oder ε_ap = 0.75

Der Öffnungswirkungsgrad beträgt also 75%.

Lassen Sie uns nun die Richtwirkung der Antenne herausfinden.

Es kann wie folgt berechnet werden.

D = 0.75 * [π * (100)]²

Oder D = 74022.03

Oder D = 48.69 dB.

Die Überlauffrequenz beträgt ε_s.

ε_s = 2 cos³ |₀ ^53.13 / 2 cos³ |₀ ⁹⁰ 

oder ε_s = 0.784

Die Spillover-Effizienz der Antenne beträgt also 78.4%.

Jetzt Zeit für die Berechnung der Effizienz des Gewindeschneiders. Die Tapper-Effizienz wird als & epsi; dargestellt_t.

ε_t = (2 · 0.75) / 1.568

oder ε_t = 0.9566

Der Tapper-Wirkungsgrad für die Parabolreflektorantenne beträgt also 95.66%.

Jetzt wird die Aperturphasenabweichung auf π / 4 Radian eingestellt.

Das heißt m = π / 4 = 0.7854

Wir wissen, dass D / D.₀ ≥ [1 – m²/ 2]²

Oder D / D.₀ ≥ [1 – (0.7854 * 0.7854) / 2]²

Oder D / D.₀ ≥ 0.4782737

Oder D ≥ 0.4782737 * D._0.

Oder D = 0.4782737 * 74022.03

Oder D = 35402.8

Oder D = 45.5 dB.

Die Richtwirkung unter den gegebenen Bedingungen beträgt 45.5 dB.

Cover Image Credit – Service Depicted: Air Force
Camera Operator: SSGT LOUIS COMEGER, Hammer Ace SATCOM Antenna, marked as public domain, more details on Wikimedia Commons

Points of Discussions

• Introduction
• Geometrical Analysis and Configurations
• Operational Modes
• Normal Mode
• Axial Mode
• Helical antenna design
• Helical antenna applications

Introduction to Helical Antenna

            To define a helical antenna, we must know the correct definition of the antenna previously. As per to IEEE standard definitions of antennas or radiators,

“An antenna is a medium for transmitting and receiving radio waves”.

There are several adaptations of antennas. Some of them are – dipole antennas, horn antennas, log-periodic antennas, patch antennas, broadband antennas etc.

          The helical antennas or helix antennas are one of the categories of broadband antennas. It is one of the most straightforward, primary and realistic antennas with a helical structure, made up of conducting wire-wound.

What is a horn antenna? Explore here!

Geometrical analysis and configuration

          Helical antennas or helix antennas generally come with a ground plane which has the ability to accept distinct forms. To establish a typical helix connection with the ground plane, the ground plane’s diameter should be minimum of 3*λ/4. Although, the plane may be transfused into a cylindrical shaped crater. At the feed point, the transmission lines meet with the antenna.

          The geometrical description of a helix antenna typically consists of N number of turns, the diameter D and the distance between two helical loop S.

The whole length is given by –> L = N S.

The conductive wire’s whole length is given by –> L_n = N L₀ (It carries the current primarily obviously!)

 Or, L_n = N √ (C² + S²); L₀ = √ (C² + S²)

L₀ represents the dimension of the wire between two helical loops. It actually gives the length.

C represents the whole circumference of a spiral loop, and it is given by -> π D.

There is another spiral or helix antenna’s parameter, which is also very important. It is represented by the Greek alphabet alpha(α) and termed as ‘pitch angle’. This angle is generally the measurement of the line’s angle – normal to the helix wire and a steep ground to the helix axis. The mathematical expression is given below.

α = tan^-1 (S/C)

or, α = tan^-1 (S/ π D)

By carefully observing the equation, it can be concluded that when the angle tends to 0 degrees, the winding gets trampled; as a result, the helix antenna gets reduced and becomes similar to a simple loop antenna. Again, when the angle becomes 90 degrees, the antenna becomes a linear wire. When the angle is less than 90 degrees and greater than 0 degrees, then a practical helix has a finite value of circumference.

The architectural parameters can change the radiation properties of the helix antennas. Controlling the geometrical parameters will vary the radiation properties associated with the wavelength. The input impedance has a relation with the pitch angle and conducting wire’s size, as a change in pitch angle values, and the size of the wire will change the input impedance values.

Helical antenna typically shows elliptical polarization, although they can be designed to show circular and linear polarization.

Operational Modes

Helix antennas have the capability to function in many types of operational modes. There are two significant and essential operational modes that we will discuss in detail in the latter part of this article. The two modes are –

• Axial Modes (End- Fire)
• Normal (Broadside)

The three-dimensional figures of both the types of mode of operations are given below.

As we can see in the standard figure, it has a maximum in an imaginary plane which is normal to the axis, and its null is along the axis. The power pattern has a close similarity to the shape of the circular loop.

Now, the maximum is along the helix’s length for the end-fire mode, and the power pattern is similar to the end-fire array. That is why the mode is named as ‘End Fire Mode’.

The axial mode of operation has more preference over the standard mode of operation because it is more realistic or practical, has better efficiency and can show circular polarization with a broader bandwidth. An elliptically polarized antenna can be described as the summation of the two extraneous lined mechanisms in phase-time quadrature.

What does a transmission line do? Explore!

Normal Mode of Helix Antennas

As discussed previously, the antenna’s helical mode has its maximum radiation is directed to a plane normal to the helix axis, and the null radiation is along its axis. The normal mode of operation of helix antenna or broadside mode operation is achievable by comparing the wavelength, that is N L₀ << λ_0.

The helix architecture comes down to a loop of a diameter D as the pitch angle comes to 0 to a lined wire with a length of S while approaching to 90 degrees. Nos, as the helix’s geometry, became a loop and a dipole, the far-field radiation in this mode of operation can be represented respectively by E_ϕ and E_ϴ components of the dipole and the spiral loop.

The helix can be described as N number of small loops and the same number of small dipoles. They are linked with each other in a series manner. The arenas are calculated by using the superposition of the other fields from the rudimentary parts. The loop’s axes and the dipole’s axes coincide with the helix’s axis.

As this model has small dimensions, the current is assumed to be constant. Its operation can be defined by the summation of the fields radiated by a smaller-loops, having a diameter of D and a short dipole having a length of S.

The far-field electric field is given as –

E_ϴ = j * η * k * I₀ * S * e^-jkr Sinϴ / 4πr

The E_ϕ part is given by –

E_ϕ = η* k² * (D/2)² * I₀ * e^-jkr Sinϴ /4r

The ratio of Eϴ and Eϕ gives the axial ratio. The mathematical expression is given below.

AR = | E_ϴ | / | E_ϕ |

Or, AR = 4S / πkD²

Or, AR = 2λS/ (πD)²

The pitch angle is given as – α = tan^-1 (π D/2λ₀)

Axial Mode of operation for Helical Antenna

The axial mode of operation has more preference over the standard mode of operation because it is more realistic or practical, has better efficiency and can show circular polarization with a broader bandwidth.

          This mode is achieved by setting up large S and D. There are some requirements for achieving circular polarization. The range of the circumference of the helix should be in the below-given range.

4/3 > λ₀/C > ¾

The pitch angle also has a limited range. The range of the pitch angle is given below.

12^o ≤ α ≤ 14^o

The terminal impedance range for this mode of operation is between one hundred ohms to two hundred ohms.

The following mathematical operation calculates the gain. For the following equation, S gives the distance between two turns, and N represents the total number of turns in a helical antenna.

G = 15 (C / λ) ² * (NS / λ)

The half-power bandwidth of helical antenna for this mode of operation is given by following mathematical expression.

HPBW = 52 / [ (C/ λ) * √ {(NS / λ)}]

The full null bandwidth of helical antenna for this mode of operation is given by following mathematical expression.

FNBW = 115 λ^3/2 / C * √ (NS)

Check out the radiation pattern of Yagi Uda Antenna!

Helical Antenna Design

• The input impedance is represented as ‘R’. The mathematical equation for ‘R’ is – R = 140 (C / λ₀).
• The half-power bandwidth of helical antenna for this mode of operation is given by following mathematical expression. It has the accuracy of around plus-minus twenty percent. It is a measurement of angle and has a unit in degrees.

HPBW = 52 λ^3/2 / C * √ (NS)

• The full null bandwidth of helical antenna for this mode of operation is given by following mathematical expression. It represents the measure of beamwidth among the Nulls. It has also unit in degrees.

FNBW = 115 λ^3/2 / C * √ (NS)

• D0 represents the directivity of the antenna. The mathematical equation is –

D₀ = 15 * N * C²S / λ₀³

• The following mathematical term gives the Axial Ratio or the AR.

AR = 2N+1 / 2N

• The following expressions give the generalized far-field pattern.

E = sin (π/ 2N) cosϴ sin [ (N/2) * Ψ] / sin (Ψ /2)

Ψ is given by another mathematical equation, and that is further given as Ψ = k₀[S * cos ϴ – (L₀/p)]

                    The value of ‘p’ for general end-fire array is

p = (L₀/ λ₀) * (S/ λ₀ + 1)

                    The value of ‘p’ for Hansen-woodyard end-fire radiation is

                                        p = (L₀/ λ₀) * [S/ λ₀ + {(2N+1)/2N)}]

Helical Antenna Applications

The helical antenna has several applications in modern communication technologies. It has some unique applications because of its design and radiation patterns. Some of the spiral antenna applications are listed below.

• Helical antennas are efficient in radiating very high-frequency range signals.

• Helical antennas are often used for space communications and satellites communications.
• Communications between two planets are possible because of these types of antennas.

Image Credit : Raysonho @ Open Grid Scheduler / Grid Engine, YagiAntenna, CC0 1.0

Points for Discussion

• Introduction
• Use of Yagi uda antenna
• Elements of a typical Yagi Uda antenna
• Yagi uda antenna construction
• Yagi Uda Antenna Design
• Yagi uda antenna radiation pattern
• Few mathematical problems related to Yagi-Uda antenna

Introduction

To define a Yagi-Uda antenna, we should know the proper definition of the antenna. According to IEEE standard definitions of antennas, “An antenna is a means for radiating or receiving radio waves”.

A yagi-uda antenna is basically an array of rectilinear dipoles with a feed element and other parasitic elements. It can be described as an end-fire array which means the array is set of internally connected antennas and the total unit functions as a single antenna.

Yagi Uda antenna is a very realistic antenna for the high-frequency domain as it operates in the high-frequency field to an ultra-high frequency domain.

Professor S. Uda and professor H. Yagi of Tohoku Imperial University, Japan, first described this type of antenna’s operation. The antenna is often interrupted as ‘Yagi Antenna’.

What is horn Antenna? Check out here!

Use of yagi uda antenna || Applications of yagi uda antenna

            Yagi antenna is one of the widely used antennae. It has been used as TV antennas at uncountable homes due to its high directivity. Many readers would recognize it just seeing the picture. It has application in amateur radios, in fields of RADARs, in satellites and RFID applications.

Elements of a typical Yagi Uda antenna

As earlier said, a typical Yagi Uda antenna, is an array of small antennas and it has one element for energy feed and others are parasitic.

The most used feed element of a yagi uda antenna is a folded dipole. The radiator is specially constructed for operation of an end-fire array. Parasitic elements at the forward beam act as directors and the pieces at the rear beam act as reflectors. This completes the antenna.

The thin rods are aligned on a crossbar with their centres. There is one driven element, several parasitic elements, a reflector, and one or more directors. As the name suggests, the parasitic elements are not physically connected with the transceiver and work as passive radiators. They radiate radio waves which further affects the radiation pattern. The distance between the two rods depends on the wavelength of the signal. Typically, the distance changes from one-tenth to one-fourth of the wavelength.

The directors’ size is generally shorter than the driven element, which is also more concise than the reflector.

The gain of a yagi uda antenna depends upon the number of parasitic elements present. Increase in the number of parasitic elements increases the overall gain of the antenna. That is why there are numerous directors in a yagi-uda antenna. As the reflector has a negligible effect on the antenna gain, there is only one reflector in the antenna.

Yagi uda antenna construction

We will discuss the construction of a few parts of the yagi uda antenna. The stakes are – Driven element, Director, & the Reflector.

• Director: It is the shortest element of the yagi uda antenna. This part is directed towards the receiving source. The length of the detectors depends upon the distance between the details and the wavelength of the signals. The gain of a yagi uda antenna has a relation with the length of the antenna. The antenna length also increases by increasing the number of directors.
• Driven element: It is the element which has the feed point for energy. The transmitter is connected with this element through the feed point. The feed point typically lies at the centre of the component. The length of the part is half of the wavelength.
• Reflectors: It is a single unit and constructed at the end of the antenna array just after the driven element. It has the highest length among the parasitic elements. The spacing of reflector depends on the wavelength, beamwidth and gain of the yagi uda antenna. The resonant frequency of reflector is generally lower.

How transmission lines are related with antennas? To know – click here!

Working of yagi uda antenna

Let us draw some attention towards the operation and working of a yagi uda antenna. Assume a typical yagi uda antenna with a reflector, with a driven element and a single director.

As discussed earlier, the driving element’s length is half of the dipole, and it is connected with electrical energy directly. It supplies power throughout the antenna as it has the feed point, and all other parasitic elements are internally associated with this element.

Now, assume the parasitic elements (both the reflectors and directors) as a general dipole element of a measurable diameter and fed at the middle via a short circuit. Transmission line theory says that a short circuit is enabled to reflect power at 180 degrees.

Thus, the operation can be designed as the mixing up of a power receiver dipole element that receives the power and sends to the matched load and a power transmitter dipole element that transmits the power to the array of the antenna.

Now, at an instant, if the received and sent power are in 180 degrees out of phase with each other, then the result will be zero voltage. That signifies the short circuit of the diode at the feed point. That is why the radiated power is in 180 degrees phase out with the incident waves.

The parasitic elements in the antenna are shorter than ½λ. The reflector is longer than ½λ, and it generally lags the phase of open-circuit voltage. The incoming signal generates the voltage. The director is also shorter than ½λ. It lags the voltage that of current.

Yagi Uda antenna design

Unlike the horn antenna, there are no hard and fast rules to design a yagi-uda antenna. There are some critical physical parameters which resist doing so. Some of the parameters are as follow –

• ‘Length of element and distance between them.’
• The measurement of the rods or the diameter of the rods.
• Some critical parameters like – Gain and input resistance.

Though, there are some methods for analysis and calculation to find out the desired results. For an n-element yagi uda antenna, there are 2n-1 numbers of parameters to consider.

The analysis for current distribution is done by solving the ‘Hallen’s integral equation’. The assumption of a classical standing wave and condition of other conductors are also taken into account. The analysis method is complicated and requires accurate results though some vital approximations are necessary to complete it.

The designed antennas go through trial-and-error methods to modify further. Sometimes, the antenna starts with a design and ends up with another after certain modifications in the process. Nowadays, computer simulation helps designers/ engineers to check the result.

Yagi Uda antenna radiation pattern

Radiation Pattern is the angular dependence of the strength of the radio waves from any electromagnetic source. The below image shows the radiation pattern of a yagi uda antenna.

Advantages yagi uda Antenna || Disadvantages of yagi uda antenna

            Yagi uda antenna has both its advantages and disadvantages. But there is no doubt that this antenna has made some drastic changes in the field of commercial antennas. It has the highest ever popularity as TV antennas because of its large bandwidth. Let us discuss some of its advantages.

Advantages of yagi uda antenna

• Yagi uda antenna has a decent gain of 7dB, which is sufficient for its applications.
• Yagi uda antenna array is direction type of antenna.
• This type of antennas is suitable for applications in high frequency to the ultra-high frequency range.
• These antennas have adjustable from to ack ratio.

Let us discuss some drawbacks of yagi uda antenna.

Disadvantages of yagi uda antenna

• Though the applications of yagi uda antennas are suitable for the antenna’s gain, the gain is not very high compared to any other types of antenna.
• The designing has a requirement of a large number of elements.
• Any damage to the parasitic elements leads to the dysfunctionality of the whole antenna.
• The size is quite large, that is why nowadays the antennas are not used by peoples.

Few mathematical problems related to Yagi Uda Antenna

1. Design a yagi uda antenna with the following specifications. Directivity: Relative to ½λ dipole and situated at the same level. Magnitude: 9.2 dB. f₀ = 50.1 MHz. The desired diameter of the parasitic rods: 2.54 cm. The desired diameter of the metal supporting boom: 5.1 cm. Find out the spacings between elements, lengths and length of the entire array.

Solution:

            The operating frequency is given as 50.1 MHz. The wavelength comes as λ = 5.988m.

The desired diameter of the parasitic rods is given as d = 2.54 cm.

Therefore, d /λ = 2.54/598.8

Or, d /λ = 4.24 x 10^-3 

The desired diameter of the metal supporting boom is given as D = 5.1cm.

Therefore, D /λ = 5.1 / 598.8

Or, D /λ = 8.52 x 10^-3

            We need to use a chart that gives us ‘optimized uncompressed lengths of parasitic elements of a yagi-uda antenna’. Using this chart, we can understand that the desired antenna array would have a total of five elements (one driven element, one reflector and three directors).

The second column of the chart gives us the optimum uncompressed length for the value of d/λ = 0.0085.

l₁ = 0.482λ

l₃ = 0.428λ

l₄ = 0.424λ

l₅ = 0.428λ

The overall antenna length will be L = (0.6 + 0.2) λ = 0.8λ. The spacing or the distance between the directors parasitic will be 0.2λ and the spacing of the reflector will be same that is 0.2λ.

Image Credit: Schwarzbeck Mess-Elektronik, Schwarzbeck BBHA 9120 D, CC BY-SA 3.0

Points for Discussion: Horn Antenna

• Introduction
• Use of horn antenna
• Elements of a horn antenna and Types of horn antenna
• Horn antenna design
• Directivity of horn antenna
• Horn antenna radiation pattern
• Horn antenna gain
• Horn antenna beamwidth
• Few mathematical problems related to Horn Antenna

Introduction

To define a horn antenna, we should know the proper definition of the antenna. According to IEEE standard definitions of antennas,

“An antenna is a means for radiating or receiving radio waves”.

Horn antenna is the most popular type of Aperture antenna. Aperture antennas are specially designed for microwave frequencies. These types of aperture antennas are widely used and most unadorned other than any kinds.

Though horn antenna usage was started back in the 1800s, the rapid application was created in the 1930s. These antennas had also undergone drastic modification during this time. Numerous thesis and research were done to describe the horn-antenna’s design, find out the radiation pattern of horn-antenna, and applications in different sectors. The applications in microwave and waveguide transmission domain made horns antenna famous. That is why horn- antennas are often interpreted as a microwave horn-antenna.

What is Transmission Line? How it is related to antenna? Know here!

Use of Horn Antenna

Horn-antennas have found impactful applications as feed elements for hefty radio astronomy, satellite tracking, communication dishes, and many other places. It is used as a feed for reflector and lenses and also used in phased arrays. These antennas are preferred over different types of aperture antennas, because of its fair and straightforward design, better gain, versatility, and overall performance.

Elements of a horn antenna

Horn antenna is a resonating pipe of various designs which can be shaped for making a larger opening. The overall performance of the antenna is affected by the direction, taper’s amount, directivity.

Types of horn antenna

Horn-antennas have different forms for operations. They are –

·       Sectoral Horn Antenna

• E-Plane
• H-Plane

·       Pyramidal Horn Antenna

·       Conical Horn Antenna

·       Corrugated horn antenna

·       Diagonal horn antenna

·       Ridged horn antenna

·       Dual-mode conical horn antenna

·       Septum horn antenna

·       Aperture-limited horn antenna

Horn antenna design (Pyramidal Horn Antenna)

Pyramidal horn-antenna is the most used and popular types of the horn-antenna. It is known as a standard gain horn (that is why we choose pyramidal horn for describing). The pyramidal horn’s radiation pattern is the combination of E- and H- sectoral horn-antennas. Let us discuss the design of a pyramidal horn-antenna.

Design Procedure

• The designer/ engineer should know the gain (G₀). Also the measurements of ‘a’, ‘b’, of the quadrilateral waveguide (used as feed) should be known.  
• The designing aims to derive dimensions such as – a₁, b₁, ρ_e, ρ_h, P_e, P_h. The calculation should lead the designer to the optimum gain of the horn- antenna.
• The selection of a1 and b1 should also be in a guided way so that they will help to find the optimum gain, and we can derive the design equations.
• The efficiency of a horn- antenna including the apertures is about 50%. Now, we know that –

a₁ ≈ √ (3λρ₂)

b₁ ≈ √ (2λρ₁)

The directivity is given as – D₀

D₀ = A_em [ 4π / λ²]

A_em is the maximum effective area and has a relationship with the physical area (abbreviated as A_p).

A_em = ε_ap A_p

ε_ap is the aperture efficiency, 0 ≤ ε_ap ≤ 1

Gain = G₀

G₀ = (1/2) * (4π / λ²) * (a₁ b₁)

Or, G₀ = (2π / λ²) * √ (3λρ₂) * √ (2λρ₁)

Or, G₀ ≈ (2π / λ²) * √ (3λρ_h * 2λρ_e) — (1)

As we assume ρ₂ ≈ ρ_h and ρ₁ ≈ ρ_e for long horn-antennas.

Now, to realize the physical horn- antenna, P_e and P_h must be equal.

We know that,

P_e = (b₁ – b) [ (ρ_e / b₁)² – ¼]^1/2

P_h = (a₁ – a) [ (ρ_h / a₁)² – ¼]^1/2

Now, we can rewrite the equation (1) as below.

[√ (2χ) – b/ λ]² (2χ -1) = [{(G₀ /2π√χ) * √ (3/2π)} – (a/ λ)]² * [(G₀² / 6π³χ) – 1] — (2)

Where,

ρ_e / λ = χ and,

ρ_h / λ = G₀² / 8π³χ

Equation (2) is known as the horn- antenna design equation.

Directivity of Horn Antenna

Before we step into finding out the directivity of a horn-antenna, let us know the directivity of an antenna? An antenna’s directivity is defined as the ratio of radiation intensity of an antenna in a particular direction to the averaged radiation intensity over all the directions. Directivity is considered as a parameter for calculating the figure of merit of the antenna.

The following mathematical expression describes the directivity.

D = U / U₀ = 4πU / P_rad

When the direction is not given, the default direction is the direction of maximum radiation intensity.

D_max = D₀ = U_max / U₀ = 4πU_max / P_rad

Here, ‘D’ is the directivity, and it has no direction as it is a ratio. U is the radiation intensity. U_max is the maximum radiation intensity. U₀ is the radiation intensity of the isotropic source. P_rad is the total radiated power. Its unit is Watt (W).

As earlier said, the horn-antenna is of three types. All the classes have different directivity. Let us discuss all of them.

E-Plane Sectoral Horn

The following expression gives the directivity of the E-Plane horn-antenna.

D_E = 4πU_max /P_rad = (64aρ₁ * | F(t) | ²)/πλ b₁

Where, | F(t) | = [C²b₁ / √ (2λρ₁) + S²b₁ / √ (2λρ₁)]

H-Plane Sectoral Horn

The following expression gives the directivity of the H-plane sectoral horn-antenna.

D_H = 4πU_max /P_rad = [4πbρ₂ /a₁ λ]* {[ C(u) – C(v)]² + [S(u) – S(v)]²}

Where,

u = (1/√2) * [{√ (λρ₂)/a₁ + a₁/ √ (λρ₂)}]

v = (1/√2) * [{√ (λρ₂)/a₁ – a₁/ √ (λρ₂)}]

Pyramidal Horn Antenna

The directivity of pyramidal horn- antenna depends on both the directivity of E & H plane sectoral horn. The equation is given below.

D_P = 4πU_max /P_rad = [8πρ₁ρ₂ /a₁b₁] * {[ C(u) – C(v)]² + [S(u) – S(v)]²} * {[C²b₁ / √ (2λρ₁) + S²b₁ / √ (2λρ₁)]}

It can be written as –

D_P = [π λ² / 32ab] * D_ED_H

Horn Antenna Radiation Pattern

Radiation Pattern is the angular dependence of the strength of the radio waves from any electromagnetic source. The below image shows the radiation pattern of a pyramidal horn-antenna.

Horn Antenna Gain

An antenna’s gain would refer to as the ratio of the intensity in a particular direction to the radiation intensity if the antenna were radiated isotopically. It is an essential parameter for measuring an antenna’s performance and has a close relationship with the antenna’s directivity. The gain of a horn- antenna lies around 25 dBi and the range is typically 10 – 20 dBi.

Horn antenna beamwidth

Antenna bandwidth is the angular distance between two matching points on the reverse side of the outline supreme. The horn-antenna beamwidth gets decreased if the frequency of the process gets increased.

The bandwidth of a practical horn-antenna stays in a range of 10:1 to 20:1.

Few mathematical problems related to Horn Antenna

1. Find the directivity of the E-plane sectoral horn-antenna. The details for the antenna are given below. a = 0.5λ, b = 0.25λ, b₁ = 6λ, ρ₁ = 6λ

Solution:

b₁ / √ (2λρ₁) = 6λ / √ (2λ*6λ) = 6 / √12 = 1.73

Now, [C (1.73)]² = (0.32)² = 0.1024 [from the chart of Fresnel integrals]

And, [S (1.73)]² = (0.54)² = 0.2916 [from the chart of Fresnel integrals]

We know that, D_E = 4πU_max /P_rad = (64aρ₁ * | F(t) | ²)/πλb₁

Where, | F(t) | = [C²b₁ / √ (2λρ₁) + S²b₁ / √ (2λρ₁)]

D_E = [{64 (0.5) * 6 * (0.1024 + 0.2916)} / 6π]

Or, D_E = 4.01 dB.

So, the directivity of the given E-Plane Sectoral Horn-Antenna is 4.01 dB.

2. Find the directivity of the H-plane sectoral horn-antenna. The details of the antenna are given below. a = 0.5λ, b = 0.25λ, a₁ = 6λ, ρ₂ = 6λ

Solution:

We know that,

u = (1/√2) * [{√ (λρ₂)/a₁ + a₁/ √ (λρ₂)}]

v = (1/√2) * [{√ (λρ₂)/a₁ – a₁/ √ (λρ₂)}]

Now, u = (1/√2) * [{√ (6)/6 + 6/ √ (6)}] = 2.02

And, v = (1/√2) * [{√ (6)/6 – 6/ √ (6)}] = – 1.44

Using Fresnel integrals,

C (u) = C (2.02) = 0.48825

C (v) = C (-1.44) = -C (1.44) = – 0.54310

S (u) = S (2.02) = 0.3434

S (v) = S (-1.44) = -S (1.44) = – 0.71353

We know that directivity of H-plane sectoral horn- antenna is 

D_H = 4πU_max /P_rad = [4πbρ₂ /a₁ λ]* {[C(u) – C(v)]² + [S(u) – S(v)]²}

Or, D_H = [4π (0.25)6/6] * [ (0.488 + 0.543)² + (0.343 + 0.713)²]

Or, D_H = (3.141) * (1.0629 + 1.1151)

Or, D_H = 6.84 dB

So, the directivity of the given H-plane Sectoral Horn-Antenna is 6.84 dB.

3. Designing details of a pyramidal horn-antenna is given below. ρ₂ = 6λ = ρ₁ = 6λ; a = 0.5λ, b = 0.25λ; a₁ = 6λ = b₁ = 6λ; Check if a practical horn-antenna can be designed with those details. Also, find out the directivity of the pyramidal horn- antenna.

Solution:

            Now, ρ_e = λ √ ([6²+ (6 / 2)²] = 6.708λ

            And, ρ_h = λ √ ([6²+ (6 / 2)²] = 6.708λ

We know that,

P_e = (b₁ – b) [ (ρ_e / b₁)² – ¼]^1/2

P_h = (a₁ – a) [ (ρ_h / a₁)² – ¼]^1/2

Now, P_e = (6λ– 0.25λ) [ (6.708 / 6)² – ¼]^1/2 = 5.74λ

And, P_h = (6λ– 0.5λ) [ (6.708 / 6)² – ¼]^1/2 = 5.12λ

As we can see, P_e is not equal to P_h, so the design is not possible to implement.

            We know that the directivity of a pyramidal horn-antenna is 

D_P = [π λ² / 32ab] * D_ED_H

            Now, D_P = [π / 32 * (0.5) * (0.25)] * 6.84 * 4.01]

            [The value of D_ED_{H is} has been calculated previously]

            Or, D_P = 21.54

            Converting it to the dB value, D_P = 10log21.54 = 13.33 dB

So, the directivity of the given Pyramidal Horn-antenna is 13.33 dB.

Cover Image Credit – Sajad-HasanAhmadi, TV antenna connectors, CC BY-SA 4.0

Points of Discussion: Transmission Line

• Introduction
• Purpose of transmission line
• Analysis of transmission line
• Types of transmission line
• Applications of transmission lines

Introduction to Transmission Line

A transmission line is a specially designed cable for transmission of power. It conducts only electromagnetic waves to the load at low frequencies in a guided way.

            Transmission line operates at microwave frequency domain and radio frequency domain where power is assumed as an electromagnetic wave. That is why if any cable can guide an electromagnet signal, then it will be called a Transmission line.

            The transmission line is the result of researches of James Maxwell, Lord Kelvin, and Oliver Heaviside. The fault and drawbacks of the ‘Atlantic telegraph cable’ and invention of telegrapher’s equation made the way out for the line.

Purpose of transmission line

Regular cables which transfer electrical energy are designed to conduct power at lower frequency AC. They cannot carry power in FR range or above 30 kilo hertz as the energy gets disconnected at joints and connectors, and some time does not reach the destination. This lines resolve these problems. They are constructed specially to minimize the reflections and loss of power and also uses the impedance matching to carry power.

            This lines are constructed with a uniform cross-sectional area. That is why they provide uniform impedance which is in terms known as characteristic impedance.

            The wavelength of the electromagnetic waves gets shorter as the frequency gets higher of the electromagnetic waves.  Transmission lines are crucial because when the wavelength is short enough, the length of the wire contributes to the past of the wavelength.

What is a Yagi Uda Antenna? Click here for details!

Analysis of Transmission line

            We assume a four-terminal model of the transmission lines to analyze the construction and working of lines. It is equivalent to a typical two-port circuit. 

            We assume that the circuit is linear, which means that the complex voltage at any port is relational to the complex current for the reflectionless condition. Also, we assume that two of its ports are transposable.

Characteristics impedance of transmission line

Characteristic impedance or (Z0) is an essential parameter of the line. It can be defined as the ratio of the magnitude of the voltage to the magnitude of the current of a wave, travelling along a reflection less line.

Characteristics impedance controls the behaviors of the line only if the line is uniform in length. Generally, for co-axial cables, characteristic impedance has a value of fifty to seventy ohms, and for warped pair of wires, the value is 100 ohms. For untwisted pair, the value is 300 ohms.

Transmission line reflection coefficient

The line’s reflection coefficient is given by the ratio of the complex magnitude of the reflected signal to the incoming signal. It is represented by the Greek alphabet – Г and expressed as –

It has a relation with the load impedance and characteristic impedance. The expression is given below.

The standing wave ratio also has a relation with this line reflection coefficient. The connection is given as –

Matched condition of transmission line:

The aim of a transmission line is to deliver the maximum power from the source to destination load and to minimize the reflection and loss of the power. The ‘matched’ condition can fulfil this desired. If the destination’s load impedance is made same or equal to the value of the characteristic impedance of the line, then the line achieves ‘matched’ condition.

            Instead of the ‘matched’ condition, the transmission suffers some loss. Like, ohmic loss. There is also another substantial loss that occurs when this line works in high frequency ranges. The loss is known as dielectric loss. Here, the inside elements of this lines, grips the EM energy and produces heat.

            The aggregate loss of this line is measured by the unit dB/m. The losses are dependent on the frequency of the signal, as mentioned earlier. The constructor companies of this usually provide a chart of loss. It shows the loss of power at different frequencies. If any line suffers a loss of three decibel/meter, then the power received at the load will be half of the power supplied.

What is horn antenna? get an overview here!

Types of transmission lines

 These come with certain types depending upon its physical structure and according to the needs. Some of the essential and widely used types of transmission lines are listed below. Please go through it and discover them.

Co-axial cables:

It is one of the widely used forms of lines. It restricts the whole EM wave inside the cable. Thus, co-axial cables can be bent, strapped as well as twisted to an extent without affecting the operation.

EM waves promulgate in TEM or transverse electric and magnetic mode For the RF range applications. Here, both the electric and magnetic fields are perpendicular with the promulgate directions. The electric field becomes radiated, and the magnetic field becomes circumferential.

If the wavelength of the wave is shorter than the circumference of the co-axial cable, then the TEM gets divided into two. The modes are then known as TE or transverse electric and TM or transverse magnetic.

Co-axial cables have broad applications for televisions. It was primarily used for telephones in the middle of twenty century.

Microstrip transmission lines:

A microstrip network is basically a tiny conductive plane, placed parallelly to the ground surface. It can be designed by putting a thin and flat metallic plane on the side of a PCB. The opposite surface must be the ground plane. The characteristic impedance of the microstrip type line depends on that conductive strip. The height, width, dielectric coefficient of the conductive strip provides the characteristic impedance. A point to be remembered that the microstrip type line is an open structure while the co-axial cable is a closed one.

Twisted pair transmission lines:

In this type of line where pairs of wire are assembled together to form a single chain or a cable is known as tangled pair transmission lines. These types of lines are used in global telephonic communications. Also, it has used in data circulation inside buildings. This type is not economical due to its properties.

Star quad:

Star quad is another wire-combinational formation. It uses four cables, and all the conductors of the four cables are twisted and assembled along the axis of the cable. In this formation, each and every pairs uses a far pair to get connected.

The combinational form of twisted, balancing and quadrupole pattern of transmission lines has several benefits as it reduces noise, particularly for short signal level usage like – cables of the microphone.

This type of line has applications in four-wire telephony, two-wire applications.

It also induces high capacitance which further causes distortion and losses.

Applications of transmission lines | Uses of transmission lines

Transmission lines have several benefits over regular electrical cables in specific domains. That is why it has several applications. Let us discuss some of them.

• Electromagnetic powers are supplied in high frequency domains with minimum loss. Tv and radio cables for connecting the aerials is one of the most famous examples.
• These are also used for the generation of pulses by charging and discharging this lines. A significant example of this type of line is – Blumlein Transmission Line. Radars have also multiple application of this kind.
• These are also applied in stub filters. Stub filters are typically wired in a parallel connection and transfer power from the source to destinations.

Check out more on Electronics! Click Here!

VLSI, VHDL, Verilog Interview Questions

1. Give the full term of VHDL.

1. Very High Definition Language
2. Very High Speed Integration Hardware Description Language
3. Very High Description Language
4. Very High Speed Scaling Hardware Describing Language

Ans: 2) Very High Speed Integration Hardware Description Language

For basic VHDL Tutorials, Click Here!

2. What is the number of Metal Oxide Filed Effect Transistors are needed to construct a Bi-complementary metal Oxide Semiconductor NOR gate which have two input?

1. 5 MOSFETs
2. 6 MOSFETs
3. 7 MOSFETs
4. 8 MOSFETs

Ans: 3) 7 MOSFETs

“How a Logic gate is designed in VLSI?” Find the answer here!

3. What is the effect of ‘Delay’ if the power supply voltage gets increased?

1. Increases
2. Decreases
3. Remains the same
4. Delay has nothing o do with power supply.

Ans: 2) Decreases

4. Which is true about VLSI design?

1. VLSI is a sequential process which has feedback loops.
2. VLSI is a parallel process which has no feedback loops.
3. VLSI is both sequential and parallel process that has feedback loops.
4. VLSI is a sequential process which has no feedback loops.

Ans: 3) VLSI is both sequential and parallel process that has feedback loops.

For more details about Verilog Interview Questions and other topic like VLSI Design, Check this!

5. What is the use of CAD tools in VLSI design?

1. It automates the VLSI design.
2. It reduces the design cycle time.
3. It reduces the chance of errors.
4. All of the above.

Ans: 4) All of the above.

6. Which type of product is more suitable for FPGA based Design?

1. Large scale product development.
2. High Speed applications.
3. Prototype development.
4. Low power applications.

Ans: 3) Prototype development.

What is Verilog? What is system Verilog? and other Verilog Interview Questions and Answers are here!

7. What is the relation between interconnect delay and gate delay?

1. The Relation is technology dependent.
2. Gate delay always more than interconnect delay.
3. Interconnect delay always more than the gate delay.
4. They are same.

Ans: 1) The relation is technology dependent.

8. State True or False

Statement: For a Y chart, the details of design information increases when moved from the centre to the periphery.

1. True
2. False

Ans: (2). False

9. Why a short channel device is preferred?

1. It is easier for fabrication.
2. It has lower power consumption.
3. It has high speed.
4. It has better output characteristics.

Ans: 3) It has high speed.

10. Where does the subthreshold operation of MOSFET find applications?

1. Memories.
2. Charge coupled devices.
3. Biomedical applications.
4. None of the above.

Ans: 3) Biomedical applications.

11. What is the relation between the ON-resistance of MOSFET and gate to source voltage (Vgs)?

1. ON-resistance linearly increases with Vgs.
2. ON-resistance linearly decreases with Vgs.
3. ON-resistance exponentially increases with Vgs.
4. ON-resistance non-linearly decreases with Vgs.

Ans: 4) ON-resistance non-linearly decreases with Vgs.

12. What is the threshold voltage of an EMOSFET?

1. Equal to 0 V.
2. Less than 0 V.
3. Greater than 0 V.
4. None of the above.

Ans: 3) Greater than 0 V.

13. Find the odd one out.

1. Channel length modulation
2. Subthreshold Conduction
3. Hot carrier effect.
4. Body Effect

Ans: 4) Body effect. (All the other options are 2^nd order effect).

14. How does doping density change for constant voltage scaling?

1. Increases by a factor of s
2. Increases by a factor of s2.
3. Decreases by a factor for s.
4. Decreases by a factor for s2.

Ans: 2) Increases by a factor of s2.

15. How does power dissipation occur for full scaling?

1. Increases by a factor of s
2. Increases by a factor of s2.
3. Decreases by a factor for s.
4. Decreases by a factor for s2.

Ans: 3) Decreases by a factor of s2.

16. How does power dissipation occur for constant voltage scaling?

1. Increases by a factor of s
2. Increases by a factor of s2.
3. Decreases by a factor for s.
4. Decreases by a factor for s2.

Ans: 1) Increases by a factor of s.

17. What is the main advantage of depletion load NMOSFET inverter over EMOSFET load?

1. Less power dissipation
2. Easier fabrication process
3. Sharper Vtc transitions and better noise margins.
4. None of the above.

Ans: 3) Sharper Vtc transitions and better noise margin.

18. Why is polysilicon used for the gate in MOSFET?

1. Because it is a semi-metal.
2. Because it has lattice matching with Silicone
3. Because it is easier to fabricate.
4. None of the above.

Ans: 2) Because it has lattice matching with silicone.

19. State True or False

Statement: In full scaling, the magnitude of the electric field is constant.

1. True
2. False

Solution: (1). True

20. Which of the given statement is true regarding a MOSFET inverter?

1. One PMOSFET and one resistor are needed to implement a MOSFET inverter.
2. One NMOSFET and one resistor are needed to implement a MOSFET inverter.
3. Two PMOSFETs.
4. Two NMOSFETs.

Ans: 2) One NMOSFET and one resistor is needed to implement a MOSFET inverter.

21. On which factors, the power dissipation of a CMOS inverter depends?

1. Supplied Voltage.
2. NMOSFET’s channel width.
3. PMOSFET’s channel width.
4. All of the above.

Ans: 1) Supplied Voltage

22. State True or False

Statement: The PMOS transistors act as Pull-up network in a CMOS inverter.

1. True
2. False

Solution: (1). True

23. Which of the following effect has no contribution to deviate the ideal situation of a current mirror circuit?

1. DIBL effects.
2. Threshold offset between two transistors
3. Channel length modulation
4. Imperfect geometrical matching.

Ans: 1) DIBL effects.

24. What does the ASIC cell library contain?

1. The physical layout of the cells
2. Routing model of the cells
3. Timing model of the cells
4. All of the above.

Ans: 1) Physical layout of the cells.

25. Why does lowest propagation delay occur through a gate?

1. Due to – strong transistor, high temperature, high voltage.
2. Due to – strong transistor, low temperature, high voltage.
3. Due to – Weak transistor, high temperature, high voltage.
4. Due to – weak transistor, low temperature, low voltage.

Ans: 3) Due to – Weak transistor, high temperature, high voltage.

26. Which of the following is true about VLSI logic design?

1. VLSI minimizes the area and delay
2. VLSI minimizes the area at the cost of delay
3. VLSI maximizes speed by decreasing area
4. VLSI minimizes delay by reducing the area

Ans: 2) VLSI minimizes the area at the cost of delay.

27. What is a hard macro?

1. Flexible Block
2. Fixed Block
3. Flexible block with a fixed aspect ratio
4. Flexible block with a flexible aspect ratio

Ans: 2) Fixed Block

28. State True or False

Statement: The full form of SPICE is – Simulation Program with Integrated Circuit Emphasis.

1. True
2. False

Solution: (1). True

29. What is the equivalent circuit for CMOS comparator?

1. Uncompensated CMOS OPAMP.
2. Compensated CMOS OPAMP.
3. Partially Compensated CMOS OPAMP.
4. None of the above is true.

Ans: 1) Uncompensated CMOS OPAMP.

30. What is the relation between the equivalent resistance of a switched capacitor and the clock frequency?

1. The resistance is proportional to clock frequency.
2. The resistance is inversely proportional to clock frequency.
3. The resistance is proportional to the square of the clock frequency.
4. The resistance is inversely proportional to the square of the clock frequency.

Ans: 2) The resistance is inversely proportional to clock frequency.

31. What is the relation between the equivalent resistance of a switched capacitor and the capacitance?

1. The resistance is proportional to the capacitance.
2. The resistance is inversely proportional to the capacitance.
3. The resistance is proportional to the square of the capacitance.
4. The resistance is inversely proportional to the square of the capacitance.

Ans: 2) The resistance is inversely proportional to the capacitance.

32. What is the condition for domination by Diffusion Current?

1. Strong Inversion
2. Weak Inversion
3. Both Strong and weak inversion.
4. Cannot be determined.

Ans: 2) Weak Inversion.

33. What is the condition for domination by Drift Current?

1. Strong Inversion
2. Weak Inversion
3. Both Strong and weak inversion.
4. Cannot be determined.

Ans: 1) Strong Inversion.

34. State True or False

Statement: In the cascode current mirror, the output resistance is increased.

1. True
2. False

Solution: (1). True

35. State True or False

Statement: A current mirror circuit can be used as a current amplifier by increasing the (W/L) ratios of the mirrored and source MOSFET

1. True
2. False

Solution: (1). True

36. Which connections of NMOS in PDN, help to realize the AND terms?

1. Cascade Connection
2. Anti – parallel Connections
3. Series Connections
4. Parallel Connections

Ans: 3) Series Connections

37. Which type of transistor can pass logic-high value perfectly, but not the logic-low value?

1. NMOSFET
2. PMOSFET
3. CMOS
4. None of the above

Ans: 2) PMOSFET

38. What is the minimum number of transistors needed to design an XOR gate?

1. Three
2. Four
3. Five
4. Six

Ans: 4) Six

39. Which type of logic design provides the minimum propagation delay?

1. Emitter Coupled Logic
2. Transistor Transistor Logic
3. Register Transistor Logic
4. Diode Transistor Logic

Ans: 1) Emitter Coupled Logic

40. State True or False

Statement: Dynamic CMOS logic operates using two non-overlapping clock pulses.

1. True
2. False

Solution: (2). False.

For more VLSI related topic and Verilog interview questions click here

Topics for Discussion

A. Xilinx

B. Prerequisites for Verilog HDL Using Xilinx

C. Xilinx Installation process

D. Creating your first Verilog project with XILINX

XILINX

Xilinx is a USA based tech-company which provides programmable logic devices. We will use Xilinx’s software “ISE 14.7 Simulator to implement Verilog designs. Xilinx is also used for VHDL implementations. Though some of the coding structure of Verilog is same as VHDL, there are fundamental differences between them.

First of all learn Verilog! Click Here!

Prerequisites for Verilog using Xilinx

Before getting started with Verilog with Xilinx, there are some prerequisites for an user. They are listed below.

• Must have some knowledge of digital electronics. At least bits of knowledge of basic logic gates and sequential circuits are required.
• An uninterrupted internet connection is a must.
• A healthy amount of free memory is required to run the software smoothly. At least 20 GB space is needed in your machine.
• Create an account on Xilinx’s website with an accessible email-id. The license will be mailed in that email-id.
• We are demonstrating this tutorial for windows only.   

What is VHDL? What is the difference between Verilog & VHDL?

Xilinx Installation Process

• Step 1: Download the software from the internet. The link to download Xilinx is given below –

(It is a 6GB ZIP file, ensure internet connection and space) The link for windows –

https://www.xilinx.com/member/forms/download/xef.html?filename=Xilinx_ISE_DS_Win_14.7_1015_1.tar

There are other downloadable options available. You can choose according to your requirement and choice from the below given link.

https://www.xilinx.com/support/download/index.html/content/xilinx/en/downloadNav/vivado-design-tools/archive-ise.html

• Step 2: Unzip the file. To unzip the file, right-click on the file, and there will be an option to extract all. After the extraction, the file name should be – ‘Xilinx_ISE_DS_Win_14.7_1015.1”.

Point to be noted – Both the download and extraction will need a lot of time depending upon internet speed and storage availability. The installation will require a lot of time too. So, don’t panic, be patient.

• Step 3: Open the extracted file. There is a file named – ‘xsetup’. Double click on that file. It will start the installation.

1. There will be another pop-up, choose the ‘ISE WebPACK’ option to continue.

It will start the final installation process.

• Step 4: After the software gets installed in your PC, some tasks must be performed. Do these tasks carefully. Also, update the license from Xilinx. Those steps are given in the previous article; please check it out before we start with our first Verilog Project. The link is given below.

https://lambdageeks.com/vhdl-process-xilinx-guide/

Creating your first Verilog project with XILINX

We will first implement a simple AND gate model using XILINX. The logical representation of AND gate is Y = AB; A and B are the two inputs, while Y is the output. The truth table is given below.

A	B	Y =AB
0	0	0
0	1	0
1	0	0
1	1	1

• Step 1: Open the project navigator by double clicking the icon on the desktop.
• Step 2: Go to ‘File’ and then ‘New Project’. File -> New Project

• Step 3: Type a name for your project and select the storage location. It is advised not to use basic logic gate names as they are reversed keywords. Also, don’t forget to copy the name of your project; it will help your letter. Click on the ‘Next’ button to proceed.

• Step 4: Now, you have to set up a few things. Be careful while setting up all these things. Any mistake will lead to failure in the long-term result.

• Property Name: Value
• Evaluation Development Board: None Specified
• Product Category: All
• Family: Spartan3
• Device: XC3S50
• Package: PQ208
• Speed: -4
• Top Source Type: HDL
• Synthesis Tool: XST (VHDL/Verilog)
• Simulator: lSim (VHDL/Verilog)
• Preferred Language: Verilog
• Property Specification in Project File: Store all values
• Manual Compile Order: Leave the checkbox, don’t click on it.
• VHDL Source Analysis Standard: VHDL-93
• Enable Message Filtering:  Leave the checkbox, don’t click on it.

Click on ‘Next’ to proceed.

• Step 5: Now, click on ‘Finish; for the next pop-up.

• Step 6: A new window will be opened up in the ISE simulator. Inside the design tab at the left corner, and under the Hierarchy bar, the model will have appeared. Move your cursor on the folder just below the named model.

Then right-click on the folder (in our case the name of the folder is – ‘xc3s50-4pq208’). Then, select the new source.

• Step 7: In the new window, choose the ‘Verilog Module’ and paste the same name you have copied in the step 3. You can also get that name from the location tab. Click on ‘Next’ to proceed.

• Step 8: The defining module will come up. But we will not define the ports now. Just click on ‘Next’.

• Step 9: Click on “Finish” for the next window pop-up.

• Step 10: A code editor will be opened up.
  • Now change the project name written in the editor to “AND”. For our case, we change it from ‘LAMBDAGEEKS_VERILOG_AND_GATE’ to ‘AND’.

• Now write down the port declarations as follow.

module AND (

                        input I1, I2,

                        output O

                        );

endmodule

• Now assign the AND gate in-between the input and output.

assign O = I1 & I2;

• Save the code.
• Step 11: Now, on the left side of the window, under the design bar, you can see a tab named “Process AND”.
  • Expand the ‘Synthesis – XST’ from there.
  • Double click on the ‘Check Syntax’. It will show a green tick, denoting success.

• Step 12: Now again go back to the top-left section. Right-click  on the ‘xc3s50-4pq208’ file. Choose a new source from there.

• Step 13: Choose Verilog Module from the given list. Then put a file name. We put “LAMBDAGEEKS_TOP_MODULE” as the name. Click on the ‘Next’ to proceed.

1. A pop-up named ‘Define Module’ will come. Do not define anything here. Click on the ‘Next’.

• Click on ‘Finish’ for the next popped-up window.

• Step 14: A code editor will be opened up. You can erase all the comment section from the code editor.
  • Now, check the Hierarchy Section at the top left. Right-click on the Module Name given by you. For our case, it is – ‘LAMBDAGEEKS_TOP_MODULE’.
  • Some options will come upon the right click. Choose the option – ‘Set as Top Module’.

• A window will pop-up. Click on ‘YES’ to continue.

• Step 15: Now, we have to write some code using the code editor. It describes the input and output with the gate implementation. The following code is written for AND gate –

module LAMBDAGEEKS_TOP_MODULE(

            input I1, I2,

            output O

  );

            AND and1(I1,I2,O);

endmodule

• Step 16:  Now go to the left down part at ‘Process: LAMBDAGEEKS_TOP_MODULE’ section.
  • Now Expand the ‘Synthesis -XST’ part.
  • Double click on the ‘Check Syntax’. It will show a green tick denoting success after a few seconds.
  • Then, Double click on the ‘Synthesis – XST’ option. It will take a few seconds to show a green tick.

• Step 17:  View for RTL Schematic.
  • Double click on the ‘View RTL Schematic’ option.
  • A window named – ‘Set RTL/ Tech Viewer behaves when it is initially invoked’ will pop up. Just click on the ‘OK’.

• Now a window will be opened with a diagram.

• Double click inside the box.

• Now, double click inside the AND box.

• Step 18: View for Technology Schema
  • Double click on the ‘View technology Schematic’ option.
  • A pop-up will come to click on the ‘OK’ option.

• A new diagrammatic window opened up.

•  Double Click inside the box of the diagram.

• A box will be there named – ‘lut2’. Double click on that.

It will display several diagrams.

The schematic Diagram:

• Click on the Equation to see the relation.

• Click on the Truth table to find the truth table.

• Click on the Karnaugh Map to find the Map.

Check out our other VLSI articles!

• 1. VLSI Basics
• 2. VLSI logic Design(Advanced)
• 3. Frequently Asked Interview Questions on VLSI!

Verilog Tutorial : Points of Discussion

• What is Verilog?
• History and Standardization
• Verilog Design
• Verilog Modelling
• Verilog Operators

For others topic related to Verilog Tutorial, Click Here!

What is Verilog?

Verilog is the combination of the terms “Verification” and “Logic”. It is hardware description language or a special type of programming language which describes the hardware implementations of digital system and circuits. It is a strongly typed language and points to be remembered that it is not a programming language.

For step-by-step VHDL Tutorial, Click Here!

History and Standardization of Verilog

Prabhu Goel, Chi-Lai Huang, Douglas Warmke and Phil Moorby developed the Verilog around the year 1983-1984. The first name was “Automated Integrated Design Systems” which was further renamed as “Gateway Design Automation” and was purchased by Cadence in the year 1990. Cadence is now the copyright owner of Verilog and the Verilog-XL.

Primarily, the use of Verilog was to define and to start the simulation. Later the popularity of the language raised a demand for more development, and it leads to the synthesis of the logic circuits.

Verilog Tutorial: Standardization

The popularity for VHDL forced cadence to publish the Verilog Language as open source. The first standardization of Verilog by IEEE was labelled as 1364-1995 and named as Verilog-95.

Revisions	Updates
IEEE 1364 – 2001	Verilog-2001. Supports signed variables and nest. Largely used by EDA packages.
IEEE 1364-2005	Verilog 2005. Came up with little corrections and clarifications.
IEEE P1800-2005	System Verilog.
IEEE 1800-2017	Merger of SystemVerilog and Verilog. Known as SystemVerilog 2009.

Verilog Design

Verilog has two types of design methodologies. They are – Bottom-up approach & Top-down approach.

Bottom-up Approach: It is the conventional way of designing models. The planning is implemented at the gate level. Typical gates are used for implementations. This method opens up paths for different structural and ordered planning.

Top-down Approach: This approach has some advantages over the conventional one. Changes can be made easier here. Early testing is also possible.

Verilog Modelling

Verilog modelling has some design units. Let us discuss the primary components.

A. Module

A Verilog model comes up with port declarations, data type declarations, circuit functionality, timing specifications. A basic structure of the Module is given below.

• Verilog is case sensitive.
• Reserved keywords are written in lower cases.
• A semicolon is used to terminate the statement.
• The comment rule is same as C Programming Language.
• Single line comment starts with “//”.

For example – //Example of a Verilog single line comment

• Multiline comments start with – ‘ /*’  and ends with ‘*/’.

For example –

/* Example

Of Verilog multiple

Line comment*/

• Timing specifications are used for the simulation process.

A module consists of a maximum of four levels of notion. The levels are defined below.

Behavioral: The highest level of notion. The anticipated design is planned at this level. Though, there is no thought for hardware implementations.

Dataflow: This level of Verilog Module describes the dataflow of the desired design. Hardware implementations of the dataflow through components are kept in mind while designing this level.

Gate: Logic gates are implemented in this Verilog module level. Interconnections are implemented between the gates.

Switch: The lowest level of notion. Switches, storage lumps are implemented. The interconnections are also designed between them.

B. Module Declarations

Module declarations start with ‘module’ keyword. It includes a port list (if exists).

Port types: There are three types of ports. The name and its functionality are given below.

• input – input port
• output – output port
• inout – bi-directional port

Port Declarations: The general structure for port declarations is given below.

<port_type> <port_name>;

C. Data Types

There are several kinds of data types in Verilog.

 Net Data Type: This type of data describes the physical interrelate between flows.

Nets -> Functional Block: MUX -> Functional Blocks: Adders -> Nets

The below table will provide more details about Net Datatype.

Type	Characterization
wire	Describes node or connections
tri	Describes a tri-state node
supply0	Represents Logic 0
suppy1	Represents Logic 1

•  Bus declarations: The general structure of bus declarations is given below.

<data_type> [Most Significant Bit (MSB): Least Significant Bit(LSB)] <signal_name>;

          <data_type> [Least Significant Bit(LSB): Most Significant Bit(MSB)] <signal_name>;

For example –

wire [3: 1] in;

Variable Data Type: This datatype describes the element to save a data for the time being.

There are many types of variable, supported by Verilog. Some of them are –

integer – 32 bits, Signed.

reg – any bit size, unsigned. To implement signed reg, use keyword – ‘reg signed’.

real, time, realtime – no support for synthesis.

D. Module Instantiation

After all the declarations, the module can be instantiated at a higher-level module with the help of some syntaxes. By instantiating modules, we can build designs with multiple levels of hierarchy. That will further help us to achieve simpler maintainability. Most of the modern designs have numerous layers of hierarchy.

The general format for instantiation is given below.

<componenet_name> #<delay> <instance_name> (port_list);

component name: It is the name of the module for the lower-level component.

delay: It is an optional choice. Delay introduces a delay throughout the component.

instance name: It is the exclusive name given by the designer for every individual instance.

port list: Port list gives the signal lists which will be connected to the component.

E. Simulation Component

After the designing process get completed, the testing process starts. This testing can be done using the stimulus block. Stimulus blocks are commonly known as a test bench.

Stimulus applications can be of two types. The primary design starts with the design block and directly drags the port signals into the design blocks.

The second design instantiates the stimulus block and the design block in a higher-level replica model. Interface is the communication link between the blocks.

Some Basic Verilog Concepts

Verilog Operators

Verilog has three fundamental operators for Verilog HDL. They are given below.

Unary Verilog operators : These types of Verilog operators come first of the operands.

For example: x = ~ y; Here ‘~’ is a unary operator

Binary Verilog operators : These types of Verilog operators come in-between two operands.

For example: x = y || z ; Here ‘||’ is a binary operator.

Ternary Verilog operators : These types of Verilog operators use two different operators to differentiates three operators.

For example: x = y?  z  : w; here ‘?’ and ‘:’ are ternary operators.

Verilog HDL’s categorical operators are – arithmetical, logical, relational, bitwise, shift, concatenation, and equality. Different types of Verilog operators and their symbols are given in the below table.

Type of Operator	Symbol	Operation	Operands needed
Arithmetic	*	Multiplication	Two
Arithmetic	/	Division	Two
Arithmetic	+	Addition	Two
Arithmetic	–	Subtraction	Two
Arithmetic	%	Modulus	Two
Logical	!	negation	One
Logical	&&	AND	Two
Logical	||	OR	Two
Relational	>	Greater than	Two
Relational	<	Less than	Two
Relational	> =	Greater than or equal to	Two
Relational	< =	Less than or equal to	Two
Equality	==	Equals to	Two
Equality	! =	Not equals to	Two
Equality	===	Case equal	Two
Equality	! ==	Case not equal	Two
Bitwise	~	Negation	One
Bitwise	&	Bitwise AND	Two
Bitwise	|	Bitwise OR	Two
Bitwise	^	Bitwise XOR	Two
Bitwise	~^	Bitwise XNOR	Two
Reduction	&	Reduction AND	One
Reduction	~&	Reduction NAND	One
Reduction	|	Reduction OR	One
Reduction	~|	Reduction NOR	One
Reduction	^	Reduction XOR	One
Reduction	^~	Reduction XNOR	One
Shift	>>	Right Shift	Two
Shift	<<	Left Shift	Two
Concatenation	{ }	Concatenation	Can be of any numbers
Replication	{ { } }	Replication	Can be of any numbers
Conditional	? :	Conditional	Three

Verilog Operators has precedence also. Their Precedence is given in the below table.

Operator	Symbols	Precedence
Unary Multiplication, Division, Modulus	+ ,-, !, ~ *, /, %	Highest
Addition, Subtraction Shift	+, – <<, >>
Relational Equality	<, <=, >, >= ==, !=, ===, !==
Reduction     Logical	&, ~& ^, ^~ |, ~| && ||
Conditional	?:	Lowest

Verilog Number Specifications

Verilog numbers are of two types, sized numbers and unsized numbers.

Sized Verilog numbers: The general structure for representing sized numbers in Verilog HDL is given below.

<size>’<base_format><numbers>

For example – 8’b3456;

This is a sized Verilog number which describes that it is an 8-bit number and of binary type.

• size: Size is the number of digits the main number has. Size is described using decimal values.
• base_format: Base format suggests which type of number it would be. There are several types – binary (given by – ‘b’), decimal (given by – ‘d’), octal (given by – ‘o’), hexadecimal (given by – ‘h’). If there is no specification for base_format, then by default it is a decimal number.
• numbers: The main number you want to put in.

Unsized Verilog numbers: These numbers do not require any specified size.

The general structure for representing unsized numbers in Verilog HDL is given below.

’<base_format><numbers>

For example – ’h3456;

This is an unsized Verilog number which describes that it is a hexadecimal number.

Negative Numbers: If you want to declare a number as a negative number, then put a minus symbol (-) before the number.

For example: – 345; it is a negative, unsized, decimal number.

Verilog Arrays

Arrays of integer, registers (reg), vectors ( of reg or net data types, several bit lengths) and time are possible in Verilog HDL. The basic declaration of arrays is shown below with an example.

integer matrix [0:3];

This means an array of seven values.

• Verilog doesn’t allow any array for real variables.
• Verilog HDL doesn’t support any multidimensional array.
• Array elements can be retrieved using – <array_name>[<position_of_the_element>]

For others topic related to Verilog Tutorial, Click Here!

For step-by-step Verilog Tutorial using Xilinx, Check our next article!