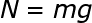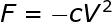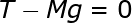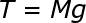Force

When two bodies come in contact -surfaces, a component acts upon them perpendicular to the contact surface. This is known as normal force.

Can normal force be at an angle:- The normal force exerted on the body tends to balance the gravity force (mg) on the body. As the normal force depends upon the value of force experienced by a body, but the normal force is always perpendicular to the body.

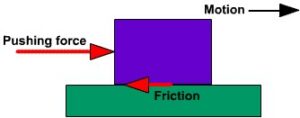
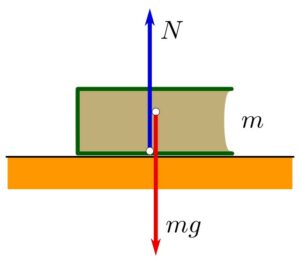
We need to understand the force exerted on a body. Let us take an example of a block that is at rest position on the table surface.

In this condition, the block experiences two types of forces.

• First is the gravity force (mg) which acts vertically downwards at the center of gravity of the block.
• Second is the reactionary force P which acts vertically upward. These forces are passing through the center of gravity of the block.

 Hence the block is in P= mg.

 Now, if we apply any external force F on the block, suppose in the right direction. In this condition, the block does not move. Instead, the force P ( vertically upward) is now inclined in the left direction. Here the force P acting on the block can be divided into two components. One will be parallel, and the other will be perpendicular to the contact surface.

Force of static friction this force balance the applied force F . in contrast, the force which is perpendicular to the block is known as normal force R . (R=mg).

The limiting frictional force is directly proportional to the normal force:-

f_sαR

The coefficient of limiting friction is the ratio of limiting frictional force to the normal force.

 When two surfaces are in relative motion, the force acting between them is known as kinetic frictional force fk. This is less than the limiting fraction, this is given as:-

fk=μkR

Where ,

μk<μs

To check whether “can normal force be at an angle” lets check it through the following conditions:-

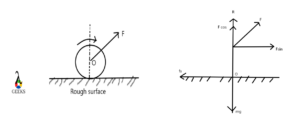
While pulling roller:-

When a roller of mass m is tried to pull over a horizontal surface by applying a force of F at an angle . As shown below in the figure:-

By considering that roller is in equilibrium, we say that:-

R₁+Fcosθ=mg

R₁=mg-Fcosθ

Here the coefficient of static friction between roller and surface   is,  then we can write f_s as:-

f_s=μ_sR1

f_s=μ_s(mg-Fcosθ)

Now we can say that normal force is perpendicular to the center of gravity of the roller.

When a roller of mass m is tried to push over a horizontal surface by applying a force of F at an angle. As shown below in the figure:-

R2=Fcosθ+mg

f_s‘=μ_sR2

f_s‘=μ_s(Fcosθ+mg)

In this condition also the normal force is perpendicular to the center of gravity of the roller.

From the given an example, while comparing Equations 1 and 2, we can say that it is easier to pull a roller rather than to push it because frictional force is less while pulling.

If we consider a case of rolling friction which is much less than sliding friction, in this case, also we find normal force at 90 degrees only.

As we know, the rolling friction is directly proportional to the normal force R. and inversely proportional to the radius r of the wheel.

f_rαR/r

f_r=μ_r*(R/r)

Where μ_r is the coefficient of rolling friction.

From all the given examples, we know that normal force is always perpendicularly upward to the center of gravity of the body.

Problem examples related to normal force:-

The force of 980 N is equal to the limiting frictional force. Hence the coefficient of static friction is:

μ_s=f_s/R

Where R is the normal force is equal to mg.

μ_s=980/(200*9.8)

μ_s=0.05

The angle of friction is given by;

tan θ_s=μ_s=0.05

θ_s=tan^-1(0.05)

• A block of mass 2kg is placed on the floor. The coefficient of static friction is 0.4. A force of 2.5 N is applied on the block, as shown. Calculate the force of friction between the block and the floor?

Let R be the normal force on the block exerted by the floor. The limiting force of static friction is:

f_s=μ_rR=μ_smg

0.4*2kg*9.8ms²

7.84N

• When a weight of a body placed on a surface is doubled,  how does the coefficient of friction change?

There is No change in the coefficient of friction. In fact, the force of the limiting fraction is doubled.

f_s=μ_sR=μ_smg

When we lubricate a body, then the lubricant form a thin layer around two surface. In such condition the sliding friction is replaces by liquid friction. Where liquid friction is less than sliding friction. this results in less friction.

• Can we jump off from a frictionless horizontal surface?

No, we can not jump off from a frictionless horizontal surface. Because a frictionless surface does not offer, normal reaction.

• What are the conditions on which the coefficient of friction between two surfaces depends?

The coefficient of friction depends upon the nature of both surfaces in contact, its evenness and the surface temperature.

Also Read:

• How to find normal force between two blocks
• Gravitational force examples
• How to find normal force with coefficient of friction
• Torque vs force
• Is net force a vector
• Gravitational force of moon
• How to find tension force in a pulley
• Electrostatic force examples
• Is gravitational force positive
• Atomic force microscopy imaging techniques

Force on moving charge in electric field is determined when a charged particle moves without acceleration it produces an electric field.

Firstly an electric field is created when two parallel plates are charged, otherwise called capacitors. When the test charges are placed between the charged capacitor plates they  move from the positive end to the negative end. Each such charge carries like this creating a line.

The test charges move from positive to negative side creating lines of force is called an electric field. Since these lines of charges form a uniform pattern, then there is said to be a uniform electric field created.

When a test charge is placed on the negative side of the plate, it will attract, and the force of attraction will be less. But when another test charge is placed closer to the positive side of the plate opposite to that of the other plate, the force of attraction would be more.

When the test charge is placed closer to the positive side of the charge, the repulsion is greater, and the force of attraction to the negative side of the plate is greater. So the force on a moving charge in an electric field depends on where the charge is situated and the distance.

Electric field is created only when the charges are at stationary. Therefore the force on that charge is determined based on the position of the test charge. Whether it is closer or far from the respective charges, it is placed.

How do you calculate the force of a moving charge

Force on moving charge in electric field is calculated using the formula is F = e E, here we consider the charge as electron and it is denoted by letter e. The electric field is denoted by letter E.

The force of the electron is nothing but the acceleration all over the mass of the electron in an electric field, and it is given as a = (e E) / m. This formula defines the electric field as the force by unit charge, E = F / q (e).

Now acceleration has been calculated, and the velocity goes like this, V_f² = V₀² + 2 a ∆ X. Where Vf is final velocity, and V0 is the initial velocity. The above formula is given in the assumption that the electron does not gain speed. This speed should not get too nearest to the light speed (3 X 10⁸ m/s), or else it would become a whole different scenario. Hence the speed of the charge must be below.

From the above picture, consider a negative test charge moving across electric fields. This charge has an initial velocity, and it will shoot up the electric field and not pass through it since two parallel plates have negative and positive charges on opposite sides. 

When an electron with a negative charge is placed between the plates, it gets deflected by the charges present in the vicinity. Since the uniform electric field is produced in the process, the charge travels faster with the initial velocity and is also perpendicular to the field.

The charge experiencing a force when deflected by the electric field it will give a projectile. The electron will displace from its original place (x) to a new position called y. This forms a projectile path.

Now there are possibilities for the charge to move out of the plates. When this happens, it makes an angle θ with a projectile path. Here we must know what (y) is and θ is. The deflection comes from the image, (y), and θ is the electron’s angle emerges out of the plates.

The electron placed between the plates experiences a force upwards because the side of the plate facing inward has a positive charge. Hence the electron will be attracted towards that side of the plate.

We need to calculate the force, acceleration, and velocity of the charge moving in the electric field. The force experienced by the moving charge in an electric field at point (y) is F_y = eE. Acceleration is a_y = (eE) / m.

The deflection (y) is formulated, and finally, we get the equation to calcite the force is as follows (y) = (eE x2) / 2my2. Then the angle at which the electron emerges out of the charged capacitor plates is as given, tan θ = (eEx) / mV₀² .

This is the basic formula we need to know before calculating the force on moving charges in the electric field. So, for now, we deal with simple techniques and so on.

Force on moving charge in electric field is the charge multiplied by the electric field or uniform electric field.

Force on a moving charge in a uniform electric field

We need to know that when a charge is in motion, it produces only a magnetic field. The charges which are not in motion produce electricity by default. Presence of an electric field causes magnetic field to be produced.

In a system, a point charge and a test charge is present. So the force exerted by the point charge on the test charge is called the electrostatic force. This is the force present on the moving charge in an electric field.

We can clearly understand how a force acts on a moving charge in an electric field using an example.

A charge travelling between the capacitor plates is attracted and repelled silmultaneously. When two plates are placed at a distance d the plates facing each other will have opposite charges.

So when a test charge is placed between, it will either get attracted or repelled depending on the magnitude it possesses.

Problems examples on Force On Moving Charge In Electric Field

From the above-shown diagram, we must determine the sign or charge of the particle moving in a projectile motion. We know that 1, 2 travel in one direction and 3 travel in another direction.

Positively charged plate is placed on top, and the negatively charged plate below. Both the plates are faced inwards. And the charges are inwards.

Now the charges 1 and 2 travel towards the positive side of the plate, and charge 3 travel towards the negative side of the plate.

Charges 1 and 2 are negatively charged, and charge 3 is positively charged. This is a very simple way to find the sign of the charge moving in the electric field experiencing a force.

We will have to determine the charge to mass ratio, whether high or low, based on the direction in which each of these charges travels.

Charge 3 will have a charge-to-mass ratio very high due to the deflection being high. Meaning, that charge three is deflected to a long position from its original position. Since the deflection is high, the charge to mass ratio is also high.

Consider two charged plates kept parallel to each other in a horizontal manner. Positively charged and negatively charged plates are placed top and bottom respectively. Length of the plate is l and the distance between the two plates is given by d

A charge mass m and charge +q are placed between the plates. This +q charge will be attracted to the lower plate. The electron has an initial velocity of V0. This velocity determines how far the charge will travel due to the presence of an electric field.

So now we need to find the minimum amount of initial velocity required to deflect more and just emerge out of the plates.

We know that the force is F_y = eE and acceleration is a_y= (qE) / m. Using this information, a tedious calculation is made, and finally, we get the equation for calculating the minimum initial velocity. And that will be V₀ = L {(qE / MD)}^1/2.

Problem on force on a moving charge in a uniform electric field

Let us consider a charge moving in an electric field. The charge is placed between the charged capacitors. A force acts on the charge while in its motion. The electric field acting on a point charge q= 2 NC is E= 7.91 X 105 N/C. What force does the electric field exert on the charge?

F= eE

F = 2 X 10-9C X 7.19 X 105

F= 0.180N

Now we have a clear understanding of force acting on a moving charge in an electric field.

*************************

Also Read:

• Is static electricity a contact force
• How to find normal force with coefficient of friction
• Gravitational force of earth
• Internal forces examples
• Force of friction examples
• Central force examples
• Coriolis force example 2
• Electrostatic force and distance
• Can normal force be at an angle
• What objects have magnetic force

External and internal forces are the two basic categories of the forces. External forces are further classified into contact forces and non-contact forces.

As the name itself says, an external force is a force that acts on a system by surrounding. The system needs force to accelerate or to change its kinetic energy, surrounding provides this external force to a system. Let’s discuss the External Forces Examples in detail.

External Forces Examples

• Frictional force
• Normal force
• Tension force
• Applied force
• Air resistance
• Buoyant force

Frictional force

When two moving bodies perform motion relative to each other, and the surfaces of these two bodies come in contact, friction occurs. This friction exerts some force on both the bodies and tries to stop their motion or helps them two accelerate.

Friction is a self-adjusting external force, so it adjusts according to the need for motion. Friction is an unbalanced force and is mainly divided into two types.

• Static friction is the friction between surfaces of two bodies when bodies are not moving relative to each other. Static friction mainly depends on the nature of the character and normal force. If the surface is smooth, the static friction is minimum, and rough static friction is maximum.
• Kinetic friction – It is the friction between two bodies when they are in motion. When the external force exceeds the value of static friction body starts to move, and the friction between surface and body decreases; this decreased friction is kinetic. The magnitude of kinetic friction is lesser than static friction.

Normal force  

The normal force is the force exerted by the flower on the body standing over that flower. The magnitude of the normal force is equal to the body’s weight, and direction is perpendicular to the surface over which the body is standing. Consider a block of mass M on a horizontal surface, the direction of the normal force is perpendicular to the surface, and the magnitude of the force acting on that block is,

Here, N- normal force on a block

          M- Mass of block 

          g – Acceleration due to gravity of Earth

Tension force

To produce tension in the string, we stretch a string, rope, or cable by two ends. Tension plays a crucial role in pulling heavyweight or hanging the weight at a certain height. Tension is a contact force that transmits through the rope or cable and pulls or holds the object.

When we pull a certain object using rope or cable, we can change the direction of applied force using a pulley, and in this system, the tension in both sides of the string is the same. If a mass is suspended from a ceiling using two ropes and in a stable condition, then in this cause, the tension in the string can be calculated using Lami’s theorem; otherwise, Newton’s second law of motion is used to calculate the tension.

Applied force

It is an external force directly applied to a body by a person or another body. This force is responsible for the acceleration of a body, and this force is non-conservative. Consider a wooden block of mass M on a horizontal surface. A block needs some external force to move from its position, so when we apply force on a block, it starts to accelerate in the direction of the force.

In daily life, we use this force mainly to push or pull things from their position. We can gain a mechanical advantage by using simple machines like lever and axle wheel.

Where, m- mass of an object

a- acceleration of the object

Air resistance

What happens when we drop a feather from a certain height? Why it falls slower than a stone of the same weight? Why can’t it fall straight on the ground? The answer to all of these questions is air resistance or drag. Whenever an object falls from a certain height or moves with a certain velocity, the air applies a resistive force on an object in the opposite direction of motion. his resistive force is called air resistance

Air resistance is also an external force, so it is a non-conservative and dissipative force in nature. The skyscrapers like Burj Khalifa also face air resistance, so to avoid this resistance, structures are built so that the air resistance should be minimum.

To calculate the air resistance following formulae is used,

Where c – force constant

V – velocity of an object

Buoyant force  

Have you ever think why we feel lighter in water than on the ground? It happens because water exerts pressure on the body’s surface. As we go deeper in water, the pressure starts to rise. The pressure on the lower part of the submerged body is higher than the upper part, and because of this pressure difference, the body gets pushed towards the water’s surface.

the expression for buoyant force is,

Where ρ- density of fluid

g- acceleration due to gravity

V_f-volume of displaced fluid

FAQ’s

What is internal force?

Forces are divided into internal and external forces on the basis of their interaction with system

 The force that acts on the system internally and produces a change in the system or opposes the change in the system by an external force is called internal force. internal forces are produced inside the system, and they can not produce an external change in a system such as acceleration of system or change in kinetic energy of the system.

Why external forces are non-conservative?

The reason behind external forces, also called non-conservative forces, is as follow

External forces depend on the path by which motion of a system occurs, so they do not have potential energy. Similarly, external forces are dissipative, which means, over the period, the system loses energy, so the system’s energy is not conserved. Hence they are also called non-conservative forces.

Is gravity an external force?

The internal and external force is depends upon the system under the study

Gravitational force is the attractive force between two particles of a system. In gravitational force, we study the interaction between two or more particles. Also, the total energy gets conserved in the gravitational force. Hence the gravity is an internal force.

Also Read:

• How to find normal force on a horizontal surface
• Muscular force examples
• Is applied force a contact force
• Is muscular force a contact force
• What is magnitude of force
• How to calculate force of gravity
• Exert force example
• Is friction a conservative force
• Electrostatic force and distance
• What objects have magnetic force

Internal Force resists the influence of External Force on an object.

Internal Force is a contact force responsible for keeping an object intact when the loads due to External Force act on it. It can cause acceleration in different parts without disturbing its equilibrium because it acts from within the object.

No force is inherently internal or external; it all depends on how the system and the forces acting on it are considered. In any system with an action-reaction couple, the applied force is usually termed the internal force. Let us discuss a list of Internal Forces examples below to understand the physics behind them.

Trembling of a tree owing to wind

When the wind blows on a tree, it causes it to swing.

This force of the wind is influenced by external factors and can tremble the tree excessively at its position, thereby uprooting it from the ground. On the other hand, the internal force is the force that helps the tree stay in place and prevents it from falling.

Bending of a scale due to applied pressure

Muscular weight applied on the edges of a measuring scale can cause it to stretch.

A significant amount of both tension and compression is present in the measuring scale. The external force is the muscle force acting on the scale. This force has a large enough magnitude to bend but not shatter the scale. This is because it is supported by an internal force that prevents it from breaking.

Pushing a bus

Pushing a bus while sitting inside it and from outside results in two different situations.

Pushing a bus while sitting inside it won’t cause any movement in it. Whereas, trying it externally after exiting from the bus can make it move ahead because the external pushing by the passengers introduces an outward force on the bus.

The passengers when seated inside the bus, make a cumulative system and hence any force applied during this time does not cause any movement in the vehicle. Hence this is an internal force that exists within a system that prevents it from moving and counters the load applied by an external force.

The action of a spring

When a force is applied to the spring to extend it, the spring moves.

The force acting on the spring is external whereas the internal force compresses the spring to gain back its original shape. The internal force is diametrically opposed to the exterior force, and it opposes the motion and any change in form.

Pushing of a chair

Pushing a chair while sitting on it and standing on the ground gives rise to two different scenarios that can classify internal and external forces, respectively.

A chair moves in the direction of the applied force, when pushed by a person while standing in its proximity. At the same time, no movement is witnessed when the chair is pushed while sitting on it. Both the situations witness same amount of force applied in the same direction. The sole distinction is in the method of evaluation.

The former case involves application of an external force and hence movement in the chair is seen. In the second situation, however, the chair does not move since the person sitting in it has become a component of the system. As a result, the force acting here is referred to as an internal force.

Compression of a sponge

Compression acting on a sponge body is another example of internal force.

When a person rubs his hand against a sponge’s surface, the sponge’s shape changes. Because the person’s force acts within the system, the compression force is an internal force. This internal compression force opposes motion that aids the sponge in regaining its previous shape.

Tension in a rubber band

The stretching of a rubber band causes tension in it which is an internal force.

When a rubber band is tugged or stretched, the tension force is created. The original shape of the object is restored when the pull force is lifted. The force is said to be internal because the interaction occurs within the object or system. On the other hand, the external force is the force used to stretch the band and generate motion to change its shape.

Wringing out a washcloth

The twisting force of torsion is used to wring out a damp washcloth.

The washcloth is twisted in opposite directions from its either ends to squeeze the water out of it. Torsion is a force that twists or turns and originates from within the object. Hence it is an internal force.

The collision between hockey pucks

Let us consider two hockey pucks sliding across a frictionless surface and colliding with each other at t=0; to keep the problem simple enough for evaluation, we ignore air resistance.

There are three fundamental forces working on the bodies- the force acting mutually perpendicular to the ice and the hockey pucks, gravity, and the friction cause due to collisions between the pucks. Our system takes in account the two pucks only because our subject constitutes of the motion between the pucks only.

Hence the frictional force between the pucks acts as internal force because conservation of momentum is applicable in this case. When the rest of the Earth is included in our system, gravity and normal forces become internal forces as well.

Kinematics of muscles and tendons in the human body

Muscles and tendons are the structures that produce the forces that cause our kinematic state to change.

Muscle activity generates internal forces that induce motions of the extremities and other body components. Still, it is impossible to change the movement of the human body’s center of gravity without the presence of external forces. Only when the human body comes into contact with another thing can it change its motion.

Internal force research can be used to characterize particular body component motions and the nature and causes of injuries.

Earthquakes and Volcanic Eruptions

The surface of the Earth, where humans live, is characterized by an infinite variety of morphological shapes.

The narrow trenches swipe down the bottommost surface of the ocean while the enormous abyssal plains steep it up to the seamounts and the ridges. Whereas, mountain belts to volcanic chains, and hilly areas to flat lowlands range over the periphery of the continents. The generation of heat in the Earth’s interior, which causes internal or endogenous forces in geology.

Internal forces are responsible for all vertical and horizontal movements of the Earth’s crust and some extreme calamities like earthquakes and volcanic eruptions.

Frequently Asked Questions (FAQs)

Q: What are internal forces caused by?

A: One part of an object operating on other sections of it causes internal forces.

Internal force is a collection of contact forces that does not cause an object’s balance to be disturbed. The internal force vector’s elements cancel out and hence do not contribute to the final force applied to the thing.

Q: Are internal forces always balanced?

A: Internal forces are commonly referred to as conservative forces because they do not modify an object’s overall mechanical energy; hence they are always balanced in the case of non-deformable rigid bodies.

Q: What are the four basic types of internal force?

A:  The four basic types of internal force are:

• Compression: The material gets squeezed under this force of ‘push’ nature.
• Tension: The material flexes under this force of ‘pull’ nature.
• Torsion: The material experiences a twisting force, i.e., turning force.
• Bending: The material loses its straightness and bends.

Also Read:

• Muscular force examples
• Gravitational force of moon
• Force on moving charge in electric field
• Newtons law of gravitational force
• Is support force a contact force
• Negative electrostatic force
• Displacement and force
• How to find normal force between two blocks
• Does the direction of magnetic force change
• Is magnetic field and magnetic force same

In a rope, cable or string tension is created when we pull them from both ends in opposite direction. Here we are going to discuss the nature of tension force, is tension a conservative force or non-conservative?

Tension is a non conservative force but it is not dissipative in nature, which means there is no energy loss of energy. As it is a non conservative force tension force does not have any potential energy associate with it, similarly the work done by the tension is always zero.

Tension force

Tension is a contact force, and it transmits through the rope or cable, which we are using to pull or hold the object, also it is a self adjustable force it adjusts according to the need. When the limit of tension force is exceeds the rope gets break tension becomes zero. Tension force does not have any special formula to calculate its magnitude, so we use Newton’s second law to calculate the tension in a rope or cable.

Consider a mass M is hanging from roof by a inextensible string, to calculate the tension in a string we use the Newtons second law. The block is in stable condition, which means acceleration of block is zero. So the equation of the Newton’s second law will be,

Here T- tension in the string

This is the tension in the string due to mass M.

Now let’s see what conservative and non conservative forces are,

Conservative force –

The force which are depends on the initial and final displacement of the object and not depend upon the path of motion is called conservative force, for example gravitational force, electrostatic force, etc. In conservative force work done is independent of path and similarly potential energy is associated with conservative forces. Total energy under conservative force remains constant.

Non-conservative force –

 Total energy is not remains constant under the influence of non-conservative force forces. In the non- conservative forces work done is depends upon the path by which motion occurs. Friction force, tension, force over a wooden block, these are some examples of the non conservative forces.

FAQ’s

Why non-conservative forces have no associated potential energy?

Potential energy is a stored energy that can be reusable at any time.

 When a system do some work against a force that work gets stored in system in the form of change of shape, change of position or configuration. The non-conservative forces are path dependent quantities and not depend upon the initial and final condition of system, that’s the reason potential energy, is not associated with non-conservative forces

Why tension is not dissipative in nature?

Dissipative force means the force in which energy gets lost.

The non-conservative forces are dissipative in nature because working against this forces system’s energy gets lost, for example in friction force energy gets lost in the form of heat. Tension is exception to this because in there is no loss of any energy in the tension force.

 Is conservative forces are path dependent or independent of path of a motion?

Mostly conservative functions are path independent, they depend on initial and final position of system.

The conservative forces are independent of path of a system. They are mostly depend on the initial and final position of a system.

Why the work done by tension is always zero?

The reason for zero work done is as follows,

Tension acts opposite to the direction of motion and as the direction of force and motion are opposite there is no actual displacement when we apply tension. Work done is the product of force applied on a system and the displacement of the system. As the displacement due to the tension is zero the work done by the tension is also zero.

Also Read:

• Gravitational force 2
• What increases the force of a magnetic field
• Internal forces examples
• Forces in static equilibrium
• Electrostatic force examples
• Is static electricity a contact force
• Is tension a contact force
• Natural frequency and forced vibrations
• Negative electrostatic force
• Force on moving charge in electric field

Forced oscillations examples are seen or is performed in our daily life. There are innumerous examples in our real-life where the force is applied for any oscillation to be performed. Here are a few forced oscillations examples which can be seen or is performed near us in our day to day life:

Parents pushing their child on a swing

In a playground or park, it is a normal view that can be seen where there is a swing. Parents or elders come with their children to let them enjoy the ride on a swing. Here, they continuously push the swing at short intervals for the swing to oscillate.

The pushing of the swing seems to be normal, but the science behind it is too complex. If a person pushes the swing once, it will stop after a certain no. of oscillations where the speed decreases simultaneously. This is caused by the interruption of air resistance and other forces applied by nature. While, continuous external force at regular intervals increases the energy lost by damping.

A potter rotating a potter’s wheel

If you have visited a potter, you might be familiar with the big wheel they keep at their home for working with it. They used that wheel known as potter’s wheel to make clay pots using the potter wheel throwing method.

In this method, they need to continuously rotate the wheel at regular short intervals for the formation of clay pots and vessels. This ancient method which is still used today, is a perfect example of forced oscillation is being persistingly used since past.

Read more about: What is High Viscosity: Critical Facts

Applying force for movement of a pendulum

A pendulum is an object which is freely suspended and allowed to move. This pendulum comes to rest after a certain time completing its oscillation. To continue its to and fro movements, a certain external force is needed to be applied at regular intervals before its maximum displacement reaches to negative.

Boy pedaling his bicycle

A boy with a bicycle uses his legs to move his bicycle. This external force applied by him for pedaling helps him to rotate the wheel connected to the bicycle, which causes the movement of the bicycle.

An RLC Circuit

An RLC circuit consists of main parts i.e., resistor, inductor and capacitor. Here if the charged capacitor is discharged, the current then flows to the inductor. Thereafter, a magnetic field is created by charged inductor, which collapses the current being sent back to the capacitor.

Read more about: Low Viscosity Fluids: Exhaustive Examples with Explanation

What is Forced Oscillation?

The oscillation caused to a body by the impact of any external force is called Forced Oscillation.

Forced oscillation can be defined as an oscillation in a boy or a system occurring due to a periodic force acting on or driving that oscillating body that is external to that oscillating system.

Suppose, in a playground, a boy is sitting on a swing. Another boy stood behind the swing and pushed the swing once, and the swing starts to show a to and fro movement.

In this case, the swing started to oscillate fastly, once pushed by another boy. But later, the speed of swing will start to decrease by the obstruction of air resistance, gravitational force, and other forces acting on it by nature. This decrease in the speed of the swing by the obstructions will eventually lead the swing to stop.

Now, let us take the same situation of a boy sitting on a swing in a playground being pushed by another boy standing behind the swing the first boy was sitting on with a slight change in the action of the second boy.

Let the second boy who is standing behind the swing pushes the swing more than once continually at a regular interval before the maximum negative displacement is reached by the swing.

You will observe that if there is continuous external force is applied every time to the swing, the swing will move continuously despite the obstructions caused by nature until the externally applied force is not stopped by the second boy. This is because the energy lost while the damping is recovered by regular pushes.

You will also observe that if the less external force is applied continually than the previous push, then also, the speed of the swing will decline but upto some extent where the swing will not stop the movement of its oscillation.

While, if the external force which is applied to the swing is much more than the force applied everytime, then it may happen that the boy may be out of synch with the natural frequency of the swing. This can even cause a drastic change affecting both the boy and the swing to collapse.

From above instance we can conclude the following statement about Forced Oscillation:

Forced Oscillation is a type of oscillation where an external force is continuously applied at regular intervals to keep the system or body in oscillation.

Read more about: High Viscosity Liquids: Exhaustive Examples With Explanation

Also Read:

• How to find tension force in a pulley
• Is tension a contact force
• Spring force vs spring constant
• What increases the force of a magnetic field
• Newtons law of gravitational force
• Is net force a vector
• Exert force example
• Is tension a conservative force
• Is force a vector quantity
• Central force examples

       The electric force is the interaction between any two charged bodies. It is the reason behind particular phenomenon occurring around the world.

The electric charge experiences an electric power which is a push or a pull. Here in this article, we will see a few examples of electric force to understand the concept better.

Electric Circuit

               In an electric circuit, the flow of charges conducts electric current, and the force existing between these charges is known as force of electricity.

               It is universal that electric force is a form of non-contact force. Electric change is nothing but the movements of charge in a body. There are basically two types of electric charges, positive and negative, respectively.

                 In an electric circuit, an electric current is present, and this electric current is the flow of these charges in their respective directions based on the magnitude of the charges.

                 As we know, like charges repel, and unlike charges attract, the two positive or negative charges repel, one positive or negative and one negative or positive charge attracts.

The charge present in a bulb

In a bulb, the current always flows from high potential to low potential. The high potential is the positive terminal, and the low potential is the negative terminal.

                  According to the Law of Conservation of energy, energy is neither destroyed nor created but can be transformed from one form to another. The electric bulb is one such object that works under this law.

                  In an electric bulb, the electric energy is converted as light energy. There arises a force during this conduction of charges. The two terminals of the bulb are conducted to the Tungsten filament.

                When an electric current is passed between the terminals, the thin Tungsten filament is heated up by the electrons that flow in such a way that the bulb begins to glow. This process happens at a fast rate.

                The Argon gas present inside the bulb prevents the thin filament from breaking and overheating. The charges in a bulb move in such a way creating electric force in them.

The electric charges present in the bulb move so as to conduct electric current and also electric force.

Standing Hair

The common phenomenon of standing hair is due to the electrostatic force. The standing hair is normally an experiment to prove the presence of electric force and due to the electric current.  This experiment was conducted by Van de Graff generator.  

                Van de Graff generator picks up static electricity of high voltage by transferring charges using a conveyor belt that is synthetic and this goes on continuously. These charges are transferred and then accumulate in a hollow metal globe. Positive charges, when transferred, get repelled to each other, making one’s hair stand.

Lightning

            Lightning occurs during a powerful electrical charge-discharge. Thunderstorms are caused by small electrically charged particles when water molecules are heated and cooled, moving up and down against each other.

             In clouds, there goes on a process where the charges take two separate parts and arranges themselves accordingly, where one part will be negative and the other will be positive. So based on this separation, the particles on the ground gets arranged oppositely compared to the lower part of the ground.

              Imbalance occurs when such a process happens so electric current is passed between the charges, and they flow in the direction of fewer particles of the same charge. This very occurrence results in a lightning bolt. This lightning sometimes carries positive or negative charges.

              In the beginning, the lightning becomes invisible, but when the electric discharge is so powerful, their lightning arc occurs, which then becomes visible. Lightning sometimes occurs in a different color, and this is due to atmospheric humidity, temperature, and air pollution too.

                Since lightning is so powerful, there are several ways to extract electricity from it. But these are only theoretical ideas and require massive equipment to conduct this experiment.

Current Electricity

              Whenever there is an electric current, there will be an electric field and then follows the electric force.

               In a conducting wire, there is an electric current because of the electric field presence, and this electric field exerts a push to the electrons to move along.

               Different charges attract each other, and the force existing between charged bodies is known as an electric force. The interaction between the charges that are electrically charged is called electric current. The direction of the force that exerts on a positive test charge affects the direction of the electric field.

                The flow of charged particles in any conductive body produces an electric current when high voltage is provided. The electric force is nothing but the force existing between the charged bodies.

Glass rod and Silk

In this experiment, a glass rod is rubbed with a cloth; the charged particles are transferred from the cloth to the glass rod.

                  Simply when the glass is brought near another one, it does not move. When the rubbed glass is brought again, the other rod deflects in the direction of the charged particles.

                   For example, when the glass is positively charged, and another one has a charge of the same polarity, they repel, but they attract each other if they have different charges. This occurs because of the electric force in action.

Balloon and paper cuts

                  Taking two balloons and bringing them close to paper cuts does not carry any difference or any effect. Now when the balloons are rubbed together, charges get transferred onto each other. The main reason for such occurrence is that the charged bodies have some force existing between them.

                 When the balloons are rubbed against each other, electrons get transferred from one balloon to another, now the charges are equally placed, but there is also an imbalance.

                  Since the balloons are charged and brought to a paper cut, it slowly sticks the balloon. The electric force is ne main reason for this experiment to be proved.

********************************

Also Read:

• How to find normal force with coefficient of friction
• Gravitational force examples
• Force on moving charge in magnetic field
• Electrostatic force examples
• How to find tension force in a pulley
• Is air resistance a force
• Atomic force microscopy
• Electrostatic force and charge
• Is net force a vector
• How to calculate force of gravity