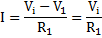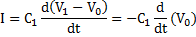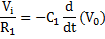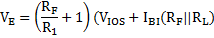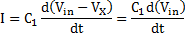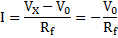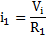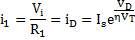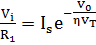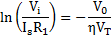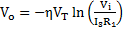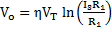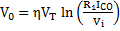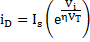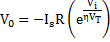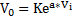In this article we will study about the Schmitt trigger Comparator and Oscillator circuitry with different related parameters in detail. As we have seen till now that an op-amp is used in various fields of applications and being such a versatile device its importance as a part of analog circuits is immense. One of the most convenient applications of the op-amp is as a multivibrator circuit. We will be studying in detail about types and working of multivibrator circuit constructed using op-amps (op-amp multivibrators) and other passive devices such as capacitors, diodes, resistors etc.
Contents
- Introduction of Multivibrators
- Positive feedback usage in multivibrator
- What is Schmitt trigger ?
- Schmitt trigger comparator closed-loop circuit or bistable multivibrator
- Voltage transfer characteristics of Bistable multivibrator
- Astable multivibrator or Schmitt trigger oscillator
- Oscillator’s duty cycle
Introduction of Multivibrator and Schmitt trigger Circuitry
Multivibrator circuits are sequential logic circuits and are of many types depending on how they are created. Some multivibrators can be made using transistors and logic gates, whereas there are even dedicated chips available as multivibrators such as NE555 timer. The op-amp multivibrator circuit has a few advantages over other multivibrator circuits as they require much fewer components for their working, less biasing, and produces better symmetrical rectangular wave signals using comparatively fewer components.
Types of Multivibrators
There are mainly three types of multivibrator circuits present:
- Astable multivibrator,
- Monostable multivibrator
- Bistable multivibrator.
The monostable multivibrator has single stable state, whereas the number of stable-states a bistable multivibrator has- is 2.
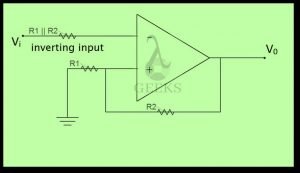
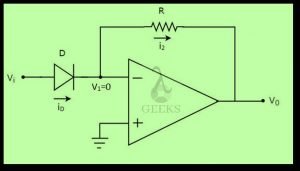
As we have learnt in the previous section about op-amp as a comparator, in the open-loop configuration the comparator can switch in an out of control manner between the positive saturation supply rail voltage and negative saturation supply rail voltage when an input voltage near to that of the reference voltage is applied. Hence, to have control on this uncontrollable switching between the two states, the op-amp is used in a feedback configuration (closed-loop circuit) which is particularly known as closed-loop Schmitt trigger circuit or bistable multivibrator.
Positive feedback usage in multivibrator and hysteresis effect
Till now, we have learnt about the negative feedback configuration in op-amps in the previous sections. There is also another type of feedback configuration known as positive feedback, which is also used for specific applications. In positive feedback configuration, the output voltage is fed back (connected) to the non-inverting (positive) input terminal unlike the negative feedback, where the output voltage was connected to the inverting (negative) input terminal.
An op-amp operated in a positive feedback configuration tends to stay in that particular output state in which it is present, i.e. either the saturated positive or saturated negative state. Technically, this latching behaviour in one of the two states is known as hysteresis.
If the input applied signal in the comparator consists of some additional harmonics or spikes (noise), then the output of the comparator might switch to the two saturated states unexpectedly and uncontrollably. In this case, we won’t get a regular symmetrical square wave output of the applied input sinusoidal waveform.
But if we add some positive feedback to the comparator input signal, i.e. use the comparator in a positive feedback configuration; we will be introducing a latching behaviour in the states, what we technically call as hysteresis into the output. Until and unless there is a major change in the magnitude of the input AC (sinusoidal) voltage signal, the hysteresis effect will continue to make the output of the circuit remain in its current state.
What is Schmitt trigger ?
The Schmitt trigger or bi-stable multi-vibrator operates in positive feedback configuration with a loop-gain greater than unity to perform as a bi-stable mode. Voltage V+ can be.
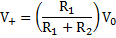
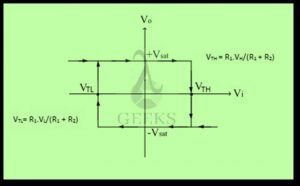
The above figure represents the output voltage versus the input voltage curve (which is also known as the voltage transfer characteristics), particularly showing the hysteresis effect. The transfer characteristic curve has two specific regions, the curve as the input voltage increases and the part of the curve in which the input voltage decreases. The voltage V+ does not have a constant value, but instead, it is a function of the output voltage V0.
Voltage transfer characteristics
In the voltage transfer characteristics, Vo = VH, or in high state. Then,
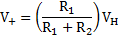
Higher Cross-over voltage VTH
If signal is less than that of V+, the output stays at its high state. The cross-over voltage VTH occurs when Vi = V+ and expressed as follows:

When Vi > VTH, the voltage at the inverting terminal is more than at the non-inverting terminal. Voltage V+ then turn out to be
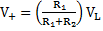
Lower Cross-over voltage VTL
Since VL < VH the input voltage Vi is still more than V+, and the output rests in its low state as Vi carry on to increase; If Vi decreases, as long as the input voltage Vi is larger than V+, the output remains at saturation state. The cross-over voltage here and now occurs when Vi = V+ and this VTL expressed as
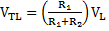
As Vi continues to decrease, it remains less than V+; therefore, V0 remains in its high state. We can observe this transfer characteristic in the above figure. A hysteresis effect is shown in the net transfer characteristic diagram.
What is Schmitt trigger oscillator ?
Astable multivibrator or Schmitt trigger oscillator
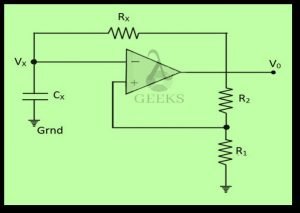
Astable multivibrator accomplished by fixing an RC network to the Schmitt trigger circuit in –ve feedback. As we will advance through the section, we will see that the circuit has no stable states and therefore, it also known as the astable multivibrator circuit.
As noticed in the figure, an RC network is set in the negative feedback path, and the inverting input terminal is connected to the ground through the capacitor while the non-inverting terminal is connected to the junction between the resistors R1 and R2 as shown in the figure.
At first, R1 and R2 is to be equal to R, and assume the output switches symmetrically about zero volts, with the high saturated output represented by VH = VP and low saturated output indicated by VL = -VP. If V0 is low, or V0 = -VP, then V+ = -(1/2)VP.
When Vx drops just slightly below V+, the output switches to high so that V0 = +VP and V+ = +(1/2)VP. The equation for the voltage across the capacitor in an RC network can be expressed as:
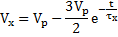
Where τx is the time constant which can be defined asτx= RxCx. The voltage Vx increases towards a final voltage VP in an exponential manner with respect to time. However, when Vx turn out to be slightly greater than V+ = +(1/2)VP, the output shifts to its low state of V0 = -VP and Vx = -(1/2)VP. The RxCx network gets triggered by a negative sharp transition of the voltages, and hence, the capacitor Cx start discharging, and the voltage Vx decreasing towards value of –VP. We can therefore express Vx as
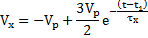
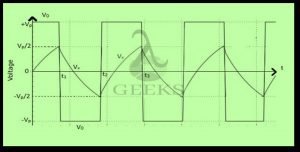
Where t1 refers to the time instant when the output of the circuit switches to its low state. The capacitor discharge exponentially V+ = -(1/2)VP, the output again shifts to high. The process repeats itself continuously over time, which means a square-wave output signal is produced by the oscillations of this positive feedback circuit. The figure below shows the output voltage V0 and the capacitor voltage Vx with respect to time.
Time t1 can be found by substituting t=t1 and Vx = VP/2 in the general equation for the voltage across the capacitor.
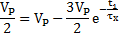
From the above equation when we solve for t1, we get
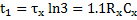
For time t2 (as observed in the above figure), we approach in a similar way, and, from a similar analysis using the above equation, it is evident that the difference between t2 and t1 is also 1.1RxCx. From this, we can infer that the time period of oscillation T can be defined as T = 2.2 RxCx
And the frequency thus can be expressed as
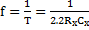
Duty cycle of Oscillator
The percentage of time the output voltage (V0) of the multi-vibrator is in its high state is particularly termed as the duty cycle of the oscillator.
The oscillator’s duty cycle is
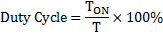
As observed in the figure, depicting output voltage and capacitor voltage versus time, the duty cycle is 50%.
For more Electronics related article click here