Rabiya Khalid - lambdageeks.com

What Is Amplitude Of Motion: How to Calculate It

January 21, 2024November 18, 2021 by Rabiya Khalid

Simple harmonic motion is a form of periodic motion in which an object or particle moves about its central position. Let us know what is amplitude of motion.

In SHM, when a body moves about a fixed point, it covers displacement on either side of the point. This maximum displacement covered by a particle or object is termed the amplitude of motion. There is a possibility of it being negative, which only shows the displacement in the opposite direction.

We all have seen or know that it starts vibrating for a few seconds on striking the guitar string. It first moves from its equilibrium position to one side and then goes to the other side from passing through to the equilibrium position. Now, this whole to and fro motion of the string is the periodic motion.

Here one more thing arises when the string starts vibrating, a restoring force emerges, which acts directly proportional to the particle’s displacement. Hence this is a simple example of simple harmonic motion.

In this example, the displacement of the string on either side of the central position is its amplitude. Let us understand it in a simple method. When we march past, our hands swing front and back. Now the extent to which you lift your hand will be its amplitude.

guitar 1473400 1280 — What is amplitude of motion
Image Credit: Pixabay

We know that the SHM is a sinusoidal wave equation. Hence the motion of a particle is represented as the wave diagram.

In this figure, we can see that the particle is making equal maximum displacement on either side. Therefore the distance XY is the amplitude of the motion. The symbol to symbolize amplitude is A, and since it is a measure of displacement, its standard unit is meter (m). There can be another unit as well, like centimeters.

How to calculate the amplitude of motion

We have understood what is amplitude of motion now; the next question that arises is how to calculate the amplitude of motion. The simple harmonic motion is a sinusoidal wave function; therefore, the SHM equation can be represented as a function of sine or cosine.

x = A sin (ωt + ϕ) or x = A cos (ωt + ϕ)

Here,

x is the displacement of the wave

A is the amplitude of motion

ω is the angular frequency

t is the period

ϕ is the phase angle

From the above equation, we can calculate the amplitude of the motion.

Suppose we are given the SHM equation as x = 2sin(4t). Now, comparing the equation with sinusoidal wave equation x = A sin (ωt + ϕ), we get amplitude as 2 metres.

Screenshot 2021 11 17 221844 — What is amplitude of motion

For the given diagram, we can easily calculate the amplitude. From the figure, the amplitude is 5 m.

Frequently Asked Question (FAQs)

What is simple harmonic motion?

In physics, motion can be varied, like simple harmonic, wave, and circular motion.

The simple harmonic motion is the to and fro movement of a particle or object. In this motion, the restoring force acts indirectly proportional to the amplitude. Example: musical instruments, bungee jumping etc.

Is SHM the same as a periodic motion?

Periodic motion is the one in which a body repeats its motion in regular intervals.

Simple harmonic motion is a particular case of periodic motion in which, on movement, a restoring force emerges, which increases or decreases with the amplitude of the motion.

What is amplitude of motion?

To define a simple harmonic motion, we use some basic physics concepts. One of them is amplitude.

Amplitude is the maximum displacement that a body or particles complete about its central point. Suppose a bouncing ball reaches a maximum height of 50 cm, then the amplitude of the ball becomes 50 cm.

Give an example of the amplitude of motion.

The amplitude of motion is the maximum displacement of a moving body.

In the above figure, we can see that the pendulum displaces on either side till point A and B. Therefore, the distance OA and OB become the amplitude of the moving pendulum.

How to calculate the amplitude of motion?

The simple harmonic motion is a sinusoidal wave function. Its equation can be represented as s sine or cosine function.

The SHM equation is represented as:

x = A sin (ωt + ϕ) or x = A cos (ωt + ϕ)

Here,

x is the displacement of the wave

A is the amplitude of motion

ω is the angular frequency

t is the period

ϕ is the phase angle

The equation is used to calculate the amplitude of the motion.

On what factors does amplitude depend?

Amplitude depends only on the energy of the moving body.

Amplitude is directly proportional to the square root if dissipated energy. It further does not depend on any other factor of SHM like frequency or time period.

How does amplitude affect the motion?

The restoring force that emerges is directly varied to the amplitude of motion.

The rise in amplitude leads to an increase in the force, which further increases the acceleration. The amplitude does not have any effect on the frequency and angular frequency. Therefore amplitude does not affect the motion.

What is the symbol and unit of the amplitude of motion?

The amplitude of a moving particle is the distance between the central and extreme points.

The amplitude of the motion is denoted by the symbol A since it is the measure of displacement, therefore its unit meters. It gives the idea about the extent the body can move and gain the highest position.

Also Read:

How Can A Physical Change Occur: Detailed Analysis

January 21, 2024November 9, 2021 by Rabiya Khalid

The changes that can reverse and, in the same cases, remain irreversible are generally physical changes. Let us see how can a physical change occur.

The physical change occurs when the changes take place in the physical properties of the substance or the object. The changes in shape, size, or state can be brought in different ways, either by the transfer of energy, heat, or physical means.

The physical changes can occur by the following means:

Cutting/Breaking
Melting
Freezing
B oiling
Dissolving
Mixing

Cutting/Breaking

pencil 1203982 1280 — Image Credit: Pixabay

When we cut, break, or tear something, the size or shape gets deformed. Due to this type of alternation, a physical change occurs. For instance, when we cut fabric to make a dress, it is a physical change. The fabric and the dress are made of the same chemical composition, secondly on breaking a pencil or a crayon, its shape and size change. The pieces still remain the part of a pencil. Hence on breaking or cutting, a physical change occurs that brings alterations in the shape and size of the object.

Melting

Melting is another way by which a physical change can occur on melting the phase or, say, the state of the substance changes. When the ice cream starts melting, it changes into a liquid state, but the taste and all the chemical characters continue to stay the same as that of the solid or semi-solid ice cream. On melting, we receive a liquid version of ice cream,m. Now, this process is reversible, and we can gain the original state of the ice cream back. So this proves that on melting, the physical change takes place.

Freezing

ezgif 7 d54725365f50 — Image Credit: Pixabay

For making jelly, the mixture has to be cooled and frozen. When we do so, the liquid state of jelly gets converted into a solid or semi-solid state. During this process, only the state changes, and all the internal composition remains the same. It does not involve the breaking of bonds or the formation of new bonds. Hence this change can be inferred as the physical change. We know that it is only a temporary change as the process can be reversed at high temperature. Through this example, we understand that freezing is another process that causes a physical change to occur.

Boiling

Boiling can also bring physical changes to occur. It causes the phase change of a substance. When we boil water at its boiling point, the water changes into vapor form. Now, water is liquid, and vapor is gaseous. So changes occur in the state of water, but the chemical formulas of both states are the same. The vapor can be reversed back into the water by the process of condensation. So on boiling, the physical change occurs.

Dissolving

How can a physical change occur — Image Credit: Pixabay

Dissolving is the process in which we add solute particles into a solvent and make a solution. When we dissolve two substances together, there is no release or intake of energy, and hence internal energy remains the same. The solvent molecules get further apart, and solute molecules get inserted. It does not lead to the emergence of any new substance, and therefore the whole process is the physical change. The example of dissolving is salt and water. On evaporation, the salt can be generated back. Hence on dissolving, the physical change occurs.

Mixing

Mixing also causes a physical change to occur. When we mix different colors, we obtain a new color. Only a different color is generated; no new substance is formed. Therefore mixing also causes physical change. In some cases, the change is reversible, and in others, it is irreversible.

Frequently Asked Questions (FAQs)

Is freezing a chemical or physical change?

The everyday changes happening around us can be categorized as physical change or chemical change.

The process of freezing is a physical change. The reasons are simple as it does not lead to the formation of any new substance. The change is caused only in the phase. Also, the substance can be brought back to its initial state. Hence freezing is a physical change.

How can a physical change occur?

The numerous physical changes occur all around us in different forms.

The physical change occurs through physical means. The change in physical characteristics of objects like length, structure, or state is known to be a physical change.

Which process leads to physical changes?

The changes in physical characteristics of a substance are said to be physical changes.

The melting, freezing, cutting, dissolving, and other such types of physical processes lead to the occurrence of physical change. All these processes can either be reversed or stay the same. They cause changes in physical properties.

Give five examples of physical change.

Physical change is the transformation caused by the physical properties of the substance.

The five examples of physical change are melting ice, cutting trees into logs, tearing paper, dissolving sugar into water, and folding clothes. All these changes involve alterations in the size, shape, and phase of the object. They are either reversible or irreversible.

Is the growth of plants a physical change or a chemical change?

The whole process of the growing tree is both a physical and a chemical change example.

The growth leads to an increase in the height and width of the tree; therefore, it is considered a physical change. At the same time, growth involves the photosynthesis process; therefore, it is also a chemical change. So a growing tree is both a chemical and physical change example.

Also Read:

When Does A Physical Change Occur: Detailed Analysis

January 20, 2024November 8, 2021 by Rabiya Khalid

The changes happening around us are either chemical or physical changes. Let’s have knowledge about when does a physical change occur.

Physical changes occur when the substance undergoes a transition in the physical properties. Any change in the state, shape, color, or size of the object is said to be a physical change. They are generally known as temporary changes. The physical change can either be reversible or irreversible.

A physical change arises due to changing physical properties, i.e., size, shape or state, etc. Generally, physical change is caused by applying force or energy to the object. During a physical change, the total internal energy before and after the reaction or change remains the same. This means that the bonds of the object or substance remain intact. It does not break to form a new substance.

Let us understand a common example of physical change that is the melting of butter or vice versa. For melting butter, energy is required. Now this energy should be sufficient enough to change the state of the butter and does not break the bonds. When the butter acquires this energy, its molecules gain energy and come in rapid motion. Due to this, they only get apart and change into a liquid state. And hence physical change occurs.

buttered 18641 1280 — Image Credit: https://pixabay.com/photos/buttered-toast-food-bread-18641/

This change can be reversed, and butter can regain its original state on freezing, thus leading to phase change. Now physical change can also occur by changes in size, shape, odor, color, temperature, or pressure. Now when you break a pencil into two halves, its shape and size both get changed, and hence physical change has occurred.

Image Credit: Andy Schmitz, Sodium chloride dissolution, CC BY 3.0

Let’s take another case of sugar dissolving into the water. Now, this is a common example of reversible physical change. Many a time, it is confused to be a chemical change. For this, let us see how a physical change occurs. On dissolving sugar into water, no new substance is formed with no chemical reaction. During the process, the thing that happens is the change in form. The identity of both the solute and solvent remains the same. Here the water that is our solvent gets its molecules further apart, and sugar molecules fill that space. Hence this process occurs.

Now it is easy to reverse back the process and generate sugar back from the solution. The vaporization process, along with condensation and crystallization, will bring back the molecule. Hence now we know when does a physical change occur.

Frequently Asked Questions (FAQs)

Name two types of changes that can occur.

There are two types of changes that are known to humans; chemical change and physical change.

The change that forms a new substance by altering the chemical composition of the substance is said to be a chemical change. All the modifications that happen in the physical characters are inferred as physical change. There is no formation of new substances during the physical change.

Explain the physical change.

The changes happening about the physical properties of the object, substance, or compound is said to be physical change.

It involves changes in size, shape, color, odor, temperature, or pressure. Physical changes are said to be temporary changes. They can be reversed to bring back to the primary state, and some are irreversible too. E.g.:- broken glass, tearing paper, chopping vegetables.

When does a physical change occur?

Physical changes can be reversed or stay irreversible depending upon the situation.

A physical change occurs when there is any kind of alteration in the physical properties of the object. The changes can be just temporary or become irreversible. These changes do not lead to the formation of any new substance.

Is physical change temporary or permanent change?

Physical changes can be reversed back to their initial state by physical means.

Since physical change can be reversed, it is said to be a temporary change. The chemical change is known to be a permanent change. But remember, not all physical changes are reversible, like cutting trees into logs.

How to know the physical change has taken place?

Since the physical change brings changes in the physical properties of the substance, it can easily be seen.

If you see a change in any physical characteristics of the object, know that physical change has taken place. For example, when you drop a glass, it breaks into smaller pieces. The size and shape get deformed on hitting the floor. Hence physical change has occurred.

What are the signs of physical changes?

The change in physical properties is classified as physical change.

The signs of physical change are shape, size, color, matter, odor, temperature, and pressure. Any change in the following properties indicates that the physical change has taken place. These changes can clearly be observed by us and in the most cases are reversible.

Also Read:

How Physical Changes Can Be Reversed: Detailed Analysis

January 21, 2024November 7, 2021 by Rabiya Khalid

The physical changes that occur about the state, shape, or size of an object are reversible. Let us know how physical changes can be reversed.

Some of the substances which change physically can be brought back to their original state by physical means. There are few physical changes that can not be reversed at all. When there is a change in the state of the substance, the reversibility becomes easier.

We know that there are two types of changes that occur. One is a physical change, and the other is a chemical change. Chemical changes occur when a totally new substance is formed and is generally a permanent change. In comparison, physical changes are those in which only the physical properties alter. The total internal energy remains the same, and hence they are termed as temporary changes.

Physical changes can either reverse or become irreversible. We have already reviewed irreversible physical change examples. Now let us know how physical change can be reversed. Usually, when there is a change in the state of the matter, we can bring back the initial substance by physical means.

How physical changes can be reversed — Image Credit: https://simple.wikipedia.org/wiki/File:Melting_icecubes.gif

To further understand it let us look at the example of water and ice. On freezing, water changes into ice. Water is the liquid state, and ice is the crystalline solid. Both ice and water have the same chemical formula as H₂O. So it is obvious that there have been no changes in the internal energy and composition of water. Now to reverse ice into the water, we just have to melt the ice. Similarly, we can change water into water vapor and then back to the water by condensation process.

Let’s take the second case of salt and water solution. On adding salt and stirring it, we obtain a solution. Some might confuse it as a chemical change. But that is not the case. The solution obtained is still a physical change because when we add the salt, no change occurs in the chemical composition of water. Moreover, this process can be reversed.

On boiling the solution, the water starts changing into water vapor. And gradually it evaporates in the atmosphere. When all the water escapes away, the residue left behind is salt. This process is one of the commercial ways to manufacture salt. So, we can get back salt by the boiling process.

stone 1021325 1280 — Image Credit: https://pixabay.com/photos/stone-plants-rock-cracked-cracks-1021325/

Now we get the idea of how physical changes can be reversed. But not all changes are reversible. We have already seen that physical changes can be reversed and, in some cases, stay irreversible. Now let us try to reverse an irreversible physical change.

When physical factors like rain, sunlight, and wind continuously act on the rock, they start cracking. The cracks make space for these factors to break down the rocks more deeply. Slowly the rocks get deformed and change into the soil. The rock and soil both have the same composition, and hence it is a physical change. With any of the physical and chemical, this process can not be reversed back.

So now we know that reversible physical change can be brought back to its original state by physical means.

Frequently Asked Questions (FAQs)

Can physical change be reversed?

Physical changes are those changes that occur in the state, shape, size, or any such physical parameters of the object.

In many cases, physical changes are temporary that can be brought back to their initial state. This is because when a body undergoes a physical change, there is no change in its internal energy. Hence we infer that physical change can be reversed.

Is it easy to reverse physical changes?

Physical changes can be brought back into their original state, i.e., they are reversible.

In a physical change, the changes occur in the size, shape, or state of the object. The chemical composition and the total internal energy remain the same. Hence it becomes easier to reverse back the change.

Can all physical changes be reversed?

The changes that occur in the object can either be reversed or become irreversible.

The physical changes can be both reversible and irreversible. Folding clothes is a reversible change. At the same time, cutting trees into logs is an irreversible change. Therefore not all physical changes are reversible, and not every irreversible change is a chemical change.

What is easier to reverse, physical change or chemical change?

Changes can be of two types; physical changes and chemical change.

The chemical changes are irreversible and can’t be brought back into their initial state. Physical change can be reversed, and some of them are irreversible too. Since chemical change cannot be reversed at all, in comparison, physical change becomes easier to reverse and bring to the original state.

How physical changes can be reversed

We know that physical changes can be reversed and therefore termed as a temporary change.

When there is a change in the state of an object or substance, the physical change that occurs can be reversed back. When this happens using physical means, the change can be reversed, and the initial substance can be brought back.

Give an example of reversible physical change?

Physical changes can be reversed to obtain the initial object. Hence it is also known as a temporary change.

An example of reversible physical change is water changing into ice. Both ice and water have the same chemical formula as H2O. Now on melting, ice changes back into the water. Therefore it is a reversible change.

Also Read:

Physical Irreversible Change Example: Detailed Analysis

January 21, 2024November 4, 2021 by Rabiya Khalid

Physical changes can either be reversible or irreversible. Let us discuss some physical irreversible change examples.

Cutting trees into logs
Broken glass
Growth of tree
Pulverizing a rock
Mixing paint colors
Cracking an egg
Shredding paper
Sharpening pencil
Stitching dress out of a piece of fabric
Rock erosion
Grinding wood into sawdust
Chopping vegetables

Cutting trees into logs

tree 576846 1280 — Cutting trees into log is a physical change
Image Credit: https://pixabay.com/vectors/tree-log-fallen-cartoon-nature-576846/

This is one of the most common physical irreversible change example. On chopping trees to form logs, there is no involvement of internal energy. The chemical elements of the wood and the logs are just the same. It is clearly seen that only the size and shape are changed. Hence it is an example of physical change. But it is not a temporary change that is not reversible. Chopping a tree into small pieces of wood or logs is an irreversible change as we cannot obtain the whole tree back from these logs. Once the cutting is done, it becomes a permanent change.

Broken glass

When we drop a bowl made of glass, it accidentally gets broken into many smaller pieces. The small pieces of glass and the bowl as a whole are of the same material. We can find that the glass’s internal energy and chemical reactivity remains the same. But can we get back the bowl from the shattered and broken pieces of glass? The answer would be no. Of course, we can not bring back the bowl. Even if we try to weld the glass to join the pieces, we won’t get the exact bowl. So broken glass is an example of irreversible physical change.

Growth of tree

ezgif 6 41b2d38c58d2 — Image Credit: https://pixabay.com/vectors/branch-grow-growing-leaf-nature-2029756/

The growth of a small plant into a big tree is a unique chance. It is an example of both physical and chemical change; as for the growth of the tree, a chemical reaction such as photosynthesis occurs. The growth of a tree leads to stretching and growth of its branches and heights; hence it is also a physical change since we can not reverse and bring a seedling or a small plant back from a tree, so it is an irreversible change.

Pulverizing a rock

Breaking down the rocks into smaller and minute particles by either crushing, grinding, or beating them is known as pulverizing. The rock gets changed into powder form, but the chemical reactivity before and after the pulverization remains the same. Therefore, pulverizing a rock is classified as a physical change. Further, once the rock is crushed down, it can not be undone; that is, we can not bring it back to its original position. So we can say that pulverizing a rock is one of the physical irreversible change examples.

Mixing paint colors

ezgif 6 4e7f6c5c561d — Mixing Paint colors
Image Credit: https://pixabay.com/vectors/palette-paints-colors-mixing-33882/

Mixing paint colors to obtain a new color is another example of irreversible physical change. When paints are mixed, no new substance is formed; only the color is changed. The zero change in the internal energy of the object makes it a physical change. Secondly, once a new color is obtained, we can not bring back the exact same colors no matter what color we obtain. Therefore mixing paints together is an irreversible change.

Cracking an egg

A cracked egg is the simplest example of physical change. When the shell is cracked, the egg comes out, as only the shape is changed; it is considered as a physical change. Further, we know that it is in no way practical to make the cracked eggshell go back to its initial position. Also, it is obvious that in no way can it be put back into the shell. So cracked egg is an irreversible physical change.

Shredding paper

physical irreversible change example — Image Credit: https://pixabay.com/vectors/shredder-document-paper-shredder-311638/

We all know that shredding or tearing paper is a physical change, as only the size and shape of the paper are changed without altering its chemical composition. A sheet of paper is changed into strips of paper. Now once the paper is shredded into strips, it becomes impossible to bring back the original sheet. Some might question that by sticking the paper strips with tape, we can recover the paper. But that’s not the reality, the shape and size remain distorted to some extent, and the exact original piece of paper can not be restored. Hence it is also one of the physical irreversible change examples.

Sharpening pencil

When we sharpen the pencil every time, its size gets reduced. The change in the size of the pencil makes it a physical change. Secondly, since the process can not be undone, the pencil size can not be increased; it is irreversible. The sharpener only cuts the wood or graphite of which the pencil is made. It brings no change in the atomic structure or composition of wood and graphite.

Stitching dress out of a piece of fabric

For stitching a dress out of a piece of fabric, it has to be in different shapes. Since the dress is made of fabric, its chemical nature would be the same. Firstly as only the shape and size of the fabric are altered, it is a physical change. Now once the dress is stitched, can the process be reversed? Of course not. We can bring back the initial fabric out of the piece of the dress. Even if we cut out the stitches, some of the parts of the fabrics can not be undone. Hence the stitching of a dress out of a piece of fabric is a physical irreversible change example.

Rock erosion

arid 21799 1280 — Image Credit: https://pixabay.com/photos/arid-cracked-erosion-cracks-desert-21799/

Erosion is a natural phenomenon involving removing natural resources from their initial positions due to weathering. The rock erosion is the same but with one exception; it does not involve the movement of rocks. Rock erosion or weathering is the phenomenon in which the rocks are broken down into smaller pieces and change into the soil. The chemical constituents of the rock before and after the erosion remains the same. So it is considered as a physical change. Once the rock is changed into the soil, it can not be reversed back; hence it is an irreversible physical change.

Grinding wood into sawdust

The grinding of the wood changes it into sawdust. The sawdust has the same atomic stability and chemical structure as the wood. Due to no change in internal energy, it is termed as physical change. During this process, the wood just changes into minute powder. It is impossible to generate the wood from the sawdust; therefore, it is also an irreversible change.

Chopping vegetables

ezgif 6 01927365cbe2 — Image Credit: https://pixabay.com/photos/cucumber-food-vegetable-78789/

Chopping vegetables is another physical irreversible change example. When we cut or slice vegetables into small pieces for cooking, only the size is changed, and everything else like chemical constituents remains the same. Also, once the vegetables are chopped, they can not be brought back into their original state. Since this process can not be reversed using any method, therefore, it is an irreversible change.

All these are the physical irreversible change examples. Through these, we get to know that physical change does not necessarily have to be reversible; it can be irreversible too. Now we can define physical change as the reversible or irreversible change that occurs about the object’s physical properties.

Also Read:

Is Physical Change Reversible: Detailed Analysis

January 21, 2024November 2, 2021 by Rabiya Khalid

In reaction, when the changes occur about the reactants’ physical characteristics, they are said to be a physical change. Let’s know if this change is reversible.

The answer to the question is physical change reversible or not is yes. Yes, the physical changes are reversible in nature and can be brought to their original state. Hence we can say that the physical changes are temporary, and there is no change in their chemical properties.

On reaction, the changes that occur can be differentiated into physical changes and chemical changes. The changes in the physical properties of the object or compound are said to be a physical changes. At the same time, a chemical change is defined as changes in chemical properties. Tearing up paper is the basic example of physical change. On tearing paper gets smaller in size, but there is no change in the chemical properties.

Physical change is reversible changes that are it can be brought back to its original state. It usually involves a change in the shape, size, and state of the object. Since all these changes can be reversed, the physical change is also termed as the temporary change. Stretching of a rubber band, balloon inflation, and water boiling are all examples of reversible physical change.

paper 6276204 1280 — Image Credit: https://cdn.pixabay.com/photo/2021/05/23/13/23/paper-6276204_1280.png

Why is physical change reversible

When the bonds that keep the elements intact together break, the changes occur in the compound’s chemical properties. The bond on breaking brings about the internal energy of the body. In a physical change, all these phenomena do not occur. The name itself suggests that the changes occur in the physical properties that are size, shape, or state. These changes do not break bonds, and hence, the internal energy remains the same. Therefore the physical change is reversible in nature.

To understand the reversibility of physical change, let us see the example of water, on cooling liquid water changes into ice that is the solid form. From the liquid state, water has changed into a solid-state that is changing has happened in the state of the water. On melting, ice can again change into water. We know that the chemical formula for ice and water is H₂O, which means there is no change in chemical property. Hence the physical change that takes place on cooling water can be reversed on melting.

In the same when we heat water, it changes into water vapors. The chemical formula of both of them remains H₂O. We can reverse back water vapors into the water by condensation process. This whole conversion of water into ice and vapors and back to its original form explains the reversibility of physical changes.

Are physical changes always reversible

We have understood is physical change reversible or not. But is it always reversible? The answer to this is No. The physical change is not necessarily always reversible. Some of the changes can not be brought back to their initial stage.

To understand this, let us take the example of raw egg. When we break it down, the inner material comes out. The whole thing still remains the same, and there is no change in the chemical composition of the egg. Therefore it is a physical change. But can we put back the yolk into the eggshell? The answer is No. We cannot reverse this change; hence it is an irreversible physical change.

ezgif 7 8664fe84c653 — Growth of a tree
Image Credit: https://pixabay.com/vectors/tree-trunk-nature-leaves-branches-576836/

Therefore we understand now that physical change does not always have to be reversible. There are a lot of physical changes that can not be brought back. There are many who says the growth of a tree is completely chemical change as it is irreversible, but that is not the case. It is both chemical as well physical change. The growth of trees is an example of irreversible physical change.

We know now that not all irreversible changes are chemical changes; they can also be physical changes. Abd physical change not always has to be reversible.

Frequently Asked Questions (FAQs)

What are the two types of changes?

On reaction, there can occur two kinds of changes; chemical change and physical change.

When a reaction takes place, and a completely new substance is formed with different chemical properties, the change is said to be a chemical change. When no new substance is formed and its properties remain the same before and after the reaction, the change is known as physical change.

What is a physical change?

The changes in the physical properties of the substance or object are known as physical changes.

Physical changes are temporary that do not involve any change in the internal energy of the object. They generally bring changes in the size, shape, and state of matter. These types of changes are generally temporary.

Give an example of physical change.

The forces that bring about changes in a physical state if the object is said to be physical changes.

To explain the physical change, let’s suppose you have a large piece of cloth and you cut it into small pieces. Here the change has occurred in the size of the cloth. So this is an example of physical change. The freezing of water is also an example of physical change.

Is physical change reversible? Explain

Physical changes are those which does not involve any interference with the internal energy of the object.

Since the internal energy remains the same before and after the reaction, there is no change in the object’s chemical composition. Therefore the physical changes are reversible in nature. That is, they can be brought back to their original state, for example, freezing of water into ice.

Is physical change always reversible?

No, physical change is not always reversible; it can be irreversible too. There are many examples of irreversible physical change.

The cutting of trees into logs is a basic example of physical change. Since both are wood and there is no change in their composition, they are physical changes. But we cannot bring back the tree from the log, so it is an irreversible change.

Also Read:

RPM To Angular Velocity: 5 Answers You Should Know

January 21, 2024October 31, 2021 by Rabiya Khalid

The concept of RPM (revolutions per minute) and angular velocity is essential in understanding the rotational motion of objects. RPM refers to the number of complete revolutions an object makes in one minute, while angular velocity measures the rate at which an object rotates in radians per second. To convert RPM to angular velocity, we need to multiply the RPM by 2π/60 to obtain the angular velocity in radians per second. This conversion factor accounts for the fact that there are 2π radians in one complete revolution and 60 seconds in one minute.

Key Takeaways

RPM	Angular Velocity (rad/s)
100	10.47
200	20.94
300	31.41
400	41.88
500	52.35

Understanding Angular Velocity

Angular velocity is a fundamental concept in physics that helps us understand the rotational motion of objects. It describes how fast an object is rotating or spinning around a fixed axis. In this article, we will explore the definition and concept of angular velocity, its relationship with rotational motion, and the unit of measurement used to quantify it.

Definition and Concept of Angular Velocity

Angular velocity is defined as the rate of change of angular displacement with respect to time. It measures how quickly an object is rotating or spinning. Just like linear velocity measures how fast an object is moving in a straight line, angular velocity measures how fast an object is rotating around an axis.

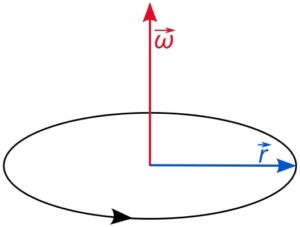
To better understand angular velocity, let’s consider a wheel rotating. As the wheel spins, different points on its rim move at different speeds. The angular velocity tells us how fast each point is moving in terms of the angle covered per unit of time. It is commonly denoted by the Greek letter omega (ω).

Relationship between Angular Velocity and Rotational Motion

Angular velocity is closely related to rotational motion. It helps us analyze and describe various aspects of objects in circular or rotational motion. By understanding angular velocity, we can determine the rotational speed, revolutions per minute (RPM), and angular speed of an object.

The relationship between angular velocity and linear velocity is also significant. Linear velocity is the speed of an object moving along a straight line, while angular velocity is the speed of an object rotating around an axis. The two are related through the concept of radius. The linear velocity of a point on a rotating object is equal to the product of its angular velocity and the distance from the axis of rotation.

Angular Velocity Unit: Radian per Second

Angular velocity is typically measured in radians per second (rad/s). Radians are a unit of measurement for angles, and they are particularly useful when dealing with circular motion. One radian is equal to the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle.

To convert angular velocity from degrees per second to radians per second, we can use the conversion factor of π/180. This conversion factor accounts for the fact that there are 2π radians in a complete circle and 360 degrees in a circle.

In summary, understanding angular velocity is crucial for comprehending rotational motion in physics. It allows us to analyze the speed and motion of rotating objects, and it is measured in radians per second. By exploring the relationship between angular velocity and rotational motion, we can gain insights into the dynamics of circular motion and solve various motion equations in rotational kinematics.

Converting RPM to Angular Velocity

Explanation of the Conversion Process

When it comes to rotational motion, one of the key parameters we often encounter is the rotational speed, commonly measured in revolutions per minute (RPM). However, in many cases, it is more convenient to work with angular velocity, which is measured in radians per second (rad/s). Converting RPM to angular velocity allows us to express rotational motion in a more universal and precise manner.

To understand the conversion process, we first need to establish the relationship between revolutions and radians. In circular motion, one revolution corresponds to a complete 360-degree rotation. Since there are 2π radians in a full circle, we can say that one revolution is equal to 2π radians.

Relationship between Revolutions and Radians

One revolution = 2π radians
Half a revolution = π radians
Quarter of a revolution = π/2 radians

Now that we know the relationship between revolutions and radians, we can derive the conversion formula.

Conversion Formula: 1rpm = 2π/60 rad.s^-1

To convert RPM to angular velocity, we use the conversion factor of 2π/60 rad/s. This factor accounts for the fact that there are 60 seconds in a minute and 2π radians in one revolution.

To apply the conversion formula, we simply multiply the given RPM value by the conversion factor. The resulting value will be the angular velocity in rad/s.

Example: Converting 80 RPM to Angular Velocity

Let’s take an example to illustrate the conversion process. Suppose we have a wheel rotating at a speed of 80 RPM. To find the corresponding angular velocity, we can use the conversion formula:

Angular velocity = 80 RPM * (2π/60 rad/s)

Simplifying the equation, we get:

Angular velocity = 80 * 2π/60 rad/s

Calculating the value, we find that the angular velocity is approximately 8.377 rad/s.

By converting RPM to angular velocity, we can better understand and analyze rotational motion in terms of radians per second. This conversion allows us to apply the principles of physics and kinematics to solve problems related to rotational motion, such as determining rotational velocity, linear velocity, tangential velocity, and motion equations in rotational kinematics.

Remember, the conversion formula of 1rpm = 2π/60 rad/s is a useful tool when dealing with circular velocity, wheel rotation, spin rate, or any other scenario involving rotational speed.

Tools for Conversion

RPM to Angular Velocity Converter

When it comes to understanding rotational motion and circular velocity, one of the key concepts to grasp is the conversion between RPM (rotations per minute) and angular velocity. This conversion is essential in various fields, including physics, kinematics, and engineering. To simplify this process, we have developed the RPM to Angular Velocity Converter tool.

To use the RPM to Angular Velocity Converter, simply input the value of RPM into the designated field. The converter will then calculate the corresponding angular velocity in radians per second. This conversion factor is crucial for understanding the relationship between rotational speed and angular speed.

In circular motion, angular velocity represents the rate at which an object rotates around a fixed axis. It is measured in radians per second (rad/s). By converting RPM to angular velocity, we can determine the speed at which an object is rotating and its angular frequency.

To better understand the concept, let’s consider an example. Suppose we have a wheel rotating at 120 RPM. Using the RPM to Angular Velocity Converter, we can determine the angular velocity by inputting the value of 120 RPM. The converter will then provide us with the corresponding angular velocity in radians per second.

RPM to Angular Velocity Calculator

In addition to the RPM to Angular Velocity Converter, we also offer the RPM to Angular Velocity Calculator. This tool provides a convenient way to calculate the angular velocity based on the given RPM value. It is particularly useful when you need to perform multiple calculations or when you want to quickly verify your results.

To use the RPM to Angular Velocity Calculator, you simply need to enter the RPM value into the designated field. The calculator will then instantly display the corresponding angular velocity in radians per second. This allows you to quickly obtain the desired conversion without the need for manual calculations.

Understanding the relationship between RPM and angular velocity is crucial in various applications. For example, in rotational kinematics, the angular velocity is used to determine the rotational velocity of an object. It is also related to the linear velocity and tangential velocity of an object in circular motion.

By utilizing the RPM to Angular Velocity Converter and Calculator, you can easily perform the necessary conversions and gain a better understanding of rotational motion. These tools provide a simple and efficient way to convert between RPM and angular velocity, making it easier to analyze and solve problems related to circular velocity, wheel rotation, spin rate, and more.

Remember, whether you are studying physics, working on engineering projects, or simply curious about rotational motion, our RPM to Angular Velocity Converter and Calculator are here to assist you in your calculations.

Understanding RPM and Angular Speed

Rotational speed is an important concept in physics that helps us understand the motion of objects in circular or rotational motion. One common unit used to measure rotational speed is revolutions per minute (RPM). On the other hand, angular speed is a measure of how quickly an object rotates around a fixed axis. In this article, we will explore the relationship between RPM and angular speed, as well as how angular speed affects the rotation of a body.

Relationship between RPM and Angular Speed

The relationship between RPM and angular speed is quite straightforward. RPM measures the number of complete revolutions an object makes in one minute, while angular speed measures the rate at which an object rotates in radians per second. To convert from RPM to angular speed, we need to use a conversion factor.

The conversion factor between RPM and angular speed is given by the formula:

Angular Speed (in radian per second) = RPM * (2π/60)

Here, 2π represents the number of radians in one complete revolution, and 60 is the number of seconds in one minute. By multiplying the RPM value by this conversion factor, we can obtain the corresponding angular speed in radian per second.

How Angular Speed Affects the Rotation of a Body

Angular speed plays a crucial role in determining the motion of a rotating body. It affects various aspects of rotational motion, including the rotational velocity, linear velocity, and tangential velocity of the object.

The rotational velocity of an object is directly proportional to its angular speed. As the angular speed increases, the object rotates faster, covering a larger angular displacement in a given time. This relationship can be described by the equation:

Rotational Velocity = Angular Speed * Radius

where the radius represents the distance from the axis of rotation to a point on the object.

Similarly, the linear velocity of a point on a rotating object is also influenced by the angular speed. The linear velocity is given by the equation:

Linear Velocity = Angular Speed * Radius

This equation shows that the linear velocity of a point on the object is directly proportional to the angular speed and the distance from the axis of rotation.

Lastly, the tangential velocity of a point on a rotating object is equal to the linear velocity of that point. Therefore, the tangential velocity is also affected by the angular speed. As the angular speed increases, the tangential velocity of the point increases as well.

In summary, understanding the relationship between RPM and angular speed is essential in analyzing the motion of rotating objects. By converting between these units and considering the effects of angular speed on rotational and linear velocities, we can gain valuable insights into the dynamics of circular motion.

Now that we have explored the relationship between RPM and angular speed, as well as how angular speed affects the rotation of a body, we can apply these concepts to solve various problems in rotational kinematics and circular motion. Whether it’s calculating the rotational velocity of a spinning wheel or analyzing the spin rate of a cycle per second, the motion equations and principles of angular speed will guide us in understanding the dynamics of rotational motion.

Exploring the Connection between RPM and Angular Velocity

Angular velocity and revolutions per minute (RPM) are two important concepts in physics that describe the rotational motion of an object. Understanding the relationship between RPM and angular velocity is crucial in various fields, including mechanics, engineering, and even sports. In this article, we will delve into the factors that influence this relationship and explore the conversion between RPM and angular velocity.

Factors Influencing the RPM-Angular Velocity Relationship

Several factors play a role in determining the relationship between RPM and angular velocity. Let’s take a closer look at each of these factors:

Conversion Factor: To convert RPM to angular velocity, we need to use a conversion factor. This factor depends on the units used to measure RPM and angular velocity. For example, if RPM is measured in revolutions per minute and angular velocity is measured in radians per second, the conversion factor is 2π/60. This conversion factor allows us to relate the linear motion of an object to its rotational motion.
Circular Motion: The relationship between RPM and angular velocity becomes evident when considering circular motion. When an object moves in a circular path, it undergoes both linear and rotational motion simultaneously. The angular velocity describes the rate at which the object rotates around its axis, while the RPM indicates the number of complete rotations the object makes in one minute.
Rotational Kinematics: The motion equations for rotational kinematics provide a mathematical framework to understand the relationship between RPM and angular velocity. These equations relate the angular displacement, angular velocity, and angular acceleration of an object in rotational motion. By manipulating these equations, we can determine the angular velocity of an object given its RPM or vice versa.
Linear Velocity: The linear velocity of an object on the edge of a rotating wheel or disk is related to its angular velocity. This relationship is given by the formula v = rω, where v represents the linear velocity, r is the radius of the wheel, and ω is the angular velocity. As the angular velocity increases, the linear velocity also increases, resulting in faster motion along the edge of the wheel.
Tangential Velocity: Tangential velocity is another term used to describe the linear velocity of an object moving in a circular path. It represents the speed of an object at a specific point on its circular trajectory. The tangential velocity is directly proportional to the angular velocity and the radius of the circular path. As the angular velocity increases, the tangential velocity also increases.
Spin Rate: The spin rate of an object refers to the number of complete rotations it makes in a given time period. This spin rate is commonly measured in RPM. By knowing the spin rate, we can determine the angular velocity of the object using the conversion factor mentioned earlier.

Understanding the connection between RPM and angular velocity is essential in various applications. Whether it’s analyzing the performance of a rotating machine or calculating the speed of a spinning wheel, knowing how these two concepts relate to each other allows us to make accurate predictions and calculations in the field of physics and kinematics.

In conclusion, the relationship between RPM and angular velocity is influenced by factors such as the conversion factor, circular motion, rotational kinematics, linear velocity, tangential velocity, and spin rate. By understanding these factors and their interplay, we can gain a deeper understanding of rotational motion and its connection to linear motion.

Converting Revolutions per Minute to Angular Velocity

Detailed Explanation of the Conversion Steps

Converting revolutions per minute (RPM) to angular velocity is a fundamental concept in physics and kinematics. It allows us to understand the rotational motion of objects and calculate their angular speed in radians per second. By converting RPM to angular velocity, we can analyze circular motion, rotational kinematics, and various other aspects of rotational dynamics.

To convert RPM to angular velocity, we need to use a conversion factor. The conversion factor is derived from the relationship between the number of revolutions and the number of radians in a complete circle. In one revolution, there are 2π radians. Therefore, the conversion factor is 2π radians per revolution.

To convert RPM to angular velocity, we can use the following formula:

Angular Velocity (in radians per second) = RPM * (2π radians/revolution) * (1 minute/60 seconds)

Let’s understand this conversion process with an example. Suppose we have a wheel rotating at a speed of 120 RPM. We can calculate its angular velocity as follows:

Angular Velocity = 120 RPM * (2π radians/revolution) * (1 minute/60 seconds)

Simplifying the equation, we get:

Angular Velocity = 120 * (2π/60) radians per second

Calculating the value, we find that the angular velocity of the wheel is approximately 12.57 radians per second.

Importance of Understanding the Units Involved

Understanding the conversion from RPM to angular velocity is crucial in various fields, especially in physics and engineering. Here are a few reasons why it is important to grasp this concept:

Analysis of Rotational Motion: Converting RPM to angular velocity allows us to analyze the rotational motion of objects. By understanding the angular speed in radians per second, we can determine the rate at which an object is rotating and study its behavior.
Application in Circular Motion: Angular velocity is essential in studying circular motion. It helps us calculate the rotational velocity and the linear velocity of objects moving in circular paths. These calculations are vital in fields such as astronomy, mechanics, and sports.
Motion Equations: Converting RPM to angular velocity is necessary when dealing with motion equations involving rotational kinematics. By converting the units, we can apply the appropriate formulas and solve problems related to rotational dynamics.
Interchangeability with Linear Velocity: Understanding the conversion between RPM and angular velocity allows us to relate rotational motion to linear motion. By knowing the tangential velocity of an object in circular motion, we can determine its linear velocity and vice versa.

By grasping the concept of converting RPM to angular velocity, we can gain a deeper understanding of rotational dynamics and its applications in various fields. It enables us to analyze the spin rate, cycle per second, and circular velocity of rotating objects, providing valuable insights into their behavior and characteristics.

Remember, RPM and angular velocity are interconnected, and being able to convert between the two units is essential for anyone studying or working with rotational motion.

RPM to Angular Velocity in Rad/s

Understanding the Unit of Radian per Second (rad/s)

When it comes to rotational motion, understanding the unit of radian per second (rad/s) is crucial. Radian per second is a unit used to measure angular velocity, which represents how fast an object is rotating. It is derived from the concept of circular motion, where one complete revolution around a circle is equal to 2π radians.

In physics and kinematics, angular velocity is often expressed in rad/s because it provides a more accurate representation of the rotational speed. Unlike revolutions per minute (RPM), which measures the number of complete rotations in a minute, rad/s focuses on the actual angular displacement per unit of time. This unit allows us to analyze rotational motion more precisely and make calculations using motion equations specific to rotational kinematics.

Significance of Expressing Angular Velocity in Rad/s

Expressing angular velocity in rad/s has several significant advantages. Firstly, it allows for easier comparison and conversion between different units of rotational speed. By using the conversion factor of 2π rad/s = 1 revolution per second, we can easily convert between rad/s and RPM.

Secondly, rad/s provides a direct link between angular velocity and linear velocity. In circular motion, the linear velocity of an object on the edge of a rotating wheel is equal to the product of its angular velocity (in rad/s) and the radius of the wheel. This relationship is crucial in understanding the tangential velocity of objects in rotational motion.

Lastly, expressing angular velocity in rad/s enables us to apply the principles of frequency and period. Angular frequency, measured in rad/s, is the number of complete cycles per second. It is related to angular velocity through the equation ω = 2πf, where ω is the angular frequency and f is the frequency in cycles per second.

Example: Converting 45 RPM to Angular Velocity

Let’s take an example to understand how to convert RPM to angular velocity in rad/s. Suppose we have a wheel rotating at a speed of 45 RPM. To convert this to rad/s, we can use the conversion factor mentioned earlier: 2π rad/s = 1 revolution per second.

Using this conversion factor, we can calculate the angular velocity as follows:

Angular velocity (in rad/s) = 45 RPM * (2π rad/s) / (1 revolution per minute)

Simplifying the equation, we get:

Angular velocity = 45 * 2π / 60 rad/s

Angular velocity ≈ 4.71 rad/s

Therefore, a wheel rotating at 45 RPM has an angular velocity of approximately 4.71 rad/s.

By converting RPM to rad/s, we can better understand the rotational motion of objects and apply the principles of angular velocity in various physics and engineering applications. Whether it’s analyzing the spin rate of a wheel or calculating the circular velocity of an object, expressing angular velocity in rad/s provides a more accurate and comprehensive representation of rotational speed.

How to Find Angular Velocity from RPM

Exploring the Formula for Converting RPM to Angular Velocity

When it comes to understanding rotational motion, one important concept to grasp is the relationship between rotational speed and angular velocity. Rotational speed is commonly measured in revolutions per minute (RPM), while angular velocity is measured in radians per second (rad/s). In this guide, we will explore the formula for converting RPM to angular velocity and provide some tips for calculating angular velocity accurately.

To convert RPM to angular velocity, we need to use a conversion factor. The conversion factor is derived from the relationship between the circumference of a circle and the angle it subtends. In circular motion, one revolution corresponds to a complete circle, which is equivalent to 2π radians. Therefore, the conversion factor is 2π/60, since there are 60 seconds in a minute.

To calculate angular velocity (ω) from RPM, we can use the following formula:

ω = (2π/60) * RPM

Let’s say we have a wheel rotating at 120 RPM. To find its angular velocity, we can substitute the value of RPM into the formula:

ω = (2π/60) * 120

Simplifying the equation, we get:

ω = 4π rad/s

So, the angular velocity of the wheel is 4π rad/s.

Tips for Calculating Angular Velocity Accurately

Calculating angular velocity accurately is crucial in various fields of physics, such as kinematics and rotational motion. Here are some tips to help you calculate angular velocity with precision:

Understand the units: Make sure you are familiar with the units of rotational speed (RPM) and angular velocity (rad/s). Knowing the conversion factor and how to apply it correctly is essential.
Use the correct formula: The formula ω = (2π/60) * RPM is specifically used to convert RPM to angular velocity. Be sure to use this formula when performing calculations.
Convert units if necessary: If you are given rotational speed in units other than RPM, such as degrees per second or cycles per second, you may need to convert them to RPM before applying the formula. Use the appropriate conversion factors for accurate results.
Consider linear velocity: Angular velocity is related to linear velocity, which is the tangential velocity of an object moving in a circular path. If you know the radius of the circular path, you can use the formula v = ω * r to calculate the linear velocity.
Practice with motion equations: Familiarize yourself with the motion equations for rotational kinematics. These equations can help you solve problems involving angular velocity, acceleration, and time.

By following these tips, you can enhance your understanding of angular velocity and accurately calculate it in various scenarios. Remember to double-check your calculations and units to ensure precision in your results.

Now that you have a better understanding of how to find angular velocity from RPM and some tips for accurate calculations, you can confidently tackle problems involving rotational motion and circular velocity. Keep practicing and exploring the fascinating world of physics!

Frequently Asked Questions

What is the Relationship between Angular Velocity and RPM?

Angular velocity and RPM (revolutions per minute) are related to each other in circular motion. Angular velocity represents the rate at which an object rotates, while RPM measures the number of complete revolutions an object makes in one minute. The relationship between the two can be expressed using a conversion factor.

How do I Convert RPM to Angular Velocity in Radians per Second?

To convert RPM to angular velocity in radians per second, you can use the following formula:

Angular Velocity (in radians per second) = RPM * (2π/60)

Here, 2π represents the number of radians in one complete revolution, and 60 represents the number of seconds in one minute. By multiplying the RPM by the conversion factor, you can obtain the angular velocity in radians per second.

How do I Calculate the Angular Velocity for 80 RPM?

To calculate the angular velocity for 80 RPM, you can use the conversion formula mentioned earlier:

Angular Velocity (in radians per second) = 80 * (2π/60)

Simply substitute the value of 80 RPM into the formula and perform the calculation to find the angular velocity in radians per second.

Is there a Converter for RPM to Angular Velocity?

Yes, there are online converters available that can help you convert RPM to angular velocity. These converters usually require you to input the RPM value, and they will provide the corresponding angular velocity in radians per second. You can easily find these converters by searching online.

What is the Angular Velocity for 20 RPM?

To find the angular velocity for 20 RPM, you can use the same conversion formula mentioned earlier:

Angular Velocity (in radians per second) = 20 * (2π/60)

By substituting the value of 20 RPM into the formula and performing the calculation, you can determine the angular velocity in radians per second.

What is the Relationship between RPM and Angular Speed?

RPM and angular speed are closely related in circular motion. Angular speed represents the rate at which an object rotates, similar to angular velocity. The only difference is that angular speed is measured in radians per unit of time, while RPM measures the number of complete revolutions per minute. The relationship between RPM and angular speed can be established using the conversion factor mentioned earlier.

How can I Convert Revolutions per Minute to Angular Velocity?

To convert revolutions per minute (RPM) to angular velocity, you can use the conversion formula:

Angular Velocity (in radians per second) = RPM * (2π/60)

By multiplying the RPM value by the conversion factor, you can obtain the angular velocity in radians per second.

Is there a Calculator to Convert RPM to Angular Velocity?

Yes, there are online calculators available that can help you convert RPM to angular velocity. These calculators typically require you to input the RPM value, and they will provide the corresponding angular velocity in radians per second. You can easily find these calculators by searching online.

Remember, understanding the relationship between rotational speed, revolutions per minute, and angular velocity is essential in the study of circular motion and rotational kinematics. By utilizing the appropriate conversion factors and motion equations, you can easily convert between RPM and angular velocity to analyze various aspects of rotational motion.

How do I Convert Rev/min to Angular Velocity?

Converting revolutions per minute (RPM) to angular velocity is a straightforward process that involves a simple conversion factor. Angular velocity is a measure of how quickly an object rotates or moves in a circular path. It is commonly used in physics and kinematics to describe rotational motion.

To convert RPM to angular velocity, you need to multiply the rotational speed by a conversion factor. The conversion factor depends on the units you want to convert to. In this case, we want to convert RPM to radians per second (rad/s), which is a commonly used unit for angular velocity.

The conversion factor for converting RPM to rad/s is given by:

Conversion Factor: 1 RPM = (2π/60) rad/s

This conversion factor is derived from the fact that there are 2π radians in one revolution and 60 seconds in one minute. By multiplying the RPM value by this conversion factor, we can obtain the corresponding angular velocity in rad/s.

Let’s take a specific example to illustrate this conversion.

What is the Angular Velocity for 2500 RPM?

To find the angular velocity for 2500 RPM, we can use the conversion factor mentioned earlier.

Given:
Rotational speed (RPM) = 2500 RPM

Conversion:
Angular velocity (rad/s) = 2500 RPM * (2π/60) rad/s

Simplifying the equation, we get:

Angular velocity (rad/s) = 2500 * (2π/60) rad/s

Calculating this expression, we find:

Angular velocity (rad/s) ≈ 261.799 rad/s

Therefore, the angular velocity for 2500 RPM is approximately 261.799 rad/s.

It’s important to note that angular velocity is a vector quantity, meaning it has both magnitude and direction. The direction of angular velocity depends on the direction of rotation. In this case, since we are only given the magnitude of the RPM, the direction of the angular velocity is not specified.

In addition to angular velocity, it is also common to consider other related quantities in rotational motion. These include rotational frequency (also known as angular frequency), rotational velocity, linear velocity, and tangential velocity. These quantities are interconnected through various motion equations and can be used to describe different aspects of circular motion and rotational kinematics.

So, whenever you need to convert RPM to angular velocity, remember to use the conversion factor of (2π/60) rad/s. This will allow you to accurately determine the angular velocity in rad/s for a given rotational speed in RPM.

Conclusion

In conclusion, understanding the concept of RPM (revolutions per minute) and angular velocity is crucial in various fields, including physics, engineering, and mechanics. RPM measures the number of complete rotations an object makes in one minute, while angular velocity measures the rate at which an object rotates in radians per second.

By converting RPM to angular velocity, we can determine the speed at which an object is rotating in a more precise and standardized unit. This conversion is done by multiplying the RPM value by 2π and dividing it by 60.

Having a clear understanding of RPM to angular velocity conversion allows us to analyze and calculate rotational motion accurately, making it an essential concept for anyone working with rotating objects or studying rotational dynamics.

How is angular velocity related to linear velocity?

Angular velocity and linear velocity are two concepts that are connected in the context of motion. Angular velocity refers to the rate at which an object rotates around a specific axis, while linear velocity represents the rate at which an object moves along a straight path. To understand the relationship between these two, it is important to explore how angular velocity is converted into linear velocity and vice versa. The article “Angular Velocity vs Linear Velocity: Explained” provides a detailed explanation of this connection and offers insights into the calculations and conversions involved.

Frequently Asked Questions

1. How do you calculate RPM from angular velocity?

To calculate RPM (Revolutions Per Minute) from angular velocity, you need to use the conversion factor. Angular velocity is typically measured in radians per second. To convert it to RPM, you divide the angular velocity by 2π (which is the radian equivalent of one revolution) and then multiply by 60 (to convert seconds to minutes).

2. Is RPM the same as angular velocity?

No, RPM and angular velocity are not the same, although they are related. RPM is a measure of how many times an object rotates around a circle in one minute, while angular velocity is a measure of the speed of rotation, typically expressed in radians per second.

3. What is the formula to convert RPM to angular velocity?

The formula to convert RPM to angular velocity is ω = RPM * 2π / 60, where ω is the angular velocity. This formula takes the RPM, multiplies it by 2π to convert revolutions to radians, and then divides by 60 to convert minutes to seconds.

4. How do you convert 20 RPM to angular velocity?

To convert 20 RPM to angular velocity, use the formula ω = RPM * 2π / 60. Substituting 20 for RPM gives ω = 20 * 2π / 60 = approximately 2.09 radians per second.

5. What is the relationship between angular velocity and RPM?

Angular velocity and RPM are both measures of rotational speed. They are related by the formula ω = RPM * 2π / 60, where ω is the angular velocity. This formula converts RPM to radians per second, which is the standard unit for angular velocity.

6. How do you convert 2500 RPM to angular velocity?

To convert 2500 RPM to angular velocity, use the formula ω = RPM * 2π / 60. Substituting 2500 for RPM gives ω = 2500 * 2π / 60 = approximately 261.8 radians per second.

7. Does angular velocity increase with radius?

No, angular velocity does not increase with radius. In circular motion, the angular velocity is independent of the radius. However, the linear or tangential velocity, which is the velocity of a point moving along the circumference, does increase with radius.

8. How do you convert RPM to angular velocity in radians per second?

To convert RPM to angular velocity in radians per second, use the formula ω = RPM * 2π / 60. This formula takes the RPM, multiplies it by 2π to convert revolutions to radians, and then divides by 60 to convert minutes to seconds.

9. How do you convert 400 RPM to angular velocity?

To convert 400 RPM to angular velocity, use the formula ω = RPM * 2π / 60. Substituting 400 for RPM gives ω = 400 * 2π / 60 = approximately 41.89 radians per second.

10. How do you find RPM given angular velocity?

To find RPM given angular velocity, you can use the formula RPM = ω * 60 / 2π, where ω is the angular velocity. This formula takes the angular velocity in radians per second, multiplies it by 60 to convert seconds to minutes, and then divides by 2π to convert radians to revolutions.

Also Read:

How To Find Angular Velocity:7 Scenarios With Solved Problem

November 3, 2023October 28, 2021 by Rabiya Khalid

Definition and Importance of Angular Velocity

angular velocity is defined as the rate of change of angular displacement with respect to time. It measures how quickly an object rotates and is typically denoted by the Greek letter omega (ω). angular velocity is an essential parameter in rotational dynamics, as it relates to other rotational quantities like angular acceleration, angular momentum, and moment of inertia.

Image by Svjo – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

Image by dnet – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

how to find angular velocity — Image by Svjo – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

angular velocity is an essential concept in physics and mechanics that describes the rate at which an object rotates around a fixed axis. Understanding angular velocity is crucial for various applications, such as analyzing the motion of rotating objects, calculating torque, or studying the behavior of pendulums. In this blog post, we will explore different methods and formulas to find angular velocity in various scenarios. So, let’s dive in!

Finding Angular Velocity from Frequency

A. Understanding the Relationship between Angular Velocity and Frequency

Frequency (f) represents the number of complete revolutions or cycles an object completes in a given time. The relationship between angular velocity (ω) and frequency is given by the formula:

$ω = 2πf$

B. Step-by-step Process to Determine Angular Velocity from Frequency

To find angular velocity from frequency, follow these steps:

Identify the frequency (f) of the rotating object.
Multiply the frequency by 2π to obtain the angular velocity (ω).

Examples:

Problem: A ceiling fan has blades that rotate at a speed of 120 revolutions per minute (rpm). Determine the angular velocity of the fan blades in radians per second (rad/s).

$\text{Step 1: Convert frequency from rpm to Hz.}$

$f (\text{in Hz}) = \frac{120 \text{ rpm}}{60 \text{ s/min}}$

$f = 2 \text{ Hz}$

$\text{Step 2: Calculate the angular velocity.}$

$\omega = 2\pi f$

$\omega = 2\pi \times 2 \text{ Hz}$

$\omega = 4\pi \text{ rad/s}$

$\text{Result:}$

$\text{The angular velocity of the ceiling fan blades is: }$

$\omega = 4\pi \text{ rad/s}$

$\text{For a numerical approximation:}$

$\omega \approx 4 \times 3.14159 \text{ rad/s}$

$\omega \approx 12.566 \text{ rad/s}$

$\text{Therefore, the fan blades have an angular velocity of approximately 12.566 radians per second.}$

Finding Angular Velocity Given Radius and Speed

A. The Role of Radius and Speed in Angular Velocity

When an object moves in a circular path, the distance traveled by a point on the object’s circumference in a given time is called linear speed (v). Angular velocity (ω) is related to linear speed and radius (r) by the formula:

$ω = \frac{v}{r}$

B. Detailed Procedure to Calculate Angular Velocity with Radius and Speed

To determine angular velocity using radius and speed, follow these steps:

Measure the radius (r) of the circular path.
Determine the linear speed (v) of the object.
Divide the linear speed by the radius to obtain the angular velocity.

Example:

Problem: A point on the edge of a merry-go-round is traveling at a linear speed (tangential speed) of 3 meters per second (m/s). If the radius of the merry-go-round is 2 meters, what is the angular velocity of the merry-go-round in radians per second (rad/s)?

$\text{Given:}$

$v = 3 \text{ m/s} \quad \text{(linear speed)}$

$r = 2 \text{ m} \quad \text{(radius)}$

$\text{The relationship between linear speed, angular velocity, and radius is:}$

$v = \omega r$

$\text{Solve for angular velocity:}$

$\omega = \frac{v}{r}$

$\omega = \frac{3 \text{ m/s}}{2 \text{ m}}$

$\omega = 1.5 \text{ rad/s}$

$\text{Therefore, the angular velocity of the merry-go-round is 1.5 radians per second.}$

Finding Angular Velocity from Linear Velocity

A. Connection between Linear Velocity and Angular Velocity

Linear velocity (v) refers to the rate at which an object moves along a straight path. The relationship between linear velocity and angular velocity is given by the formula:

$v = ωr$

B. Detailed Steps to Find Angular Velocity from Linear Velocity

To calculate angular velocity using linear velocity, follow these steps:

Measure the linear velocity (v) of the object.
Determine the radius (r) of the circular path.
Divide the linear velocity by the radius to obtain the angular velocity.

Example:

Problem: A bicycle tire has a diameter of 0.7 meters. The bicycle is moving at a linear speed of 5 meters per second along a path. What is the angular velocity of the tire in radians per second?

$\text{Given:}$

$d = 0.7 \text{ m} \quad \text{(diameter of the tire)}$

$v = 5 \text{ m/s} \quad \text{(linear speed)}$

$\text{The radius (r) is half of the diameter:}$

$r = \frac{d}{2} = \frac{0.7 \text{ m}}{2}$

$\text{The relationship between linear velocity, angular velocity, and radius is:}$

$v = \omega r$

$\text{Solve for angular velocity:}$

$\omega = \frac{v}{r} = \frac{5 \text{ m/s}}{\frac{0.7 \text{ m}}{2}}$

$\omega \approx \frac{5 \text{ m/s}}{0.35 \text{ m}}$

$\omega \approx 14.29 \text{ rad/s}$

$\text{Therefore, the angular velocity of the bicycle tire is approximately 14.29 radians per second.}$

Finding Angular Velocity from Torque and Moment of Inertia

A. Understanding Torque and Moment of Inertia in Angular Velocity

Torque (τ) is a rotational force that causes objects to rotate. The moment of inertia (I) represents an object’s resistance to changes in its rotational motion. Angular velocity can be found using torque and moment of inertia through the formula:

$τ = Iω$

B. Procedure to Determine Angular Velocity from Torque and Moment of Inertia

To find angular velocity using torque and moment of inertia, follow these steps:

Determine the torque (τ) acting on the object.
Identify the moment of inertia (I) of the object.
Divide the torque by the moment of inertia to obtain the angular velocity.

Example:

Problem: A disk with a moment of inertia of 0.2 kg·m² is initially at rest. A constant torque of 0.5 N·m is applied to the disk. After 4 seconds, what is the angular velocity of the disk?

$\text{Given:}$

$I = 0.2 \text{ kg}\cdot\text{m}^2 \quad (\text{moment of inertia})$

$\tau = 0.5 \text{ N}\cdot\text{m} \quad (\text{torque})$

$t = 4 \text{ s} \quad (\text{time})$

$\omega_0 = 0 \text{ rad/s} \quad (\text{initial angular velocity})$

$\text{Step 1: Calculate the angular acceleration:}$

$\alpha = \frac{\tau}{I}$

$\text{Step 2: Calculate the final angular velocity:}$

$\omega = \omega_0 + \alpha t$

$\text{Compute the values:}$

$\alpha = \frac{0.5}{0.2} = 2.5 \text{ rad/s}^2$

$\omega = 0 + 2.5 \times 4 = 10 \text{ rad/s}$

$\text{Therefore, the disk's angular velocity after 4 seconds is 10 rad/s.}$

Finding Angular Velocity in Specific Scenarios

A. How to Find Angular Velocity of a Rotating Object

To determine the angular velocity of a rotating object, follow the respective method discussed earlier based on the available parameters such as frequency, radius and speed, linear velocity, or torque and moment of inertia.

B. How to Find Angular Velocity in Simple Harmonic Motion

In simple harmonic motion, the angular velocity is related to the angular frequency (ω) by the equation:

$ω = \sqrt{\frac{k}{I}}$

where k represents the spring constant and I is the moment of inertia.

C. How to Find Angular Velocity of Earth

The angular velocity of the Earth can be calculated by dividing the Earth’s angular displacement by the time taken. However, it is important to note that the Earth’s angular velocity is very small, as it completes one full rotation in approximately 24 hours.

D. How to Find Angular Velocity of a Pendulum

For a simple pendulum, the angular velocity is given by the formula:

$ω = \sqrt{\frac{g}{L}}$

where g is the acceleration due to gravity and L represents the length of the pendulum.

Finding Angular Velocity without Certain Parameters

A. How to Find Angular Velocity without Time

If the time is not given, it is not possible to directly calculate angular velocity. However, if other parameters like angular displacement or frequency are provided, it may still be possible to determine the angular velocity using the relevant formulas.

B. How to Find Angular Velocity without Radius

When the radius of the circular path is unknown, it is not possible to find the angular velocity directly. However, if linear velocity or torque and moment of inertia are provided, it is still possible to calculate the angular velocity using the appropriate formulas.

15 Examples Of Angular Velocity

January 1, 2024October 24, 2021 by Rabiya Khalid

The angular velocity is the angular displacement per time of a body on an axis during circular motion or oscillation. Angular velocity examples in daily life are:

Ferris wheel
Race Car on the racetrack
Earth revolution
A rock tied with a rope and spinning around
Ceiling and Electric Fan
Simple Pendulum
Wheels
Hands of clock
Blades of Helicopter
The motion of electrons around the nucleus
Satellites orbiting around planets
Electric Beater
Washing Machine
Yo-Yo
Swing

Ferris wheel

The Ferris wheel moves in a circular motion. Due to the rotation, its angle changes and it attains angular velocity. Most of the time the angular velocity remains constant, that is it moves with uniform velocity but on the top and bottom position, the velocity gets accelerated. Due to the changes in velocity that leads to centripetal acceleration the rider feels heavy or light at the bottom and top position. Ferris Wheel is the basic example of an object moving in a circular motion with angular velocity.

Race Car on the racetrack

When a body moves on a straight path it has only a linear component of velocity. But if we take the example of a race car running on the race track then the angular velocity also comes into action. The racetracks are circular or they have curves. When the car turns on the track the angle changes with time and hence the car attains angular velocity.

Earth revolution

solar system 414388 1280 — Image Credit: https://cdn.pixabay.com/photo/2014/08/09/21/30/solar-system-414388_1280.jpg

The Earth and all the other planets revolve around the sun in a circular orbit. When they revolve their phase, that is angle keeps changing with respective time. This leads to the emergence of orbital angular velocity in Earth and heavenly bodies that revolve around the Sun. As planets go closer to the sun their angular velocity increases. This is due to an increase in gravitational pull and hence to maintain the angular momentum the angular velocity rises.

Rock tied with a rope and spinning around

When a rock tied with a rope or string is spun around, it orbits in a circular motion. Due to which the angle of the rock keeps changing concerning time. The angular displacement leads to the development of the angular velocity of the rock spinning around. This velocity is always direct along the axis of rotation. The centripetal force pushes the rock to gain angular velocity and allows their spinning. To gain maximum angular velocity a string with a shorter length is needed and vice versa. The angular momentum of the rock remains conserved at every point of the motion.

Ceiling and Electric Fan

air 2260 1280 — Image Credit: https://pixabay.com/photos/air-blade-blowing-chrome-cool-2260/

On switching the ceiling or electronic fans they start rotating. It spins in a circular motion and completes the cycles. The angular velocity of the fan is measured as the revolutions that it completes in a given time. The angular velocity of the fan changes by increasing and decreasing the speed. When the velocity changes the fan gets angular acceleration.

Simple Pendulum

The simple pendulum is a small bob hanging from a massless string. On striking the bob the pendulum starts oscillating from mean position to extreme points at both ends. While oscillating the pendulum keeps changing the phase which leads to the angular velocity. The angular velocity is the same concept as linear velocity, the difference is the type of motion. The angular velocity of the pendulum is never constant. When it reaches the endpoints the velocity tends to 0 but never becomes completely negligible. For pendulum one should be careful to not confuse the angular velocity with angular frequency.

Wheels

wheel rim 254714 1280 — Image Credit: https://pixabay.com/photos/wheel-rim-rim-of-wheel-wheel-tire-254714/

The rotation and motion of wheels is the most common example of angular velocity in everyday life. The wheels keep rotating on a fixed axis and keep changing the phase. The angular velocity is calculated by dividing the angle change with time. The angular component of the velocity of the wheel is also determined by specifying the revolution completed by the rotating wheel. The one revolution of the wheel is equal to 2π. Now suppose that the wheel completes 6 revolutions in one minute, then the angular speed would be 12π radians per minute.

Hands of clock

ezgif 7 63cb0ee3c003 — Image Credit: https://pixabay.com/photos/clock-alarm-alarm-clock-dial-time-1031503/

The minute hand and second hand of the clock keep rotating all day long at a fixed axis. Due to their rotation, their angle changes concerning time. Both of their velocities are different as they complete a different number of revolutions in a given time. It gives the idea about how fast the hands of the clock are moving.

Blades of Helicopter

helicopter 2116170 1280 — Image Credit: https://pixabay.com/illustrations/helicopter-rotors-aircraft-cockpit-2116170/

The blades of the helicopter start rotating as the engine starts. On rotation, the blades change the angle and complete the cycle. The number of cycles that it completes in a given time constitute the angular velocity of the helicopter. It is due to this velocity that the helicopter moves upward. The blades are rotated with an angular velocity which pushes the air downwards and uplifts the helicopter.

The motion of electrons around the nucleus

atom 1674878 1280 — Image Credit: https://pixabay.com/vectors/atom-chemistry-science-model-1674878/

In an atom, the negative subatomic particle i.e. electrons revolve around the nucleus in a uniform circular orbit. They move with angular speed which remains constant throughout the motion. Hence the electrons do not radiate energy while revolving. The angular component of the velocity of an electron is inversely proportional to its orbital number. The electrons which are nearer to the nucleus will have greater angular velocity rather than those farther from the nucleus. Along with the revolution, the electrons further spin on their own axis that also contributes to their angular velocity.

Satellites orbiting around planets

ezgif 7 3343473f356d — Image Credit: https://pixabay.com/photos/satellite-spacecraft-space-67718/

The motion of satellites around the planets is analogous to electrons’ revolution around the sun or we can say the other way around. The satellite orbits on a circular path around the planets to provide information about them. When they revolve there emerges angular velocity that helps in their motion. When the angular velocity of the satellite changes then the angular acceleration generates. To keep itself moving in orbit, the satellite speed remains near to constant.

Electric Beater

The electric beater is another device that has an angular component of velocity. When we switch on the beater its blade starts rotating on an axis. This rotation leads to the angular speed of the electric beater. Greater the angular speed greater would be the intensity with which the blade would move and faster the product would be whisked.

Washing Machine

The washing machine is another example of angular velocity. When the machine operates it spins and rotates on a fixed axis. The uniform circular motion brings the angular velocity into action. The centripetal force and the angular velocity contributes to the mechanism of the washing machine.

Yo-Yo

family 4978137 1280 — Image Credit: https://pixabay.com/vectors/family-adorable-kids-illustration-4978137/

Yo-yo is a simple toy that swings due to its angular velocity. When we throw the yo-yo it starts swinging and spinning to climb to the string. Its angular velocity keeps changing and hence it gets angularly accelerated.

Swing

The swings in the children’s park is also an example of angular velocity. It swings back and forth at continuous intervals. Moving ahead it makes an angle and with the same angle, it moves backwards. The change in angle leads to the emergence of the angular speed of the swing. Both the angular and linear velocity component helps in the swinging.

Angular Frequency vs Frequency: A Comprehensive Guide for Physics Students

June 26, 2024October 23, 2021 by Rabiya Khalid

Summary

Angular frequency and frequency are both measures of the rate of repetitive events, but they differ in their units and applications. Angular frequency, denoted by ω, is measured in radians per second (rad/s) and represents the rate of change of the phase angle of a periodic function. Frequency, denoted by f, is measured in cycles or oscillations per second (Hz) and represents the number of complete cycles or oscillations per unit time. The relationship between angular frequency and frequency is given by the equation ω = 2πf, which is crucial in understanding the dynamics of various physical systems.

Understanding Angular Frequency

Angular frequency, ω, is a fundamental concept in classical mechanics and wave mechanics. It represents the rate of change of the phase angle of a periodic function, such as an oscillation or a wave. The phase angle is the angle between the current position of the periodic function and its initial position.

Characteristics of Angular Frequency

Measured in radians per second (rad/s)
Represents the ‘speed’ or rate of change of a periodic function
Significant in understanding the dynamics of oscillating systems and wave propagation
Closely related to the period (T) of the periodic function through the equation ω = 2π/T

Calculating Angular Frequency

The angular frequency of a system can be calculated using various formulas, depending on the specific physical situation. Some common examples include:

Simple Harmonic Motion:
For a mass-spring system, the angular frequency is given by ω = √(k/m), where k is the spring constant and m is the mass.
Example: For a mass-spring system with k = 1.2 N/m and m = 0.4 kg, the angular frequency is ω = √(1.2/0.4) = 1.7 rad/s.
Electromagnetic Waves:
The angular frequency of an electromagnetic wave is used in the temporal part of the wave function, indicating the rate of change of the wave’s phase angle.
Example: The angular frequency of a radio wave with a frequency of 100 MHz is ω = 2πf = 2π × 100 × 10^6 = 6.28 × 10^8 rad/s.

Understanding Frequency

Frequency, f, is a measure of the number of complete cycles or oscillations per unit time. It is commonly used to describe the repetition rate of events, such as the number of times a pendulum swings per second or the number of cycles per second in an electrical signal.

Characteristics of Frequency

Measured in cycles or oscillations per second (Hz)
Represents the number of complete cycles or oscillations per unit time
Commonly used to describe the repetition rate of events
Closely related to the period (T) of the periodic function through the equation f = 1/T

Calculating Frequency

The frequency of a periodic function can be calculated using the following formula:

f = 1/T

Where T is the period of the periodic function, which represents the time taken for one complete cycle or oscillation.

Example:
– A pendulum oscillates with a period of 0.5 seconds.
– The frequency of the pendulum is f = 1/T = 1/0.5 = 2 Hz.

Relationship Between Angular Frequency and Frequency

The relationship between angular frequency and frequency is given by the equation:

ω = 2πf

This equation indicates that angular frequency is equal to 2π times the frequency. This means that if the frequency increases, the angular frequency also increases, and vice versa.

Numerical Examples

Pendulum Oscillation:
A pendulum oscillates at a frequency of 2 Hz.
The angular frequency of the pendulum is ω = 2πf = 2π × 2 = 4π rad/s.
Spring-Mass System:
A spring-mass system has a spring constant of 5 N/m and a mass of 20 kg.
The angular frequency of the system is ω = √(k/m) = √(5/20) = 0.5 rad/s.

Theorems and Physics Formulas

ω = 2πf (Relationship between angular frequency and frequency)
ω = √(k/m) (Angular frequency of a mass-spring system)
T = 1/f (Relationship between period and frequency)
ω = 2π/T (Relationship between angular frequency and period)

Figures and Data Points

Angular frequency is measured in radians per second (rad/s)
Frequency is measured in cycles or oscillations per second (Hz)
The period of an oscillation is the reciprocal of the frequency: T = 1/f
The angular frequency and period are related by: ω = 2π/T

Reference Links

https://www.vaia.com/en-us/explanations/physics/classical-mechanics/angular-frequency-and-period/
https://www.physicsforums.com/threads/the-difference-between-angular-frequency-and-frequency.938722/
https://www.quora.com/What-is-the-difference-between-angular-frequency-and-frequency-with-example