Riya Pandey - lambdageeks.com

Is Momentum Conserved In An Inelastic Collision: When, Why, How, Detailed Facts And FAQs

January 20, 2024December 21, 2021 by Riya Pandey

When two bodies physically strike each other, or if their path of motion is influenced by each other, then we say it as collision.

To know, Is Momentum Conserved In An Inelastic Collision, let’s first know collision. Collisions are of two types: an elastic collision and the other is an inelastic collision. When two bodies strike or collide, then the body’s kinetic energy is changed in the collision. Such a sort of collision is called an inelastic collision.

During any collision, the force exerted on the bodies when they two collide is equal and opposite at all instants during the collision. And when the collision gets over, the interacting force between them gets zero.

Is Momentum always conserved in inelastic collisions?

When two objects collide, either inelastic collision or in an inelastic collision, the collision between them is controlled by the law of Momentum and the law of energy.

Suppose the collision took place in an isolated system. We will find that the total Momentum of the bodies is conserved on the condition that the system of bodies does not experience any external force impacting it. Hence, the Momentum of the system’s body will be equal before and after the collision occurs.

During the collision, where two bodies are involved, we see that the Momentum loosed by one object is acquired by another object involved in the collision. As a consequence, the Momentum of the system of two bodies is intended to conserved.

Screenshot 260 — **Energy dissipated in deformation of body** Image credit: “HC03840” , Community Archives of Belleville & Hastings County, CC0 1.0

Why is Momentum conserved in an inelastic collision?

To understand “Why is Momentum conserved in an inelastic collision, let us go through the following. Let us take an example of a system having two object, in which the two objects strike to each other.

Wherein the two body are not bring to bear any sort of superficial force. The only force exerted by them is due to their interaction only. This means the two objects at any given instant have the same rate of Momentum change when they are interacting.

Hence, the objects in contact have equal and opposite Momentum. Because of this, the combined change in their Momentum will be zero. By the law of conservation of Momentum, we know that “In absence of any external force on the objects, the momentum of bodies will not be altered”. Now, Newton’s third law states that “the forces exerted by the objects interacting are equal and opposite”. And, the other condition is that objects must touch each other same span of time.

The given conditions are correct for all sorts of collisions where Newton’s third law is applied to all conditions where a force is applied. When these two conditions are met, the impulse delivered to each thing by the other is equal and opposite. Hence we can say that, As long as no external forces act on the system, Momentum remains conserved as a direct consequence of Newton’s second and third laws.

Where does Momentum go in an inelastic collision?

As above mentioned, during an inelastic collision, the Momentum gets preserved. Nonetheless, the kinetic energy of the system in the collision is not conserved.

The kinetic energy is not preserved because, it gets converted into other forms of energy when they strike to each other. For example, the object gets deformed, it changes into sound, heat, etc. To understand this, let’s take the instance of two trucks at outrageous velocities. The collision between the trucks here is inelastic.

Now, if we start to calculate the Momentum of the trucks, we will find that the Momentum of trucks before collision and Momentum after the collision when the trucks have collided is the same. But in the same place, if we calculated the kinetic energy of trucks when they were in speed and collided. Then the kinetic energy will be different. The kinetic energy of those trucks has been converted to some other form of energy.

is momentum conserved in an inelastic collision — **Energy dissipated in moving particle** Image credit: “Impact!”,☺ Lee J Haywood, CC BY-SA 2.0

Does the impulse-momentum theorem apply to inelastic collisions?

Impulse is the measure to which extent does an external force brings a change in the Momentum of the body.

We can also say that the Momentum of a body is the impulse required to bring a particle from rest to the motion. As we got to know that, the impulse is used to get an about the change in the state of moving particle, and we can use the impulse-momentum theorem in an inelastic collision.

Where impulse is given as:

J=ΔP

Is total Momentum conserved in an inelastic collision?

We can say that it is true that the total momentum of the body which are in an inelastic collision, have there total momentum conserved.

This can be observed, by calculating the sum of momentum of two bodies in inelastic collision. And calculating there momentum, once the collision has been occurred. The two calculation of before and after collision is found to be same.

Problems to explain Is Momentum conserved

Q. A gun which has a bullet of mass 100 gm. When the gun fires a bullet with a 75m/sec velocity. On firing the gun recoil with a velocity of 2m/sec. Now find the mass of the gun for the given condition.

By the law of conservation of Momentum

Mass of gun*recoil velocity of gun=mass of bullet*velocity of bullet

m₁v₁=m₂v₂

0.100*75=m₂*2

m₂=3.75kg

Q. Rajan is driving a truck loaded with goods, where its total mass is 200 kg. The truck is traveling in the the west direction with a 10m/sec speed. Now Rajan hits the rear end of a bus having a mass of 1400kg. After the collision, both truck and bus stick together. Now calculate the final Momentum of the vehicle after the collision.

We know that the formula for Momentum is given as Formula: Momentum P = MV.

From, law of conservation of momentum we get to know that,

P initial = P final

(MV)Truck+(MV) Bus = M_Truck+(M_Bus*Velocity)

(2000*10)(1400*0)=(2000+1400)*Velocity

20000/3400= Velocity

Velocity=5.8m/s

From the above-given calculation, we get to know that the vehicle will now move with a speed of 5.8m/s.

Q. Manan is moving down a steep hill, downwards. Manan has a mass of 20kg, and he is sliding down the slope at a 5m/sec velocity. Manan’s elder sister has a mass of 30 kg. Both of them are sliding down, but the sister is sloping slowly with a 2m/sec speed. Manan collides with her sister. After colliding, both of them start moving together. Now calculate their resultant velocity.

From the law of conservation of Momentum, we know that their collective Momentum will be equal to their final Momentum,

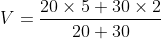
V=(100 kg.m/s+60 kg.m/s)/50 kg

V=3.20 m/sec

From the above calculation, we get that their combined velocity will be 3.20 m/sec.

Also Read:

Elastic vs inelastic collision

Is Momentum A Vector Quantity: Detailed Facts And FAQs

January 21, 2024December 14, 2021 by Riya Pandey

When a body has mass, it moves along a straight line. Then it is defined as its momentum.

Let us know, Is Momentum A Vector Quantity:- Newton’s second law of motion states that the rate of change of momentum of a body is directly proportional to the applied force, and this change takes place in the direction of the applied force.

From Newton’s second law, we understand that if a constant force is applied to a particle for a given period, the product of force and the time interval are equal to the change in the momentum. Contrariwise, the momentum of a body is defined as the time required to bring it to rest by a constant force.

Why is momentum a vector quantity

The product of mass and velocity, which is the momentum of a body, is a vector quantity because the direction of the body in motion will be in the direction same to the direction of the velocity of the body having mass. Where we know that quantities like displacement, position, velocity, force, and torque, these quantities have both magnitude and direction are vector quantities or vectors.

And we also know that quantities like mass, length, volume, Time, temperature, distance, and energy have magnitude only. They do not have directions are called scalar quantities or scalars.

Is linear momentum a vector quantity

Linear momentum is the product of mass, and the velocity of a body as its direction will be in the motion of velocity.

Linear momentum is a vector quantity, and it is represented by

Let us consider a body having mass and its velocity be then we get:-

Let us understand momentum and how it is a vector quantity:-

Suppose a bus has mass M1 and a truck has mass M2 (M2 greater than M1) in motion having the same velocities V moving in east. now their momentum will be P1 and P2, respectively.

So now we can write the equation as,

P₁/P₂=M₁V/M₂V=M₁/M₂

As we know, M2 is greater than m1, so P2 will be greater than P1. This means a body with a higher body mass will have large momentum than a body with light body mass.

Here the momentum is a vector quantity which means the bus and truck will move in the east direction.

Now lets us consider a bus of mass M1 and a truck of mass M2. Both are moving with the velocity of V1 in the east and V2 moving in the west, respectively, having the same linear momentum.

Now the equation can be written as:-

M1V1=M2V2

V₁/V₂=M₂/M₁

Here M2 is greater than M1, and V2 is greater than V1.

This means a heavier body has a smaller velocity, and a lighter body has a higher velocity.

Here we know momentum is the vector which means the bus will move in the east direction as its velocity directs, and the truck will move in the west direction as its velocity directs.

Is angular momentum a vector quantity

Angular momentum can be understood as the quantity corresponding to linear momentum in a rotational motion.

Let us understand angular momentum and whether it is a vector quantity:-

To understand angular momentum as a vector quantity, Let’s think about a particle with mass ”M,” And its linear momentum is given as, which it is at a position which is relative to the origin O.

Here the angular momentum of the particle will be:-

The angular momentum will also be vector quantity, whose direction will be decided through the right-hand screw rule.

The magnitude of angular momentum will be given as,

J=RPsinθ

Where is the angle between

We need to note that angular momentum will be 0 if the linear momentum is not there. Or, if the particle will be at the origin, which means R will be 0, or the directional line passes through the origin, the angular momentum will be 0.

From the above discussion, we got to know that angular momentum is a vector quantity. And from the right-hand screw rule, its direction is determined to be at right angles to the plane,

However, we need to note that the angular momentum of a particle or a system is due to the linear momentum transverse component. This means there is no contribution of the radial component.

Screenshot 255 — **Particle at position P**

Problems based on momentum

Q. Consider a toy train having a mass of 18 kg moving with a velocity of 8 m/s toward the south. What will be the momentum of the toy train?

We know that the momentum of the body will be:-

P=mv

Where m is 18 kg and v is 8 m/s

So the momentum of the toy train will be

P=18*8

=144kg.m/s

Q. There are Two trains of equal mass (2200 kg) that are moving at a speed of speed (72 km/h). The two trains collide head-on in a completely inelastic collision. Now, find out the vector sum of the momentum of the system of two trains after the collision?

The specified circumstance is an instance of an inelastic collision.

In these collisions, the kinetic energy will not get conserved (this means that it will be converted into some other form of energy, for example, heat energy ). However, the momentum will get conserved in any condition, whether it is an elastic collision or inelastic collision. And, as discussed above, momentum is a vector which means it has direction. Since the trains were of equal mass and traveled towards each other at the same speed as they collided, we know their momentum was equal in magnitude and opposite direction. This means the sum of their vector momentum before the collision will be 0.

Q.1-kg ball moves at speed of4 m/s. Now the ball is hit by an opposite force, F. This causes the speed of the ball to change to 12 m/s. The ball was in contact with the batsman for 0.02 seconds. Calculate the change in momentum of the ball.

From the above figures, we know that,

Mass of ball (m) = 1kg

Initial velocity (vo) = 4 m/s

Final velocity (vt) = -12 m/s

Time interval (t) = 0.02 second

Now to calculate the change, the given equation will be:-

∆p = m vt – m vo = m (vt – vo)

∆p = (1kg)(- 12 m/s – 4 m/s)

∆p = (1 kg)(-16)

∆p = 16kg m/s

Also Read:

How To Find Normal Force Between Two Blocks: Several Approaches and Problem Examples

January 21, 2024December 10, 2021 by Riya Pandey

How to Find Normal Force Between Two Blocks

When it comes to understanding the interaction between two blocks, the concept of normal force plays a crucial role. The normal force is the force exerted by a surface to support the weight of an object resting on it. In the case of two blocks in contact, the normal force is the force exerted by one block on the other perpendicular to the contact surface. In this blog post, we will explore how to find the normal force between two blocks, considering various factors such as friction, gravity, mass, and weight.

Identifying the Variables

Before diving into the calculations, let’s familiarize ourselves with the variables involved in finding the normal force between two blocks.

m1 and m2: The masses of the two blocks, respectively.
g: The acceleration due to gravity (approximately 9.8 m/s^2).
N: The normal force between the two blocks.
F_applied: Any externally applied force on the system.
F_friction: The force of friction between the blocks, if present.

Applying the Formula for Finding Normal Force

To calculate the normal force between two blocks, we need to consider the forces acting on the system. Newton’s second law of motion states that the sum of all forces acting on an object is equal to the mass of the object multiplied by its acceleration. In this case, we can apply Newton’s second law to the system of two blocks.

The formula for finding the normal force can be derived from Newton’s second law as follows:

$Sigma F = m_{text{total}} cdot a$

Here, $Sigma F$ represents the sum of all forces acting on the system, $m_{text{total}}$ is the total mass of the system $sum of the masses of the two blocks), and (a$ is the acceleration of the system.

Since we want to find the normal force between the two blocks, we can rearrange the equation to solve for $N$ :

$N = m_{text{total}} cdot a - F_{text{applied}} - F_{text{friction}}$

Worked Out Example: Calculating Normal Force

Let’s consider an example to illustrate how to calculate the normal force between two blocks. Suppose we have two blocks with masses of 2 kg and 3 kg, respectively, resting on a frictionless surface. An external force of 20 N is applied to the system.

To find the normal force, we can follow these steps:

Calculate the total mass of the system: $m_{text{total}} = m_1 + m_2 = 2 , text{kg} + 3 , text{kg} = 5 , text{kg}$ .
Determine the acceleration of the system: Since there is no friction or any other external force acting on the blocks horizontally, the acceleration is zero $(a = 0$ ).
Substitute the values into the formula to calculate the normal force: $N = 5 , text{kg} cdot 0 - 20 , text{N} - 0 = -20 , text{N}$ .

In this example, the negative value of the normal force indicates that the blocks are being pushed against each other, rather than being pulled apart.

Factors Affecting the Normal Force Between Two Blocks

Now that we know how to calculate the normal force, let’s explore the factors that can affect its magnitude.

The Role of Friction in Determining Normal Force

When there is friction between the two blocks, the force of friction affects the normal force. The force of friction opposes the relative motion between the blocks and depends on the coefficient of friction $(mu$ ) and the normal force itself. The formula for calculating the force of friction is:

$F_{text{friction}} = mu cdot N$

Where $mu$ is the coefficient of friction.

The Impact of Gravity on Normal Force

The gravitational force acting on each block contributes to the normal force between them. The weight of each block creates a downward force due to gravity. The formula for calculating weight is:

$text{Weight} = m cdot g$

Where $m$ is the mass of the block and $g$ is the acceleration due to gravity.

The Effect of Mass and Weight on Normal Force

The mass and weight of the blocks also affect the normal force between them. As the mass or weight of the blocks increases, the normal force also increases. This is because the weight of the blocks creates a downward force that must be balanced by the normal force.

Advanced Concepts Related to Normal Force

Let’s explore a few advanced concepts related to the normal force between two blocks.

Understanding the Normal Reaction Between Two Blocks

The normal force can also be referred to as the normal reaction. It is called a reaction because it is a force that acts in response to another force (in this case, the weight of the blocks). The normal force is always perpendicular to the contact surface between the blocks.

How to Calculate the Tension Between Two Blocks

In situations where the two blocks are connected by a rope or a string, it is possible to calculate the tension between them. The tension is the force transmitted through the rope or string and is equal in magnitude to the normal force between the blocks. By calculating the normal force, we can determine the tension in the rope or string.

Worked Out Example: Finding Contact Force Between Two Blocks Without Friction

Suppose we have two blocks with masses of 4 kg and 6 kg, respectively, resting on a frictionless surface. An external force of 30 N is applied to the system.

To find the contact force between the two blocks (which is equivalent to the normal force), we can follow these steps:

Calculate the total mass of the system: $m_{text{total}} = m_1 + m_2 = 4 , text{kg} + 6 , text{kg} = 10 , text{kg}$ .
Determine the acceleration of the system: Since there is no friction or any other external force acting on the blocks horizontally, the acceleration is zero $(a = 0$ ).
Substitute the values into the formula to calculate the normal force: $N = 10 , text{kg} cdot 0 - 30 , text{N} - 0 = -30 , text{N}$ .

In this example, the negative value of the normal force indicates that the blocks are being pushed against each other.

By understanding the concepts and formulas related to normal force, we can analyze and predict the behavior of blocks in various scenarios. Whether it’s calculating the normal force in a simple system or considering the impact of friction and gravity, mastering this concept is essential for understanding the physics of objects in motion.

Now that you have a solid understanding of how to find the normal force between two blocks, you can apply these concepts to a wide range of scenarios. Remember to consider factors such as friction, gravity, mass, and weight when calculating the normal force.

How does the concept of finding the normal force between two blocks relate to the idea of “Finding coefficient of kinetic friction”?

To understand how the concept of finding the normal force between two blocks intersects with the idea of “Finding coefficient of kinetic friction,” it is essential to consider the relationship between these two factors in a physics problem. The normal force is the perpendicular force exerted by a surface to support an object in contact, while the coefficient of kinetic friction represents the frictional force between two surfaces in relative motion. By determining the normal force, one can then calculate the coefficient of kinetic friction, as shown in the article “Finding coefficient of kinetic friction”. This article provides a comprehensive guide on how to calculate the coefficient of kinetic friction using various methods, which can be beneficial in scenarios where the normal force between two blocks is involved.

Numerical Problems on How to Find Normal Force Between Two Blocks

Problem 1:

Two blocks, A and B, are placed on top of each other on a horizontal surface. Block A has a mass of 5 kg and block B has a mass of 8 kg. The coefficient of friction between block A and the surface is 0.3, while the coefficient of friction between block B and block A is 0.2. Determine the normal force between the two blocks.

Solution:

Given:
– Mass of block A, $m_A = 5$ kg
– Mass of block B, $m_B = 8$ kg
– Coefficient of friction between block A and the surface, $mu_{A} = 0.3$
– Coefficient of friction between block B and block A, $mu_{B} = 0.2$

To find the normal force between the blocks, we need to consider the forces acting on each block individually.

For block A:
The weight of block A, $W_A = m_A cdot g$ , where $g$ is the acceleration due to gravity.
The normal force on block A, $N_A$ , is equal and opposite to the weight, so $N_A = W_A$ .
The friction force acting on block A, $F_{fA}$ , can be determined using the equation $F_{fA} = mu_{A} cdot N_A$ .

For block B:
The weight of block B, $W_B = m_B cdot g$ .
The friction force acting on block B, $F_{fB}$ , can be determined using the equation $F_{fB} = mu_{B} cdot N_A$ .

Since the two blocks are in contact with each other, the normal force acting on block B is equal to the friction force acting on block A, i.e., $N_B = F_{fA}$ .

Now, let’s calculate the normal force $N_A$ on block A:
$N_A = W_A = m_A cdot g$

Substituting the given values:
$N_A = 5 , text{kg} times 9.8 , text{m/s}^2$

Finally, we can calculate the normal force $N_B$ on block B:
$N_B = F_{fA} = mu_{A} cdot N_A$

Substituting the given values:
$N_B = 0.3 times N_A$

Calculating $N_B$ :
$N_B = 0.3 times (5 , text{kg} times 9.8 , text{m/s}^2)$

Hence, the normal force between the two blocks is $N_B$ .

Problem 2:

Two wooden blocks, P and Q, are placed on a table. Block P has a mass of 10 kg and block Q has a mass of 5 kg. The coefficient of friction between block P and the table is 0.4, while the coefficient of friction between block Q and the table is 0.3. Determine the normal force between the two blocks.

Solution:

Given:
– Mass of block P, $m_P = 10$ kg
– Mass of block Q, $m_Q = 5$ kg
– Coefficient of friction between block P and the table, $mu_{P} = 0.4$
– Coefficient of friction between block Q and the table, $mu_{Q} = 0.3$

To find the normal force between the blocks, we need to consider the forces acting on each block individually.

For block P:
The weight of block P, $W_P = m_P cdot g$ , where $g$ is the acceleration due to gravity.
The normal force on block P, $N_P$ , is equal and opposite to the weight, so $N_P = W_P$ .
The friction force acting on block P, $F_{fP}$ , can be determined using the equation $F_{fP} = mu_{P} cdot N_P$ .

For block Q:
The weight of block Q, $W_Q = m_Q cdot g$ .
The friction force acting on block Q, $F_{fQ}$ , can be determined using the equation $F_{fQ} = mu_{Q} cdot N_Q$ .

Since the two blocks are in contact with each other, the normal force acting on block Q is equal to the friction force acting on block P, i.e., $N_Q = F_{fP}$ .

Now, let’s calculate the normal force $N_P$ on block P:
$N_P = W_P = m_P cdot g$

Substituting the given values:
$N_P = 10 , text{kg} times 9.8 , text{m/s}^2$

Finally, we can calculate the normal force $N_Q$ on block Q:
$N_Q = F_{fP} = mu_{P} cdot N_P$

Substituting the given values:
$N_Q = 0.4 times N_P$

Calculating $N_Q$ :
$N_Q = 0.4 times (10 , text{kg} times 9.8 , text{m/s}^2)$

Hence, the normal force between the two blocks is $N_Q$ .

Problem 3:

Two blocks, X and Y, are connected by a string passing over a frictionless pulley. Block X has a mass of 6 kg and is on a horizontal surface, while block Y has a mass of 4 kg and is hanging vertically. Determine the normal force between the two blocks.

Solution:

Given:
– Mass of block X, $m_X = 6$ kg
– Mass of block Y, $m_Y = 4$ kg

To find the normal force between the blocks, we need to consider the forces acting on each block individually.

For block X:
The weight of block X, $W_X = m_X cdot g$ , where $g$ is the acceleration due to gravity.
The normal force on block X, $N_X$ , is equal and opposite to the weight, so $N_X = W_X$ .

For block Y:
The weight of block Y, $W_Y = m_Y cdot g$ .
The tension in the string, $T$ , is equal and opposite to the weight, so $T = W_Y$ .

Since the two blocks are connected, the normal force acting on block Y is equal to the tension in the string, i.e., $N_Y = T$ .

Now, let’s calculate the normal force $N_X$ on block X:
$N_X = W_X = m_X cdot g$

Substituting the given values:
$N_X = 6 , text{kg} times 9.8 , text{m/s}^2$

Finally, we can calculate the normal force $N_Y$ on block Y:
$N_Y = T = W_Y = m_Y cdot g$

Substituting the given values:
$N_Y = 4 , text{kg} times 9.8 , text{m/s}^2$

Hence, the normal force between the two blocks is $N_Y$ .

Also Read:

How To Find Tangential Force: Several Approaches And Problem Examples

January 21, 2024November 28, 2021 by Riya Pandey

Understanding tangential force is essential in various fields such as physics, engineering, and mechanics. tangential force refers to the force that acts tangentially to an object’s circular path. In this blog post, we will explore how to calculate tangential force, its relationship with tangential speed, its significance in gear mechanics, its association with radius and tension force, and its role in circular motion. Let’s dive in!

III. How to Calculate Tangential Force

A. The Formula for Calculating Tangential Force

The formula for calculating tangential force depends on the specific scenario. In general, tangential force can be calculated using the following formula:

$F_t = m \cdot a_t$

Where:
– (F_t) represents the tangential force
– (m) denotes the mass of the object
– (a_t) refers to the tangential acceleration

B. Step-by-Step Guide to Calculating Tangential Force

To calculate tangential force, follow these steps:

Determine the object’s mass (m).
Find the tangential acceleration (a_t) by using appropriate formulas for the given scenario.
Multiply the mass (m) by the tangential acceleration (a_t) to obtain the tangential force (F_t).

C. Worked Out Example: Calculating Tangential Force

Let’s consider an example to better understand the calculation of tangential force. Suppose we have a particle with a mass of 2 kg and a tangential acceleration of 3 m/s^2. To find the tangential force, we can use the formula:

$F_t = m \cdot a_t$

Substituting the given values, we get:

$F_t = 2 \, \text{kg} \cdot 3 \, \text{m/s}^2$

Simplifying the equation, we find that the tangential force (F_t) is equal to 6 N.

IV. The Interplay between Tangential Force and Tangential Speed

A. Understanding Tangential Speed

Before delving into the relationship between tangential force and tangential speed, let’s first understand tangential speed. tangential speed refers to the linear speed of an object moving in a circular path. It is measured in meters per second (m/s) and represents the rate at which the object covers the circumference of the circle.

B. How Tangential Force Influences Tangential Speed

tangential force has a significant impact on tangential speed. According to Newton’s second law of motion, the net force acting on an object is directly proportional to its acceleration. Therefore, the tangential force acting on an object influences its tangential acceleration, which, in turn, affects its tangential speed.

C. Worked Out Example: Finding Tangential Speed with Tangential Force

Suppose we have an object with a tangential force of 10 N and a mass of 5 kg. To find the tangential speed, we can use the formula:

$F_t = m \cdot a_t$

Rearranging the formula to solve for the tangential acceleration (a_t), we get:

$a_t = \frac{F_t}{m}$

Substituting the given values, we have:

$a_t = \frac{10 \, \text{N}}{5 \, \text{kg}}$

Simplifying the equation, we find that the tangential acceleration (a_t) is equal to 2 m/s^2.

Since tangential acceleration (a_t) is the rate at which the tangential speed changes, we can conclude that the object’s tangential speed will increase or decrease by 2 m/s in each second, depending on the direction of the force.

V. Tangential Force in Gear Mechanics

how to find tangential force — Image by Ilevanat – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

A. The Role of Tangential Force in Gear Operation

In gear mechanics, tangential force plays a crucial role in transmitting power and torque between gears. When two gears mesh, the tangential force acting on the teeth causes them to rotate and transfer rotational motion from one gear to another. The magnitude of the tangential force determines the effectiveness of power transmission and influences the gear system’s overall efficiency.

B. How to Calculate Tangential Force in Gear

To calculate tangential force in gear mechanics, follow these steps:

Determine the torque exerted on the gear.
Find the radius of the gear.
Use the formula (F_t = frac{T}{r}), where (F_t) represents the tangential force, (T) denotes the torque, and (r) refers to the radius.

C. Worked Out Example: Calculating Tangential Force in Gear

Let’s consider an example to illustrate the calculation of tangential force in gear mechanics. Suppose we have a gear with a torque of 50 Nm and a radius of 0.1 meters. To find the tangential force, we can use the formula:

$F_t = \frac{T}{r}$

Substituting the given values, we get:

$F_t = \frac{50 \, \text{Nm}}{0.1 \, \text{m}}$

Simplifying the equation, we find that the tangential force (F_t) is equal to 500 N.

VI. Tangential Force and Radius: A Crucial Relationship

How To Find Tangential Force: Several Approaches And Problem Examples 16

A. Does Tangential Velocity Change with Radius?

Yes, tangential velocity changes with radius. tangential velocity refers to the linear velocity of an object moving in a circular path. It depends on the object’s angular velocity and the radius of its circular path. As the radius increases, the tangential velocity also increases, assuming a constant angular velocity. Similarly, as the radius decreases, the tangential velocity decreases.

B. How to Find Tangential Velocity with Radius

To find the tangential velocity with radius, use the formula:

$v_t = \omega \cdot r$

Where:
– (v_t) represents the tangential velocity
– (omega) denotes the angular velocity
– (r) refers to the radius

C. Worked Out Example: Finding Tangential Velocity with Radius

Suppose we have a particle moving in a circular path with an angular velocity of 2 rad/s and a radius of 3 meters. To find the tangential velocity, we can use the formula:

$v_t = \omega \cdot r$

Substituting the given values, we get:

$v_t = 2 \, \text{rad/s} \cdot 3 \, \text{m}$

Simplifying the equation, we find that the tangential velocity (v_t) is equal to 6 m/s.

VII. Tangential Force and Tension Force: A Comparative Study

A. Understanding Tension Force

Tension force refers to the force exerted by a string, cable, or rope when it is pulled at both ends. It acts tangentially to the string’s length and is directed along the string. Tension force is responsible for transmitting forces and maintaining the equilibrium of objects connected by the string.

B. How to Calculate Tension Force

To calculate tension force, consider the forces acting on the object connected by the string. Use Newton’s second law of motion to set up equations based on the forces involved and solve for tension force.

C. Comparing Tangential Force and Tension Force

While tangential force acts tangentially to an object’s circular path, tension force acts along a string or cable. tangential force is responsible for the object’s circular motion, while tension force is responsible for transmitting forces through the string. Both forces play crucial roles in various scenarios and are essential for understanding different aspects of motion and equilibrium.

VIII. Tangential Force in Circular Motion: A Detailed Analysis

A. The Formula for Tangential Force in Circular Motion

The formula for tangential force in circular motion can be derived from the relationship between tangential force, mass, and tangential acceleration. It is given by the formula:

$F_t = m \cdot a_t$

B. How to Calculate Tangential Force in Circular Motion

To calculate tangential force in circular motion, follow these steps:

Determine the mass of the object (m).
Find the tangential acceleration (a_t) using appropriate formulas for circular motion.
Multiply the mass (m) by the tangential acceleration (a_t) to obtain the tangential force (F_t).

C. Worked Out Example: Calculating Tangential Force in Circular Motion

Let’s consider an example to illustrate the calculation of tangential force in circular motion. Suppose we have a car moving in a circular path with a mass of 1000 kg and a tangential acceleration of 5 m/s^2. To find the tangential force, we can use the formula:

$F_t = m \cdot a_t$

Substituting the given values, we get:

$F_t = 1000 \, \text{kg} \cdot 5 \, \text{m/s}^2$

Simplifying the equation, we find that the tangential force (F_t) is equal to 5000 N.

IX. Tangential Force and Tangential Distance: An In-depth Look

A. Understanding Tangential Distance

Tangential distance refers to the distance covered by an object along its circular path. It represents the length of the arc formed by the object’s circular motion. Tangential distance depends on the radius of the circular path and the angle subtended by the arc.

B. How to Calculate Tangential Distance

To calculate tangential distance, use the formula:

$d_t = r \cdot \theta$

Where:
– (d_t) represents the tangential distance
– (r) denotes the radius of the circular path
– (theta) refers to the angle subtended by the arc

C. Worked Out Example: Finding Tangential Distance with Tangential Force

Suppose we have an object moving along a circular path with a radius of 2 meters and an angle of 60 degrees. To find the tangential distance, we can use the formula:

$d_t = r \cdot \theta$

Substituting the given values, we get:

$d_t = 2 \, \text{m} \cdot 60^\circ$

Simplifying the equation, we find that the tangential distance (d_t) is equal to 120 meters.

Also Read:

Can Normal Force Be At An Angle: Several Approaches And Problem Examples

January 21, 2024November 25, 2021 by Riya Pandey

When two bodies come in contact -surfaces, a component acts upon them perpendicular to the contact surface. This is known as normal force.

Can normal force be at an angle:- The normal force exerted on the body tends to balance the gravity force (mg) on the body. As the normal force depends upon the value of force experienced by a body, but the normal force is always perpendicular to the body.

We need to understand the force exerted on a body. Let us take an example of a block that is at rest position on the table surface.

Screenshot 235 — **A block at rest position on a table**

In this condition, the block experiences two types of forces.

First is the gravity force (mg) which acts vertically downwards at the center of gravity of the block.
Second is the reactionary force P which acts vertically upward. These forces are passing through the center of gravity of the block.

Hence the block is in P= mg.

Now, if we apply any external force F on the block, suppose in the right direction. In this condition, the block does not move. Instead, the force P ( vertically upward) is now inclined in the left direction. Here the force P acting on the block can be divided into two components. One will be parallel, and the other will be perpendicular to the contact surface.

can normal force be at an angle — **Normal force acting at perpendicular**

Force of static friction this force balance the applied force F . in contrast, the force which is perpendicular to the block is known as normal force R . (R=mg).

The limiting frictional force is directly proportional to the normal force:-

f_sαR

The coefficient of limiting friction is the ratio of limiting frictional force to the normal force.

When two surfaces are in relative motion, the force acting between them is known as kinetic frictional force fk. This is less than the limiting fraction, this is given as:-

fk=μkR

Where ,

μk<μs

To check whether “can normal force be at an angle” lets check it through the following conditions:-

While pulling roller:-

When a roller of mass m is tried to pull over a horizontal surface by applying a force of F at an angle . As shown below in the figure:-

Screenshot 237 — **Pulling of a roller**

By considering that roller is in equilibrium, we say that:-

R₁+Fcosθ=mg

R₁=mg-Fcosθ

Here the coefficient of static friction between roller and surface is, then we can write f_s as:-

f_s=μ_sR1

f_s=μ_s(mg-Fcosθ)

Now we can say that normal force is perpendicular to the center of gravity of the roller.

When a roller of mass m is tried to push over a horizontal surface by applying a force of F at an angle. As shown below in the figure:-

Screenshot 238 — **Pushing of a roller**

R2=Fcosθ+mg

f_s‘=μ_sR2

f_s‘=μ_s(Fcosθ+mg)

In this condition also the normal force is perpendicular to the center of gravity of the roller.

From the given an example, while comparing Equations 1 and 2, we can say that it is easier to pull a roller rather than to push it because frictional force is less while pulling.

If we consider a case of rolling friction which is much less than sliding friction, in this case, also we find normal force at 90 degrees only.

As we know, the rolling friction is directly proportional to the normal force R. and inversely proportional to the radius r of the wheel.

f_rαR/r

f_r=μ_r*(R/r)

Where μ_r is the coefficient of rolling friction.

From all the given examples, we know that normal force is always perpendicularly upward to the center of gravity of the body.

Problem examples related to normal force:-

A force of 980N is just able to move a block of having a mass of 200kg on a rough horizontal; surface. Calculate the coefficient of friction and the angle of friction?

The force of 980 N is equal to the limiting frictional force. Hence the coefficient of static friction is:

μ_s=f_s/R

Where R is the normal force is equal to mg.

μ_s=980/(200*9.8)

μ_s=0.05

The angle of friction is given by;

tan θ_s=μ_s=0.05

θ_s=tan^-1(0.05)

A block of mass 2kg is placed on the floor. The coefficient of static friction is 0.4. A force of 2.5 N is applied on the block, as shown. Calculate the force of friction between the block and the floor?

Let R be the normal force on the block exerted by the floor. The limiting force of static friction is:

f_s=μ_rR=μ_smg

0.4*2kg*9.8ms²

7.84N

When a weight of a body placed on a surface is doubled, how does the coefficient of friction change?

There is No change in the coefficient of friction. In fact, the force of the limiting fraction is doubled.

f_s=μ_sR=μ_smg

Explain how lubricating can help in reducing friction?

When we lubricate a body, then the lubricant form a thin layer around two surface. In such condition the sliding friction is replaces by liquid friction. Where liquid friction is less than sliding friction. this results in less friction.

Can we jump off from a frictionless horizontal surface?

No, we can not jump off from a frictionless horizontal surface. Because a frictionless surface does not offer, normal reaction.

What are the conditions on which the coefficient of friction between two surfaces depends?

The coefficient of friction depends upon the nature of both surfaces in contact, its evenness and the surface temperature.

Also Read:

Periodic Motion Vs Simple Harmonic Motion: Detailed Explanation

January 21, 2024November 19, 2021 by Riya Pandey

A body is acknowledged to be in motion if it changes its position with respect to its encompassing in a given time.

Periodic motion vs simple harmonic motion can be explained as, A body is said to be in periodic motion if it continuously Repeats its motion on a particular path in a certain period of time. While on the contrary, simple harmonic motion can be acknowledged as the simplest form of vibratory or oscillatory motion.

Periodic Motion

Periodic motion can be understood by motion which we observe on a daily basis. In periodic motion, it is not necessary that the displacement that occurred in the body is in the direction of the restoring force.

For instance, the earth completes its one rotation on its own axis in 1 day. The motion of the moon is also a periodic motion as we know that the moon completes one revolution around the earth in approx. 27 days.

Similarly, the motion of hands in our clock is also a periodic motion. These all motions keep on repeating themselves in a particular path and in a certain period of time.

Simple Harmonic Motion

Simple harmonic motion can be understood as the periodic motion oneself because simple harmonic motion is a type of oscillatory motion. Where a vibratory motion or oscillatory motion is assumed as a body, which is performing periodic motion and moves along the definite path back and forth about a definite position (fixed position), then the motion of the body is known as ‘vibratory motion’ or ‘oscillatory motion.’

Screenshot 222 — vibratory or oscillatory motion

In the above-given figure, we can see that that the body is moving back and forth from the fixed position. Here the body oscillates from the fixed point O to the other side, covering maximum displacement to A, and then comes back to position fixed position O and then goes to another side A’ covering maximum displacement. From point A’ body comes forth to fixed point O again. this back and forth motion done by a body is said to complete ‘1 vibration’ or ‘1 oscillation’.

However, it is proved that each oscillatory motion is automatically a periodic motion, but each periodic motion is not a vibratory or oscillatory motion. For instance, the earth rotates on its own axis but does not move back and forth about a certain point along a path (this is an essential condition for an oscillatory motion that is not followed in the given case.).

Simple harmonic motion has a sine wave waveform of amplitude vs time.

Screenshot 224 — time displacement curve of a body performing SHM

In the above-given figure, the time-displacement curve of a body oscillating back and forth about its fixed position is shown. The displacement y is measured from the fixed position, and the time t is measured from the point when the body passes through its fixed position. One oscillation is completed from point O to point A, and the time T taken for one oscillation is the periodic time of the body.

The maximum value of displacement y in the given figure will be a. this maximum displacement is known as amplitude. The total number of oscillations that a body performs in a time period of 1 second is known as frequency. The frequency (n)is the reciprocal of the time period.

When a body vibrates, its position and direction of motion vary with time. The phase of a vibrating body at any point of time shows the motion of the body at that point of time. At any point in time, two vibrating bodies are passing simultaneously through their equilibrium positions in the same direction, then at that instant, they are in the same phase, and if they are passing in opposite directions, then they are in opposite directions.

Irrespective of periodic motion, Simple harmonic motion needs certain conditions to be satisfied:-

For simple harmonic motion, the body should be in a straight line moving back and forth about a fixed position
The restoring force acting on the body should always be proportional to the displacement of the body from the point.

Restoring force is when a body takes the place of its stable position. Now a recurrent force acts upon it, which is directed towards the stable position. It is due to this force that acceleration is produced in the body, and it starts vibrating back and forth

This force is given by :

F= -kx

when restoring force is proportional to the dislocation of the body from the stable position, then the rate of change of velocity of the body is also proportional to the dislocation of the body, and it vibrates, performing the simple harmonic motion.

Where k is force constant and x is displacement and – sign indicates that the body is displaced in the opposite direction.

The force should always be directed towards the fixed point.

Simple harmonic motion can be explained through the following examples. A body attached to a spring in a horizontal plane produces vibrations which are simple harmonic in nature, oscillations by a simple pendulum, the motion of a body dropped in an imaginary tunnel across the earth, oscillations of a body floating in liquid, newton cradle, swings, oscillation of a body in the neck of an air chamber.

We can conclude the difference between periodic motion vs simple harmonic motion on the basis of restoring force that acts on the body performing oscillations which are supposed to be proportionate to the dislocation of the body, whereas periodic motion repeats itself continuously without any given conditions.

Frequently Asked Questions

Two conditions are given as follow:-

General vibration of a polyatomic molecule about its configuration is such a case. they have different natural frequencies and due to this its oscillation there is a superposition of SHM of a number of variable frequencies. this superposition is periodic but not SHM.

Revolution of the earth around sun is periodic but it is not a SHM.

Frequency and time period of a particle performing SHM are related as-

Frequency is reciprocal of time period.

Also Read:

Simple Harmonic Examples: Detailed Explanation

January 21, 2024November 1, 2021 by Riya Pandey

When a particle moves in a straight line to and fro about its equilibrium position, then the particle’s motion is called ‘simple harmonic motion. let discuss simple harmonic motion examples.

A Clock Pendulum
Oscillation of guitar strings
Car Suspension
Hearing
Bungee Jumping
Swing
Newton’s Cradle
Motion of a body in a hole drilled through the center of the earth
Mass loaded on springs
Oscillation of block in liquid
Torsion pendulum
Oscillation of a ball in an air chamber

A Clock Pendulum

When a point mass has a weightless, inextensible, and perfectly flexible string that is suspended from rigid support, then such an arrangement is known as a simple pendulum. If we slightly displace the point mass to one side and release it. Then in such circumstances, the simple pendulum starts swinging, to and fro from its mean position. This swinging of a simple pendulum in a straight line from its mean position is an example of simple harmonic motion.

Oscillation of guitar strings

A musical instrument like guitar strings is an example of simple harmonic motion. When we twang a guitar string, The string starts moving to and fro. First, strings of guitar move forward and then move in the opposite direction. This motion causes vibration. These vibration created by guitar strings creates sound waves that human ears hear as music

Car Suspension

A car suspension system contains springs, as the springs have elasticity property whenever there is any bump the spring compresses which results in rising of cars wheels without actual rising the car body similarly when springs expand it causes the wheel to drop without the actual dropping of car body this causes to and fro motion which is Simple harmonic motion. Although this type of motion is damping which means it reduces over a period of time. This simple harmonic motion reduces the shock which passengers receive when a car goes across a bump.

Hearing

It is due to Simple harmonic motion that living organism has the ability to hear. When the vibrating molecules come upon our eardrums, it causes our eardrums to wobble. These vibrations caused in our eardrums are passed to organisms’ brains. In due course, these details are transmitted to the organism’s brain through auditory nerves, the brain then translates these vibrations into apprehensible sounds.

Bungee Jumping

Simple harmonic motion examples can also be seen in our sports, for example, bungee jumping. In an adventurous sport like bungee jumping, a long recoiling cable is tied up to the person’s legs. Then person performs bungee jumping jumps from a particular platform situated at height.

When the person jumps off the cliff, due to the recoiling cable, he is pulled back and again moves down due to gravity; this keeps ongoing. As a repetitive to and fro motion can be seen in bungee jumping, it is an example of simple harmonic motion.

Swing

Swings can easily be seen in amusement parks, gardens, schools, etc. The motion shown in swings is known as simple harmonic motion because while swinging, the child sitting on it experiences the force acting upon it, which is directly proportional to its displacement and directed towards the equilibrium position. This causes the back and forth, repetitive motion of the swing, causing simple harmonic motion.

Newton’s Cradle

Simple harmonic motion can be seen in Newton’s cradle. This is an apparatus that shows the principle of conservation of momentum and the principle of conservation of energy.

Newtons cradle consists of 5 metal balls suspended by string so that the movement of spheres is in one place. All balls are placed so that all orbs are at rest and all balls are in contact with the adjacent ball. In newtons cradle, when the endmost sphere is taken from rest and pulled and released, the sphere starts swinging like a pendulum, and the released sphere hits the adjacent ball.

When the adjoining sphere comes in contact with the released sphere, the energy and momentum from the released ball are transmitted through the three balls at rest to the final ball on the other endmost sphere. The transfer of energy and momentum causes the ball to be in motion with the same speed as the first ball. If more than one sphere is pulled up and released, then the same number of balls, as much released, will be set in motion from the end of the resting spheres. Here we can see oscillation of the balls ( to and fro). They are showing simple harmonic motion.

Motion of a body in a hole drilled through the center of the earth

Imagine if we have a tunnel through the earth’s center and a body having some mass released inside it. Then due to gravitational attraction, force, which acts upon the body, moves towards the earth’s center. Here the body will never fall to another side of the hole of the earth due to variation in the gravitation constant ‘g, which is maximum at the surface and zero at the center of the earth.

When the body falls toward the center of the earth, it only reaches the center, then again gravitational pull is exerted on it due to which moves back again in the opposite direction. This process keeps ongoing. This periodic motion of the body inside the earth hole is a simple harmonic motion. However, this is a theoretical example of Simple harmonic motion.

Mass loaded on springs

when a mass is suspended from the lower end of the springs, then due to its weight, the length of the spring is increased. Due to the elasticity of springs, it exerts a restoring force, due to which its moves again in the opposite direction. When we pull, the mass is suspended slightly downward and released. Then it oscillates up and down along with loaded mass, which is an example of Simple harmonic motion.

Oscillation of block in liquid

Oscillation of block in liquid is also an example of simple harmonic motion. When the block is pushed down a little into the liquid and left, it begins to oscillate up and down in the liquid showing simple harmonic motion.

simple harmonic motion examples — Oscillation of block in liquid

Torsion pendulum

The torsion pendulum is an example of angular simple harmonic motion. A torsion pendulum consists of a disc that is suspended by a thin wire. When it is twisted and released, it moves back and forth direction executing simple harmonic motion. A torsion pendulum rotates in place of the swing. Such types of pendulums are used in a mechanical wristwatch.

Screenshot 217 — torsional pendulum showcasing SHM

Oscillation of a ball in an air chamber

A ball in an air chamber having a long neck also shows simple harmonic motion. Suppose we consider a ball in the neck of an air chamber having air pressure in it. The air pressure in the container is atmospheric. If we slightly push down the ball in the neck of the air chamber, the ball will start oscillating up and down, showing simple harmonic motion.

Screenshot 206 — oscillation of a ball in an air chamber showing SHM

Also Read: