Angular momentum is a fundamental concept in physics that describes the rotational motion of an object. It plays a crucial role in various areas, from understanding the movement of planets to analyzing the behavior of spinning tops. To calculate angular momentum, we need to consider several factors, one of which is mass. In this blog post, we will explore how to find angular momentum with mass, understand the underlying principles, and provide examples to solidify our understanding.
How to Calculate Angular Momentum
The Role of Mass in Calculating Angular Momentum
Mass is a critical factor in determining an object’s angular momentum. It represents the amount of matter an object contains and is measured in kilograms (kg). The distribution of mass around an axis of rotation affects how the object spins and, consequently, its angular momentum.
The Formula for Angular Momentum
The formula for angular momentum is given by:
![]()
Where:
– ![]() is the angular momentum,
is the angular momentum,
– ![]() is the moment of inertia, and
is the moment of inertia, and
– ![]() is the angular velocity.
is the angular velocity.
Worked Out Example: Calculating Angular Momentum with Given Mass
Let’s consider an object with a mass of 2 kg rotating about a fixed axis. The moment of inertia of the object is 5 kg·m², and its angular velocity is 3 rad/s. To calculate its angular momentum, we can use the formula:
![]()
Substituting the given values, we have:
![]()
Calculating the product, we find:
![]()
Therefore, the angular momentum of the object is 15 kg·m²/s.
Factors Influencing Angular Momentum
The Impact of Torque on Angular Momentum
Torque, represented by the symbol ![]() , is the rotational equivalent of force. It is responsible for changing an object’s angular momentum. When a torque is applied to an object, it causes it to accelerate or decelerate its rotation, altering its angular momentum.
, is the rotational equivalent of force. It is responsible for changing an object’s angular momentum. When a torque is applied to an object, it causes it to accelerate or decelerate its rotation, altering its angular momentum.
The Role of Velocity in Determining Angular Momentum

Angular velocity, denoted as ![]() , is another crucial factor in calculating angular momentum. It represents the rate at which an object rotates around an axis and is measured in radians per second (rad/s). The faster an object rotates, the higher its angular velocity, resulting in a greater angular momentum.
, is another crucial factor in calculating angular momentum. It represents the rate at which an object rotates around an axis and is measured in radians per second (rad/s). The faster an object rotates, the higher its angular velocity, resulting in a greater angular momentum.
The Effect of Moment of Inertia on Angular Momentum

The moment of inertia, denoted as ![]() , quantifies an object’s resistance to changes in its rotational motion. It depends on the object’s mass distribution and the axis of rotation. Objects with a greater moment of inertia require more torque to change their angular momentum compared to objects with a smaller moment of inertia.
, quantifies an object’s resistance to changes in its rotational motion. It depends on the object’s mass distribution and the axis of rotation. Objects with a greater moment of inertia require more torque to change their angular momentum compared to objects with a smaller moment of inertia.
Advanced Concepts in Angular Momentum
Angular Momentum of a System
When multiple objects are involved in a rotational system, the total angular momentum of the system can be calculated by summing the individual angular momenta of each object. This principle applies to both isolated systems and systems influenced by external torques.
Angular Momentum without Mass: Theoretical Perspective
In certain cases, the concept of angular momentum can be extended beyond objects with mass. For example, in quantum mechanics, particles without any physical size, such as photons, can possess angular momentum. This highlights the versatility and broad applicability of the concept of angular momentum.
Angular Momentum and Center of Mass
The center of mass of an object plays a significant role in determining its angular momentum. When an object rotates about its center of mass, the calculation of angular momentum becomes simpler. The distance between the axis of rotation and the center of mass directly affects the object’s moment of inertia and, consequently, its angular momentum.
Understanding how to find angular momentum with mass is crucial for comprehending the rotational behavior of objects. By considering factors such as mass, torque, velocity, and moment of inertia, we can accurately calculate and analyze angular momentum. This knowledge allows us to explore various physical phenomena, ranging from celestial movements to everyday spinning objects, providing us with a deeper understanding of the world around us.
Numerical Problems on how to find angular momentum with mass
Problem 1:

A particle of mass ![]() is moving in a circular path with a radius
is moving in a circular path with a radius ![]() at a constant speed
at a constant speed ![]() . Find the angular momentum of the particle.
. Find the angular momentum of the particle.
Solution:
The angular momentum ![]() ) of a particle is given by the formula:
) of a particle is given by the formula:
![]()
Substituting the given values, we have:
![]()
![]()
Therefore, the angular momentum of the particle is ![]() .
.
Problem 2:
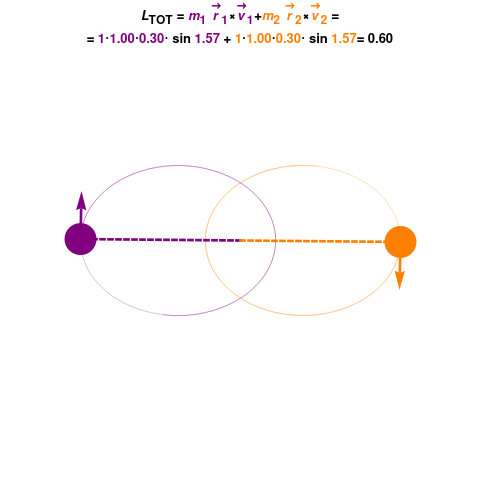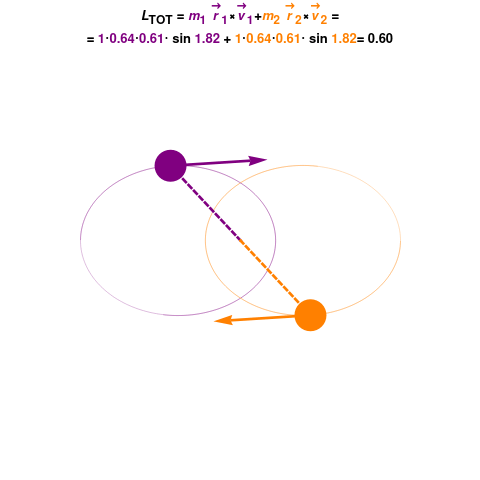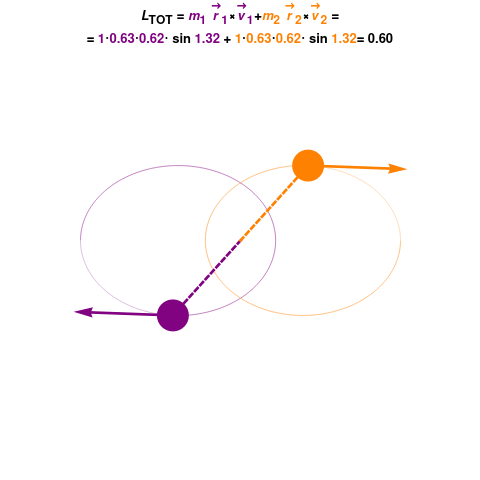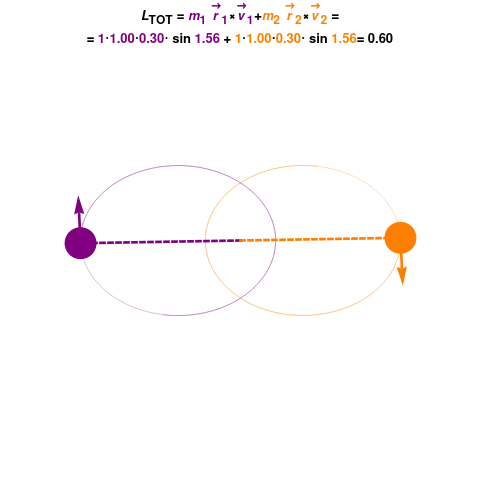
A particle of mass ![]() is moving in a circular path with a radius
is moving in a circular path with a radius ![]() at a constant speed
at a constant speed ![]() . Find the angular momentum of the particle.
. Find the angular momentum of the particle.
Solution:
Using the same formula as in Problem 1, we can calculate the angular momentum ![]() ) as follows:
) as follows:
![]()
Substituting the given values, we have:
![]()
![]()
Therefore, the angular momentum of the particle is ![]() .
.
Problem 3:
A particle of mass ![]() is moving in a circular path with a radius
is moving in a circular path with a radius ![]() at a constant speed
at a constant speed ![]() . Find the angular momentum of the particle.
. Find the angular momentum of the particle.
Solution:
Again, using the same formula as in the previous problems, we can find the angular momentum ![]() ) as follows:
) as follows:
![]()
Substituting the given values, we get:
![]()
![]()
Therefore, the angular momentum of the particle is ![]() .
.
Also Read:
- How to find relativistic momentum
- How to find momentum in fluid dynamics
- How to find angular momentum of a system
- How to find final momentum after collision
- How to find momentum for a photon
- What is change in momentum
- Is momentum conserved
- How to find conservation of momentum
- How to find momentum from kinetic energy
- Law of conservation of momentum
Hi ….I am Abhishek Khambhata, have pursued B. Tech in Mechanical Engineering. Throughout four years of my engineering, I have designed and flown unmanned aerial vehicles. My forte is fluid mechanics and thermal engineering. My fourth-year project was based on the performance enhancement of unmanned aerial vehicles using solar technology. I would like to connect with like-minded people.

Hi Fellow Reader,
We're a small team at Techiescience, working hard among the big players. If you like what you see, please share our content on social media. Your support makes a big difference. Thank you!