Electronics

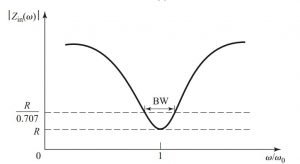
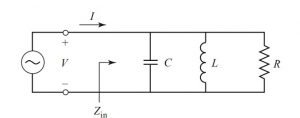
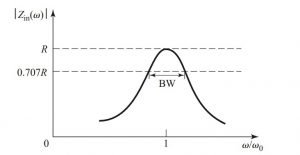
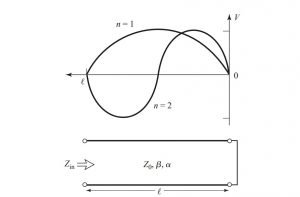
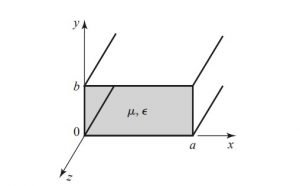
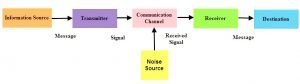
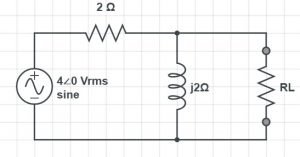
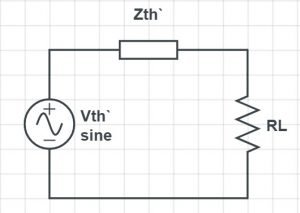
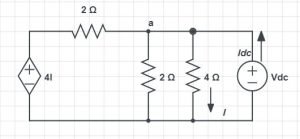
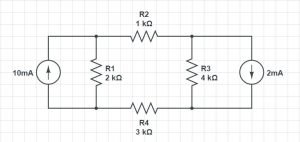
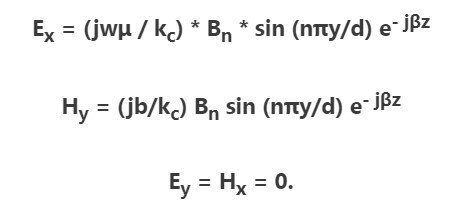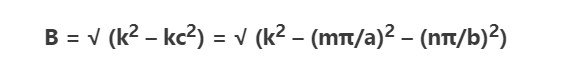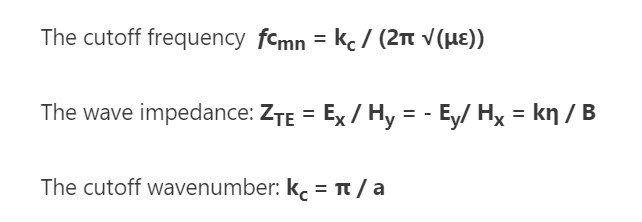Definition of a wattmeter:      

A wattmeter is made of a current coil that carries the load current and a voltage coil or pressure coil. These coils carry a current proportional to it and in phase with the voltage as shown in the figure.

Voltage coil is often referred as pressure coil. Inductance in Voltage coil, current is minimized as it causes the Voltage coil current to lag behind the applied voltage. To overcome this, a non-inductive resistance is connected in series with the voltage coil as shown in the figure above.

Working Principle of an Electrodynamic Wattmeter:

A PMMC (permanent magnet moving coil) instrument cannot be used on ac currents or voltages.

To produce an alternating torque, a supply is given to these instruments. But due to the presence of moment of inertia in the moving system, the pointer unable to make this rapid change and it will not display that reading. For this, the magnetic field in the gap must change along with the change of current so instrument is capable to read ac signal. This principle is used in these instruments only the operating field is provided by current carrying coils instead of magnets.

The moving coil carries a current proportional to the supply voltage. It is connected across the supply hence also called voltage coil or pressure coil. The fixed coil is connected in series with the load and carries current proportional to the load. Fixed coil is also called current coil. When fixed coil carries current, it produces its own flux and when current carrying moving coil is placed in this flux, it experiences a force, generating the required deflecting torque to deflect the pointer.

DC OPERATION:

V = supply voltage

I₁ = load current = current through fixed coil

I₂ = current through moving coil

Now, I₂ α V

The fixed coil is air cored hence flux density produced in the coil is directly proportional to the current through the coil.

Hence, B α I₁

Now the deflecting torque is proportional to the interaction of two quantities i.e., flux produced by fixed coil and current through the moving coil.

T_d α BI₂

T_d α I₁I₂

T_d α VI­₁

But V₁ is power consumed by load hence deflecting torque is proportional to the power consumed by the load.

AC OPERATION:

Let e = instantaneous voltage across load

            = E_m sin (ωt -Ø)

i₁ = instantaneous load current

    = current through fixed coil

If load is inductive in nature,

i₁ = I_m sin(ωt – Ø)

i₂ = instantaneous current through moving coil

V = r.m.s value of voltage across load

I₁ = r.m.s value of load current

cosØ = power factor of load

the deflecting torque is proportional to interaction of two fluxes; one produced by current i₁ and other by i₂

T_d α i₁i₂

But i₂ α e as moving coil is across the supply

T_d α ei

             α   E_m sinωt x I_m sin (ωt – Ø)

             α   ½ E_mI_m [cos (Ø) – cos (2ωt – Ø)]

            α          ½ E_mI_m cos (Ø) – ½ E_mI_m cos (2ωt – Ø)

hence the average torque is

T_d α ½ E_mI_m cosØ

             α          .  . cosØ

T_d α VI cos (Ø) where V and I₁ are r.m.s values. But VI₁cos(Ø) is power consumed by the load. Thus the deflecting torque is directly proportional to the power consumed by load.

T_c α θ as spring control

In steady state, T_d = T_c

                             Θ α VIcos(Ø)

Dynamometer type Wattmeter vs induction type Wattmeter:

Dynamometer type Wattmeter	Induction type Wattmeter
This type of wattmeter can be used on both ac and dc system In carefully designed instruments, it provides high degree of accuracy. This wattmeter has less power consumption criteria. Weight of moving system in this system is reasonably low This is in uniform scale. It has relatively weaker working torque.	The type of wattmeter can only be used on ac system. The instrument is less accurate. It is accurate only at stated frequency and temperature This induction type wattmeter has higher power-consumption requirements. Weight of moving system in this system is reasonably higher It has linear scale The instrument has comparatively stronger working torque

Explain the working principle of a moving iron instrument:

Most commonly used laboratory ammeters and wattmeter are of moving iron type, there are two types of moving iron instruments-

a. Moving iron attraction type instruments.

b. Moving iron repulsion type instruments

 Moving iron attraction type instruments-

This is having a fixed coil C and an iron piece D. The coil structure is flat and it has a narrow slot type of opening.

It’s a flat disc type, which is mounted eccentrically arranged at the spindle and spindle is in-between the jewel bearing. There is a pointer over the spindle, which moves over a graduated scale. The no. of turns in the fixed coil be subject to on the range of the apparatus. But for the transmission has higher current requirements over the coil, less no of turns are sufficient. The controlling torque is generated by the springs as well as gravity control used for vertically mounted panel type instruments. Damping torque is provided by air friction. The construction is shown below:

Working Principle–

When current is passing through the coil is proportional to the quantity to be measured then the coil becomes an electro magnet. The electro magnet attracts soft iron piece towards it; thus, producing deflecting torque.

The soft iron piece linked to the spindle, hence as iron portion becomes attracted, spindle travels and hence pointer to the spindle gets deflected. If the direction of current is opposite, the magnetic field by current carrying coil will be in opposite direction. But for any direction of magnetic field, iron pieces are going to attract towards magnet. Hence deflection torque is always unidirectional. Hence these instruments well suit ac and as well as dc measurements.

 Electrodynamic type Instrument:

• Fixed Coils type – the essential a uniform field for the operation of this instrument is generated by the fixed coil. Henceforth, a uniform field will create adjacent the Centre of that coil.
• Moving Coil type– This is wound either as a coil of self-sustainment or non-metallic former type.
• Controlling torque type – the controlling torque is providing by the springs.
•  Moving Coil – the moving coil will be mounted on the aluminum spindle. It comprises of counter weight mechanism and a specific pointer.
• Damping torque – the damping torque is providing by the friction of air. This will be produced by the help of aluminum vanes pair linked to the spindle at the end.
• Shielding Mechanism– Usually generated field in the instrument is very feeble. Earth’s magnetic field impacts the reading. So, shielding is employed to reduce stray-magnetic field in the selected location.
• The Cases and Scales – This usually polished wooden or metal cases, and rigid casing. 

To read more about electronics and electrical related articles click here

1.     Which instrument is used for both ac and dc measurements?

1. The Moving iron
2. The Electrodynamometer
3. An Electrostatic Instruments
4. All of these types

Correct Answer is Option (4) :All of these types

2.     Maxwell bridge can be used for measurement of inductance with

1. Higher Q-factor
2. Very small Q-factor
3. Intermediate Q-factor
4. Variations in Q

Correct Answer is Option (3):Intermediate Q-factor

3.     Which type of bridge is utilized to measure freq. of a signal?

1. A Wien bridge
2. An Anderson’s bridge
3. A DesSauty’s bridge
4. Not an option

Correct Answer is Option (1):Wien bridge

4.     The phenomena creeping is observed in

1. A Watt-hour meter
2. A Volt meter
3. An Ammeter
4. The Q meter

Correct Answer is Option (1):A Watt-hour meter

5.     Low resistance in any system is measured

1. by the Wheatstone bridge
2. by the Kelvin double bridge
3. by the Maxwell bridge
4. by the Wien bridge

Correct Answer is Option (2): by the Kelvin double bridge

6.     Thermocouple is a

1. Passive transducer
2. Active transducer
3. Piezoelectric transducer
4. None of these

Correct Answer is Option (2) : Active transducer

7.     Energy meter is an

1. Integrating instrument
2. Recording instrument
3. Indicating instrument
4. None of these

Correct Answer is Option (1) : Integrating instrument

8.     A megger, which is a measurement instrument, is used to measure

1. Low value resistance
2. Medium value resistance
3. High value resistance
4. All of these

Correct Answer is Option (3) :High value resistance

9.     _____ is not an integrating instrument?

1. Ampere-hour meter
2. Watt-hour meter
3. Voltmeter
4. All of these

Correct Answer is Option (2) : Watt-hour meter

10. ______ is not suitable for both ac and dc signal measurements?

1. Dynamometer
2. Electrostatic type
3. Induction type
4. None of these

Correct Answer is Option (3) : Induction type

11. Which bridge is used for freq. measurement?

1. Maxwell bridge
2. Schering bridge
3. Wien bridge
4. Anderson bridge

Correct Answer is Option (3) : Wien bridge

12. The scale of PMMC instrument is

1. Uniform
2. Cramped at the ends
3. linear
4. None of these

Correct Answer is Option (3) : linear

13.  A megger’s function is to

1. Measure voltage
2. Measure current
3. Measure insulation resistance
4. None of these

Correct Answer is Option (3):Measure insulation resistance

14. One useful advantage of PMMC instrument is

1. Low power consumption
2. No hysteresis loss
3. Efficient eddy current damping
4. All of these

Correct Answer is Option (4) : All of these

15.  A repulsion type ammeter when used in an ac circuit, reads

1. Peak value current
2. RMS value current
3. Mean value
4. None of these

Correct Answer is Option (2) : RMS value current

16.  Which following parameter can be measure by using the Maxwell bridge?

1. Value of the unknown Resistor
2. Value of unknown Inductor
3. Value of unknown Capacitor
4. Value of Freq.

Correct Answer is Option (2) : Value of unknown Inductor

17. In a moving iron instrument, 12A current causes a deflection of the needle by 60 degree. A deflection of 15 degree will be obtained by a current of

1. 9A
2. 6A
3. 4A
4. 3A

Correct Answer is Option (2) : 6A

18. An ac voltmeter is used to measure

1. Average value
2. RMS value
3. Peak value
4. Peak to peak value

Correct Answer is Option (2) : RMS value

19.  Which of the characteristics is desirable during any electrical measurement?

1. Accuracy
2. Sensitivity
3. Reproducibility
4. All of these

Correct Answer is Option (4) : All of these

20.  Which measuring instruments is utilized high AC voltage measurements?

1. PMMC voltmeter
2. Moving iron voltmeter
3. Electrostatic voltmeter
4. Hot wire instrument

Correct Answer is Option (3) : Electrostatic voltmeter

21.  In electrodynamometer type wattmeter

1. Current coil is fixed
2. Pressure coil is fixed
3. Both of these are fixed
4. Both of these are movable

Correct Answer is Option (4) : Both of these are movable

22.  Which of the following bridge is preferred for the measurement of inductance having Q factor?

1. Maxwell’s bridge
2. Hay bridge
3. Owen bridge
4. Desauty’s bridge

Correct Answer is Option (2) :Hay bridge

23. Electrostatic type instruments are

1. Ammeters
2. Wattmeter
3. Voltmeters
4. Ohmmeter

Correct Answer –Option (3) : Voltmeters

24.  A moving iron attraction type instrument is made of

1. One moving coil and one iron piece
2. Two moving coils
3. Two iron pieces
4. All of these

Correct Answer is Option (1) : One moving coil and one iron piece

25.  In a chopper type dc voltmeter, the voltage conversion is

1. Ac to DC
2. DC to AC
3. Only AC or DC
4. None of these

Correct Answer is Option (2) : DC to AC

For more Electronics Questions click here

Click here for Recent post

Points of Discussion: Microwave Resonators

• Introduction to Microwave Resonators
• Series Resonator Circuit
• Parallel Resonator Circuit
• Transmission Line Resonators
• Solved Mathematical Example of Microwave Resonators

Introduction to Microwave Resonators

Microwave resonators are one of the crucial elements in microwave communication circuit. They can create, filter out, and select frequencies in various applications, including oscillators, filters, frequency meters, and tuned oscillators.

Operations of microwave-resonators are very much like the resonators used in network-theory. We will discuss the series and parallel RLC resonant circuits at first. Then, we will find out various applications of resonators at microwave frequencies.

Know about Microwave Engineering and Its Overview. Click Here!

Series Resonator Circuit

A series resonator circuit is made by arranging a resistor, an inductor, and a capacitor in series connection with a voltage source. The circuit diagram of a series RLC is given below. It is one of the type of microwave resonators.

The input impedance of the circuit is given as Z_in = R + jωL − j /ωC

The complex power from the resonator is given by P_in.

P_in = ½ VI* = ½ Z_in | I|2 = ½ Z_in | (V/Z_in) |²

Or, P_in = ½ |I|² (R + jωL − j /ωC)

The power by the resistor is: P_loss = ½ |I|² R

The average magnetic energy stored by the inductor L is:

W_e = ¼ |V_c|² C = ¼ |I|² (1/ω²C)

Here, V_c is the voltage across the capacitor.

Now, complex power can be written as follow.

P_in = P_loss + 2 jω (W_m − W_e)

Also, the input impedance can be written as: Z_in = 2P_in/ |I|²

Or, Z_in = [P_loss + 2 jω (W_m − W_e)] / [½ |I|²]

In a circuit, resonance occurs when the stored average magnetic field and the electric charges are equal. That means, W_m = W_e. The input impedance at resonance is: Z_in = P_loss / [½ |I|²] = R.

R is a pure real value.

At W_m = W_e, the resonance frequency ω₀ can be written as ω ₀ = 1/ √(LC)

Another critical parameter of the resonant circuit is the Q factor or quality factor. It is defined as the ratio of the average energy stored to the energy loss per second. Mathematically,

Q = ω * Average energy change

Or Q = ω *(W_m + W_e) / P_loss

Q is a parameter which gives us the loss. Higher Q value implies the lower loss of the circuit. Losses in a resonator may occur due to loss in conductors, dielectric loss, or radiation loss. An externally connected network may also introduce losses to the circuit. Each of the losses contributes to the lowering of the Q factor.

The Resonator’s Q is known as Unloaded q. It is given by Q₀.

The unloaded Q or Q₀ can be calculated from the previous equations of Q factor and Power loss.

Q₀ = ω ₀ 2W_m / P_loss = w₀L / R = 1/ w₀Rc

From the above expression, we can say that the Q decreases with the increase of R.

We will now study the behaviour of the input impedance of the resonator circuit when it is near its resonance frequency. Let w = w0 + Δω, here Δω represents a minimal amount. Now, the input impedance can be written as:

Z_in = R + jωL (1 − 1/ω²LC)

Or Z_in = R + jωL ((ω² – ω₀²)/ω²)

Now, ω²₀ = 1/LC and ω² − ω²₀ = (ω − ω₀) (ω + ω₀) = Δω (2ω − Δω)2ω Δω

Z_in ~ R + j²L Δω

Z_in ~ R + j²RQ₀L Δω / ω₀

Now, the calculation for half-power fractional bandwidth of the resonator. Now, if the frequency becomes |Z_in| ² = 2R², the resonance receives 50% of the total delivered power.

One more condition is such that when the Band Width value is in fraction, the value of Δω/ω₀ becomes half of the Band Width.

|R + jRQ₀(BW)| ² = 2R²,

or BW = 1/Q₀

Know about Transmission Lines and waveguides. Click Here!

Parallel Resonant Circuit

A parallel resonator circuit is made by arranging a resistor, an inductor, and a capacitor in parallel with a voltage source. The circuit diagram of a parallel RLC is given below. It is one of the type of microwave resonators.

Z_in gives the input impedance of the circuit.

Z_in = [1/R + 1/jωL + jωC] ⁻¹

The complex power delivered from resonator is given as P_in.

P_loss = ½ VI* = ½ Z_in | I|² = ½ Z_in | V|² / Z_in*

Or P_in = ½ |V|² (1/R + j/wL – jωC)

The power from resistor R is P_loss.

P_loss = ½ |V|² / R

Now, the Capacitor also stores the energy, it is given by –

W_e = ¼ |V|²C

The inductor also stores the magnetic energy, it is given by –

W_m = ¼ |I_L|² L = ¼ |V|² (1/ ω²L)

IL is the current through the inductor. Now, the complex power can be written as: P_in = P_loss + + 2 jω (W_m − W_e)

The input impedance can also be written as: Z_in = 2P_in/ |I|² = (P_loss + 2 jω (W_m − W_e))/ ½ |I|²

In the series circuit, the resonance occurs at W_m = W_e. Then the input impedance at resonance is Z_in = P_loss / ½ |I|² = R

And the resonant frequency at W_m = W_e can be written as w₀ = 1 / √ (LC)

It is same as the value of series resistance. Resonance for the parallel RLC circuit is known as an antiresonance.

The concept of unloaded Q, as discussed early, is also applicable here. The unloaded Q for the parallel RLC circuit is represented as Q₀ = ω₀²W_m/ P_loss.

Or Q₀ = R /ω₀L = ω₀RC

Now, at antiresonance, “W_e = W_m”, and the value of the Q factor decreases with the decrease in R’s value.

Again, for input impedance near resonance frequency consider ω = ω₀ +Δω. Here, Δω is assumed as a small value. The input impedance is again rewritten as Z_in.

Z_in = [ 1/R + (1 – Δω / ω₀) / jω₀L + jω₀C + jΔωC] ^-1

Or Z_in = [ 1/R + j Δω / ω2L + jΔωC] ^{– 1}

Or Z_in = [ 1/R + 2jΔωC]^-1

Or Z_in = R / (1 + 2jQ₀Δω/ω₀)

Since ω² = 1/LC and R = infinite.

Z_in = 1 / (j²C (ω – ω₀))

The half-power bandwidth edges occur at frequencies (Δω / ω₀ = BW/2) such that, |Z_in|² = R²/ 2

Band Width = 1 / Q₀.

Transmission Line Resonators

Almost always, the perfect lumped components can not deal in the range of microwave frequencies. That is why distributed elements are used at microwave frequency ranges. Let us discuss various parts of transmission lines. We will also take into consideration of the loss of transmission lines as we have to calculate the resonators’ Q value.

For Detail Analysis of Transmission Lines… Click Here!

Short circuited λ/2 Line

Let us take a transmission line which suffers loss and also it is short-circuited at one of its terminal.

Let us assume the transmission line has a characteristic impedance of Z₀, the propagation constant of β and attenuation constant is α.

We know that, at resonance, the resonant frequency is ω = ω₀. The length of the line ‘l’ is λ/2.

The input impedance can be written as Z_in = Z₀ tanh (α + jβ)l

Simplifying the tangential hyperbolic function, we get Z_in.

Z_in = Z₀ (tanh αl + j tan βl) / (1 + j tan βl tanh αl).

For a lossless line, we know that Z_in = jZ₀ tan βl if α = 0.

As discussed earlier, we will consider the loss. That I why, we will take,

αl << 1 and tanh αl = αl.

For a TEM line,

βl = ωl/ v_p = ω₀l/ v_p + Δωl/ v_p

v_p is an important parameter which represents the transmission line’s phase velocity. L = λ/2 = πv_p/ω₀ for ω = ω₀, we can write,

βl = π + Δωπ/ ω₀

Then, tan βl = tan (π + ωπ/ ω₀) = tan (ωπ/ ω₀) = ωπ/ ω₀

Finally, Z_in = R + 2 jLω

At last, the value of resistance comes as: R = Z₀αl

The value of inductance comes as : L = Z₀π/ 2ω₀

And, the value of Capacitance comes as : C = 1/ ω²₀L

The unloaded Q of this resonator is, Q₀ = ω₀L/ R = π/ 2αl = β/ 2α

Solved mathematical Example of Microwave Resonators

1. A λ/2 resonator is made up of copper coaxial line. Its inner radius is 1 mm, and the outer radius is 4mm. The value of the resonant frequency is given as 5 GHz. Comment on the calculated Q value of two coaxial line among which one is filled with air another filled with Teflon.

Solution:

a = 0.001, b = 0.004, η = 377 ohm

We know that the conductivity of the copper is 5.81 x 107 S/m.

Thus, the surface resistivity at 5GHz = Rs.

Rs = root (ωµ0/ 2σ)

Or Rs = 1.84 x 10-2 ohm

Air filled attenuation,

αc = Rs /2η ln b/a {1/ a + 1/ b}

Or αc = 0.22 Np/m.

For Teflon,

Epr = 2.08 and tan δ = 0.0004

αc = 0.032 Np/m.

There is no dielectric los due to air filled, But for Teflon-filled,

αd = k0 √epr/2 * tan δ

αd = 0.030 Np/m

So, Q_air = 104.7 / 2 * 0.022 = 2380

Q_tefflon = 104.7 * root(2.008) / 2 * 0.062 = 1218

Points of Discussion : Transmission lines and Waveguides

• Introduction to Transmission lines and Waveguides
• Types of Waveguides
• Types of transmission lines
• Parallel Plate Waveguide
• Rectangular Waveguide
• Circular Waveguide

Detail analysis of Transmission Lines! Check out here!

Introductions to Transmission Lines(TL) & Waveguide(WG)

The invention and development of transmission lines and other waveguides for the low-loss transmission of power at high frequency are among the earliest milestones in the history of microwave engineering. Previously Radio Frequency and related studies were revolved around the different types of transmission medium. It has advantages for controlling high power. But on the other hand, it is inefficient in controlling at lower values of frequencies.

Two wires lines cost less, but they have no shielding. There are coaxial cables that are shielded, but it is difficult to fabricate the complicated microwave components. Advantage of Planar line is that it has various versions. Slot lines, co planar lines, micro-strip lines are some of its forms.  These types of transmission lines are compact, economical, and easily integrable with active circuit devices.

Parameters like constant of propagation, characteristic impedance, attenuation constants consider how a transmission line will behave. In this article, we will learn about the various types of them. Almost all transmission lines (who have multiple conductors) are capable of supporting the transverse electromagnetic waves. The longitudinal field components are unavailable for them. This particular property characterizes the TEM lines and wave-guides. They have a unique voltage, current, and characteristic impedance value. Waveguides, having a single conductor, may support TE (transverse electric) or TM (transverse magnetic), or both. Unlike Now, Transverse Electric and Transverse Magnetic modes have their respective longitudinal field components. They are represented by that property.  

Know about 7+ Applications of Microwave Engineering and Overview. Click Here!

Types of waveguides

Though there are several types of waveguides, some of the most popular are listed below.

• Parallel Plate Waveguide
• Rectangular waveguide
• Circular Waveguide

Types of Transmission Lines

Some of the types of transmission lines are listed below.

• Stripline
• Microstrip line
• Coaxial line

Parallel Plate Waveguide

Parallel plate waveguide is one of the popular types of waveguide, which are capable of controlling both Transverse Electric and Transverse magnetic modes. One of the reason behind the popularity of parallel plate waveguide is that they have applications in model making for the greater-order modes in lines.

The above image (Transmission lines and waveguides) shows the geometry of the parallel plate waveguide. Here, the strip width is W and considered more significant than the separation of d. That is how fringing field and any x variables can be cancelled. The gap between two plates is filled up by a material of permittivity ε and permeability of μ.

TEM Modes

The solution of the TEM Modes is calculated with the help of solution of the Laplace’s equation. The equation is calculated considering the factor for the electrostatic voltage which lies in between the conductor plates.

Solving, the equation, the transverse electric field comes as:

e^– (x,y) = ∇_t ϕ (x,y) = – y^{^} V_o / d.

Then, the total electric field is: E^– (x, y, z) = h^– (x, y) e^{– jkz} = y^{^} (V_o / d) * e^-jkz

k represents the propagation constant. It is given as: k = w √ (μ * ε)

The magnetic fields’ equation comes as:

Here, η refers to the intrinsic impedance of the medium which lies in between the conductor plates of parallel plate waveguides. It is given as: η = √ (μ / ε)

TM Modes

Transverse magnetic or TM modes can be characterized by H_z = 0 and a finite electric field value.

(∂² / ∂y² + k²_c) e_z (x, y) = 0

Here kc is the cut-off wavenumber and given by k_c = √ (k² − β²)

After the solution of the equation, the Electric filed E_X comes as:

E_z (x, y, z) = A_n sin (n * π * y / d) * e^{– jβz}

The transverse field components can be written as:

H_x = (jw ε / k_c) A_n cos (nπy / d)  e^{– jβz}

E_y = (-jB/ k_c) A_n cos (nπy / d) e^{– jβz}

E_x = H_y = 0.

The cut off frequency of TM mode can be written as:

f_c= k_c / (2π * √ (με)) = n / (2d * √(με))

The wave impedance comes as Z_TM = β / ωε

The phase velocity: v_p = ω / β

The guide wavelength: λ_g = 2π / β

TE Modes

H_z (x,y) = B_n cos (nπy / d) e^{– jβz}

Equations of the transverse fields are listed below.

The propagation constant β = √ (k2 – (nπ/d )²)

The cutoff frequency: f_c = n / (2d √ (με))

The impedance of the TM mode: Z_TE = E_x / H_y = k_n/ β = ωμ/ β

Rectangular waveguide

The rectangular waveguide is one of the primary types of waveguide used to transmit microwave signals, and still, they have been used.

With miniaturization development, the waveguide has been replaced by planar transmission lines such as strip lines and microstrip lines. Applications which uses highly rated power, which uses millimeter wave technologies, some specific satellite technologies still use the waveguides.

As the rectangular waveguide has not more than two conductors, it is only capable of Transverse Magnetic and Transverse Electric Modes.

TE Modes

The solution for H_z comes as: H_z (x, y, z) = A_mn cos (mπx/a) cos (nπy/b) e^{– jβz}

Amn is a constant.

The field components of the TEmn modes are listed below:

The propagation constant is,

TM Modes

The solution for E_z comes as: E_z (x, y, z) = B_mn sin (mπx/a) sin (nπy/b) e^{– jβz}

Bmn is constant.

The field component of TM mode are calculated as below.

Propagation constant :

The wave impedance: Z_TM = E_x / H_y = -E_y / H_x = bη * η / k

Circular Waveguide

The circular waveguide is a muffled, round pipe structure. It supports both the TE and TM modes. The below image represents the geometrical description of a circular waveguide. It has an inner radius ‘a,’ and it is employed in cylindrical coordinates.

E_ρ = (− j/ k²_c) [ β ∂E_z/ ∂ρ + (ωµ/ρ) ∂ H_z/ ∂φ]

E_ϕ = (− j/ k²_c) [ β ∂E_z/ ∂ρ – (ωµ/ρ) ∂ H_z/ ∂φ]

H_ρ = (j /k²_c) [(ωe/ ρ) ∂E_z /∂φ − β ∂ H_z/ ∂ρ]

H_ϕ = (-j /k2_c) [(ωe/ ρ) ∂E_z /∂φ + β ∂ H_z/ ∂ρ]

TE Modes

The wave equation is:

∇²H_z + k²H_z = 0.

k: ω√µe

The propagation constant: B_mn = √ (k² – k_c²)

Cutoff frequency: fc_nm = k_c / (2π * √ (με))

The transverse field components are:

E_p = (− jωµn /k²_cρ) * (A cos nφ − B sin nφ) J_n (k_cρ) e^{− jβz}

H_φ = (− jβn/k²_cρ) (A cos nφ − B sin nφ) J_n (k_cρ) e^{− jβz}

The wave impedance is:

Z_TE = E_p / H_ϕ = – E_ϕ / H_p = ηk / β

TM Modes

To determine the necessary equations for the circular waveguide operating in Transverse magnetic modes, the wave equation is solved and the value of Ez is calculated. The equation is solved in cylindrical coordinates.

[∂² /∂ρ² + (1/ρ) ∂/ ∂ρ + (1 /ρ²) ∂²/ ∂φ² + k²c] e_z = 0,

TM_nm Mode’s Propagation Constant ->

βnm = √ (k² – kc²) = √ (k² − (p_nm/a)²)

Cutoff frequency: f_cnm = k_c / (2π√µε) = p_nm / (2πa √µε)

The transverse fields are:

E_ρ = (− jβ/ k_c) (A sin nφ + B cos nφ) J_n^/ (k_cρ) e^{− jβz}

E_φ = (− jβn /k²_cρ) (A cos nφ − B sin nφ) J_n (k_cρ) e^{− jβz}

H_ρ = (jωen /k² _cρ) (A cos nφ − B sin nφ) J_n (k_cρ) e^{− jβz}

H_φ = (− jωe/ k_c) (A sin nφ + B cos nφ) Jn` (k_cρ) e^{− jβz}

The wave impedance is Z_TM = E_p / H_φ = – E_ϕ/H_p = ηβ/k

Stripline

One of the examples of planar type transmission line is Stripline. It is advantageous for incorporation inside microwave circuits. Stripline can be of two types – Asymmetric Stripline and Inhomogeneous stripline. As stripline has two conductors, thus it supports the TEM mode. The geometrical representation is depicted in the below figure.

Points of Discussion

• Introduction to Microwave Engineering
• A brief history of Microwave Engineering
• Properties of Microwave Engineering
• Advantages and Disadvantages of Microwave Engineering
• Applications of Microwave Engineering
• Frequently asked questions on Microwave Engineering.

Introduction to Microwave Engineering

The microwave frequency range is typically 100 Mega Hertz to 1000 Giga Hertz. The range covers not only the microwave domain but also the radio frequency domain. Typical microwave domain has a frequency range of 3 MHz to 300 GHz. The corresponded electrical wavelength lies between 10 cm to 1mm. Signals having millimetre wavelengths are frequently referred to as millimetre waves. Because of the high-frequency range, typical circuit theory problems cannot solve the microwave engineering problems.

Microwave components generally act as distributed elements. The phenomena occur when the current and voltage phase varies. At lower frequencies, the wavelength gets larger. That is why there are insignificant phase changes across the dimension of the device.

Maxwell’s Theorems are one of the most used theorems in this domain.

A brief history of Microwave Engineering

Microwave engineering is one of the young and prosperous fields of engineering. The development started almost 50 years ago.The progress in this digital era in various fields is helping the microwave and RF domain to be live.

In the year 1873, James Clerk Maxwell came up with the fundamentals of Electromagnetic Theory. In the United States, a unique laboratory named as – Radiation Laboratory, was set up at the Massachusetts Institute of Technology to study, research and develop the Radar Theory. Various renowned scientists including – H. A. Bethe, R. H. Dicke, I. I. Rabi, J. S. Schwinger and several prominent scientists were there for the development in the field of RF and Microwave at that time.

Communication technologies using microwave systems started developing soon after the invention of Radar. The wide bandwidths, line-of-sight propagation of microwave technologies have proved to be necessary for both terrestrial and satellite communications. Nowadays the researches are going on the development of economic miniaturized microwave components.

Properties of Microwaves

Microwave Engineering deals with microwave signals. Let’s analyse some of the characteristics of microwave domain. 

1. Microwave signals have shorter wavelengths.
2. The ionosphere cannot reflect the microwave.
3. Microwave signals get reflected by the conducting surfaces.
4. Microwave signals get attenuated easily within shorter distances.
5. A thin layer of cable is enough for transmission of microwave signals.

Know about transmission lines. Click Here!

Advantages and Disadvantages of Microwave Engineering

Microwave engineering comes up with both its advantages and disadvantages. They are discussed in the later sections.

Advantages of Microwave Engineering

Microwaves have several advantages over any other domains. Let us discuss some of them.

1. Microwave has a broader bandwidth. Thus, more data can be transmitted. For this advantage, microwave signals are used in point-to-point communications.
2. Microwave antennas have higher gain.
3. Size of the antenna gets reduced as the frequencies are higher and the wavelength is shorter.
4. As microwave lie in HF to VHF, very small amount of power is consumed.
5. Microwave signals allow having an effective reflection area for the radar systems.
6. Line of sight propagation helps to reduce the effect of fading.

Disadvantages of Microwaves

Microwave engineering has some limitations also. Let us discuss some of them.

1. Microwave resources are significantly costlier. Also, installation charges are high for several types of equipment.
2. Microwave devices and systems are significant and occupy more space. However, researches are on for less space consumed devices.
3. Microwave systems some time suffers electromagnetic interference.
4. Inefficiency due to electric power may cause.

Applications of Microwave Engineering

High frequencies and shorter wavelengths of microwave systems create difficulties in circuit analysis. But these unique characteristics provide opportunities for the application of the microwave system. The below-mentioned considerations could be useful for practices.

• The antenna has a property that the antenna’s gain is proportionally related to the size of the antenna. Now, for higher operational frequency, antenna gain is comparatively larger for a given physical antenna size. It also has significant consequences when implementing a microwave system.
• More bandwidth (which is again directly related to the data rate) is gained at higher frequencies. 1% BW of 500 Mega Hertz means 5 Mega Hertz. It can give data rate around 5 Megabyte Per Second.
• Microwave has the property of line of sight, and the ionosphere cannot reflect them.
• One of the property of microwave signals, coupled with a gain of antennas, makes it unique and preferable.
• Different types of resonances like molecular, atomic and nuclear happen at microwave frequency ranges. This opens up the field for several applications in basic science, remote sensing, medical science etc.

1. The primary application of RF and Microwaves in today’s world is in wireless technologies. Technologies like – wireless communications, wireless networking, wireless security systems, radar systems, medical engineering, and remote sensing.
   • Modern day’s telephony system is evolved with the concept of cellular frequency reuse, proposed in 1947 at Bell labs. But it was practically implemented in the year 1970. In the mean-time, the demand for wireless communication increased, and miniaturization of devices was developed. Later, various communications like – 2G, 2.5G, 3G, 3.5G, 3.75G, 4G were developed using the microwave system.
2. Satellite communications are also dependent on RF and microwave technologies. Satellites have been developed for providing cellular data, videos, data connections for the whole world. Small satellite systems like GPS and DBS has been doing great.
3. Wireless local networks or WLANs connects computers within a short distance and provides high-speed networking. It is also an application of microwaves. Demand for WLANs are increasing day by day and will have high demands in future too.
4. Another application of microwaves is ultra-wideband radio. Here the broadcast signal takes a vast frequency band but has a low power level. It is a precaution for avoiding interference with other systems.
5. Radar & Military Applications: Radar systems have several applications in Defence and Militant fields, also in  profitable and research based fields. Radar is typically used to detect and mark any foreign objects inside the user’s territory in air and ground. It is also used in missile guidance and fire controls.
6. In the commercial fields, radar systems are used in ATC (air traffic control), motion detection (like- opening and closing of the door, security alarms), vehicle collision avoidance, measurement of the distance from a point.
7. Microwave radiometry is another application.

Frequently asked questions on Microwave Engineering

1. What is the frequency range for RF and microwaves?

• Answer: RF ranges from 30 MHz to 300 MHz, and Microwaves ranges from 300 MHz to 300 GHz.

2. What are the frequency bands of microwaves?

• Answer: There are 13 different frequency bands in the microwave range. The below list illustrates them.

Band Name	Range of frequency	Range of Wavelength
L Band	1 Giga Hertz – 2 Giga Hertz	15 cm to 30 cm
D Band	110 Giga Hertz– 170 Giga Hertz	1.8 mm to 2.7 mm
Ku Band	12 Giga Hertz – 18 Giga Hertz	16.7 mm to 25 mm
K Band	18 Giga Hertz – 26.5 Giga Hertz	11.3 mm to 16.7 mm
S-Band	2 Giga Hertz – 4 Giga Hertz	7.5 cm to 15 cm
Ka-Band	26.5 Giga Hertz – 40 Giga Hertz	5 mm to 11.3 mm
Q Band	33 Giga Hertz – 50 Giga Hertz	6 mm to 9 mm
C Band	4 Giga Hertz – 8 Giga Hertz	3.75 cm to 7.5 cm
U Band	40 Giga Hertz – 60 Giga Hertz	5 mm to 7.5 mm
V Band	50 Giga Hertz – 75 Giga Hertz	4 mm to 6 mm
W Band	75 Giga Hertz – 110 Giga Hertz	2.7mm to 4.0 mm
X Band	8 Giga Hertz – 12 Giga Hertz	25 cm to 37.5 cm
F Band	90 Giga Hertz – 110 Giga Hertz	2.1 mm to 3.3 mm

3. Mention some disadvantages of microwaves.

• Answer: Microwave engineering has some limitations also. Let us discuss some of them.

1. Microwave resources are significantly costlier. Also, installation charges are high for several types of equipment.
2. Microwave devices and systems are significant and occupy more space. However, researches are on for less space consumed devices.
3. Microwave systems some time suffers electromagnetic interference.
4. Inefficiency due to electric power may cause.

Cover Image By: WINDOWSCUSTOMIZATION

Topic of Discussion: Digital Modulation Techniques

What is Digital Modulation?

Define Digital Modulation:

 “The conversion of analog signal to digital signal is basically known as digital modulation in which a digital signal consists of binary digits.”

Fundamental Digital Modulation Methods:

What are the different techniques of modulating in digital communication?

 The most important methods of digital modulations are:

• PSK (Phase Shift Keying) – In this Digital Modulation a certain number of phases are used.
• FSK (Frequency Shift Keying) – In this shift keying method, an exact or limited number of frequencies are used.
• ASK (Amplitude Shift Keying) – In this shift keying method, an exact & limited number of amplitudes are used.
• QAM (Quadrature Amplitude Modulation) – Here minimum 2 separate phase and 2 separate amplitude are taken.

What is QPSK Modulation?

Explain the working of QPSK:

 QPSK is a digital modulation technique in which two successive bits in the data sequence are grouped together so as to achieve better bandwidth efficiency. As the bits are grouped together to form symbols, the bit rate or signaling rate (f_b) is reduced which reduces the bandwidth of the channel.

 QPSK may be treated as an M-array PSK modulation scheme in which M=4. In a QPSK system, if we combine two successive bits, as a result we will get four distinct symbols. As one symbol changes to the next symbol, the phase of the carrier changes by 90˚ or π/2 radian. Each symbol is called a di-bit.

As an example, the four di-bits may be 00, 01, 11 in natural coded form or 00, 10, 11, 01 in Gray encoded form may be represented as shown below:

QPSK signals can be expressed as

S(t) = A_c cos Ø(t) 2πf_ct – A_c sin Ø (t) sin ) 2πf_ct

Where, A_c cos Ø (t) forms the in-phase component and A_c sin Ø (t) forms the quadrature component. The QPSK signals can be generated based on the in-phase and quadrature components as well.

What is coherent detection technique?

Describe ASK demodulation through coherent detection:

 In coherent detection technique, a local carrier is used for detection. A local carrier signal made at the receiver’s end and will be phase-locked at the transmitter’s end. The received signal is heterodyned with the local carrier to generate the baseband signal.

The coherent detection of ASK is a locally generated signal of the same frequency and phase as the transmitted signal is applied to a product modulator as shown below

The integrator integrates the output signal of the product modulator over a bit interval, T_b and the output of the integrator is compared with the pre-set threshold in a decision device. If the threshold gets exceeded, it gives 1 as a symbol & if the threshold is not exceeded it gives 0.

A synchronous or coherent detector should have two forms of synchronization; phase synchronization. Phase synchronization is necessary because it ensures locking in phase of the locally generated carrier wave with the transmitted signal. Timing synchronization is one of the most important factor here because it gives a fixed and particular timing of the decision-making operation in the receiver with respect to the switching instants.

Why is DPSK scheme of carrier modulation has been used?

DPSK in Modulation Technique:

We know there is a requirement of synchronization of phase in coherent receiver with BPSK without any discrete carrier term. A phase lock loop circuit may be used to extract the carrier reference only if a low-level pilot carrier is transmitted along with the BPSK signal.

In absence of a carrier, a squaring loop may be used to synchronize the carrier reference from this BPSK signal for providing coherent detection. But this introduces a 180˚ phase ambiguity. In order to eliminate this problem of 180˚ phase ambiguity a differential coding technique is used at the transmitter and a differential decoding is used at the receiver. This signaling technique of combining differential encoding with phase shift keying (PSK) is called differential phase shift keying or DPSK.

In DPSK, the input sequence of the binary bits is arranged in a way that the next bit has to rely on the previous bit. In the receiver’s end, the opposite happens i.e., the earlier received bit is utilized for detection of the current bits.

What are the advantages of PSK over ASK?

• ü  Phase Shift Keying is used to carry data over RF signal more efficiently than other modulation types. Hence this method is power effective.
• In PSK, less errors occur compared to ASK modulation and also occupies the same bandwidth as ASK.
• Better rate of data transmission usually attained by PSK i.e., QPSK, 16 QAM etc.

What are the major differences between QAM and QPSK?

 QAM differs with QPSK in the matter of spectral-width.

• The QPSK’s spectral width is wider than the QAM.
• Additionally, QAM has high Bit Error Rate than QPSK.

What are the major differences between QPSK and PSK?

• For Phase Shift Key, the shift of phases occur in 180 degrees. In case of QPSK, the shift is multiple of Ninety Degrees.
• QAM is a group of Amplitude Shift Key and Phase Shift Key.

Comparison of Binary Modulation and M-Array Modulation:

• The word binary signifies two-bits. Binary Modulation is the type of digital modulation technique.
• M simply denotes a digit that matches to the number of combinations possible for a specified number of binary variables. M-Array Modulation is the type of digital modulation technique

 What are the differences between MSK and QPSK?

Performance metrics for digital modulation scheme:

 The bit error rate, power spectra and bandwidth efficiency are some of the performance metrics of digital communication system. The desirable characteristic’s

1. BER should be good and in limit.
2. Signal transmission should happen including lesser transmission bandwidths.
3. There should be use of Minimal amount of transmission power.
4. The system should be of less cost.

To know more about line coding click here

[Specially picked questions for GATE, JEE, NEET]

In the Circuit theory series, we have come across some fundamental yet essential rules, formulas, and methods. Let us find out some applications of them and understand them more clearly. The problems will be mainly on – KCL, KVL, Thevenin’s theorem, Norton’s theorem, Superposition theorem, Maximum Power Transfer Theorem.

Helping Hands for problem Solving on Circuit Theory:

1. Kirchhoff’s Laws: KCL, KVL
2. Pure AC Circuits
3. Thevenin’s Theorem
4. Norton’s Theorem
5. Superposition Theorem
6. Maximum Power Transfer Theorem
7. Millman’s Theorem
8. Star & Delta Connection

Circuit Theory: 1. Find out the maximum power which can be transferred to the load R_L for the below-given circuit. Apply required theorems of Circuit Theory.

• Solution: Remove the load resistor from the circuitry and voltage source to find out Equivalent Resistance.

So, the resistance or the impedance (AC Circuit) of the circuit through the open terminal:

Z_TH = 2 || j2 = (2 x j2) / (2 +j2) = j2 / (1 +j)

Or, Z_TH = 2 ∠90^o / √2 ∠45^o

Or, Z_TH = √2 ∠45^o

Now, we will calculate the current through the j2 ohms resistor.

I = 4 ∠0^o / (2 +j2)

Or, I = 2 / (1+j) = √2 ∠ – 45^o

The Thevenin’s equivalent voltage comes as V_TH = I * j2.

Or, V_TH = 2√2 ∠45^o V

Now we can redraw the circuit in Thevenin’s equivalent circuit.

Now, from power transfer theorem, R_L = | Z_TH| = √2 ohm for full power.

Now, The current through the load I_L = V_TH / (R_TH + R_L)

Or, I_L = 2√2 ∠45^o / (√2 + √2 ∠45^o)

OR, I_L = 2 ∠45^o / (1 + 1∠45^o)

OR, I_L = 2 ∠45^o / [ 1 + (1 + √2) + (j / √2)]

OR, I_L = 1.08 ∠22.4^o A

|I_L| = 1.08 So, the maximum power is: |I_L²| R_L = (1.08 x 1.08) x √2 = 1.65 W.

Kirchhoff’s Laws: KCL, KVL

Circuit Theory: 2. Find out Norton’s equivalent resistance at terminal AB, for the below-given circuit.

• Solution: At first, we will apply a voltage source at the open circuit at the AB terminal. We name it V_DC and assume I_DC flows from it.

Now, we apply Kirchhoff’s Current Law to do nodal analysis at node a. We can write,

(V_dc – 4I) / 2 + (V_dc / 2) + (V_dc / 4) = I_dc

Here, I = V_dc / 4

Or, 4I = V_dc

Again, (V_dc – V_dc) / 2 + V_dc / 2 + V_dc / 4 = I_dc

Or, 3V_dc / 4 = I_dc

And, V_dc / I_dc = R_N

Or, R_N = 4/3 = 1.33 ohm.

So, the Norton’s Equivalent Resistance is 1.33 ohms.

Circuit Theory: 3. Find out the value of R1 in Delta equivalent circuit of the given star connected network.

• Solution: This problem can be solved easily, using the star’s conversion formula to delta connection.

Let us assume, that R_a = 5 ohms, R_b = 7.5 ohms, and R_c = 3 ohms.

Now, applying the formula,

R₁ = R_a + R_c + (R_a * R_c / R_b)

Or, R₁ = 5 + 3 + (5 x 3) / 7.5

Or, R₁ = 5 + 3 + 2 = 10 ohms.

So, the R1 Delta Equivalent resistance is: 10 ohms.

Circuit Theory: 4. Find out the current flowing through the R2 resistor for the circuit given below.

• Solution: We have to use the idea of source transformation and Kirchhoff’s Voltage Law to find out the answer.

Let us assume ‘I’ Ampere current flows through the R2 (1 kilo-ohm resistor). We can say current through 2-kilo ohm resistance will be (10 – I) Ampere (As current from 10 A source will be 10 A). Similarly, current from 2 A quotation will be 2 A and thus current through 4-kilo ohm resistance will be (I – 2) Ampere.

Now, we apply Kirchhoff’s voltage law in the loop. We can write

I x 1 + (I – 2) x 4 + 3 x I – 2 x (10 – I) = 0

Or, 10I – 8 – 20 = 0

Or, I = 28/10

Or, I = 2.8 mA

So, the current through the R2 resistor is 2.8 mA.

Circuit Theory: 5. If the equivalent resistance for the infinite parallel ladder given in the below image is R_eq, calculate R_eq / R. Also find the value of R_eq when R = 1 ohm.

• Solution: To solve the problem, we must know the equivalent resistance of the infinite parallel ladder. It is given by R_E = R x (1 + √5)/2.

So, we can replace the circuit in the following one.

The equivalent resistance comes here: R_eq = R + R_E = R + 1.618R

Or, R_eq / R = 2.618

And when R = 1 ohm, R_eq = 2.618 x 1 = 2.618 ohm.

Circuit Theory: 6. A source voltage supplies voltage, V_s(t) = V Cos100πt. The source has an internal resistance of (4+j3) ohm. Find out the resistance of a purely resistive load, for transferring maximum power.

• Solution: We know that the power transmitted for a purely resistive circuit is the average power transferred.

So, R_L = √ (R_s² + X_s²)

Or, R_L = √ (4² + 3²)

Or, R_L = 5 ohm.

So, the load will be of 5 ohms.

Circuit Theory: 7.  Find out the Thevenin’s equivalent impedance between node 1 and 2 for the given circuit.

• Solution: To find the Thevenin’s equivalent impedance, we need to connect a voltage source of 1 volt in the place of node 1 and 2. Then we will calculate the current value.

So, Z_TH = 1 / I_TH

Z_TH is the desired resistance we have to find. I_TH is the current flowing due to the voltage source.

Now applying Kirchhoff’s Current law at node B,

i_AB + 99i_b – I_TH =0

Or, i_AB + 99i_b = I_TH ——- (i)

Applying KCL at node A,

i_b – i_A – i_AB = 0

or, i_b = i_A + i_AB ——- (ii)

From equation (i) and (ii) we can write,

i_b – i_A + 99i_b = I_TH

Or, 100i_b – i_A = I_TH ——- (iii)

Now, we apply Kirchhoff’s Voltage law at the outer loop,

10 x 103i_b = 1

Or, i_b = 10^-4 A.

And also,

10 x 103i_b = – 100i_A

Or, i_A = – 100i_A

From equation (iii), we can write,

100i_A + 100i_b = I_TH

Or, I_TH = 200i_b

Or, I_TH = 200 x 10^-4 = 0.02

So, Z_TH = 1 / I_TH = 1 / 0.02 = 50 ohms.

S, the impedance in-between node 1 and 2 is 50 ohms.

Circuit Theory: 8. A complex circuit is given below. Let us assume that both the voltage source of the circuit is in phase with each other. Now, the circuit is divided virtually in two-part A and B by the dotted lines. Calculate R’s value in this circuit for which maximum power is transferred from Part A to Part B.

• Solution: The problem can be solved in a few steps.

First, we find the current ‘i’ through R.

Or, i = (7 / (2 – R) A

Next, current through the 3V source,

i₁ = i – (3 / -j)

Or, i₁ = i – 3j

Then, we calculate the power transferred from Circuit B to A.

P = i²R + i₁ x 3

Or, P = [7 / (2 – R)]² x R + [7 / (2 – R)] x 3 —- (i)

Now, condition for transferring the maximum power is, dP / dR = 0.

So, differentiating equation (i) with respect to R, we can write:

[7 / (2 – R)]² + 98R/ (2 + R)² – 21/ (2 + R)² = 0

Or, 49 x (2 + R) – 98R – 21 x (2 + R)² = 0

Or, 98 + 42 = 49R + 21R

Or, R = 56 / 70 = 0.8 ohm

So, the R value for maximum power transfer from A to B is 0.8 ohm.

Check: Maximum Power Transfer Theorem

Circuit Theory: 9. Find out the value of the resistance for maximum power transferring. Also, find out the maximum delivered power.

• Solution: At the first step, remove the load and calculate the Thevenin’s Resistance. 

V_TH = V * R₂ / (R₁ + R₂)

Or, V_TH = 100 * 20 / (20 +30)

Or, V_TH = 4 V

The resistors are parallelly connected.

So, R_TH = R₁ || R₂

Or, R_TH = 20 || 30

Or, R_TH = 20 * 30 / (20 + 30)

Or, R_TH = 12 Ohms

Now the circuit is redrawn using the equivalent values. For maximum power transfer, R_L = R_TH = 12 ohms.

Maximum power P_MAX = V_TH² / 4 R_TH.

Or, P_MAX = 1002 / (4 × 12)

Or, P_MAX = 10000 / 48

Or, P_MAX = 208.33 Watts

So, the maximum delivered power was 208.33 watts.

Circuit Theory: 10. Calculate the load for maximum power transferring. Find out the transferred power also.

• Solution:

At the first step, remove the load, and calculate the Thevenin’s voltage now.

So, V_AB = V_A – V_B

V_A comes as: V_A = V * R₂ / (R₁ + R₂)

Or, V_A = 60 * 40 / (30 + 40)

Or, V_A = 34.28 v

V_B comes as:

V_B = V * R₄ / (R₃ + R₄)

Or, V_B = 60 * 10 / (10 + 20)

Or, V_B = 20 v

So, V_AB = V_A – V_B

Or, V_AB = 34.28 – 20 = 14.28 v

In the next step, calculation of resistance. As the rule says, remove the voltage and short circuit the connection.

R_TH = R_AB = [{R₁R₂ / (R₁ + R₂)} + {R₃R₄ / (R₃ + R₄)}]

OR, R_TH = [{30 × 40 / (30 + 40)} + {20 × 10 / (20 + 10)}]

OR, R_TH = 23.809 ohms

Now, draw the connection again with the calculated values. For maximum power transfer, R_L = R_TH = 23.809 ohms.

The load value will be = 23.809 ohms.

Maximum power is P_MAX = V_TH² / 4 R_TH.

Or, P_MAX = 14.282 / (4 × 23.809)

Or, P_MAX = 203.9184 / 95.236

Or, P_MAX = 2.14 Watts

So, the maximum delivered power was 2.14 watts.

Image Credit – Pravin Mishra, Milky Way Galaxy As Seen From Amphulaptsa Base Camp, CC BY-SA 4.0

Points of Discussion

• Introduction to Star & Delta Connection
• Star Connection
  • The relation between Phase Voltage and Link voltage of Star Connection
  • The relation between Phase Current and Link Current of Star Connection
• Delta Connection
  • The relation between phase voltage and line voltage of Delta connection
  • The relation between phase current and line current of Delta connection
• Difference Between Star and Delta Connections
• Conversion from star to delta and delta to star

Star delta connection | Star delta transformation

Introduction to Star Connection and Delta Connection

Star and delta connections are the two very well-known methods for establishing a three-phase system. They are an essential and widely used system. This article will discuss the basics of both star and delta connections and relations between phase and link voltage and current within the system. We will also find out the significant differences between star and delta connection.

Star Connection

Star connection is the method where the similar types of terminals (all three windings) are connected to a single point, known as star point or neutral point. There are also line conductors, which are the free three terminals. The designing of wires at the external circuits makes it a three phase, three wire circuit and makes the star connection. There may be another wire named a neutral wire that makes the system a three phase, four-wire system.

What is meant by Thevenin’s theorem? Click Here!

The relation between Phase Voltage and Link Voltage of Star Connection

The system is considered as a balanced system. For a balanced-systems, an equal amount of current will pass through all 3-phase. That is why, R, Y, B has the same value of current. Now it has consequences. This uniform distribution of current makes the magnitudes of the voltages – E_NR, E_NY, E_NB same and they get displaced by 120 degrees from one another. 

In the above images, the arrow represents the direction of currents and voltages (not the actual order though). As we have discussed earlier, due to the uniform current distribution, the three arms’ voltage is equal so that we can write –

E_NR = E_NY = E_NB = _Eph.

And we can observe that the voltages in-between two lines is a two-phase voltage.

So, observing the NRYN loop, we can write that,

E_NR` + E<sub>RY</sub>` – E_NY` = 0

Or, E_RY` = E<sub>NY</sub>` – E_NR`

Now, from vector algebra,

E_RY = √ (E_NY² + E_NR² + 2 * E_NY * E_NR Cos60^o)

Or, E_L = √ (E_ph² + E_ph² + 2 * E_ph * E_ph x 0.5)

Or, E_L = √ (3E_ph²)

Or, E_l = √3 E_ph

In the same way, we can write, E_YB = E_NB – E_NY.

OR, E_L = √3 E_ph

And,

E_BR = E_NR – E_NB

Or, El = √3 Eph

So, we can say that the relation between the line voltage and phase voltage is:

Line Voltage = √3 x Phase voltage

What is Millman’s Theorem? Click Here!

Relation Between Phase Current and Line Current in Star Connection

The uniform current flow in phase windings is the similar as the current flow in the line conductor.

We can write –

I_R = I_NR

I_Y = I_NY

And I_B = I_NB

Now, the phase current will be –

I_NR = I_NY = I_NB = I_ph

And the line current will be – I_R = I_Y = I_B = I_L

So, we can say that, I_R = I_Y = I_B = I_L

What is Maximum Power Transfer Theorem? Click Here!

Delta connection

Delta connection is another method to establish three phases of an electrical system. The end terminal of the windings is attached to the starting of the other terminals. Three-line conductors are connected from three junctions. The delta connection is set up by tying the ends. For that we combine a₂ with b₁, b₂ with c₁ and c₂ with a₁. Line conductors are the R, Y, B which run from three junctions. The below image depicts a typical delta connection and shows the end-to-end connections.

The relation between phase voltage and the line voltage of the Delta connection

Let us find out the relation between phase voltage of a delta circuit with the circuit’s line voltage. For that, observe the above image carefully. We can say that the value of the voltage at both the terminal 1 and terminal 2 is the same as the terminal R and terminal Y.

So, we can write – E₁₂ = E_RY.

In the same way, we can conclude by observing the circuit, E₂₃ = E_YE.

And E₃₁ = E_BR

The phase voltages are written as: E₁₂ = E₂₃ = E₃₁ = E_ph

The line voltages are written as: E_RY = E_YB = E_BR = E_L.

So, we can conclude that, in case of a delta connection, the phase voltage will be equal to the circuit’s line voltage.

To know About Kirchhoff’s Laws: Click Here!

The relation between phase current and line current in delta connection

For a balanced delta connection, the constant voltage value affects the current values. The current values of I₁₂, I₂₃, I₃₁ are equal, but they are displaced by 120 degrees from one another. Observe the below-given phasor diagram.

We can write, I₁₂ = I₂₃ = I₃₁ = I_ph

Now, by applying Kirchhoff’s law at junction 1,

We know that the algebraic sum of the current of a node is zero.

So, I₃₁` = I<sub>R</sub>` + I₁₂`

The vectoral differences come as I_R` = I<sub>31</sub>` – I₁₂`

By applying vector algebra,

I_R = √ (I₃₁² + I₁₂² + 2 * I₃₁ * I₁₂ * Cos 60^o)

Or, I_R = √ (I_ph² + I_ph² + 2 * I_ph * I_ph x 0.5)

As, we have discussed earlier, I_R = I_L.

Or, I_L = √ (3I_ph²)

Or, I_L = √3 * I_ph

In the same way, I_Y` = I<sub>12</sub>` – I₂₃.`

Or, I_L = √ 3 * I_ph

And, I_B` = I<sub>23</sub>` – I₃₁`

Or, I_L = √ 3 I_ph

So, the relation between line current and phase current can be written as:

Line Current = √3 x Phase Current

Difference between Star and Delta Connection

Star and delta methods are two renowned methods for three phase systems. Depending on various factors, there are some fundamental differences between them. Let us discuss some of them.

POINTS OF COMPARISION	STAR CONNECTION	DELTA CONNECTION
Definition	The three terminals are allied at a common point. This type of circuit is called a Star connection.	Three end terminals of the circuits are connected with each other to form a closed loop known as delta connection.
Neutral Point	There is a neutral point in star connection.	No such neutral point exists in delta connection.
The relation between phase and line voltage	Line voltage is calculated as √three times of phase voltage for star connection.	Phase voltage and line voltages are equal to each other for delta connections.
The relation between phase current and line current	Phase current and line current for star connection is equal to each other.	Line current is √three times of phase current for delta connections.
Speed as starters	Star connected motors are usually slower as they get 1/√3 rd of the voltage.	Delta connected motors are usually faster as they get the full line voltage.
Phase Voltage	The value of phase voltage for a star connection is lower as they get just 1/√3 part of the line voltage.	The value of phase voltage is higher as phase voltage, and line voltages are equal.
Requirement of Insulation	Low level of insulation required for a star connection.	High level of insulation is required for delta connection.
Usage	Power transmission networks use a star connection.	Power distribution system uses a delta connection.
The number of turns required.	Star connection requires a lesser number of turns.	Delta connection requires a higher number of turns.
Received voltage	Every single winding receives 230 volts of voltage in star connection.	In delta connection, every single winding receives 414 volts of voltage.
Available systems	Star connection of three wire three phases and four wire three phase systems are available.	Delta connection of three wire three phase systems, and four-wire three phase systems are available.

Learn About Basics of AC Circuit: Click Here!

Star delta transformation

Conversion from Star to Delta and Delta to Star

A star network can be converted into a delta network, and a delta connected network can be converted into a star network if needed. Conversion of circuits is necessary to simplify the complicated course, and thus the calculation becomes more effortless.

Conversion from Star to Delta

In this conversion, a connected star network is replaced by its equivalent delta connected network. The star and replaced delta figure are given. Observe the equations.

The value of Z₁, Z₂, Z₃ is given in terms of Z_A, Z_B, Z_C.

Z₁ = (Z_A Z_B + Z_B Z_C + Z_C Z_A) / Z_C = Σ (Z_A Z_B) / Z_C

Z₂ = (Z_A Z_B + Z_B Z_C + Z_C Z_A) / Z_B = Σ (Z_A Z_B) / Z_B

Z₃ = (Z_A Z_B + Z_B Z_C + Z_C Z_A) / Z_A = Σ (Z_A Z_B) / Z_A

We can easily convert a connected star network into a delta connected if we know the star-connected network’s value.

Learn About Advanced AC Circuit: Click Here!

Conversion from Delta to star

In this conversion, a delta connected network is replaced by its equivalent star connected network. The delta and replaced star figure are given. Observe the equations.

The value of Z_A, Z_B, Z_C is given in terms of Z₁, Z₂, Z_3.

Z_A = (Z₁ Z₂) / (Z₁ + Z₂ + Z₃)

Z_B = (Z₂ Z₃) / (Z₁ + Z₂ + Z₃)

Z_C = (Z₁ Z₃) / (Z₁ + Z₂ + Z₃)

We can easily convert a delta connected network into a star connected if we know the value of the delta connected network.

Cover GIF by: GIPHY

Cover Image Credit – Rufustelestrat, San Diego Reflecting Pond, CC BY-SA 3.0

Points of Discussions

• Introduction to Millman’s Theorem
• Theory of Millman’s Theorem
• Applications of Millman’s Theorem
• Problem Solving Steps for Millman’s Theorem
• Explanation of Theories
• Solved Problems on Millman’s Theorem

Introduction to Millman’s Theorem

In the previous Advanced Electrical Circuit Analysis articles, we have discussed some of the fundamental theories like – Thevenin’s Theorem, Norton’s Theorem, Superposition Theorem, etc. We have also come to know the Maximum Power transfer theorem for finding out the maximum load resistance to drain full power. In this article, we will learn about another important and fundamental electrical analysis to deal with complex circuits, known as Millman’s theorem. We will discuss the theory, the process to solve the problems related to this theory, the applications of this theory and other important aspects.

Professor Jacob Millman first proved the theorem, and that is why it is named after him. This theory helps us to simplify the circuit. Thus, it becomes easier to analyze the circuit. This theorem is also known as “Parallel generator theorem”. Millman’s theorem is applied in courses to calculate the voltage of some specified circuitries. It is one of the essential theorems in Electrical Engineering.

What is meant by Thevenin’s theorem? Click Here!

Theory of Millman’s Theorem

Millman’s Theorem: It states that if multiple voltage sources (having internal resistances) are connected in parallel, this specific circuit can be replaced by a simpler circuit of a single voltage source and a resistance in series.

This theory helps us to find out voltages at the end of parallel branches if the circuit is structured in parallel connections. The principal aim of this theory is nothing but to reduce the complexity of the circuit.

Applications of Millman’s Theorem

Millman’s theorem is one of the efficient theorems. That is why there are several real-world applications for this theory. Millman’s theorem is applicable for a circuit with multiple voltage sources with their internal resistances in a parallelly connected way. It helps to solve complex circuit theory problems. Unbalanced bridges, parallel circuit problems can be solved using this theorem.

What are network theorems? Click Here!

Steps for Solving Problems regarding Millman’s Theorem

Generally, the given steps are tracked for solving Millman’s Theory problems. There are several other paths, but following these below-mentioned steps will lead to a more efficient result.

Step 1: Find out the conductance value of every single voltage source.

Step 2: Remove the load resistance. Calculate the equivalent conductance of the circuit.

Step 3: The circuit is now ready to apply Millman’s Theorem. Apply the theorem to find out the equivalent source voltage V. The below equation gives the V value.

V = (± V₁ G₁ ± V₂ G₂ ± V₃ G₃ ± … ±V_n G_n) / G₁ + G₂ + G₃ + … + G_n

V₁, V₂, V₃ are the voltages and G₁, G₂, G₃ are their respective conductance.

Step 4: Now, find out the equivalent series resistance of the circuit with the help of conductance value, calculated earlier. The equivalent series resistance is given by the expression: R = 1 / G

Step 5: At last, calculate the current through the load by the following equation.

I_L = V / (R + R_L)

Here, I_L is the current through the load resistance. R_L is the load resistance. R is the equivalent series resistance. V is the identical source voltage calculated with the help of conductance of their respective voltages.

What is Maximum Power Transfer Theorem? Click Here!

Explanation of Millman’s Theorem

To explain the theorem in details, let us take an example of a specified circuit. The below image describes the needed circuit. The picture shows a typical DC circuit with multiple parallel source voltages with their internal resistances and with the load resistance. RL gives the value of load resistance.

Let us assume that ‘I’ is the current value through the parallel current sources. G gives the equivalent conductance or admittance value. The resultant circuit is shown below.

I = I₁ + I₂ +I₃ + …

G = G₁ + G₂ + G₃ + ….

Now, the final current source is replaced by an equivalent source voltage. The voltage ‘V’ can be written as: V = 1/G = (± I₁ ± I₂ ± I₃ ± … ±I_n) / (G₁ +G₂ + G₃ + … + G_n)

And equivalent series resistance comes as:

R = 1 / G = 1 / (G₁ + G₂ + G₃ + … + G_n)

Now, we know that V = IR and R = 1 / G

So, V can be written as:

V = [± (V₁ / R₁) ± (V₂ / R₂) ± (V₃ / R₃) ± … ± (V_n / R_n)] / [ (1 / R₁) ± (1 / R₂) ± (1 / R₃) ± … ± (1 / R_n)]

R is the equivalent series resistance.

Now, as per Millman’s theory, the equivalent voltage source comes to be:

V = (± V₁ G₁ ± V₂ G₂ ± V₃ G₃ ± … ±V_n G_n) / (G₁ + G₂ + G₃ + … + G_n)

Or, V = Σ (n, k = 1) V_k G_k / Σ (n, k = 1) G_k

G_k = 1 /R_k

To know About Kirchhoff’s Laws: Click Here!

Solved Problems on Millman’s Theorem

1. A complex circuit is given below. Find the current through the 4 ohms resistance. Use Millman’s Theorem to solve the problem.

Solution: We will solve the problem by following the previously mentioned steps.

So, we have to find out the voltage value and the equivalent resistance value.

We know that the voltage is given by,

V = [± (V₁ / R₁) ± (V₂ / R₂) ± (V₃ / R₃) ± … ± (V_n / R_n)] / [ (1 / R₁) ± (1 / R₂) ± (1 / R₃) ± … ± (1 / R_n)]

Here, we have three voltage source and three resistances. So, the updated equation will be,

V_AB = [± (V₁ / R₁) ± (V₂ / R₂) ± (V₃ / R₃)] / [ (1 / R₁) ± (1 / R₂) ± (1 / R₃)]

V_AB = [(5 / 6) + (6 / 4) + (4 / 2)] / [(1 / 6) + (1 / 4) + (1 / 2)]

V_AB = 4.33 / 0.9167

OR, V_AB = 4.727 V

Now, we have to calculate the equivalent resistance of the circuit, or the Thevenin’s equivalent resistance is Rth.

R_TH = [(1 / 6) + (1 / 4) + (1 / 2)] ^-1

Or, R_TH = 1.09 ohms

At the last step, we will find out the current value through the load resistance, that is 4 ohms.

We know that, I_L = V_AB / (R_TH + R_L)

Or, I_L = 4.727 / (1.09 + 4)

Or, I_L = 4.727 / 5.09

Or, I_L = 0.9287 A

So, The load current through 4 ohms load is 0.9287 A.

Learn About Basics of AC Circuit: Click Here!

2. A complex electrical circuit is given below.  Find out the current through the 16 ohms load resistance. Use Millman’s theorem to solve the problems.

Solution: We will solve the problem by following the previously mentioned steps.

At first, we have to calculate the current value using Norton’s theorem.

The current ‘I’ can be written as: I = I₁ + I₂ + I₃

Or, I = 10 + 6 – 8

Or, I = 8 A

Now we have to find out the Equivalent resistance value. We represent the equivalent resistances of R₁, R₂, R₃ as R_N.

So, R_N = [(1 / R₁) + (1 / R₂) + (1 / R₃)]^-1

Or, R_N = [(1/ 24) + (1 / 8) + (1 / 12)]^-1

Or, R_N = 4 ohms

We now redraw the circuit with equivalent voltage and resistances value and place the circuit’s load resistance.

At the last step, we have to find out the load Current. So, I_L = I x R / (R + R_L)

Or, I_L = 8 x 4 / (4 + 16)

Or, I_L = 1.6 A.

So, the load current through the 8 ohms load resistor is 1.6 A.

Learn About Advanced AC Circuit: Click Here!

3. A complex AC network is given below.  Compute the current passing through the Load ZL. Use Millman’s Theorem to solve the problem.

Solution: We will solve the problem by following the previously mentioned steps. In this problem, we can see that a current source is given. But we know that we cannot apply Millman’s Theory for a current source. So, It is possible to  convert the current source to a voltage source.

Now, we apply Millman’s theorem and finds out the equivalent voltage.

We know that,

V = [± (V₁ / R₁) ± (V₂ / R₂) ± (V₃ / R₃)] / [ (1 / R₁) ± (1 / R₂) ± (1 / R₃)]

So, V = (1 * 1 ∠0^o + 1 * 5 ∠0^o + 0.2 * 25 ∠0^o) / ( 1 + 1 + 0.2)

Or, V = 11 / 2.2 = 5 ∠0^o V.

I_L gives the current through the load resistance.

As we know, V = IR.

Or, I_L = V / Z_L = 5 ∠0^o / (2 + j4)

Or, I_L = 1.12 ∠-63.43^o A.

So, Current through the load resistance is 1.12 ∠-63.43^o A.  

Cover Photo By: Abyss