Velocity

How to Find Tangential Velocity: Several Insights and Problem Examples

January 21, 2024January 6, 2022 by Keerthana Srikumar

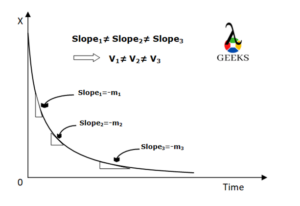
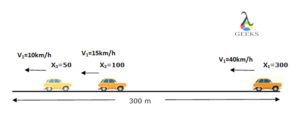
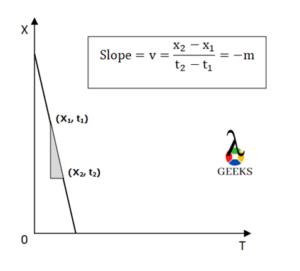
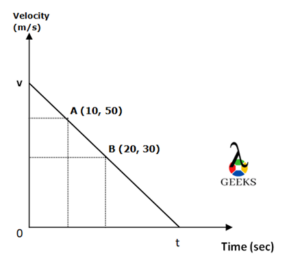
Tangential velocity is a crucial concept in physics that helps us understand the speed and direction of an object moving in a circular path. It provides valuable information about the object’s motion and is used in various scientific and engineering applications. In this blog post, we will explore how to find tangential velocity, including the formulas, calculations, and practical applications associated with it.

How to Calculate Tangential Velocity

The Formula to Calculate Tangential Velocity

To calculate the tangential velocity of an object moving in a circular path, we can use the formula:

$V_{t} = r cdot omega$

where $V_{t}$ represents the tangential velocity, $r$ is the radius of the circular path, and $omega$ stands for the angular velocity of the object.

Calculating Tangential Velocity from Angular Velocity

Image by MikeRun – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

If we know the angular velocity of an object in radians per second, we can calculate the tangential velocity using the formula mentioned earlier. Let’s consider an example to illustrate this concept:

Example: A car’s tire has an angular velocity of 5 radians per second, and its radius is 0.4 meters. What is the tangential velocity of the car?

Solution: Using the formula $V_{t} = r cdot omega$ , we substitute the given values:

$V_{t} = 0.4 , text{m} cdot 5 , text{rad/s} = 2 , text{m/s}$

Therefore, the tangential velocity of the car is 2 m/s.

Calculating Tangential Velocity without Time

In some cases, we might not be given the time it takes for an object to complete one revolution. However, if we know the distance traveled by the object in the circular path, we can still calculate the tangential velocity using the formula:

$V_{t} = frac{s}{t}$

where $s$ represents the distance traveled and $t$ is the time taken.

Example: A cyclist completes one lap around a circular track with a circumference of 100 meters in 20 seconds. What is the tangential velocity of the cyclist?

Solution: We can use the formula $V_{t} = frac{s}{t}$ , where $s = 100 , text{m}$ and $t = 20 , text{s}$ :

$V_{t} = frac{100 , text{m}}{20 , text{s}} = 5 , text{m/s}$

Therefore, the tangential velocity of the cyclist is 5 m/s.

Calculating Tangential Velocity without Radius

In certain situations, we may not have the radius of the circular path, but we might know the centripetal acceleration of the object. In such cases, we can determine the tangential velocity using the formula:

$V_{t} = sqrt{a cdot r}$

where $a$ represents the centripetal acceleration.

Example: An object is moving in a circular path with a centripetal acceleration of 10 m/s². If the radius of the circular path is 2 meters, what is the tangential velocity of the object?

Solution: Using the formula $V_{t} = sqrt{a cdot r}$ , we substitute the given values:

$V_{t} = sqrt{10 , text{m/s²} cdot 2 , text{m}} = sqrt{20 , text{m²/s²}}$

Simplifying the expression, we find $V_{t} approx 4.47 , text{m/s}$

Therefore, the tangential velocity of the object is approximately 4.47 m/s.

Practical Applications of Tangential Velocity

Image by MikeRun – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

Finding Tangential Velocity of Planets and Stars

Tangential velocity plays a crucial role in celestial mechanics, helping us determine the speed at which planets and stars move in their orbits. By studying the tangential velocities of celestial objects, scientists can gain insights into their orbital dynamics, understand the gravitational forces acting upon them, and make predictions about their future positions.

Finding Tangential Velocity of a Point or Particle

In particle physics or fluid dynamics, determining the tangential velocity of a point or particle is vital to understanding the motion of fluids or the behavior of particles within a system. This information helps scientists analyze the speed and direction of fluid flow, study the trajectories of particles, and predict the behavior of complex systems.

Tangential Velocity in Physics and its Relevance

Tangential velocity is a fundamental concept in physics, particularly in the study of rotational motion. It provides insights into the speed and direction of objects moving in circular paths or undergoing rotation. Understanding tangential velocity is critical in various fields, including mechanics, engineering, and astrophysics.

Worked Out Examples

Example of Calculating Tangential Velocity with Centripetal Acceleration

Suppose an object moves in a circular path with a centripetal acceleration of 6 m/s². If the radius of the circular path is 3 meters, what is the tangential velocity of the object?

Solution: Using the formula $V_{t} = sqrt{a cdot r}$ , we substitute the given values:

$V_{t} = sqrt{6 , text{m/s²} cdot 3 , text{m}} = sqrt{18 , text{m²/s²}}$

Simplifying the expression, we find $V_{t} approx 4.24 , text{m/s}$

Therefore, the tangential velocity of the object is approximately 4.24 m/s.

Example of Calculating Tangential Velocity Given Angular Acceleration

Imagine a wheel undergoes angular acceleration at a rate of 2 radians per second². If the radius of the wheel is 0.5 meters, what is the tangential velocity of a point on the wheel after 4 seconds?

Solution: We can start by calculating the angular velocity using the formula $omega = alpha cdot t$ , where $alpha$ represents the angular acceleration and $t$ is the time:

$omega = 2 , text{rad/s²} cdot 4 , text{s} = 8 , text{rad/s}$

Next, we can use the formula $V_{t} = r cdot omega$ to find the tangential velocity:

$V_{t} = 0.5 , text{m} cdot 8 , text{rad/s} = 4 , text{m/s}$

Therefore, the tangential velocity of the point on the wheel after 4 seconds is 4 m/s.

Example of Calculating Tangential Velocity from RPM

Let’s consider a scenario where a wheel has a rotational speed of 120 revolutions per minute (RPM). If the radius of the wheel is 0.3 meters, what is the tangential velocity of a point on the wheel?

Solution: We start by converting the rotational speed from RPM to radians per second. Since one revolution is equal to $2pi$ radians, we can use the conversion factor:

$text{Rotational speed in radians per second} = frac{text{Rotational speed in RPM} cdot 2pi}{60}$

In this case, the rotational speed in radians per second would be:

$frac{120 cdot 2pi}{60} = 4pi , text{rad/s}$

Next, we can use the formula $V_{t} = r cdot omega$ to find the tangential velocity:

$V_{t} = 0.3 , text{m} cdot 4pi , text{rad/s} = 1.2pi , text{m/s}$

Therefore, the tangential velocity of a point on the wheel is approximately $1.2pi , text{m/s}$ .

Understanding how to find tangential velocity is essential for comprehending the motion of objects in circular paths or undergoing rotation. By applying the formulas and calculations discussed in this blog post, you can determine the tangential velocity of various objects and gain insights into their speed and direction. Tangential velocity plays a significant role in physics, engineering, and other scientific disciplines, enabling us to analyze and predict the behavior of complex systems.

How do I find the tangential velocity of a projectile and its intersection with the concept of finding horizontal velocity of a projectile?

To find the tangential velocity of a projectile, one must consider the horizontal velocity and the vertical velocity component. The tangential velocity represents the rate at which the projectile moves along its curved path. By analyzing the concept of finding horizontal velocity of a projectile, we can determine the initial velocity of the projectile along the horizontal axis. This initial velocity plays a crucial role in determining the tangential velocity of the projectile. For a detailed explanation on how to find the horizontal velocity of a projectile, refer to the article Finding Horizontal Velocity of a Projectile.

Numerical Problems on how to find tangential velocity

Problem 1:

An object is moving in a circular path with a radius of 5 meters. The object completes one full revolution in 10 seconds. Find the tangential velocity of the object.

Solution:

Given:
Radius of the circular path, r = 5 m
Time taken to complete one revolution, T = 10 s

The formula for tangential velocity is given by:
$v = frac{{2 pi r}}{{T}}$

Substituting the given values into the formula:
$v = frac{{2 pi cdot 5}}{{10}}$

Simplifying:
$v = frac{{10 pi}}{{10}}$

Final Answer:
$v = pi , text{m/s}$

Problem 2:

A car is moving in a circular track with a radius of 100 meters. The car completes one full revolution in 50 seconds. Determine the tangential velocity of the car.

Solution:

Given:
Radius of the circular track, r = 100 m
Time taken to complete one revolution, T = 50 s

Using the formula for tangential velocity:
$v = frac{{2 pi r}}{{T}}$

Substituting the given values into the formula:
$v = frac{{2 pi cdot 100}}{{50}}$

Simplifying:
$v = frac{{200 pi}}{{50}}$

Final Answer:
$v = 4pi , text{m/s}$

Problem 3:

A Ferris wheel has a radius of 20 meters and completes one full revolution in 60 seconds. Determine the tangential velocity of a person sitting on the Ferris wheel.

Solution:

Given:
Radius of the Ferris wheel, r = 20 m
Time taken to complete one revolution, T = 60 s

Using the formula for tangential velocity:
$v = frac{{2 pi r}}{{T}}$

Substituting the given values into the formula:
$v = frac{{2 pi cdot 20}}{{60}}$

Simplifying:
$v = frac{{40 pi}}{{60}}$

Final Answer:
$v = frac{{2 pi}}{{3}} , text{m/s}$

Also Read:

Negative Velocity Graph: Different Graphs And Their Explanations

January 21, 2024January 5, 2022 by AKSHITA MAPARI

In this article, we are going to discuss negative velocity along with graphs and solve problems to understand various facts of negative velocity.

If the velocity of an object decreases with respect to time duration then the object is said to have a negative velocity that might be constant, varying, instantaneous, or relative to the direction of the velocity of some other object into consideration.

Constant Negative Velocity Graph

If the slope of the position v/s time graph is negative and the distance decreases at a constant rate along with time, then it is said to be a constant negative velocity graph.

If ‘m’ is a value equal to the slope of the graph, which is linear and remains the same on calculating the slope between any two points on the line then the velocity is constant. Since the distance abates with time, the slope is negative and hence the velocity is negative.

Problem 1: Consider a pulley ties with two masses on both the ends of the rope of length 30meters, the mass on one end of the rope is pulled to raise another mass tied on another end of the rope at a constant rate. If 10meters of the rope was pulled in the first 12seconds and 20meters of ropes in the next 24seconds, then calculate the velocity of the mass tied on another end.

Solution: Since the change in length of the rope on one side in 12seconds is from say 0 to 10 meters and at the same time length of the rope has decreased to 30-10=20meters on another end of the rope.

Now the length of the rope is 20meters, so, after pulling 20meters of rope in 24seconds, the length of the rope on the other side is 20-20=0meters.

Hence, we have: x₁=30m, x₂=20m and x₃=0

Time t₁=0, t₂=12 seconds, t₃=12+24=36seconds

Therefore,

Slope₁=x₂-x₁/t₂-t₁=20-30/12-0=-10/12=-0.8m/s

Slope₂=x₃-x₂/t₃-t₂=0-20/36-12=-20/24=-0.8m/s

Slope₃=x₃-x₁/t₃-t₁=0-30/36-0=-30/36=-10/12=-0.8m/s

It is clear that

Slope₁=Slope₂=Slope₃=-0.8m/s

Hence the slope is linear and has constant negative velocity.

Negative Uniform Velocity Graph

When the object covers equal distance in equal intervals of time then the object is said to have uniform velocity, and if the object traverses back in a uniform velocity then the object is moving with negative uniform velocity.

negative velocity graph — **Negative Uniform Velocity Graph**

As the object displaces an equal distance in an equal interval of time, it implies that the velocity of the object is constant and hence there is no acceleration of the object.

Problem 2: Supposed, a narrow road runs from a village from point A to B such that only one car can travel on the road at a time. The length of the narrow road is 1km long. A carA travels a distance of 300meters from a narrow road from point A and encounters carB, hence starts reversing back at a constant speed and covers 3meters per second. Plot a graph and find the velocity at 3 different points.

Solution: The displacement of the car is 3meters per second and the distance from pointA decreases at the rate of 3m/s. A CarA had covered a distance of 300meters and will traverse back 300meters at a rate of 3m/s.

Position(x meters)	Time(t sec)
300	0
297	1
294	2
291	3
288	4
285	5

Table showing position of an object varied with time

We plot a graph for displacement v/s time,

Slope₁=x₂-x₁/t₂-t₁=294-297/2-1=-3/1=-3m/s

Slope₂=x₃-x₂/t₃-t₂=291-294/3-2=-3/1=-3m/s

Slope₃=x₃-x₁/t₃-t₁=288-291/4-3=-3/1=-3m/s

Slope₁= Slope₂= Slope₃=-3 m/s

The slope is constant and negative, and hence the velocity of the car taking a reverse on a narrow road is -3m/s.

Negative Relative Velocity Graph

Velocity is a vector quantity and relative velocity is a vector difference of velocities of two bodies. That is if the velocity of object A is V_a and that of object B is moving with velocity V_b, then the relative velocity of both the objects with respect to each other is V_ab=V_a-V_b.

On finding the slope of position v/s time plot, we can calculate the relative velocity of the object with respect to each other. If both the objects are decelerating then the slope of the graph will be negative.

Problem 3: A car traveling with a velocity of 60km/hr crosses a woman walking on a street with a speed of 2m/s in the same direction. What is their relative speed?

Solution: V₁=60 km/h=60*1000/60*60=16.67m/s

V₂=2m/s

Hence, the relative velocity of the car with respect to a lady is

V=V₁-V₂=60-2=58m/s

The relative velocity of the car will be 58m/s and that of the woman will be –58m/s as the speed of a car is faster than the woman.

Negative Velocity Positive Acceleration Graph

If the object accelerates back from its original position along with time by changing the velocity of the object then we have negative velocity but the acceleration of the object is positive.

The object accelerating backward changes its velocity frequently, that is the rate of displacement of the object in a time interval is not constant and hence the graph shows different slopes on plotting the position of the object at different times.

If the velocity of the object decreases at an exponential rate then we get the positive acceleration from the negative velocity of the object. Let us illustrate this with the problem below.

Problem 4: Consider the same situation given in problem No.2 and the same car is accelerating backward decreasing its speed. Suppose the covers first 200 meters with a speed of 40 km/h and next 50 meters with a speed of 15 km/h and remaining distance in 10 km/h speed. Then calculate the velocity and acceleration of the car at different points.

Solution: A car initially was at say point X₁= 300 and travels 200 meters to reach point X₂= 100 with velocity V₁=40 km/h. From where the velocity of the car changes to V₂=15 km/h and travels next 50 meters and velocity slightly drop to 10 km/h and comes at the original position on traveling 50 meters on the same speed.

**A Car accelerating in Reverse Direction**

The time taken to elapse 200 meters with the speed of 40 km/h is

t₁=Distance/Speed=200*60*60/40*1000=18 seconds

Time taken to cover 50 meters with a speed of 15 km/h is

t₂=Distance/Speed=50*60*60/15*1000=12 seconds

And a time taken to cover a distance of 50 meters with a speed of 10 km/h is

t₃=Distance/Speed=50* 60*60/10*1000=18 seconds

Therefore, T₁=18 seconds, T₂=18+12=30 seconds, T₃=30+18=48 seconds

Since the acceleration is define as the change in the velocity of a car in different time intervals, hence,

a₁=v₂-v₁/Time Interval=40-15/18=25*1000/18*60* 60=0.38 m/s²

a₂=v₂-v₁/Time Interval=15-10/12=5*1000/12*60*60=0.12 m/s²

a₃=v₂-v₁/Time Interval=10-0/18=10*1000/18*60*60=0.15 m/s²

This gives the positive acceleration. At the steeper slope of graph, the acceleration is of a car is higher and at gentle slope the acceleration is smaller.

Instantaneous Velocity Negative Graph

The object is said to have an instantaneous velocity when it displaces from its place drastically. If the displacement is in a reverse direction then it is said to have instantaneous negative velocity.

Here, the displacement of the object is seen suddenly in a short span of time and hence the instantaneous velocity is high.

This is seen in the case of spring tied with a mass at one end having its own potential and another end of the spring is held fixed on the rigid wall. When the mass is pulled away from the spring, the spring potential energy is built and the spring force pulls back the mass towards it to regain its original size by converting this potential energy into kinetic energy.

If the mass is heavy, then after releasing the mass attached to the spring, the spring force displaces the mass towards the rigid wall. The mass will resist the spring force and makes its place there. Hence, the position of the mass varied, and the distance separating it from the rigid wall decreased.

Since the displacement decreases, we have negative velocity in the picture.

Problem 5: If the mass of 2kg is attached to a string of length 1.5 meters at one end and another end is fixed at a rigid wall. On pulling the 50 cms away from its position linearly and released, the mass displaces towards the wall and remains stable at 80 cm away from the wall. Find the instantaneous velocity of the mass if the mass came to its resting position in 1 second.

Solution: A mass is displaced 150 – 80 =70cms =0.7m from its original position and has covered a distance of 70+50 =120cms =1.2m on releasing the spring.

Instantaneous velocity =Displacement/Time taken=1.2 m/1 second=1.2 m/s

Hence, the mass is displaced with a velocity of 1.2 m/s.

Negative Velocity v/s Time Graph Displacement

The velocity is a ratio displacement in a specific time duration, given by the relation

Velocity=Displacement/Time

Hence, the displacement of an object in time ‘t’ moving with velocity ‘v’ is

x=vt

The displacement of the object at a point or at a certain time can be calculated by multiplying it with the velocity of the object at that time.

Problem 6: Based on the following graph calculate the distance between points A & B.

Solution: Distance of Point A from the origin is

x₁=v₁t₁=10* 50=500m

The distance between point B and the origin is

x₂=v₂t₂=20*30=600m

Hence, the distance between point A & point B is

x=x₂-x₁=600-500=100m

Therefore, point B is 100 meters away from point A.

Read More on Negative Refraction.

Negative Slope Velocity Time Graph

The slope of the velocity-time graph will be negative only when the velocity of an object traveling decreases along with time.

If the slope of the velocity-time graph is negative, it means the acceleration is negative.

Problem 7: Find the average acceleration of a swing whose velocity is decreased with time as shown in the table.

Velocity(m/s)	Time(seconds)
8	1
6	5
4	10
2	15

Solution: Let’s calculate the acceleration at different time intervals

a1=v₂-v₁/t₂-t₁=4-8/10-1=-4/9=0.44 m/s²

a2=v₂-v₁/t₂-t₁=2-6/15-5=-4/10=0.40 m/s²

a3=v₂-v₁/t₂-t₁=6-8/5-1=-2/4=0.5 m/s²

a4=v₂-v₁/t₂-t₁=4-6/10-5=-2/5=0.40 m/s²

Hence, the average acceleration is

aˉ=a₁+a₂+a₃+a₄/4

aˉ=0.44+0.4+0.5+0.4/4=0.435 m/s²

Negative Displacement Velocity Time Graph

If the object is taking a reverse turn from its original position with decreasing velocity along with time then we get negative displacement velocity on plotting the same on a graph. The same is demonstrated in the graph below.

Since the velocity of the object is equal to the displacement of the object it makes in time duration, the displacement can be calculated as a product of the velocity of the object into time.

Problem 8: Consider the above velocity-time graph; the object is decelerating with time. Based on the above graph calculate the displacement of the object at a time= 5 seconds.

Solution: AT time t=5seconds, v=-20 m/s.

Velocity =Displacement/Time

x=vt

x=-20*5=-100m

Hence the displacement of an object is -100 meters from origin.

How to Calculate Distance from Negative Velocity Time Graph?

Since the velocity of the object is determined by the distance it covers in a specific time, the displacement of the object is a product of its velocity into time.

Velocity =Displacement/Time

x=vt

The displacement from the velocity-time graph is the area covered by the curves in the graph. For negative velocity the displacement will also be calculated and found to be negative, henceforth the displacement of the object with respect to its original position can be known.

Lets us see, how to calculate the displacement from the negative velocity-time graph through an example.

Problem 9: Consider the following velocity-time plot of an object, based on it calculate the displacement of an object and its position from its original position.

Solution: The area of the triangle in first quadrant is

Area of triangle =1/2 bh

x₁=1/2*10* 7=35m

The area of the triangle in fourth quadrant is

x₂=1/2*12* (-8)=-48m

Hence, the total displacement of an object is

x=x₁+x₂=35-48=-13m

This implies that the object has been displaced 13 meters further from the original position.

This is how the displacement is calculated from the velocity-time graph.

Frequently Asked Questions

How will you plot a graph from an object accelerating at a speed of 2m/s with its initial velocity of 4m/s?

Given: a=2m/s, u=4m/s

Velocity and time relation is given by the formula

v=u+at

At time t=0,

v=4+2*0=4m/s

At time t=1,

v=4+2* 1=4+2=6m/s

At time t=2,

v=4+2*2=4+4=8m/s

At time t=3,

v=4+2*3=4+6=10m/s

At time t=4,

v=4+2*4=4+8=12m/s

At time t=5,

v=4+2* 5=4+10=14m/s

Time(sec)	Velocity(m/s)
0	4
1	6
2	8
3	10
4	12
5	14

Plotting the graph of the same,

How to find acceleration from a velocity–time graph?

Acceleration is a rate of change of velocity at different time intervals.

Hence the slope of a graph of velocity v/s time will give the acceleration of the body.

Also Read:

How To Find Velocity With Acceleration: Different Approaches, Problems, Examples

January 21, 2024January 2, 2022 by AKSHITA MAPARI

Velocity and acceleration are fundamental concepts in physics that describe the motion of an object. Velocity measures the rate at which an object changes its position, while acceleration measures the rate at which an object changes its velocity. In this blog post, we will explore various methods to find velocity with acceleration, including calculating velocity with given acceleration and time, finding velocity with acceleration and initial velocity, determining velocity when acceleration is zero, and calculating velocity when acceleration is not constant. We will also delve into advanced concepts such as finding velocity with acceleration and displacement, distance, position, height, and radius. Let’s get started!

How to Calculate Velocity with Given Acceleration

Calculating Velocity with Acceleration and Time

When you know the acceleration of an object and the time for which it has been accelerating, you can calculate its velocity using the following formula:

$v = u + at$

Where:
– $v$ represents the final velocity
– $u$ represents the initial velocity
– $a$ represents the acceleration
– $t$ represents the time

To better understand this concept, let’s consider an example:

Example:
A car accelerates from rest with an acceleration of $2 , text{m/s}^2$ for a duration of $5 , text{s}$ . What is its final velocity?

First, we can denote the initial velocity as $u = 0 , text{m/s}$ since the car starts from rest. Using the formula mentioned above, we can calculate the final velocity:

$v = 0 + (2 , text{m/s}^2)(5 , text{s}) = 10 , text{m/s}$

Therefore, the car’s final velocity is $10 , text{m/s}$ .

Finding Velocity with Acceleration and Initial Velocity

In some cases, you may already know the initial velocity of an object along with its acceleration. To find the final velocity, you can use the following formula:

$v = u + at$

This formula is similar to the one mentioned earlier, but here the initial velocity is considered. Let’s take a look at an example to grasp this concept better:

Example:
A ball is thrown vertically upward with an initial velocity of $20 , text{m/s}$ . The acceleration due to gravity is $9.8 , text{m/s}^2$ . What is the ball’s final velocity when it reaches its maximum height?

In this case, we know the initial velocity $(u = 20 , text{m/s}$ ) and the acceleration $(a = -9.8 , text{m/s}^2$ since the ball is moving against gravity). We also know that the time it takes to reach the maximum height is unknown. However, at the maximum height, the ball comes to rest momentarily, which means the final velocity $(v$ ) is $0 , text{m/s}$ . Using the formula mentioned above, we can find the time it takes for the ball to reach the maximum height:

$0 = 20 , text{m/s} - (9.8 , text{m/s}^2)t$

Solving for $t$ , we find:

$t = frac{20 , text{m/s}}{9.8 , text{m/s}^2} approx 2.04 , text{s}$

Therefore, it takes approximately $2.04 , text{s}$ for the ball to reach its maximum height. The final velocity at the maximum height is $0 , text{m/s}$ .

Determining Velocity when Acceleration is Zero

When the acceleration of an object is zero, its velocity remains constant. This means that the object is either at rest or moving at a constant speed. In such cases, the final velocity $(v$ ) is equal to the initial velocity $(u$ ).

Let’s consider an example:

Example:
A car is moving at a constant speed of $30 , text{m/s}$ . What is its final velocity after $10 , text{s}$ ?

Since the car is moving at a constant speed, its acceleration is zero $(a = 0 , text{m/s}^2$ ). Therefore, the final velocity $(v$ ) is equal to the initial velocity $(u$ ):

$v = u = 30 , text{m/s}$

Hence, the car’s final velocity after $10 , text{s}$ is $30 , text{m/s}$ .

Calculating Velocity when Acceleration is Not Constant

In situations where acceleration is not constant, finding velocity requires integration or the use of more advanced techniques. However, in this blog post, we will not be going into the details of those methods. Instead, we will focus on the concept of constant acceleration, which simplifies the calculations.

Advanced Concepts in Finding Velocity with Acceleration

Finding Velocity with Acceleration and Displacement

When you know the initial velocity $(u$ ), acceleration $(a$ ), and displacement $(s$ ) of an object, you can find its final velocity $(v$ ) using the following formula:

$v^2 = u^2 + 2as$

Let’s consider an example to illustrate this concept:

Example:
A rocket traveling at $100 , text{m/s}$ undergoes an acceleration of $10 , text{m/s}^2$ over a distance of $500 , text{m}$ . What is the rocket’s final velocity?

Here, we know the initial velocity $(u = 100 , text{m/s}$ ), the acceleration $(a = 10 , text{m/s}^2$ ), and the displacement $(s = 500 , text{m}$ ). Using the formula mentioned above, we can calculate the final velocity $(v$ ):

$v^2 = (100 , text{m/s})^2 + 2(10 , text{m/s}^2)(500 , text{m})$

Simplifying the equation, we find:

$v^2 = 10000 , text{m}^2/text{s}^2 + 10000 , text{m}^2/text{s}^2$

$v^2 = 20000 , text{m}^2/text{s}^2$

Taking the square root of both sides, we get:

$v = sqrt{20000} , text{m/s} approx 141.42 , text{m/s}$

Therefore, the rocket’s final velocity is approximately $141.42 , text{m/s}$ .

Calculating Velocity with Acceleration and Distance

Similar to the previous concept, you can also find the final velocity $(v$ ) of an object by knowing its initial velocity $(u$ ), acceleration $(a$ ), and the distance traveled $(d$ ). The formula to use in this case is:

$v^2 = u^2 + 2ad$

Let’s work through an example to understand this concept better:

Example:
A skateboarder starts with an initial velocity of $5 , text{m/s}$ and accelerates at $2 , text{m/s}^2$ over a distance of $50 , text{m}$ . What is the skateboarder’s final velocity?

Given the initial velocity $(u = 5 , text{m/s}$ ), acceleration $(a = 2 , text{m/s}^2$ ), and distance $(d = 50 , text{m}$ ), we can use the formula to calculate the final velocity $(v$ ):

$v^2 = (5 , text{m/s})^2 + 2(2 , text{m/s}^2)(50 , text{m})$

Simplifying the equation, we get:

$v^2 = 25 , text{m}^2/text{s}^2 + 200 , text{m}^2/text{s}^2$

$v^2 = 225 , text{m}^2/text{s}^2$

Taking the square root of both sides, we find:

$v = sqrt{225} , text{m/s} = 15 , text{m/s}$

Hence, the skateboarder’s final velocity is $15 , text{m/s}$ .

Determining Velocity with Acceleration and Position

In certain scenarios, you might know the initial velocity $(u$ ), acceleration $(a$ ), and the position $(x$ ) of an object. To find the final velocity $(v$ ), you can use the following formula:

$v^2 = u^2 + 2ax$

Let’s consider an example to understand this concept better:

Example:
A train starts from rest and accelerates at $2 , text{m/s}^2$ to reach a position $x = 100 , text{m}$ . What is the train’s final velocity?

Here, we know the initial velocity $(u = 0 , text{m/s}$ ), acceleration $(a = 2 , text{m/s}^2$ ), and position $(x = 100 , text{m}$ ). Using the formula mentioned above, we can calculate the final velocity $(v$ ):

$v^2 = (0 , text{m/s})^2 + 2(2 , text{m/s}^2)(100 , text{m})$

Simplifying the equation, we find:

$v^2 = 0 , text{m}^2/text{s}^2 + 400 , text{m}^2/text{s}^2$

$v^2 = 400 , text{m}^2/text{s}^2$

Taking the square root of both sides, we get:

$v = sqrt{400} , text{m/s} = 20 , text{m/s}$

Therefore, the train’s final velocity is $20 , text{m/s}$ .

Calculating Velocity with Acceleration and Height

When dealing with vertical motion, such as objects falling or being thrown vertically, we can find the final velocity $(v$ ) by knowing the initial velocity $(u$ ), acceleration $(a$ ), and the height $(h$ ) of an object. The formula to use in this case is:

$v^2 - u^2 = 2ah$

Let’s work through an example to understand this concept better:

Example:
A ball is thrown vertically upward with an initial velocity of $10 , text{m/s}$ . The acceleration due to gravity is $9.8 , text{m/s}^2$ . What is the ball’s final velocity when it reaches a height of $20 , text{m}$ above the starting point?

Here, we know the initial velocity $(u = 10 , text{m/s}$ ), the acceleration $(a = -9.8 , text{m/s}^2$ since the ball is moving against gravity), and the height $(h = 20 , text{m}$ ). Using the formula mentioned above, we can calculate the final velocity $(v$ ):

$v^2 - (10 , text{m/s})^2 = 2(-9.8 , text{m/s}^2)(20 , text{m})$

Simplifying the equation, we find:

$v^2 - 100 , text{m}^2/text{s}^2 = -392 , text{m}^2/text{s}^2$

$v^2 = -292 , text{m}^2/text{s}^2 + 100 , text{m}^2/text{s}^2$

$v^2 = -192 , text{m}^2/text{s}^2$

Taking the square root of both sides, we get:

$v = sqrt{-192} , text{m/si}$

Since we cannot take the square root of a negative number in the real number system, this result is not physically meaningful. It indicates that the ball will not reach the specified height with the given initial velocity. Instead, it will fall back down before reaching that point.

Finding Velocity with Acceleration and Radius

When an object moves in a circular path with constant acceleration towards the center, such as in uniform circular motion, you can use the following formula to find its final velocity $(v$ ):

$v = sqrt{u^2 + 2ar}$

Where:
– $v$ represents the final velocity
– $u$ represents the initial velocity
– $a$ represents the acceleration
– $r$ represents the radius of the circular path

Let’s consider an example to illustrate this concept:

Example:
A car is moving along a circular track with a radius of $10 , text{m}$ . Its initial velocity is $5 , text{m/s}$ , and the acceleration towards the center is $2 , text{m/s}^2$ . What is the car’s final velocity?

Given the initial velocity $(u = 5 , text{m/s}$ ), the acceleration towards the center $(a = 2 , text{m/s}^2$ ), and the radius of the circular track $(r = 10 , text{m}$ ), we can use the formula mentioned above to calculate the final velocity $(v$ ):

$v = sqrt{(5 , text{m/s})^2 + 2(2 , text{m/s}^2)(10 , text{m})}$

Simplifying the equation, we find:

$v = sqrt{25 , text{m}^2/text{s}^2 + 40 , text{m}^2/text{s}^2}$

$v = sqrt{65 , text{m}^2/text{s}^2}$

Taking the square root of both sides, we get:

$v = sqrt{65} , text{m/s}$

Hence, the car’s final velocity is $sqrt{65} , text{m/s}$ .

Worked Out Examples

Now that we have explored various methods to find velocity with acceleration, let’s apply these concepts to some practical examples.

Example of Calculating Velocity with Given Acceleration and Time

Example:
A bicycle accelerates from rest with an acceleration of $2 , text{m/s}^2$ for a duration of $3 , text{s}$ . What is its final velocity?

Given:
$u = 0 , text{m/s}$ (initial velocity)
$a = 2 , text{m/s}^2$ (acceleration)
$t = 3 , text{s}$ (time)

To find the final velocity $(v$ ), we can use the formula:

$v = u + at$

Substituting the given values, we get:

$v = 0 + (2 , text{m/s}^2)(3 , text{s}) = 6 , text{m/s}$

Therefore, the bicycle’s final velocity is $6 , text{m/s}$ .

Example of Finding Velocity with Given Acceleration and Initial Velocity

Example:
A car is traveling at an initial velocity of $20 , text{m/s}$ and undergoes an acceleration of $2 , text{m/s}^2$ . What is its final velocity?

Given:
$u = 20 , text{m/s}$ (initial velocity)
$a = 2 , text{m/s}^2$ (acceleration)

To find the final velocity $(v$ ), we can use the formula:

$v = u + at$

However, we are not provided with the time $(t$ ) in this example. Therefore, we cannot directly calculate the final velocity. Additional information is required to solve this problem.

Example of Determining Velocity when Acceleration is Zero

Example:
A race car is moving on a straight track at a constant speed of $100 , text{m/s}$ . What is its final velocity after $10 , text{s}$ ?

Given:
$u = 100 , text{m/s}$ (initial velocity)
$a = 0 , text{m/s}^2$ (acceleration)
$t = 10 , text{s}$ (time)

Since the acceleration is zero $(a = 0 , text{m/s}^2$ ), the final velocity $(v$ ) is equal to the initial velocity $(u$ ). Therefore, the car’s final velocity after $10 , text{s}$ is $100 , text{m/s}$ .

Example of Calculating Velocity when Acceleration is Not Constant

Example:
A rocket is launched into space, and its acceleration changes over time. The acceleration function is given by $a(t) = 40t , text{m/s}^2$ , where $t$ represents time in seconds. If the rocket starts from rest $(u = 0 , text{m/s}$ ), what is its final velocity after $4 , text{s}$ ?

Given:
$u = 0 , text{m/s}$ (initial velocity)
$t = 4 , text{s}$ (time)

Since the acceleration is not constant, we cannot directly use the formula $v = u + at$ to find the final velocity. To determine the final velocity, we would need additional information about how the acceleration changes over time.

Example of Finding Velocity with Given Acceleration and Displacement

Example:
An object slides down a frictionless inclined plane with an acceleration of $3 , text{m/s}^2$ . If it covers a displacement of $50 , text{m}$ along the plane, what is its final velocity?

Given:
$a = 3 , text{m/s}^2$ (acceleration)
$s = 50 , text{m}$ (displacement)

To find the final velocity $(v$ ), we can use the formula:

$v^2 = u^2 + 2as$

However, we are not provided with the initial velocity $(u$ ) in this example. Therefore, we cannot directly calculate the final velocity. Additional information is required to solve this problem.

In this blog post, we explored various methods to find velocity with acceleration. We learned how to calculate velocity with given acceleration and time, find velocity with acceleration and initial velocity, determine velocity when acceleration is zero, and calculate velocity when acceleration is not constant. Additionally, we delved into advanced concepts such as finding velocity with acceleration and displacement, distance, position, height, and radius. By understanding these concepts and applying the appropriate formulas, we can accurately calculate an object’s velocity in different scenarios. Whether you’re solving physics problems or analyzing motion in real-world situations, knowing how to find velocity with acceleration is crucial.

How can the concepts of finding velocity with acceleration and mass be combined?

The combination of acceleration and mass plays a crucial role in calculating velocity. By understanding the relationship between these two variables, one can effectively determine an object’s velocity using the formula Calculating velocity using acceleration and mass. This article explores the intersection of these concepts and provides insights into how velocity can be determined by considering both acceleration and mass. It delves into the mathematical equations and principles involved in this calculation, providing a comprehensive understanding of the topic.

Numerical Problems on How to Find Velocity with Acceleration

Problem 1:

Image by Cdang – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

A car starts from rest and accelerates uniformly at a rate of $3 , text{m/s}^2$ for a duration of $5 , text{s}$ . Find the final velocity of the car.

Solution:

Given:
Initial velocity $(u) = 0 , text{m/s}$ ,
Acceleration $(a) = 3 , text{m/s}^2$ ,
Time $(t) = 5 , text{s}$ .

To find the final velocity $(v)$ , we can use the formula:

$v = u + at$

Substituting the given values, we have:

$v = 0 + 3 times 5$

Simplifying the expression, we get:

$v = 15 , text{m/s}$

Therefore, the final velocity of the car is $15 , text{m/s}$ .

Problem 2:

An object accelerates from a velocity of $4 , text{m/s}$ to a velocity of $12 , text{m/s}$ in a time duration of $6 , text{s}$ . Calculate the acceleration of the object.

Solution:

Given:
Initial velocity $(u) = 4 , text{m/s}$ ,
Final velocity $(v) = 12 , text{m/s}$ ,
Time $(t) = 6 , text{s}$ .

To find the acceleration $(a)$ , we can use the formula:

$a = frac{v - u}{t}$

Substituting the given values, we have:

$a = frac{12 - 4}{6}$

Simplifying the expression, we get:

$a = frac{8}{6} = frac{4}{3} , text{m/s}^2$

Therefore, the acceleration of the object is $frac{4}{3} , text{m/s}^2$ .

Problem 3:

A particle is moving with an initial velocity of $10 , text{m/s}$ and comes to rest after traveling a distance of $80 , text{m}$ with a uniform deceleration. Find the deceleration of the particle.

Solution:

Given:
Initial velocity $(u) = 10 , text{m/s}$ ,
Final velocity $(v) = 0 , text{m/s}$ ,
Distance $(s) = 80 , text{m}$ .

To find the deceleration $(a)$ , we can use the formula:

$v^2 = u^2 - 2as$

Substituting the given values, we have:

$0^2 = 10^2 - 2a times 80$

Simplifying the expression, we get:

$100 = 160a$

Dividing both sides by $160$ , we obtain:

$a = frac{100}{160} = frac{5}{8} , text{m/s}^2$

Therefore, the deceleration of the particle is $frac{5}{8} , text{m/s}^2$ .

Also Read:

How to Calculate Velocity Head: A Master Guide to Fluid Dynamics

June 25, 2024January 2, 2022 by Core SME lambdageeks.com

how to calculate velocity head master fluid dynamics

Summary Calculating the velocity head is a crucial aspect of fluid dynamics, as it represents the energy required to accelerate a fluid to a specific velocity. This comprehensive guide will delve into the theoretical foundations, formulas, and practical examples to help you master the art of velocity head calculation in fluid dynamics. Theoretical Foundations of … Read more

How To Find Velocity With Acceleration And Initial Velocity: Different Approaches, Problems, Examples

January 21, 2024December 31, 2021 by Raghavi Acharya

Understanding how to find velocity with acceleration and initial velocity is crucial in the field of physics. velocity is a fundamental concept that describes an object’s speed and direction of motion. acceleration, on the other hand, measures the rate at which an object changes its velocity. By combining the initial velocity and acceleration, we can determine the final velocity of an object. In this blog post, we will explore the mathematical relationship between velocity, acceleration, and initial velocity, learn how to calculate velocity using these parameters, discuss special cases, explore real-life applications, highlight common mistakes to avoid, and provide practical examples along the way.

The Mathematical Relationship between Velocity, Acceleration, and Initial Velocity

How To Find Velocity With Acceleration And Initial Velocity: Different Approaches, Problems, Examples 34

A. The Formula and its Explanation

To find the velocity of an object with acceleration and initial velocity, we can use the following formula:

$v = u + at$

Where:
– (v) represents the final velocity
– (u) represents the initial velocity
– (a) represents the acceleration
– (t) represents the time taken

This formula is derived from the equation of motion under constant acceleration, which states that the change in velocity $v - u$ is equal to the product of acceleration and time.

B. Importance of the Relationship in Physics

The relationship between velocity, acceleration, and initial velocity is crucial in various branches of physics. It allows us to understand and analyze the motion of objects, predict their future positions, and study the effects of forces acting upon them. By calculating velocity using acceleration and initial velocity, we can gather valuable insights into the behavior of objects in motion and make informed predictions about their trajectories.

How to Calculate Velocity with Acceleration and Initial Velocity

A. Step-by-Step Guide

To calculate velocity using acceleration and initial velocity, follow these steps:

Identify the given values:
Initial velocity ((u))
Acceleration ((a))
Time taken $t$
Substitute the given values into the formula:

$v = u + at$

Perform the necessary calculations, considering the units of measurement.

The result will be the final velocity $v$ of the object.

B. Worked out Examples

Let’s work through a few examples to solidify our understanding.

Example 1: A car starts from rest with an acceleration of 4 m/s². After 5 seconds, what is its final velocity?

Given:
(u = 0) m/s (initial velocity)
(a = 4) m/s² (acceleration)
(t = 5) s (time taken)

Using the formula (v = u + at), we substitute the given values:

$v = 0 + 4 \times 5$

Simplifying the equation, we find:

$v = 20$

m/s

Therefore, the final velocity of the car after 5 seconds is 20 m/s.

Example 2: A ball is thrown upwards with an initial velocity of 15 m/s. The ball experiences a constant acceleration due to gravity of -9.8 m/s². How long will it take for the ball to reach its highest point?

Given:
(u = 15) m/s (initial velocity)
(a = -9.8) m/s² (acceleration)
(v = 0) m/s (final velocity, at the highest point)

Using the formula (v = u + at), we substitute the given values:

$0 = 15 - 9.8t$

Simplifying the equation, we find:

$9.8t = 15$

$t = \frac{15}{9.8} \approx 1.53$

Therefore, it will take approximately 1.53 seconds for the ball to reach its highest point.

Special Cases in Finding Velocity with Acceleration and Initial Velocity

In certain scenarios, specific conditions affect the calculation of velocity using acceleration and initial velocity. Let’s explore these special cases:

A. When Acceleration is Zero

When the acceleration is zero, the object is said to be moving at a constant velocity. In this case, the formula to find the final velocity simplifies to:

$v = u$

This means that the final velocity is equal to the initial velocity in the absence of acceleration.

B. When Initial Velocity is Zero

If the initial velocity is zero, the object starts from rest. In this case, the formula to find the final velocity simplifies to:

$v = at$

This indicates that the final velocity is directly proportional to the acceleration and the time taken.

C. When Both Acceleration and Initial Velocity are Zero

When both the acceleration and initial velocity are zero, the object remains at rest. In this scenario, the final velocity is also zero.

Applications of Velocity, Acceleration, and Initial Velocity Calculations

The calculations involving velocity, acceleration, and initial velocity have numerous applications in various fields. Let’s explore a few practical examples:

A. In Everyday Life

Understanding the velocity of a moving vehicle helps us determine the time it takes to reach a particular destination.
Calculating the acceleration of a car allows us to evaluate its performance and fuel efficiency.
Determining the initial velocity of a projectile enables us to predict its range and trajectory.

B. In Scientific Research

Studying the velocity and acceleration of celestial objects helps astronomers understand their motion and behavior.
Analyzing the initial velocity and acceleration of particles in physics experiments aids in determining their energies and trajectories.

C. In Technological Innovations

Calculating the velocity and acceleration of vehicles plays a crucial role in the design and improvement of transportation systems.
Analyzing the initial velocities and accelerations of objects in engineering applications helps ensure safety and efficiency in various processes.

How can velocity be determined using both acceleration and height?

When it comes to finding velocity, there are different methods depending on the available information. The concept of finding velocity using acceleration and initial velocity is well-known, but what about incorporating height into the equation? Understanding how to find velocity with height is crucial, as it provides a comprehensive approach to calculating velocity in various scenarios. By combining the knowledge of acceleration and initial velocity with the impact of height, you can gain a deeper understanding of velocity dynamics. To explore this further, check out this informative guide on Finding velocity with height: a guide.

Common Mistakes to Avoid when Calculating Velocity with Acceleration and Initial Velocity

To ensure accurate calculations, it’s essential to avoid common mistakes that can lead to errors. Here are some common pitfalls to watch out for:

A. Incorrect Units

Always ensure that the units of velocity, acceleration, and time are consistent throughout the calculations. Mixing units can result in incorrect final velocity values.

B. Misinterpretation of Negative Values

When dealing with negative values for acceleration or initial velocity, it’s crucial to interpret their meaning correctly. Negative acceleration represents a decrease in velocity, while a negative initial velocity indicates motion in the opposite direction.

C. Ignoring the Direction of Motion

By being mindful of these common mistakes, we can ensure precise and meaningful calculations.

Also Read:

How To Find Velocity With Acceleration And Time:Different Approaches,Problems,Examples

January 21, 2024December 30, 2021 by Keerthi Murthi

How to Find Velocity with Acceleration and Time

Image by User:Stannered – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

how to find velocity with acceleration and time — Image by Kristoffer Lindskov Hansen, Michael Bachmann Nielsen and Caroline Ewertsen – Wikimedia Commons, Licensed under CC BY 4.0.

How To Find Velocity With Acceleration And Time:Different Approaches,Problems,Examples 39

velocity, acceleration, and time are fundamental concepts in physics that help us understand motion and how objects change their speed over time. In this blog post, we will explore how to find velocity using acceleration and time. We will cover the basic concepts, the relationship between velocity, acceleration, and time, different methods for calculating velocity, special cases, advanced concepts, and practical applications. So let’s dive in!

Understanding the Basic Concepts

Before we delve into velocity calculation, it’s essential to grasp the basic concepts involved.

Definition of Velocity: Velocity is the rate of change of an object’s position with respect to time. It tells us both the speed and direction of an object’s motion. Velocity is a vector quantity, meaning it has both magnitude (speed) and direction.
Understanding acceleration: acceleration is the rate at which an object’s velocity changes over time. It tells us how quickly an object is speeding up or slowing down, or changing its direction. Like velocity, acceleration is also a vector quantity.
The Role of Time in velocity Calculation: Time is a crucial factor in velocity calculation because it allows us to measure the duration of motion and determine how quickly an object’s velocity changes.

The Relationship between Velocity, Acceleration, and Time

To understand how velocity, acceleration, and time are related, we need to explore the underlying physics.

The Physics Behind Velocity and acceleration: According to Newton’s second law of motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. In mathematical terms, we can express this as

$a = F / m$

, where a is acceleration, F is the net force, and m is the mass of the object. The net force can be determined using Newton’s laws, and by knowing the mass and net force, we can calculate acceleration.

How time Affects velocity and acceleration: When an object experiences a constant acceleration over time, we can calculate its final velocity using the equation

$vf = vi + at$

, where vf is the final velocity, vi is the initial velocity, a is the acceleration, and t is the time. This equation shows that the final velocity depends on the initial velocity, the acceleration, and the time elapsed.

Calculating Velocity with Given Acceleration and Time

Now that we understand the relationship between velocity, acceleration, and time, let’s explore the different methods for calculating velocity.

A. The Formula for Finding velocity: The formula for finding velocity when given acceleration and time is

$vf = vi + at$

. This equation allows us to determine the final velocity of an object after a certain amount of time.

Explanation of the Velocity Formula: In the equation, vf represents the final velocity, vi represents the initial velocity, a represents the acceleration, and t represents the time. By plugging in the values for acceleration and time, we can find the final velocity.
Worked-out Examples Using the Formula: Let’s consider a few examples to better understand the calculation process.

Example 1: A car accelerates uniformly from rest at 5 m/s² for 10 seconds. What is its final velocity?

Solution: Using the equation

$vf = vi + at$

, we can substitute the values as follows:

vf = 0 + (5 m/s²)(10 s)

vf = 50 m/s

Therefore, the car’s final velocity is 50 m/s.

Example 2: A ball rolls down a hill with an initial velocity of 2 m/s and an acceleration of 3 m/s² for 5 seconds. What is its final velocity?

Solution: Using the same equation, we can calculate the final velocity:

vf = 2 m/s + (3 m/s²)(5 s)

vf = 17 m/s

The ball’s final velocity is 17 m/s.

B. Steps to Calculate velocity: To calculate velocity using the given acceleration and time, follow these steps:

Identify the given values: Note down the values for acceleration and time.
Substitute the values into the formula: Plug the acceleration and time values into the equation

$vf = vi + at$

.
Perform the calculation: Multiply the acceleration by the time and add the initial velocity to find the final velocity.
Round the answer: Round the final velocity to the appropriate number of significant figures or decimal places, depending on the context.

C. Common Mistakes to Avoid When Calculating velocity: When calculating velocity, be mindful of these common mistakes:

Forgetting to account for the initial velocity: Ensure that you include the initial velocity when using the formula

$vf = vi + at$

.
- Misinterpreting the signs of velocity and acceleration: Pay attention to the direction of the velocity and acceleration vectors. Positive and negative signs indicate different directions.
- Using the wrong units: Use consistent units for acceleration, time, and velocity. Check whether you need to convert the units before performing calculations.
How can you find the final velocity without using acceleration, and what is its significance?

The concept of finding the final velocity without using acceleration is explored in detail in the article on Finding final velocity without using acceleration. This method is useful when the acceleration is not known or is not constant. By using the equation that relates final velocity, initial velocity, and time, one can determine the final velocity of an object without requiring knowledge of its acceleration. This approach allows for the calculation of final velocity with only limited information, which can be beneficial in various physics and engineering applications.

Special Cases in Velocity Calculation

While the formula

$vf = vi + at$

is commonly used to calculate velocity, there are some special cases worth exploring.

A. Finding initial velocity with acceleration and time:

Sometimes, we may need to find the initial velocity when given the acceleration and time. Rearranging the equation

$vf = vi + at$

allows us to solve for the initial velocity as

$vi = vf - at$

.
1. Understanding Initial velocity: Initial velocity refers to the velocity of an object at the beginning of a motion or a specific time interval.
2. How to Calculate initial velocity: To calculate the initial velocity, subtract the product of acceleration and time from the final velocity using the equation
  
  $vi = vf - at$
  
  .
  
  B. Calculating final velocity with acceleration and time:
  
  In some scenarios, we may need to determine the final velocity when given the acceleration and time. The formula
  
  $vf = vi + at$
  
  can still be used to find the final velocity.
  1. Understanding Final velocity: Final velocity is the velocity of an object at the end of a motion or a specific time interval.
  2. Steps to Calculate final velocity: To calculate the final velocity, use the formula
    
    $vf = vi + at$
    
    and substitute the given values for acceleration and time.
    
    C. Determining Average velocity with Acceleration and time:
    
    Average velocity can be calculated when both initial and final velocities are known. It is the total displacement divided by the total time taken.
    1. What is Average velocity? Average velocity is the total displacement of an object divided by the total time taken.
    2. How to Calculate Average velocity: To calculate average velocity, use the formula
    $average velocity = (final velocity + initial velocity) / 2$
    
    .
    
    Advanced Concepts in Velocity Calculation
    
    Apart from the basic methods, there are advanced concepts worth exploring in velocity calculation.
    
    A. Finding Displacement with Velocity, Acceleration, and Time:
    
    Displacement is the change in position of an object. We can calculate displacement using the equation
    
    $displacement = (initial velocity x time) + (0.5 x acceleration x time²)$
    
    .
    1. Understanding Displacement: Displacement is a vector quantity that represents the change in position of an object in a particular direction.
    2. How to Calculate Displacement: Calculate displacement by multiplying the initial velocity by time, adding half the product of acceleration and time squared.
    B. Calculating Angular velocity with Angular Acceleration and Time:
    
    Angular velocity is the rate at which an object rotates around an axis. It can be calculated using the equation
    
    $angular velocity = initial angular velocity + (angular acceleration x time)$
    
    .
    1. What is Angular velocity? Angular velocity measures how quickly an object rotates about an axis.
    2. Steps to Calculate Angular velocity: To calculate angular velocity, add the product of angular acceleration and time to the initial angular velocity.
    Practical Applications of Velocity Calculation
    
    Velocity calculation has numerous practical applications in various fields, including physics, engineering, sports, and transportation.
    
    A. Real-life Examples of velocity Calculation:
    
    velocity calculation is used in real-life scenarios such as calculating the velocity of a moving car, determining the velocity of a projectile, or analyzing the speed of an athlete during a race.
    
    B. Importance of Velocity Calculation in Physics and Mathematics:
    
    Velocity calculation is fundamental in understanding the laws of motion, analyzing the behavior of moving objects, predicting outcomes, designing efficient systems, and solving complex mathematical problems.
    
    Also Read:

How To Find Final Velocity Without Acceleration: Facts, Problems, Examples

January 21, 2024December 30, 2021 by AKSHITA MAPARI

In this article, we are going to discuss how to find final velocity without acceleration along with some examples and facts.

Learn how to calculate an object’s final velocity using its initial speed, energy, position, and the forces acting upon it. Packed with practical examples and fascinating facts, this article is ideal for anyone eager to explore the nuances of physics beyond basic acceleration principles.

The velocity is defined as the ratio of displacement of the object upon the time interval given by the relation

Velocity=Displacement/Time

The velocity of the object can be calculated by measuring the total displacement of the object in a specific time interval.

Final velocity

Final velocity comes into the picture when the body has attained the maximum acceleration over a period of time. The acceleration is a difference between the final and the initial velocity of the object during the time.

Based on the motion of the body, whether it is in a planar motion, uniform circular motion, or in a projectile motion, the final velocity attained by the object can be calculated.

Final velocity of an Object in a Linear Motion

The object moving in a plane undergoes various external forces hence the velocity of the object may not be constant every time. The final velocity of the body does depend upon the initial velocity and how much is the velocity varying with time.

Calculate the Final velocity of an Object in a Linear Motion

Let us see the graph of velocity v/s time of the object accelerating in a uniform linear motion with initial velocity â€˜uâ€™ and chasing the final velocity of â€˜vâ€™.

For an object accelerating uniformly, if the initial velocity at time ( t = 0 ) is ( u ), and at a later time ( t ), the velocity increases to ( v ), then the acceleration of the object can be expressed as ( a = v – u ).

To calculate the total area of the plot in the given figure, it is equal to the combined area of the triangle (ΔABC) and the quadrilateral (ACDO).

Since,

v=x/t

x=vt

x = Area(ΔABC) + Area(ACDO)

=1/2 bh+lb

=1/2 t * (v-u)+ut

Since we are interested in finding the velocity without considering the acceleration term which is (v-u)

x=1/2 vt-1/2 ut+ut

x=1/2 vt+1/2 ut

2x=(v+u)t

2x/t=(v+u)

Therefore the final velocity of the object is

v=2x/t-u

On knowing the displacement of the object, the time taken for the displacement, and its initial velocity we can find out the final velocity picked up by the object.

Let us illustrate this with a simple example. Consider a car moving with a velocity of 20km/h starting from point A to reach point B. A car covers a distance of 60kms in 2 hours. What must be the final velocity of the car?

We know the initial velocity of the car u=20km/h,

Duration= 2hrs=120seconds

distance = 60 km

Using the formula derived above

v=2x/t-u=2*60/2-20=60-20=40km/h

Therefore the final velocity of the car will be 40kms/hr.

Projectile motion

An object in a projectile motion will lapse its path in a parabola. The initial and final velocity of the object will differ but the energy is conserved in a process. Initially, when the object is on the ground, it has more potential energy which is converted into kinetic energy for its flight.

Once reaching a particular height where all of its potential energy is transformed into kinetic energy, it falls freely on the ground converting this kinetic energy into potential energy. Hence the energy is conserved in a projectile motion of the object. That is, the sum of the kinetic and potential energy of the object before attaining maximum height is equal to the total energy after a flight.

If ‘u’ is the initial velocity and ‘v’ is the final velocity of an object with mass ‘m’, and ( h_0 ) is the initial height of the object from the ground, while ‘h’ is the highest height attained by the object in the air, then

K.E_initial+P.E_initial=K.E_final+P.E_final

1/2 mu²+mgh₀=1/2 mv²+mgh₁

Solving this equation further,

u²+2gh0=v²+2gh₁

v²=u²+2g(h₀-h₁)

v²=u²-2g(h₁-h₀)

Therefore the final velocity of the object in a projectile motion before it reaches the ground is

v = √(u² – 2g(h₁ – h₀))

The change in the velocity of the object in projectile motion is Δv = v – u.

Ponder upon the helicopter dropping food parcels to people in a flood-affected area. What will be the velocity of the food parcels dropped from the helicopter flying above at the height of 600m?

Of course, the initial velocity of the parcel will be zero before dropping it from the helicopter, i.e. u=0, and the height of the helicopter from above the ground is given h=600m. Let v be the final velocity of the food parcel when it is released from the helicopter.

Substituting in the equation below

v = √(u² – 2g(h₁ – h₀))

v = √(0² – 2 * 10 * (0 – 600))

v = √12000 = 109.54 m/s

Hence, t=600/109.54=5.47 seconds Â is the time required to reach the food parcel to the ground once it is dropped from the helicopter.

Read more on Projectile Motion.

Velocity of the object in a circular motion

An object moving in a circular motion exerts a centrifugal force and centripetal force which are equal and opposite in direction and is given by the relation

F_c=mv²/r

The velocity of the object is always perpendicular to both these forces directing outward from the circular path. Due to which the velocity is the change in displacement with respect to time.

If the initial velocity of an object with mass ‘m’ accelerating on a circular track with radius ‘r’ is ‘u’, and ‘v’ is the final velocity of the object, then the net force acting on the object is

F=F₂+F₂

=mv²/r+mu²/r

=m/r ( v²+u²)

(r/m) F=v²-u²

v²=u²+r/m F

Therefore the final velocity of the object accelerating in a circular path is

v = √(u² + r/m F)

Frequently Asked Questions

Q1.What is the final velocity of the ball accelerating downward on rising at the height of 5m from above the ground, if the mass of the ball is 500 grams? Consider the initial velocity of the ball to be 3m/s.

Given: m=500 grams

h₀=5m

h₁=0

The initial velocity of the ball u=3m/s

Since the motion of the ball is in a projectile motion, the final velocity of the ball is

v = √(u² – 2g(h₁ – h₀))

v = √(3² – 2 * 10 * (0 – 5))

v = √(9 + 100)

v = √109

v=10.44 m/s

It is evident that the speed of the ball accelerating down the ground increases due to the gravitational pull of the Earth on the objects surrounding it.

Q2.If an object moving with its initial velocity of 3 m/s suddenly accelerates and picks up the velocity of 10 m/s. How much distance will the object covers in 5 minutes?

The initial velocity of the object is u=3m/s

The final velocity of the object is v=10m/s

Duration t= 5 minutes= 5* 60=300 seconds

v=2x/t-u

10=2x/300-3

13*300=2x

2x=3900

therefore x=1950 m

x=1.95 km

In a duration of 5 minutes, the object will cover a distance of 1.95 km.

Q3. The distance from Ratan’s house to her school is 800 meters. She begins walking to school from her house at 7:45 AM with an initial velocity of 0.8 m/s. She needs to be at school 5 minutes before 8:00 AM, so she increases her walking speed and arrives on time. What was her final walking speed?

Given: d=800m,

t=10 min = 10*60 =600seconds

Initial walking speed u=0.8 m/s

Hence,

v=2x/t-u

v=2*800/600-0.8

v=8/3-0.8

v=8-2.4/3=5.6/3=1.87 m/s

Hence, the final walking speed of Ratan was 1.87 m/s.

Q4.What will be the velocity of the object of mass 30 kg moving with initial velocity 3m/s which accelerates at a rate of 4m/s on the application of force of 15N?

The final velocity of the object is equal to the sum of the initial velocity and acceleration with time.

Hence, the final velocity of the object is V_initial+V_accelerating= 3m/s+4m/s=7m/s

Also Read:

Instantaneous Velocity Vs Velocity: Comparative Analysis

January 21, 2024December 29, 2021 by Raghavi Acharya

We have come across the terms velocity and instantaneous velocity. In this post, we will study instantaneous velocity vs velocity.

In physical sciences, velocity is the calculation used to measure the change in position according to the time taken. Whereas instantaneous velocity is the term used to calculate the change in S for a certain or point of time. It is measured by the slope of the V-T graph.

Now let us look into the more comparative analysis of instantaneous velocity vs velocity.

Instantaneous velocity vs velocity

The velocity calculated for a crucial period is known to be instantaneous velocity. The table below gives some fundamental differences between instantaneous velocity vs velocity.

Parameters required for comparison	Instantaneous velocity	Velocity
Meaning	The instantaneous velocity of anybody or an object under motion can be measured by considering the specified time the velocity is to be calculated.	Velocity is generally given as the quantity used to find the object’s position change, taking into account the period interval.
Denoted by	V_INST	V
Nature of the quantity	It is well known physical vector quantity.	It is well known physical vector quantity.
SI Unit	Generally indicated by length/time, i.e., m/s	Generally indicated by length/time, i.e., m/s
Terms required in the calculation	It requires the limit of average velocity, or we can even use position change and time.	It requires only two essential terms that are displacement change and time.
Formula	V = V_INST = ds/dt Where, s = position/ displacement change T = particular time	V = s/t Where, s = position/ displacement change T = time
Features	It represents the object’s velocity at a specified time and the direction of the path traveled by that object.	It represents the object’s velocity and direction of the path traveled by that object.
Derivative of what terms	It is considered the derivative of displacement and specified time or limit of V_avg.	It is considered the derivative of a slight change in particle displacement and time.
Applications	To find the velocity at any time.	To know the fastness of the body with time.
Relation between each other	Instantaneous velocity is almost similar to V only difference is it is calculated at the crucial period.	Velocity is the general method to find the position change with time.
Examples	A boy skating on the street takes a rest for a certain period.	A vehicle moves at the same velocity from beginning to end till it reaches its destination.

Therefore, the points mentioned above are the critical differences of instantaneous velocity vs velocity.

Velocity: Insights and Facts

Velocity is the primary quantity used in mechanics to know the speediness of the object.

It is in general defined as the measure of changes that a position of the body undergoes in motion taking into consideration the time interval. It is even considered the derivative of a particle’s position/displacement/distance with a period.
It signifies both direction of route and the value of the magnitude of a particle under motion. It can be considered to be a vector.
It is measured in terms of length indicated by meter and time by t that is m/s.

Now let us know the essential insights of instantaneous velocity.

Instantaneous Velocity: Facts

Instantaneous velocity is the primary term quantity used in physics to measure the speediness of the body at a required interval.

It is in general defined as the measure of a limit of changes that a position of the body undergoes in motion taking into consideration the specific time interval.
It is even considered the limit of the average velocity, which is the derivative of the total change in position/displacement/distance of a particle with a total period.
It signifies both direction of route and the value of the magnitude of a particle under motion. It can be considered to be a physical vector quantity.
It is measured in terms of length indicated by meter and time by t that is m/s.

Now, let’s compare instantaneous velocity vs velocity that is the post’s primary focus.

Mention the primary difference between velocity and speed?

If we come across the nature of speed and velocity, we can quickly know their fundamental differences.

It is proved that speed is a physical scalar as it mentions only the rate of fastness of a particle in movement, i.e., it indicates magnitude. In contrast, velocity is proved as a physical vector that signifies the fastness and direction of the body’s route. It is the simple essential difference between speed and velocity.

Now let us look into the difference between V_inst and speed.

Mention the primary difference between instantaneous velocity and speed?

As we saw above similarly, If we come across the nature of speed and then V_inst, we can quickly know their fundamental differences.

It is proved from the theories that speed is a physical scalar as it mentions only the rate of quickness that a particle posses when it is under movement, i.e., it indicates magnitude. Whereas V is the value measured at a minimal period interval, and even the value obtained will be less when it is measured only at the required time, as it specifies both magnitude value and pathway, it is a vector.

So, these are some primary differences between speed and instantaneous velocity.

Mention the fundamental difference between average velocity and velocity?

The direct comparison of average velocity and velocity is given below.

Velocity and average velocities are the same. Velocity, in general, is specified as the position change concerning the period interval.
In contrast, average velocity is calculated or measured as the average taken to final and initial velocities of the particle for total motion with total time.
Both have the same SI unit and dimensions.

Now it’s time to know the nature of instantaneous velocity vs velocity.

Nature of velocity

The nature of velocity is nothing but to tell what type of physical quantity it belongs to and to describe its features.

As we learned above in the comparison between instantaneous velocity vs velocity, it is a physical vector quantity that includes both terms magnitude that gives the value of speediness of the particle under motion and even denotes the path through which the particle travels.
It is a primary quantity widely used in mechanics, an important branch of physical sciences.
It is calculated in terms of the distance of a particle’s absolute path or specific path with the time taken to reach the final point (m/s).

We now know about the nature of velocity to move on to the other aspect of this article: instantaneous velocity.

Nature of instantaneous velocity

Similarly, the nature of instantaneous velocity is nothing but to tell what type of physical quantity it belongs to and to describe its features.

As mentioned above, like velocity, even V_inst is a physical vector quantity that includes both terms magnitude and gives the value of speediness of certain things under motion and even denotes the path through which the particle travels.
It is a primary quantity widely used in mechanics, an important branch of physical sciences, to measure the precise value of velocity.
It is calculated in terms of the limit of a distance of the full path or specific path of a particle, with the time taken to reach a point will be almost equal to zero.

We learned about the nature of both instantaneous velocities vs velocity; now, let us study the available examples of velocity that can be seen around us.

Examples of instantaneous velocity vs velocity

There is a movement for each action. There will be some amount of velocity for every movement associated with it. So the points shown below are some general examples of velocity.

Playing with a tire
Race between two vehicles
Using a keypad
Reaching school

Playing with a tire

If you ever played with a car tire during your childhood, you must know how to move it simultaneously while running. In this example, you can measure the velocity by taking both the quantities displacement and time of the tire. If you want to know the velocity at some specific position and time and you must measure V_inst

Race between two vehicles

One of the common examples of instantaneous velocity vs velocity is while going on a trip in a big vehicle. Assume a race has been begun between the two vehicles. You want your vehicle to move forward than the other so that you can win the game. There will be fluctuation in velocity, position, and time of the vehicle’s movement in this case. As said above, you can calculate both velocity and instantaneous velocity according to your necessities.

Using a keypad

When an individual starts to type on a keypad, typing a long paragraph’s overall speed or velocity can be measured using the velocity formula. If you want to find the velocity of typing for any particular sentence with time, you can take into account instantaneous velocity.

Reaching school

Assume you are late to your school/office, and you start to walk fast initially and later begin to run. Here the position change, speed, and time of an individual can be found using the velocity formula and, at some particular point, can be measured using V_inst.

Therefore, the insights mentioned above are the direct and prominent comparison of instantaneous velocity vs velocity.

Frequently Asked Questions | FAQs

How are instantaneous velocity and speed related to one another?

Usually, instantaneous speed and V_inst are interrelated with one another.

In physical science, the term speed refers to the quickness or the rate of motion in which the body moves. In contrast, the V_inst represents the change of position for a particular or required second during the complete travel taken with a total period. Here S and V have the same value when we calculate using a formula, but these two only indicate direction.

What is the application of instantaneous velocity in real life?

Every day every second, we will be having a different kind of movement; a human cannot stay idle.

Sometimes it becomes necessary to measure how fast or quick the movement has occurred. For this reason, we can use velocity and average velocity. But this movement can have some irregularities that cannot be found out using these standard measures. Therefore, for this purpose, V_inst came into existence to find the tiny, precise details of the velocity of a particle.

Why does it sometimes become difficult to measure the instantaneous velocity?

As instantaneous velocity will be a small value, it won’t be easy sometimes to measure it.

Al the other types of velocity will be easy to calculate as they all have a very simple formula od d/t. But whereas in measuring the instantaneous velocity, we have to consider the value of the limit and then consider the time and then try to solve it using the calculus, which requires time. So compared to the measure of different velocities, V_inst is challenging to calculate.

Also Read:

Instantaneous Velocity Vs Acceleration: Comparative Analysis

January 21, 2024December 28, 2021 by Raghavi Acharya

We are already familiar with the terms velocity and acceleration. In this post, we will know instantaneous velocity vs acceleration facts.

Velocity and acceleration are interrelated with each other. Instantaneous velocity is the calculation of velocity at any particular period, and acceleration is defined as the rate of change Velocity(V) with consideration to a period. If we take the derivative of V_inst with t, then we get acceleration.

In this article, we will concentrate more on Instantaneous velocity vs acceleration in detail.

Instantaneous Velocity: Definition and Facts

The term velocity is used to indicate or measure the particle’s speed in a period.

We know that the significance of velocity and what it denotes. Now coming to the word instantaneous velocity, it denotes the increase or decrease in particle speed in a particular period, i.e., it shows the speed at a required instant of time.
It is measured along the path on which the particle moves in consideration.
The graph used to plot instantaneous velocity (V_inst) shows the change of speed, i.e., increase or decrease of a body.

Now let us know about the other necessary quantity that we will focus on instantaneous velocity vs acceleration.

Acceleration: Definition and Facts

Acceleration is another important term used in everyday physics.

Acceleration in physical sciences is one of the essential quantities without which the basic calculation of mechanics is not possible.
It is, in general, given as the calculation or derivative of the change of velocity of an object/body in motion following its time.
If we consider the acceleration from the beginning to the end of the movement, then it is called average acceleration.
If we consider acceleration(a) calculation at a particular time or period or taken as the limiting value of a_avg, then it is known as instantaneous acceleration (a_inst).

Now let us concentrate on the article’s main focus, instantaneous velocity vs acceleration.

Instantaneous Velocity vs Acceleration

Here we will study more about the insights and facts of Instantaneous velocity vs acceleration.

Parameters of Comparison	Instantaneous Velocity	Acceleration
Definition	It helps to measure the speed of a body along a specified route at any particular period t.	The term acceleration specifies the change in speed or velocity of a particle along the direction of path in an interval of time.
Terms used in the calculation	Displacement/ Position/ Distance and time.	Velocity/ Speed and time.
Nature of the quantity	It is a physical vector quantity.	It is a physical vector quantity.
Derivative of the terms	It is the derivative of both displacement/position with consideration to time.	It is the derivative of both changes in velocity/speed of the particle/object considering time.
Formula	Displacement/Time (d/t) = ds/dt	Velocity/Time (v/t) = dv/dt
Unit	Measured in m/s	Measured in m/s²
Features	It indicates the body’s speed with a specified time and direction of the route.	It indicates the change in the velocity for specific intervals.
Example	A dog is chasing a bone.	A man is participating in a hurdle race.

So, these are some prominent differences of instantaneous velocity vs acceleration.

Is instantaneous velocity a vector or a scalar physical quantity?

We have already known that instantaneous velocity or V is a primary vector of physical quantities.

In general, it is a term used to measure the change in position or displacement of a body under motion with time. From its definition, we can note that it consists of both directions, and it also gives the value of the magnitude that are essential features of a vector.

Now let’s focus on the following aspects of calculating this instantaneous velocity vs acceleration in detail.

How do you find instantaneous velocity on a graph?

We can find instantaneous velocity in various methods; we will know about one here.

We can measure the V_inst of a particle or body under a motion in a specified period with the help of a P-T graph. We must follow only the basic steps of plotting the values, indicating the axes, taking the slope, and drawing a tangent; after this, we get the required V_inst of a body.

It is time to learn about the nature of acceleration.

To Know more about instantaneous velocity check below,
How to calculate instantaneous velocity

Is acceleration a scalar or vector physical quantity?

Acceleration is a physical vector, but it can sometimes be a scalar.

As acceleration signifies both magnitude and direction, it is called a physical vector quantity. The acceleration depends on the nature of the dimension in which it occurs. For example, on a number line, acceleration is scalar, whereas in-plane coordinates or space is considered a physical vector quantity.

Now let us know how to find this acceleration on a graph.

Acceleration: Steps to find using a Velocity-time graph

One of the ways to find the value of the acceleration of a moving body is from the velocity-time graph.

After indicating the axes and plotting the required values on a velocity-time graph, we must take the slope for specific measurements. Here the slope is equal to the required acceleration of the object. Sometimes you can even use a formula to calculate this slope.

Now concentrate on the essential features of instantaneous velocity.

To know more about how to acceleration on graph, you can see below
How to plot Constant acceleration graph

Examples of instantaneous velocity vs acceleration in daily life

For every object’s motion, we can calculate instantaneous velocity and acceleration. Thus, we get many daily life examples of instantaneous velocity vs acceleration.

A kid running a marathon takes specific rest time for each destination. Here to know the change in position for each stage, we can use instantaneous velocity, and if we consider its speed/velocity, it is acceleration.

In tennis, the position of the ball changes for each hit. We can calculate the change in position for each interval using instantaneous velocity, and if it is a change in velocity, it is balls acceleration.

While shifting the materials, due to heavy baggage, we may sometimes change our posture or position of moving things. Here we can record the change in position with the help of instantaneous velocity, and if it is a change in velocity, then it is materials acceleration.

Therefore, these are some daily life examples of V.

Frequently asked questions| FAQs

Can we consider the instantaneous velocity as the same as an acceleration?

Both instantaneous velocity and acceleration are different quantities when compared to one another.

The rate of change of quantity, if calculated with time, then is taken as the derivatives of respective quantities. Here V is taken as the position measure with time, and acceleration is the derivative of the velocity change following time. From this instinct, we can tell that both are derivative and integral.

What is the definition of instantaneous velocity?

The definition of velocity is almost similar to instantaneous velocity with some critical changes.

It is taken as the limit of a V as the interval period almost tends towards zero. It is even known as the derivative of distance/displacement with the instant t that stands for time. The unit of measurement is taken in terms of length and time. It may be in meters, kilometers, minutes or seconds, etc.

What is the definition of acceleration?

The acceleration is measured as the double derivative of displacement and time.

The meaning of acceleration is to find out the change in velocity that is increasing, decreasing, or constant variation in velocity considering the respective time interval and the path.
It is a physical vector quantity and is a significant factor in measuring the changes in velocity.
It can also be measured on a V-T graph because, in this graph, the slope is equal to the necessary acceleration of the body in movement.

How do you find instantaneous velocity with the help of acceleration?

Both the quantities instantaneous velocity and acceleration are related to one another in one way or another.

We have already known in our previous articles about instantaneous velocity. It is the first derivative of displacement or position with time. If we consider only the derivative of velocity with time, it will be the second derivative of position and time. Therefore, if we consider Vinst at a particular time, then by taking its derivative, we can measure a=d→vdt.

Also Read:

How to Find Net Force with Mass and Velocity: Various Methods, Problems and Facts

January 21, 2024December 22, 2021 by Manish Naik

In the world of physics, understanding the concept of net force is crucial. net force is the sum of all the forces acting on an object, and it plays a significant role in determining the object’s motion. In this blog post, we will explore how to find net force using mass and velocity. We will delve into the relationship between force, mass, and velocity, learn the mathematical formula to calculate net force, discuss factors that affect net force calculation, and explore practical applications. So let’s dive in!

The Relationship between Force, Mass, and Velocity

How to Find Net Force with Mass and Velocity: Various Methods, Problems and Facts 59

A. The Role of Mass in Determining Net Force

mass is an essential factor when it comes to determining net force. It is a measure of an object’s inertia, or its resistance to changes in motion. According to Newton’s second law of motion, the net force acting on an object is directly proportional to its mass. In simpler terms, the larger the mass, the greater the force required to cause a change in its motion.

B. The Role of Velocity in Determining Net Force

velocity, on the other hand, is the measure of an object’s speed and direction. It also plays a role in determining net force. When an object is accelerating or decelerating, its velocity is changing. According to Newton’s second law, the net force acting on an object is directly proportional to the rate of change of its velocity. In other words, a greater change in velocity requires a larger net force.

C. The Interplay of Mass and Velocity in Net Force Calculation

Now that we know the individual roles of mass and velocity, we can understand how they interact to calculate net force. The equation for calculating net force is as follows:

$[F_{\text{net}} = m \cdot a$

]

In this equation,

$F_{\text{net}}$

represents the net force,

$m$

represents the mass of the object, and

$a$

represents the acceleration. If the object is not accelerating, the equation simplifies to:

$[F_{\text{net}} = 0$

]

This means that when an object is at rest or moving at a constant velocity, the net force acting on it is zero.

How to Calculate Net Force with Mass and Velocity

A. The Mathematical Formula

As mentioned earlier, the formula to calculate net force is

$F_{\text{net}} = m \cdot a$

. To find the net force, you need to know the mass of the object and the acceleration it is experiencing. The unit of force is Newtons (N), which can be obtained by multiplying the mass in kilograms (kg) by the acceleration in meters per second squared (m/s²).

B. Step-by-step Guide to Calculate Net Force

To calculate net force, follow these steps:

Identify the mass of the object in kilograms (kg).
Determine the acceleration of the object in meters per second squared (m/s²).
Multiply the mass by the acceleration to obtain the net force.

C. Worked-out Examples

Let’s work through a couple of examples to solidify our understanding.

Example 1:

A car with a mass of 1000 kg is accelerating at a rate of 5 m/s². What is the net force acting on the car?

Solution:

Using the formula

$F_{\text{net}} = m \cdot a$

, we can substitute the given values:

$F_{\text{net}} = 1000 \, \text{kg} \cdot 5 \, \text{m/s²} = 5000 \, \text{N}$

Therefore, the net force acting on the car is 5000 Newtons.

Example 2:

An airplane with a mass of 5000 kg is flying at a constant velocity of 200 m/s. What is the net force acting on the airplane?

Solution:

Since the airplane is flying at a constant velocity, the net force acting on it is zero. This is because, according to Newton’s second law, when an object is not accelerating, the net force on it is zero.

Factors Affecting the Calculation of Net Force

A. The Impact of Acceleration

Acceleration plays a crucial role in determining net force. As we discussed earlier, a greater acceleration requires a larger net force. The change in velocity, or acceleration, can be caused by external forces such as pushing, pulling, or gravity.

B. The Role of Friction

Friction is another factor that affects the calculation of net force. It is a force that opposes the motion of an object when it is in contact with a surface. Friction can either increase or decrease the net force acting on an object, depending on its direction and magnitude.

C. The Effect of Distance and Time

The distance traveled by an object and the time taken to cover that distance can also impact the calculation of net force. For example, if an object covers a larger distance in a shorter time, it may experience a greater net force due to a higher rate of change in velocity.

Practical Applications of Calculating Net Force

A. Applications in Physics

Calculating net force is essential in various fields of physics. For example, it helps us understand the motion of objects, the behavior of fluids, and the dynamics of particles. It is also used to analyze the forces acting on structures, such as bridges and buildings, to ensure their stability and safety.

B. Applications in Engineering

In engineering, calculating net force is crucial for designing machines, vehicles, and structures. Engineers need to determine the forces involved to ensure the integrity and efficiency of their designs. For instance, in automotive engineering, net force calculations are used to optimize engine performance and fuel efficiency.

C. Real-life Examples

net force calculations are not limited to textbooks and laboratories; they have real-life applications as well. For instance, when you push a car, the net force you apply determines its acceleration. Similarly, when a rocket is launched into space, the net force generated by the engines propels it forward.

How can you calculate net force using mass and velocity, and what are some examples of calculating net force?

To calculate the net force of an object, you can use the formula: net force = mass x velocity. This formula takes into account the mass of the object and its velocity or speed. By multiplying these two values together, you can determine the net force acting on the object. For example, if an object has a mass of 10 kilograms and a velocity of 5 meters per second, the net force can be calculated as 50 Newtons. This Calculating net force with examples. article provides more in-depth information and practical examples of how to calculate net force using mass and velocity.

Common Mistakes and Misconceptions in Calculating Net Force

A. Misunderstanding the Concept of Net Force

One common mistake is confusing net force with individual forces acting on an object. net force is the sum of all the forces acting on an object, while individual forces may cancel each other out or work in the same direction.

B. Errors in Calculating Mass and Velocity

Another mistake is inaccurately determining the mass or velocity of an object. It is vital to use the correct values to obtain accurate results.

C. Overlooking the Impact of Other Factors

Sometimes, people may overlook the impact of other factors such as friction, distance, and time. These factors can significantly affect the net force acting on an object and should be considered in calculations.

And that brings us to the end of our exploration of how to find net force with mass and velocity. We have learned about the relationship between force, mass, and velocity, the formula to calculate net force, factors affecting net force calculation, practical applications, and common mistakes to avoid. Understanding net force is essential for comprehending the motion of objects and designing structures and machines. So, keep these concepts in mind, and happy calculating!

Also Read:

How to Calculate Tangential Velocity

The Formula to Calculate Tangential Velocity

Calculating Tangential Velocity from Angular Velocity

Calculating Tangential Velocity without Time

Calculating Tangential Velocity without Radius

Practical Applications of Tangential Velocity

Finding Tangential Velocity of Planets and Stars

Finding Tangential Velocity of a Point or Particle

Tangential Velocity in Physics and its Relevance

Worked Out Examples

Example of Calculating Tangential Velocity with Centripetal Acceleration

Example of Calculating Tangential Velocity Given Angular Acceleration

Example of Calculating Tangential Velocity from RPM

How do I find the tangential velocity of a projectile and its intersection with the concept of finding horizontal velocity of a projectile?

Numerical Problems on how to find tangential velocity

Problem 1:

Solution:

Problem 2:

Solution:

Problem 3:

Solution:

Constant Negative Velocity Graph

Negative Uniform Velocity Graph

Negative Relative Velocity Graph

Negative Velocity Positive Acceleration Graph

Instantaneous Velocity Negative Graph

Negative Velocity v/s Time Graph Displacement

Negative Slope Velocity Time Graph

Negative Displacement Velocity Time Graph

How to Calculate Distance from Negative Velocity Time Graph?

Frequently Asked Questions

How will you plot a graph from an object accelerating at a speed of 2m/s with its initial velocity of 4m/s?

How to find acceleration from a velocity–time graph?

How to Calculate Velocity with Given Acceleration

Calculating Velocity with Acceleration and Time

Finding Velocity with Acceleration and Initial Velocity

Determining Velocity when Acceleration is Zero

Calculating Velocity when Acceleration is Not Constant

Advanced Concepts in Finding Velocity with Acceleration

Finding Velocity with Acceleration and Displacement

Calculating Velocity with Acceleration and Distance

Determining Velocity with Acceleration and Position

Calculating Velocity with Acceleration and Height

Finding Velocity with Acceleration and Radius

Worked Out Examples

Example of Calculating Velocity with Given Acceleration and Time

Example of Finding Velocity with Given Acceleration and Initial Velocity

Example of Determining Velocity when Acceleration is Zero

Example of Calculating Velocity when Acceleration is Not Constant

Example of Finding Velocity with Given Acceleration and Displacement

How can the concepts of finding velocity with acceleration and mass be combined?

Numerical Problems on How to Find Velocity with Acceleration

Problem 1:

Problem 2:

Problem 3:

The Mathematical Relationship between Velocity, Acceleration, and Initial Velocity

A. The Formula and its Explanation

B. Importance of the Relationship in Physics

How to Calculate Velocity with Acceleration and Initial Velocity

A. Step-by-Step Guide

B. Worked out Examples

Special Cases in Finding Velocity with Acceleration and Initial Velocity

A. When Acceleration is Zero

B. When Initial Velocity is Zero

C. When Both Acceleration and Initial Velocity are Zero

Applications of Velocity, Acceleration, and Initial Velocity Calculations

A. In Everyday Life

B. In Scientific Research

C. In Technological Innovations

How can velocity be determined using both acceleration and height?

Common Mistakes to Avoid when Calculating Velocity with Acceleration and Initial Velocity

A. Incorrect Units

B. Misinterpretation of Negative Values

C. Ignoring the Direction of Motion

How to Find Velocity with Acceleration and Time

Understanding the Basic Concepts

The Relationship between Velocity, Acceleration, and Time

Calculating Velocity with Given Acceleration and Time

How can you find the final velocity without using acceleration, and what is its significance?

Special Cases in Velocity Calculation