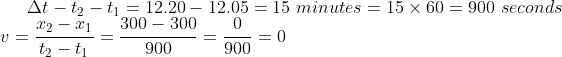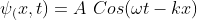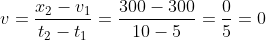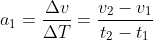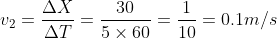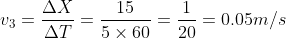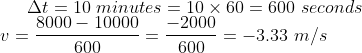Velocity

In this article, we will talk about the zero average velocity along with some examples, and solve some problems.

When the object is at a rest or after displacement tends to return back to the same initial position, then the average velocity of the object is zero.

What is Average Velocity?

The velocity of the object can be determined if there is a displacement of the object in a given time.

The sum of all the velocities of the object varied with time divided by the total number of velocities into consideration gives the average velocity of the object along with time.

Problem 1: A car travels from point A to point B which is 20 km apart. A car traveled first 3 km at a speed of 40km/s, next 7 km at a speed of 70km/h, further at 60km/h to a distance of 6 km, and the remaining 4 km at a speed of 40km/h. Calculate the average velocity of a car.

Given: V₁=40km/h, V₂=70km/h, V₃=60km/h, V₄=40km/h;

Therefore, the average velocity of the car is

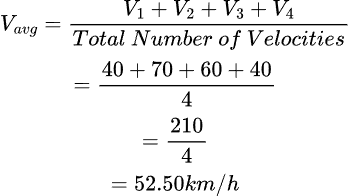
The average velocity of the car to cover a distance of 20kms was 52.50 km/h.

When does the Average Velocity Becomes Zero?

The average velocity will become zero if the sum of all the velocity of the velocities of an object is zero.

This is true if the object is stable at rest position and there is no displacement of the object along with time, or else the object is moving front and back with positive and negative velocity, then the average velocity might become zero.

The object accelerates in the reverse direction accompanied by the negative velocity as the displacement is away from the direction of its motion.

An object on decelerating tends to come at a zero velocity and then accelerates back in the opposite direction with positive acceleration.

Let us understand how we can have zero average velocity with positive and negative velocities by solving below the problems.

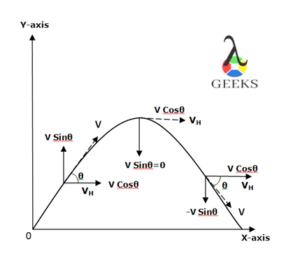
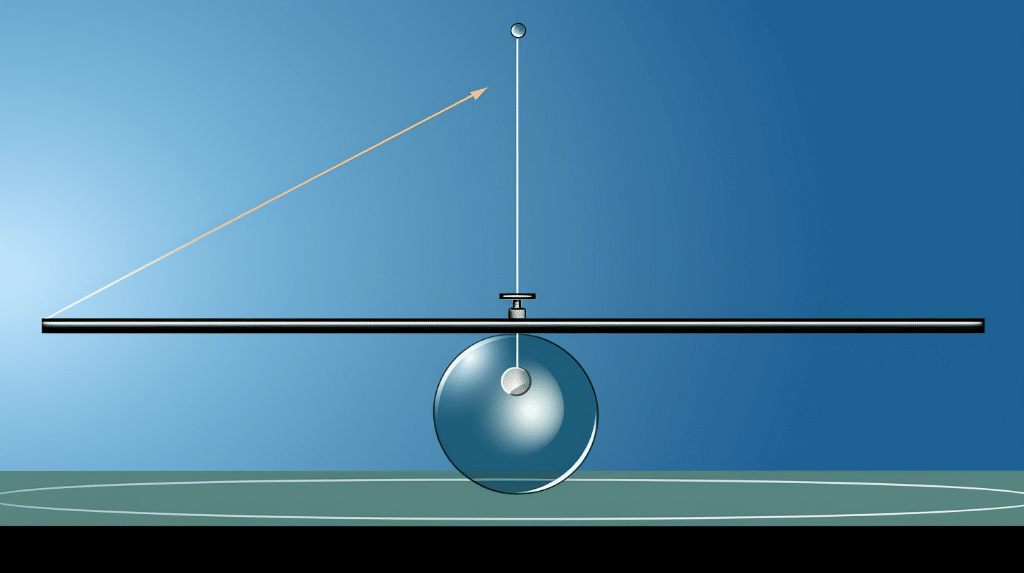
Problem 2: Consider a bob sliding on a semi-arc slide of length 60 cms, every time when it reaches the edges of a slide its velocity becomes zero, and while sliding down from point A it covers 30cms in 2 sec and while sliding upward from the middle, it covers remaining 30 cms in 3 sec to reach point B. Then what will be the average velocity of a bob to reach back to point A?

Solution: Upon releasing from point A, a bob covers a distance of 30 cms in 2 sec, hence the velocity of the bob is

x₁=30cms=0.3m

t₁=2 sec

V₁=x₁/t₁=0.30m/2=0.15m/s

The velocity of bob while climbing up the distance of 30 cm in 3 sec is

V₂=x₂/t₂=0.30m/3=0.10m/s

At the edge, the velocity of the bob becomes zero, because the kinetic energy of the bob is converted into a potential energy that tends the bob to held for a while before its potential energy is converted into kinetic energy due to gravity which force its motion downward and hence exerts a free fall of a bob.

V₃=0

On reversing the motion, the displacement is in the reverse direction and hence the displacement is negative.

Hence, the average velocity of the bob is zero.

Read more on Zero-Velocity Surface.

Why is Average Velocity Zero?

The average velocity is simply the distance covered by the object in a given time.

If the object is found to be in the same position after a certain time, irrespective of the work done or the displacement of the object to come back to the original place, then the average velocity of the object will be zero.

This is seen in the circular motion of the object when the object travels in the circular path and reaches the initial point from where the object had started its journey, and also when the object reverses its direction of motion after certain displacement.

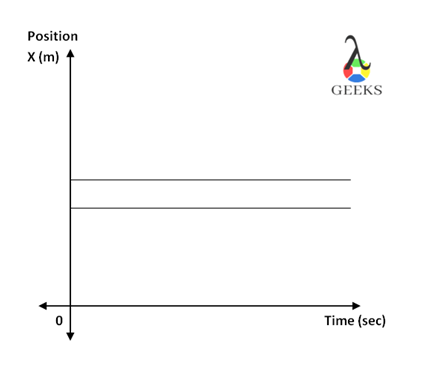
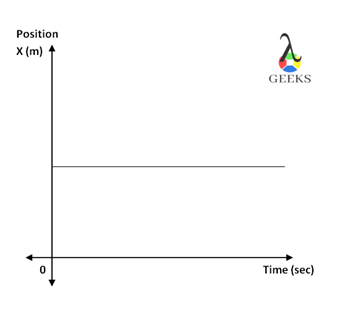
Zero Average Velocity Graph

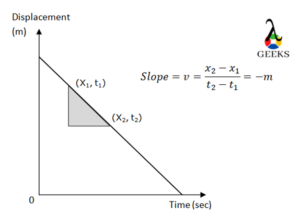
Look at the following position-time graph for the average velocity to be zero.

The above graph shows the position of the object between the time intervals T₁ to T₃. The initial position of the object at time T₁ was x₁ and then displaces to x₂ after time T₂. Since the displacement of the object is to the higher position from that point, the velocity of the object is positive.

The final displacement of the object brings it back to its initial position, which is x₁. As the displacement of the object is to the lower position from its higher position, therefore, the change in displacement of the object is negative and hence the velocity of the object is negative.

The displacement of the object is equal at both the time, and if there is an equal time interval then the velocity of the object is equal and opposite. Therefore, the average velocity of the object will be zero.

Average Velocity Zero Examples

The object at rest, immobile objects, an object moving in a circular path, an object in motion but returning back to the same position, an object accelerating at a point, are some examples of zero average velocity.

If an object accelerates in a particular direction then reverses its direction and moves at the same velocity to reach its initial position then the displacement is zero and the average velocity of the object is zero.

Read more on Zero Velocity: What, How, When, Examples And Problems.

Frequently Asked Questions

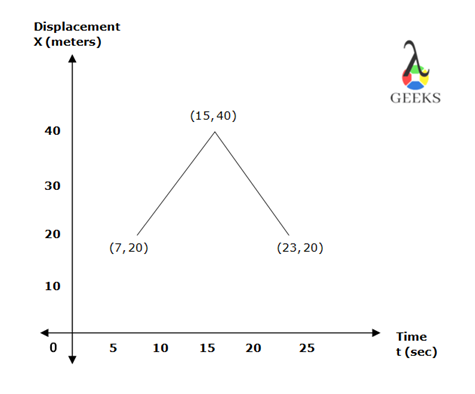
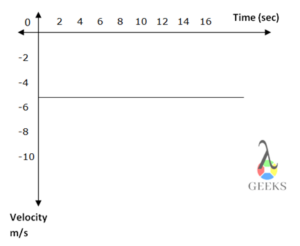
Q1. The object is initially standing at the position 20m away from the origin which travels 20m further for a few seconds and returns back to its initial position. The same is shown in the below graph. Find the average velocity of the object with reference to the graph.

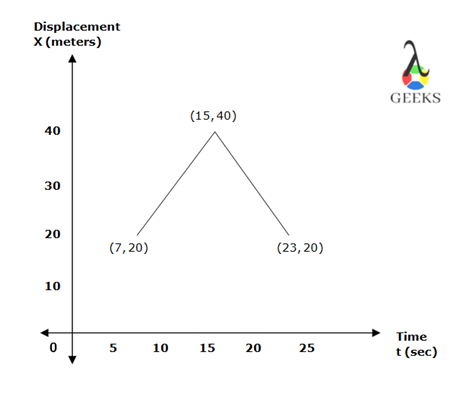
Solution:

The velocity of the object between the time interval t₁=7 sec and t₂=15 sec, the position of the object was x₁=20m and x₂=40m.

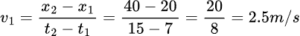
The initial velocity of the object was 2.5 m/s.

The velocity of the object between the time intervals t₂=15 sec and t₃=23 sec, the position of the object was x₂=40m and x₃=20m.

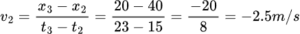
The final velocity of the object was -2.5m/s.

Therefore, the average velocity of the object is

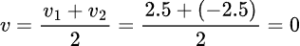
The average velocity of the object is zero.

If we measure the velocity of the direction, that from the first and third position of the object, at time t₁=7 sec and t₃=23 sec, the position of the object was x₁=20m and x₃=20m,

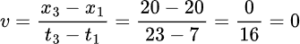
The velocity of the object is still zero.

Q2. A man is walking in a circular path with a diameter of 42m. There are two poles on the two opposite sides to each other. Pole A is straight opposite to pole B at a length of 42m. If a man reaches pole B from pole A in 33 seconds then calculate the velocity of a man. Also, calculate the average velocity of a man on reaching back to pole A and again back to pole B.

Given: The diameter of the circular path is 42m.

Therefore, the radius of the circular path is 21m.

The length of the circular path is equal to the circumference of the circle.

c=2πr=2*(22/7)*21=132m

A man reaches pole B from pole A in 33 seconds, which means man covers half of the circular path in 33 seconds.

Distance covered= 132/2=66m.

A man covers 66m in 33 seconds, hence the velocity of a man is

V₁=(66-0)/33=2m/s

The velocity of a man to reach back to the pole A

V₂=(0-66)/33=-2m/s

Hence average velocity of a man on reaching pole A will be

V=(V₁+V₂)/2=(2-2)/2=0

On reaching again to pole B, the average velocity of a man now is

v=(V₁+V₂+V₃)/3=(2-2+2)/3=2/3=0.67m/s

The average velocity of a man will keep on decreasing on increasing the number of rounds and will become nearly equal to zero.

What is the difference between the zero velocity and the zero relative velocity?

Both imply the zero velocity of the object and the object is fixed in the frame of reference.

When we say that the object has zero velocity, there is no displacement of the object along time and when we talk about the relative velocity, we are looking at the relative displacement of the object in the two different reference frames.

Does the average speed of the object affect if the average velocity of the object is zero?

The average velocity is the change in displacement of the object in a time, whereas the speed is the distance traveled by the object in a time.

If the object returns back to the same position after displacement then the average velocity of the object will become zero, whereas the average speed of the object will be non-zero, because it only measures a distance covered by the object in the duration of time.

Also Read:

• What is constant negative velocity
• Is horizontal velocity constant
• How to calculate velocity in loop quantum gravity
• Velocity vs acceleration
• Centripetal acceleration and velocity
• Velocity unit
• How to find velocity without time
• How to find mass using kinetic energy and velocity
• Horizontal speed vs horizontal velocity
• Instantaneous velocity vs velocity

In this article, we will discuss what zero velocity is, how and when does it come into the scenario with some examples.

An object standing fixed at a point, or on a rigid body and does not displace with time then the velocity of an object is zero.

What is Zero Velocity?

The velocity of the object is defined as a change in its position along with time.

When there is no displacement of the object, the velocity of the object is said to be zero velocity.

The following graph shows the relation between displacement v/s time for zero velocity.

The above graph shows a straight line parallel to the x-axis, which says that the position of the object is the same for all the times; the position of the object does not change. This implies that the object is at rest, which means that the velocity of the object is nil.

When is Velocity Zero?

The object has zero velocity when it does not displace with time.

The velocity of the object is zero when there is no displacement of the object. The position of the object between two different time intervals remains the same.

The velocity is given by the relation v=(Δx/Δt)=(x₂-x₁)/(t₂-t₁)

For velocity to be zero =x₂-x₁; which is understood that the position of the object remains the same. Hence,

v=(x₂-x₁)/(t₂-t₁)=0

Problem: A block of mass ‘m’ was displaced at a distance of 300m and reaches point A at 12.05 pm. It was found that at 12.20 pm the block was present on the same position, that is 300 meters away from the original position. Find the velocity of the block.

Given: x₁=300, x₂=300, t₁=12.05, t₂=12.20

Hence, the velocity of the block is zero.

Zero Velocity Example

Objects at rest, have zero velocity. For example, a ball accelerating comes to a rest, a car climbs up the hill and a driver parks the car there, a coconut fell on the ground, a bird sitting on the branches of a tree, a rock standing on the edge of the mountain, etc.

The objects which are not movable are also examples of zero velocity. Examples are trees, mountains, tables, buildings, chairs, freezers, etc.

What is Zero Group Velocity?

A group, suggests the combination of two or more velocities. The velocity of the object is considered as a form of a wave when it is traveling, hence called a wave velocity.

Two or more waves traveling in a group modulates into a single wave. When the group velocity is zero, the waves diminish into a phase velocity that travels as a single wave, also when it travels through a node or vanishes.

Consider a wave propagating in the x-direction, and then the wave function associated with the wave is

Where A is a amplitude of a wave

ω is a angular frequency which is given by the relation ω=2πt=2πf

k is a wave number, given by k=2πλ

λ is a wavelength

f is a frequency

When a single wave is propagating from a medium, then the velocity of that wave is called a phase velocity and is defined as the ratio of the angular frequency of the wave and the wave number, given by the equation

V_phase=ω/k

This is equal to the number of vibrations seen at two different points in the path length of the wave.

When two or more waves overlap and are modulated into a single wave pattern having the same velocity then the resultant velocity on a combination of all the waves forming a group is called group velocity.

Hence it is derivative of all the phase velocities of individual waves, given by the relation

V_group=dω/dk

When is Group Velocity Zero?

The group velocity is zero at the nodes of a modulated frequency, and when it overlaps with another wave.

When two waves of the same frequencies interfere with each other from the opposite direction, then the group velocity becomes zero.

The single wavelength of the same frequency and amplitude interfere with the group wave and propagates in the direction opposite to the group wave having the same phase velocity, then the group velocity of the waves vanishes and then merges into a single carrier wave.

Read more on Group Velocity.

Zero Instantaneous Velocity

The instantaneous velocity is stated as the displacement of the object that occurred in a very small time interval along its path.

The instantaneous center velocity is zero for the mass at the center of the object which is traveling along with the object moving at a certain velocity.

The instantaneous velocity is given by the formula

• Where Δt is a small interval of time
• V_i is Instantaneous Velocity
• x is a displacement
• t is a time

If an object accelerating in the x-direction, suddenly falls vertical down in negative y-direction, then the displacement of the object will be zero and hence the instantaneous velocity will be zero.

When is Instantaneous Velocity Zero?

The instantaneous velocity will be zero if there is a quick motion without acceleration in a short span.

If the body is in a motion but a part of it is connected rigidly to a certain point on another object, then the instantaneous velocity of that object is zero at that point.

Some examples of zero instantaneous velocity are an object rotating, skipping the rope with two ends of the rope fixed in hand, a woman doing a hula-hoop where the hula-hoop is in motion while the position of a woman is constant hence the velocity of a woman is nil, a point made by the tire of the vehicle attached to the road, the instantaneous velocity at that point is zero, ladder with clamp, compass and divider, and there are various other examples.

Zero Horizontal Velocity

When the object is in a projectile motion, we come across both horizontal and vertical velocity of the object. When the object does not move parallel to the ground then we have zero horizontal velocity.

The projectile motion of the object is shown in the below graph

The y-axis represents the vertical motion of the object and the x-axis represents the horizontal displacement. The vertical velocity is given by the Sin function whereas the horizontal velocity is given by the Cosine function. When the object attains the highest position in its flight, at this point it has converted all its kinetic energy into potential energy and moves parallel to the surface and the vertical velocity of the object is nil. The object is for a longer duration in the air at this point.

When is Horizontal Velocity Zero?

If there is no horizontal displacement of an object the horizontal velocity will be equal to zero.

For a horizontal velocity to be zero, the object must not be in a projectile motion which is a two-dimensional motion, the object must be directed in a y-axis direction.

Lets us demonstrate zero horizontal velocity with a 2-D plot.

Consider a flight of the object of mass ‘m’ in the vertical direction from a fixed point on the horizontal surface. Consider the x-axis as a horizontal surface and the y-axis perpendicular to the x-axis.

This position of the object in the horizontal axis remains fixed before and after the flight of the object. The object moves in a vertically upward direction due to kinetic energy, converts all the kinetic energy into potential energy, and returns back to the ground vertically downward without accelerating in a direction parallel to the surface.

Since there is no change in the position of the object even after the flight; the horizontal velocity of the object is zero. On contrary, there is a vertical displacement of the object which increases and decreases with time. Hence, the object is associated with both positive as well as negative velocity and acceleration.

Zero Velocity and Positive Acceleration

The velocity of the object is zero if there is no displacement, and we will have positive acceleration when there is a change in speed and the direction of motion of the object.

Hence, if the direction of the motion of the object changes frequently then the resultant velocity will be zero and the acceleration will be present.

The object decelerating will come to a rest where its velocity becomes zero and then move with the positive acceleration reversing its direction of the previous motion. Henceforth, we can have positive acceleration with zero velocity of the object.

Zero Uniform Velocity Motion

The object is said to have zero uniform velocity when there is no change in its motion with respect to time and it has no direction.

It is similar to the relative velocity where the velocity of the object appears to be constant for an observer moving at the same velocity and direction.

This is when the object is fixed to the rigid body and it does not displace with time and continue to be in the state of rest. The velocity of such an object is zero.

Consider a rectangular slab moving on a horizontal smooth surface. A donut shape articulate is attached on a rectangular slab which is moving along with the slab.

As the rectangular slab is displacing from one position to another, the position of the articulate remains fixed on the slab. Hence, the velocity of the articulate is zero.

Zero Relative Velocity

If the two objects are traveling at the same velocity and in the same direction then the relative velocity of each with respect to each other will be zero. This is represented as the zero relative velocity.

If two or more objects are traveling in the same direction then their speed cancels out and if the objects are moving in the opposite direction to each other, then their relative will be the sum of the speed of both the objects.

Let the velocities of two different objects be VA and VB. If these objects are moving in the same direction then their relative velocity is V= VA – VB; and if these objects are moving in the opposite direction, then their relative velocity will become V= VA – (-VB)= VA + VB.

Following is a position-time graph for two objects moving will equal speed and direction with time.

Since, both the objects are moving in the same direction their relative velocity is the vector difference of the velocities of both the objects. As both the objects are moving with the same velocities, the relative velocity of the object with respect to each other will be zero.

Consider two cars, Car A and Car B moving in the same lane driving at the same speed. A driver from car A can see a car B moving along with his car and the velocity of car B with respect to Car A is zero. The same is the case when a driver from Car B looks from his point of reference. Hence, the relative velocity of both cars with respect to each other is zero.

Problem: Consider two friends walking in the park with a velocity of 1.5 m/s. A man who is running at a speed of 2m/s in the park in a circle crosses the girls at a certain point. What is the relative velocity of a girl with respect to each other and that of a man?

Given: Velocity of both the girls V_G=1.5m/s

The velocity of a man V_M=2m/s

The direction of motion of both the girls in the same direction and velocity is equal.

V= V_G-V_G=1.5m/s – 1.5m/s=0

Hence, the relative velocity of girls with respect to each other is zero.

A man is also moving in the same direction but with unequal velocity. Therefore relative velocity of a man with that of girls is

V= V_G-V_M=1.5 m/s – 2 m/s= -0.5 m/s.

Hence, the relative velocity of girls with respect to a man is -0.5m/s which is negative. On the contrary, the relative velocity of a man with respect to girls is 0.5 m/s.

Read more on Negative Velocity And Zero Acceleration: How, When, Example And Problems.

Frequently Asked Questions

Q1. Find the instantaneous velocity of the object in a planar motion if the displacement of the object is given by the relation 2t³+2t+3 at time t= 5 seconds.

Given: The position of the object x=2t³+2t+3

The instantaneous velocity of the object is given by

The instantaneous velocity of the object is 152 m/s.

Q2. An object travels a distance of 6 meters in 2 seconds and then reverses its direction and moves again 6 meters in 2 seconds. Then calculate the displacement and the velocity of the object.

The object across 6 m in 2s, then the initial velocity of the object is

v₁=x/t=6/2=3m/s

Then the object reverses its direction and travels the same distance in equal interval of time, hence the final velocity is

v₂=x/t=-6/2=-3m/s

here displacement is negative because the direction of the motion of an object is in the opposite direction.

Hence, the resultant velocity is

V=v₂+v₁=-3+3=0

Since the resultant velocity of the object is zero, the displacement of the object is nil.

Q3. A ball is thrown in the air goes high vertically at a distance of 10 meters and returns down in the same plane after 10 seconds. Measure the vertical and horizontal velocity of the ball.

The time taken for a flight is 10 seconds and the distance covered by the ball in 10 seconds is 20 meters. Hence the velocity of the ball is

v=x/t=20/10=2m/s

Since there is no motion of an object in the horizontal direction; the horizontal velocity of the object is zero.

V_H=0

An object round in shape is moving on a semi arc surface which is 40 cms long in 2 seconds. At what point the instantaneous velocity of the object will be seen?

The instantaneous velocity will be observed throughout the path of the motion.

Well, the velocity of the object will be maximum while accelerating down to a midpoint on the semi-arc surface.

Is trampoline an example of zero horizontal velocity?

A trampoline can be an example of zero horizontal velocity.

The motion of the body is in the vertical direction. The body is thrown upward and then returns down in the same vertical plane and there is no horizontal velocity and the direction attained by the body.

Also Read:

• How to determine velocity in molecular orbitals
• How to determine velocity in quantum decoherence
• How to determine velocity in cosmic inflation
• How to compute velocity in superstring theory
• What is the horizontal velocity of a projectile
• Negative velocity and zero acceleration
• Velocity of sound in air 2
• Centripetal acceleration and velocity
• How to find velocity of an object
• How to find delta velocity

We are going to discuss what zero velocity is, and how to plot a zero velocity graph and different facts about the same.

An object is said to have zero velocity when the displacement of an object does not change with time and is at rest.

Zero Average Velocity Graph

The sum of all the velocities of the object divided by the total number of velocities is called the average velocity.

If the object is at a rest or occupies same position after certain time interval then the object is said to have a zero average velocity.

The positions of the object at different time intervals were noted and when a displacement v/s time graph was plotted for the same, we get a straight line with very few points above or below the lines. Those few points not being on a straight line indicates that there was some minute motion of the object which was negligible.

The above displacement v/s time graph indicates that the object is at rest, but due to some external influences, there is some slight motion seen by an object. On average, the position of the object is fixed. This proves that the velocity of the object is nil.

Position Time Graph for Zero Relative Velocity

The relative velocity depends upon the direction of the motion of two or more objects and is the difference between the velocities of the objects.

If the two objects are moving in the same direction with velocity VA and VB respectively, then their relative velocity is V= VA – VB; and if these two objects are moving in the opposite direction to each other, then their relative velocity will become V= VA – (-VB)= VA + VB.

If the object is at rest then the velocity of the will be equal to zero. The above graph is a position-time graph for two objects at rest. If both the objects are not moving and are stable at rest then it is evident that their relative velocity in concurrent to each other is zero.

Two objects elapsing equal distance in equal intervals of time, then the velocity of both the objects will be equal, and hence relative velocity which is the vector difference of the velocities of both the objects will be zero. Because, from the frame of reference of one object, the position of the other object which is moving along with itself will be constant, hence, the relative displacement will be zero and hence the relative velocity will be zero.

Problem: Consider a lady walking along with her dog on the street with a velocity of 1m/s each crosses a tree. Then what will be the relative velocity of a lady with respect to her dog and that of a tree?

Given: Velocity of a lady V_A=1m/s

The velocity of a dog V_B=1m/s

A tree is at rest and hence the velocity of a tree is V_C=0

The direction of motion of both, a lady and a dog is in the same direction.

V= V_A-V_B=1m/s – 1m/s=0

As a lady crosses a tree, the tree is moving away from a lady at a speed of 1m/s. Since the tree is at rest, in reality, the relative velocity of a lady with respect to a tree is

V= V_B-V_C=1m/s – 0=1m/s

Hence, the relative velocity of a tree and of a lady with respect to each other is 1m/s.

When is Velocity Zero on a Position Time Graph?

The velocity of the object is zero if the position of the object does not change with time.

If the position of the object marked on the position-time graph is the same forming a straight line on a graph between a time interval, then the velocity of the object during that time interval is zero.

The above is the position-time graph for a zero velocity, the straight line on the graph says that the position of the object is constant at all times and there is no displacement.

Suppose at time t₁=5 min the position of the object was found to be x₁=300m and at time t₁=10 min the position of the object was again found to be x₁=300m only, then the velocity of the object

Since there is no displacement, the velocity of the object is found to be zero.

Read more on Zero-Velocity Surface.

Negative Velocity and Zero Acceleration

If the object is accelerating in the direction opposite from its route or the speed decreases with time then the object is said to have a negative velocity.

If the velocity of the object remains constant and is moving in the reverse direction of motion then the velocity is negative and the acceleration of the object is zero.

The above is the graph of negative velocity and time. Since the object after decelerating moves with a constant velocity then the acceleration of the object becomes zero until there is a change in its velocity.

As the negative velocity of the object remains unchanged, the graph of the negative velocity v/s time shows a straight line.

Zero Velocity Graph

The object is said to have zero velocity when there is no displacement of the object. The object at rest remains stable unless and until some external forces are exerted on the body that forces the object to displace from its original position.

Below is a graph for position and time.

It shows that the position of the time remains unchanged for a long duration of time. Since the change of position of the object at different intervals of time is zero; the velocity of the object is zero.

Read more on Negative Velocity Graph: Different Graphs And Their Explanations.

Frequently Asked Questions

Is the object stable if it is not accelerating?

The object is said to be accelerating if its velocity varies with time.

If there is no acceleration means either the object is stable or is moving with constant velocity. If the object is moving then the object is said to have uniform acceleration which does not change with time.

How negative velocity is different from zero velocity?

The objects with zero velocity are fixed at a point whereas those with negative velocity are in reverse motion.

An object with negative velocity is decelerating and hence is in a motion, whereas the object with zero velocity implies that the object is not in motion and is at rest.

An object in a motion can have zero acceleration?

The velocity of the accelerating object is not constant with time.

If the object is moving with a constant velocity with time then the difference between the initial and the final position of the object will be zero and hence the object will have zero acceleration.

What is the effect of zero velocity?

An object with zero velocity will have zero acceleration.

An object will stand fixed at a rest at one position and will not show any displacement unless exerts some external forces.

• 29 Example Of Law Of Conservation Of Mass: Detailed Explanations
• 7 Hydrophilic Examples: Detailed Facts You Should Know!
• 31+ Nuclear Energy Examples: Detailed Facts
• 13 Longitudinal Wave Example: Detailed Explanations
• How To Reverse Drill Direction: The Science Behind It
• Do A Hammer Drill Spin: Why, How To Fix (The Science Behind!)

Also Read:

• How to find velocity in fission reactions
• How to compute velocity in cosmic ray interactions
• How to find magnetic field from velocity
• Relative velocity after collision
• How to find momentum from velocity
• How to find velocity in pulsars and quasars
• How to measure velocity in redshift observations
• Angular velocity and torque
• How to find velocity using huygens principle
• How to find constant acceleration with velocity and time

In this article, we are going to discuss what causes negative velocity and zero acceleration, how does negative velocity exist, with some examples and problems.

When the system moves in the negative axis of its origin or slows down then the object is moving with negative velocity and if the object decelerates with constant rate then the object is said to have a negative velocity with zero acceleration.

What happens to Acceleration when Velocity is Negative?

If the displacement of the object is lowered than its initial movement, then the velocity of the object is reduced and measured as negative.

An object moving with negative velocity, which says that the preceding distance covered by the object with time is lowered, then the acceleration of the object is also reducing at the same time and is negative.

Let us elucidate the acceleration of the object moving with a negative velocity with an example. Consider an object slowing down its speed after traveling for a certain distance. After every 20 seconds, the velocity of the object was noted. The initial velocity of the object was 5 m/s and after 20 seconds it was noted that the velocity of an object was reduced to 3 m/s.

Then, the acceleration of the object is the difference between the final and initial velocity of the object divided by the time interval between which the change has occurred;

a₁=(v₂-v₁)/ΔT=(3-5)/20=-2/20=0.1m/s²

Hence, we can see that the acceleration of the object slowing down is negative as the difference between the final and initial velocity is negative because the initial velocity of the object in motion is greater than that of the final velocity.

If we have a negative velocity of the object throughout its movement, that is, the direction of its displacement is opposite to its motion, then let us see what will be the effect on the acceleration of the object in this circumstance. It is obvious, that the object having negative velocity will reduce its velocity with time as it is decelerating.

Consider an object falling from the hill to the underlying ground area. Let’s say, the initial velocity of the object was -4m/s which then reduced further to -6m/s in 10 seconds then the acceleration of an object will be

a₁=(v₂-v₁)/ΔT==[-6-(-4)]/10=0.2m/s²

Hence, the acceleration of an object will be negative if the velocity of the object is negative. Here, in this example, the velocity is taken as the negative because the displacement of the object is in a negative direction of its motion as it is falling down from the heights.

Read more on Negative Velocity And Negative Acceleration: Why, How, Graph, Example And Detailed Facts.

What is the Example of Zero Acceleration?

The object is said to have zero acceleration if the velocity of the object remains unvaried with time or is at rest.

All the objects at rest or moving with the same initial velocity of the displacement and maintain the same velocity for as long as it is in a motion irrespective of the external forces acting on it, then it is an example of zero acceleration.

Some examples of zero acceleration are, a photon which is a light particle and moves freely at a constant speed without accelerating, an object in space that does not experience the gravitation force and hence floats in the space, an object in a circular motion with its momentum conserved, a rock standing on a hill, a man walking at a constant speed, buoy floating on water, tree, a pole on street, etc.

Conditions for acceleration to be zero

There are two conditions where acceleration can be zero, they are:

Displacement equal to zero.

x=0

For an object at rest, the velocity of the object is zero and hence the acceleration of an object will also be equal to zero.

The initial and final velocity of the object is the same and remains constant.

V_initial=V_final

Well, if the object is in a motion and preserves the constant velocity for all the time then the change in velocity of an object is zero and hence the acceleration is zero.

Negative Velocity v/s Time Graph for Zero Acceleration

The acceleration is zero if the velocity of the object is constant.

The velocity of the object remains the same and does not vary with time, hence we get a straight line on plotting the graph of velocity versus time graph. If the velocity remains the same, whether it is positive or negative, the acceleration will always be zero.

Can Acceleration be Positive when Velocity is Zero?

The acceleration can be positive or negative based on the variation in the velocity of the object.

As there is no velocity which implies that the object is stable at rest, there will be no acceleration of the object since the rate of change of velocity found at different time intervals will also be equal to zero as there is no motion of an object.

Well, all the objects in motion do define the speed, velocity, and acceleration too. The object in motion having zero acceleration implies that the object does have acceleration which is equal to zero. This suggests that the object has a uniform acceleration which does not change with time.

The acceleration of the object will be positive only when the object is moving with the positive velocity that is the velocity of the object adds up with time. If an object travels in the reverse direction or reduces its speed with time then the object will have negative velocity and hence the acceleration is negative. It is only when the object is at rest, its velocity will be equal to zero and therefore the acceleration does not exist in this case.

Read on varying acceleration on jolts.

Frequently Asked Questions

Q1. Consider a car climbing the steeper slope of a mountain, the displacement of a car after every 5 minutes was noted as 50m, 30m, and 15m. Calculate the velocity of a car varied every 5 minutes and hence find the acceleration of a car.

Solution:The displacement of a car in 5 minutes is 50m.

Then the initial velocity of a car for first 5 minutes duration was,

In next 5 minutes, the displacement was 30 m, hence the velocity was

And the final displacement was 15 m in 5 minutes, therefore the velocity was equal to

Hence, the acceleration of a car was

The acceleration of a car is very small but negative as the velocity of a car decreases at a minute rate.

Why does the object have zero acceleration?

An object moving at a uniform velocity or remaining at rest will have zero acceleration.

If there is no external force acting on the object that may have resulted in the change of the velocity or the direction of its motion then the object will continue to remain in a uniform motion with zero acceleration.

Also Read:

• Relative velocity in same direction
• How to find the kinetic energy and velocity
• How to find net force with mass and velocity
• How to compute velocity in neutron stars
• How can you find acceleration from a velocity time graph
• How to find average velocity
• How to find velocity in orbital motion
• How to measure velocity of fluid in porous medium
• How to calculate velocity in nanophysics
• Relative velocity after collision

When it comes to studying projectile motion, understanding the horizontal velocity of a projectile is crucial. The horizontal velocity refers to the speed at which a projectile moves horizontally, parallel to the ground. In this blog post, we will delve into the topic of how to find the horizontal velocity of a projectile. We will explore the formula to calculate it, the factors that affect it, as well as how to determine the initial and final horizontal velocity of a projectile. So, let’s get started!

How to Calculate Horizontal Velocity of a Projectile

Formula to Calculate Horizontal Velocity

To calculate the horizontal velocity of a projectile, we can use a simple formula. The horizontal velocity (Vx) can be determined using the initial velocity (Vi) and the launch angle (Θ). The formula is as follows:

Where:
– Vx is the horizontal velocity
– Vi is the initial velocity
– Θ is the launch angle

Steps to Calculate Horizontal Velocity

Now that we have the formula, let’s go through the steps to calculate the horizontal velocity of a projectile:

1. Determine the initial velocity (Vi) of the projectile.
2. Find the launch angle (Θ) at which the projectile was launched.
3. Use the formula Vx = Vi * cos(Θ) to calculate the horizontal velocity.

Worked Out Example on How to Calculate Horizontal Velocity

Let’s work through an example to solidify our understanding. Suppose a projectile is launched with an initial velocity of 30 m/s at an angle of 45 degrees. Let’s find the horizontal velocity.

Using the formula Vx = Vi * cos(Θ), we can calculate as follows:

Vx = 30 m/s * cos(45 degrees)
Vx = 30 m/s * 0.707
Vx ≈ 21.21 m/s

So, the horizontal velocity of the projectile is approximately 21.21 m/s.

Factors Affecting the Horizontal Velocity of a Projectile

Now that we know how to calculate the horizontal velocity, let’s explore the factors that affect it.

Initial Launch Speed

The initial launch speed, or the magnitude of the initial velocity, directly affects the horizontal velocity of a projectile. The higher the initial launch speed, the greater the horizontal velocity of the projectile.

Angle of Projection

The launch angle, represented by Θ, also plays a significant role in determining the horizontal velocity. The horizontal velocity is maximum when the launch angle is 45 degrees. As the launch angle deviates from 45 degrees, the horizontal velocity decreases.

Gravity and Air Resistance

Gravity and air resistance have minimal impact on the horizontal velocity of a projectile. Since the force of gravity acts vertically downward and air resistance affects the motion of the projectile in the vertical direction, their influence on the horizontal velocity is negligible.

How to Determine the Initial and Final Horizontal Velocity of a Projectile

Finding the Initial Horizontal Velocity

To determine the initial horizontal velocity of a projectile, we need to decompose the initial velocity (Vi) into its horizontal component (Vx) and vertical component (Vy). The horizontal component represents the initial horizontal velocity. We can calculate it using the formula:

 

Finding the Final Horizontal Velocity

The final horizontal velocity of a projectile remains constant throughout its motion if there is no external force acting in the horizontal direction. Therefore, the final horizontal velocity is equal to the initial horizontal velocity. Hence, the final horizontal velocity is also given by:

Worked Out Examples on Initial and Final Horizontal Velocity

Let’s consider an example to illustrate the determination of both initial and final horizontal velocities. Suppose a projectile is launched at an initial velocity of 20 m/s at an angle of 60 degrees. We can calculate both velocities as follows:

Initial horizontal velocity (Vx) = 20 m/s * cos(60 degrees) ≈ 10 m/s

Final horizontal velocity (Vx) = 20 m/s * cos(60 degrees) ≈ 10 m/s

In this case, both the initial and final horizontal velocities are approximately 10 m/s.

How does the horizontal velocity of a projectile relate to finding tangential velocity in physics?

The horizontal velocity of a projectile is the component of its velocity that is parallel to the ground. In physics, tangential velocity refers to the velocity of an object along its curved path. When considering a projectile’s path, the horizontal velocity affects the tangential velocity in important ways. To understand this relationship, it is helpful to explore the concept of Finding tangential velocity in physics. This article provides valuable insights into calculating tangential velocity and sheds light on how the horizontal velocity of a projectile influences it.

How to Calculate the Vertical Velocity of a Projectile

Understanding the Concept of Vertical Velocity

In projectile motion, the vertical velocity refers to the speed at which a projectile moves vertically, perpendicular to the ground. Unlike the horizontal velocity, the vertical velocity is influenced by gravity. It changes continuously throughout the projectile’s trajectory.

Formula to Calculate Vertical Velocity

The formula to calculate the vertical velocity (Vy) of a projectile is given by:

Where:
– Vy is the vertical velocity
– Vi is the initial velocity
– Θ is the launch angle
– g is the acceleration due to gravity (approximately 9.8 m/s²)
– t is the time elapsed

Worked Out Example on How to Calculate Vertical Velocity

Let’s work through an example to calculate the vertical velocity of a projectile. Suppose a projectile is launched with an initial velocity of 30 m/s at an angle of 60 degrees. Let’s find the vertical velocity after 2 seconds.

Using the formula Vy = Vi * sin(Θ) – gt, we can calculate as follows:

Vy = 30 m/s * sin(60 degrees) – 9.8 m/s² * 2 s
Vy = 30 m/s * 0.866 – 19.6 m/s
Vy ≈ 8.8 m/s

Therefore, after 2 seconds, the vertical velocity of the projectile is approximately 8.8 m/s.

And that concludes our exploration of how to find the horizontal velocity of a projectile. We have covered the formula to calculate it, the factors that affect it, as well as how to determine the initial and final horizontal velocity. Understanding these concepts is vital in comprehending the motion of projectiles and their trajectories. Keep practicing and applying these principles in solving projectile motion problems, and you’ll become a pro in no time!

Also Read:

• How to find translational velocity
• How to determine velocity in nuclear physics
• How to calculate velocity in cosmic microwave background
• How to find velocity of a wave
• Relative velocity in opposite direction
• How to find velocity in biophysics
• Escape velocity of earth
• How to calculate velocity of string
• How to determine velocity in pendulum motion
• How to find velocity in laser physics

Negative velocity is a concept that often confuses students when they first encounter it in physics. However, understanding how to calculate negative velocity is crucial for comprehending the motion of objects in different scenarios. In this blog post, we will explore the meaning of negative velocity, its implications in real-world scenarios, and the methods to calculate negative velocity. So, let’s dive in!

The Meaning of Negative Velocity

What Does Negative Velocity Mean in Physics?

In physics, velocity is a vector quantity that represents the rate of change of an object’s position with respect to time. It consists of two components: magnitude (speed) and direction. When the direction of motion is opposite to the chosen positive direction, the velocity is considered negative. Negative velocity indicates that an object is moving in the opposite direction to the reference point or the chosen positive direction.

The Implication of Negative Velocity in Real-World Scenarios

Negative velocity has various implications in real-world scenarios. Let’s consider an example of a car moving along a straight road. Suppose we choose the forward direction as positive. If the car is initially moving forward with a positive velocity and then begins to slow down and move in the opposite direction, its velocity becomes negative. This change in velocity indicates that the car is decelerating or slowing down.

Calculating Negative Velocity

How to Determine Negative Velocity

To determine whether velocity is positive or negative, you need to compare the direction of motion with the chosen positive direction. If the object is moving in the opposite direction, the velocity is negative. Conversely, if the object is moving in the same direction as the chosen positive direction, the velocity is positive.

How to Calculate Negative Average Velocity

Average velocity can be calculated by dividing the displacement of an object by the time taken. Displacement is the change in an object’s position, and it can be negative to indicate a change in the opposite direction. Let’s say an object moves from position to position in a time interval . The average velocity can be calculated using the formula:

If the displacement, , is negative, it means the object has moved in the opposite direction, indicating a negative average velocity.

How to Find Maximum Negative Velocity

Maximum negative velocity refers to the highest speed an object achieves while moving in the opposite direction to the chosen positive direction. It can be calculated using the formula for average velocity, considering the displacement and time interval. The maximum negative velocity occurs when the object is moving at its highest speed in the opposite direction.

Worked Out Examples on Calculating Negative Velocity

Let’s work through a couple of examples to solidify our understanding of how to calculate negative velocity.

Example 1:
A car moves from position to position in a time interval . Calculate the average velocity of the car.

Solution:
Using the formula for average velocity, we have:

Substituting the given values, we get:

The negative sign indicates that the car is moving in the opposite direction to the chosen positive direction.

Example 2:
An object moves from position to position in a time interval . Find the maximum negative velocity of the object.

Solution:
Again, using the formula for average velocity, we have:

Substituting the given values, we get:

The positive average velocity indicates that the object is moving in the chosen positive direction. Therefore, the maximum negative velocity is 2 m/s, which is the highest speed the object reaches while moving in the opposite direction.

The Relationship Between Negative Velocity and Deceleration

Does Deceleration Have a Negative Sign?

Deceleration refers to the rate at which an object slows down. It can be positive or negative, depending on the direction of acceleration. When an object slows down in the same direction as the chosen positive direction, the acceleration is negative. Conversely, when an object slows down in the opposite direction, the acceleration is positive.

Understanding the Link Between Negative Velocity and Deceleration

Negative velocity and deceleration are closely linked. When an object’s velocity is negative, it indicates that the object is moving in the opposite direction to the positive direction. In this case, if the object is also decelerating, it means that it is slowing down while moving in the opposite direction. The negative velocity and negative acceleration reinforce each other, indicating deceleration in the opposite direction.

What is an example of negative velocity in physics and how can it be calculated?

An example of negative velocity in physics is when an object moves in the opposite direction of a chosen reference point. This means that the object is moving in the opposite direction of the positive direction, resulting in a negative velocity value. For calculating negative velocity, you can use the formula v = (xf – xi) / t, where v is the velocity, xf is the final position, xi is the initial position, and t is the time elapsed. An example illustrating negative velocity in physics can be found at Example of Negative Velocity in Physics.

Numerical Problems on how to calculate negative velocity

Problem 1:

A car is moving in the negative x-direction with an initial velocity of -10 m/s. If it accelerates at a rate of -2 m/s^2 for a time period of 5 seconds, calculate the final velocity of the car.

Solution:

Given:
Initial velocity,
Acceleration,
Time,

We can use the formula for calculating final velocity:

Substituting the given values, we get:

Therefore, the final velocity of the car is -20 m/s.

Problem 2:

A ball is thrown upwards with an initial velocity of -15 m/s. The ball decelerates at a constant rate of -3 m/s^2. Calculate the time it takes for the ball to come to rest.

Solution:

Given:
Initial velocity,
Acceleration,
Final velocity,

We can use the formula for calculating time:

Rearranging the formula to solve for time:

Substituting the given values, we get:

Therefore, it takes 5 seconds for the ball to come to rest.

Problem 3:

A train is initially moving with a velocity of -20 m/s. It accelerates at a rate of 4 m/s^2 for 10 seconds and then decelerates at a rate of -2 m/s^2 for 5 seconds. Calculate the final velocity of the train.

Solution:

Given:
Initial velocity,
Acceleration during the first 10 seconds,
Acceleration during the next 5 seconds,
Time during the first acceleration,
Time during the next deceleration,

We can calculate the final velocity using the formula:

Substituting the given values, we get:

Therefore, the final velocity of the train is 10 m/s.

Also Read:

• How to find velocity vector
• Does velocity affect potential energy
• How to calculate velocity in loop quantum gravity
• How to calculate velocity in solid state physics
• How to find velocity of ultrasonic waves
• Velocity vs acceleration graph
• How to find power with velocity and force
• Zero average velocity
• How to measure velocity in event horizons
• How to find acceleration with velocity and distance graph

In physics, velocity is a fundamental concept that describes the rate at which an object changes its position in a given direction. To find velocity with acceleration and mass, we need to understand the mathematical relationship between these variables. This relationship is crucial for determining the final velocity of an object when subjected to certain forces or accelerations. In this blog post, we will dive into this topic and explore the formulas, examples, and step-by-step calculations necessary to find velocity using acceleration and mass.

The Mathematical Relationship Between Velocity, Acceleration, and Mass

The Formula for Velocity

Before we dive into the relationship between velocity, acceleration, and mass, let’s start with the formula for velocity. Velocity is defined as the rate of change of displacement with respect to time. Mathematically, it can be represented as:

Here, displacement refers to the change in position of an object, and time represents the duration in which the change occurs. This formula helps us quantify how fast an object is moving in a particular direction.

How Acceleration and Mass Affect Velocity

Acceleration is the rate at which an object’s velocity changes over time. It can be caused by various factors, such as the application of force or gravitational pull. The equation for acceleration is:

Mass, on the other hand, refers to the amount of matter present in an object. It determines an object’s resistance to changes in motion. The greater the mass, the more force is required to change its velocity. This concept is known as inertia.

When considering velocity, acceleration, and mass together, we need to understand their relationship. The force acting on an object is directly proportional to its mass and acceleration, according to Newton’s second law of motion. Mathematically, this can be expressed as:

Closely related to force is momentum, which is the product of an object’s mass and velocity. It is represented by the formula:

The Relationship Between Velocity and Acceleration

When an object undergoes constant acceleration, the relationship between velocity, acceleration, and time can be represented using the following equation:

This equation shows that the final velocity of an object depends on its initial velocity, the acceleration it experiences, and the duration of the acceleration.

Step-by-Step Guide on How to Calculate Velocity with Acceleration and Mass

Now that we understand the mathematical relationship between velocity, acceleration, and mass, let’s discuss the step-by-step process of calculating velocity using these variables.

Identifying the Given Variables

To calculate velocity, we need to identify the variables given in the problem. These typically include the initial velocity, acceleration, and time. It’s important to have a clear understanding of the problem statement and gather all the necessary information.

Applying the Formula

Once we have the given variables, we can apply the relevant formula to calculate the final velocity. Depending on the problem, we may use the equation for velocity with constant acceleration or the equation for force using mass and acceleration.

Solving for Velocity

After substituting the known values into the formula, we can solve for the final velocity. It’s important to pay attention to the units of measurement and ensure they are consistent throughout the calculation.

Worked Out Examples

Let’s now apply the concepts we’ve discussed to some worked-out examples to further illustrate how to find velocity with acceleration and mass.

Example 1: Finding Velocity with Given Acceleration and Mass

Suppose a car with a mass of 1000 kg experiences an acceleration of 5 m/s². What is the final velocity of the car after 10 seconds?

To solve this problem, we can use the equation for velocity with constant acceleration:

Since the initial velocity is not given, we can assume it to be zero:

After substituting the values, we find that the final velocity of the car is 50 m/s.

Example 2: Calculating Velocity with Mass, Height, and Acceleration

Consider an object with a mass of 2 kg that is dropped from a height of 10 meters. If the object experiences a constant acceleration due to gravity, what is its final velocity just before hitting the ground?

To solve this problem, we need to consider the relationship between gravitational acceleration and velocity. The acceleration due to gravity is approximately 9.8 m/s². Using the equation for velocity with constant acceleration, we can calculate the final velocity:

As the object is dropped from rest, the initial velocity is zero. The time taken to fall can be determined using the equation for displacement with constant acceleration:

Solving for time, we find:

Simplifying the equation, we get:

Substituting the values into the equation for velocity, we find that the object’s final velocity just before hitting the ground is approximately 13.96 m/s.

Example 3: Determining Velocity with Force, Mass, and Acceleration

Suppose a force of 500 N is applied to an object with a mass of 50 kg, resulting in an acceleration of 10 m/s². What is the final velocity of the object?

To solve this problem, we can use Newton’s second law of motion, which states that force is equal to mass multiplied by acceleration:

Rearranging the equation, we can find the acceleration:

Now, we can use the equation for velocity with constant acceleration to find the final velocity:

Assuming the initial velocity is zero, we can solve for the final velocity:

Since the time is not given in the problem, we cannot determine the final velocity without this information.

These worked-out examples demonstrate how to find velocity using acceleration and mass in different scenarios. By applying the relevant formulas and understanding the relationships between these variables, we can calculate the final velocity of an object.

How can you calculate velocity using acceleration and distance?

To calculate velocity using acceleration and distance, you can use the equation v = sqrt(2 * a * d), where v represents velocity, a represents acceleration, and d represents distance. By plugging in the given values for acceleration and distance, you can find the velocity of an object. To learn more about this topic, you can refer to the article on Lambda Geeks: Calculate velocity using acceleration and distance.

Numerical Problems on how to find velocity with acceleration and mass

Problem 1:

A car of mass kg is moving with an acceleration of m/s. Determine the velocity of the car after seconds.

Solution:

Given:
Mass of the car, kg
Acceleration, m/s
Time, seconds

We know that velocity is given by the equation:

Where:
is the final velocity
is the initial velocity
is the acceleration
is the time

Since the car starts from rest (initial velocity ), the equation becomes:

m/s

Therefore, the velocity of the car after 10 seconds is 50 m/s.

Problem 2:

A rocket of mass kg is launched with an acceleration of m/s. Calculate the velocity of the rocket after seconds.

Solution:

Given:
Mass of the rocket, kg
Acceleration, m/s
Time, seconds

Using the equation:

Where:
is the final velocity
is the initial velocity
is the acceleration
is the time

Since the rocket starts from rest (initial velocity ), the equation becomes:

m/s

Therefore, the velocity of the rocket after 5 seconds is 100 m/s.

Problem 3:

A cyclist of mass kg accelerates from rest to a velocity of m/s in a time of seconds. Calculate the acceleration of the cyclist.

Solution:

Given:
Mass of the cyclist, kg
Velocity, m/s
Time, seconds

Using the equation:

Where:
is the final velocity
is the initial velocity
is the acceleration
is the time

Since the cyclist starts from rest (initial velocity ), the equation becomes:

Simplifying the equation:

m/s

Therefore, the acceleration of the cyclist is 1.25 m/s.

Also Read:

• How to find launch velocity
• Is angular velocity a vector
• How to determine velocity in quantum decoherence
• Is angular velocity constant
• How to measure velocity in quantum cryptography
• How to find velocity in electromagnetic waves
• How to measure velocity in astrophysics
• How to find initial velocity
• Negative velocity graph
• How to calculate velocity in magnetic fields

In this article, we are going to discuss about the dependency of the negative velocity and negative acceleration on each other with some examples and graphs.

If the object shifts in the direction opposite to its mobility then the velocity of the object is negative. The acceleration of the object is found to be negative if the velocity of an object decreases with time.

What is Negative Velocity?

A negative velocity is a ratio of the displacement of an object in a direction away from its direction of motion.

If the direction of motion of an object is opposite then the displacement then the velocity of the object is negative.

The velocity is given by the equation

v=(Δx/Δt)=(x₂-x₁)/(t₂-t₁)—(1)

For velocity to be negative in the above equation (1),

x₂>x₁

The final displacement of the object should be less than the initial displacement.

What is Negative Acceleration?

An object slowing down with time will show the reduction in the velocity of the object with time and distance.

An object is said to be accelerating if there is a change in the velocity of an object during its motion. The velocity of an object varies and lowers along with the displacement, the speeding down of an object will lower the acceleration of an object.

a=(Δv/Δt)=(v₂-v₁)/(t₂-t₁)

For acceleration to be negative in the above equation (2),

v₂>v₁

For acceleration to be negative, the initial acceleration of an object should be greater than the velocity of the object on further accelerating.

Can you have Negative Velocity and Negative Acceleration?

This is possible in the case of an object slowing down its speed, or falling from a greater height, or moving away from the original direction of motion, reversing its direction.

If the position of an object changes away from its direction of motion and velocity decreases with time, then the object has negative velocity and negative acceleration both.

We can consider a simple example of a comet approaching the Sun from afar nebula by attracting towards the gravitational force of the Sun. But as it approaches near the Sun, it gains potential energy and diverts back from its direction of motion, and accelerates away from the Sun in a parabolic path.

As the comet is far from the Sun, its speed is about 2000 miles per hour, once it reaches near the Sun its speed becomes nearly 100000 miles per hour due to the external gravitational pull of the Sun on the comet. On deflecting from the Sun, its speed is even high and decreases as the distance from the Sun increases.

Hence the velocity of the comet is actually negative while traveling away from the Sun and hence the acceleration is also negative as the velocity decreases with time.

Read more on comets.

Negative Velocity Negative Acceleration Graph

To measure the velocity of the object, we have to plot a graph of displacement of an object at different time duration. The following is a position-time graph of a decelerating object.

The graph shows that the displacement of an object is in a reverse direction and the position of an object from its origin decreases with time. On finding the slope of a position-time graph, you will find the velocity of the graph. In the above graph, the velocity of the object decreases with time and hence the velocity is calculated to be negative.

To find out the acceleration of an object, we plot a graph of velocity v/s time rate of change of velocity. The graph is as follows:

From the graph, we can see that the velocity linearly drops with time. The slope of a graph gives the acceleration of an object. Since the velocity reduces with time, the acceleration is negative.

If the object accelerates at a higher velocity than the previous, then we will have a positive slope of a graph and hence a positive acceleration.

Negative velocity and negative acceleration example

Consider an airplane traveling at a speed of 850 km/h accelerates at a lower altitude to a speed of 580 km/h and then speeds down to the surface of the Earth lowering its speed during its landing. The horizontal velocity of the plane is deduced while the vertical velocity also decreases while the plane is landing on the ground.

Here, in this case, the distance between the airplane and the landing area decreases with time. Initially, the airplane was flying at a height of 10,000 meters above the surface and then follows the lower altitude at a height of 8000 meters in 10 minutes. Then the velocity can be calculated as the change in position with respect to the initial position and the time given by the equation

v=(x₂-x₁)/(t₂-t₁)

Here, x₁=10000 meters, x₂=8000 meters,

Hence, the velocity of the plane while coming down to the lower altitudes is -3.33 m/s. It is seen that as the height of the plane decreases its velocity is calculated and found out to be negative.

The acceleration of a plane is a varied velocity with time, given by the relation

a=(v₂-v₁)/Δt

The initial velocity of the airplane was 850km/h which was then reduced to 580km/h. Hence, the acceleration of the plane with decreasing velocity is

We have v₁=850 km/h, v₂=580 km/h, Δt=600 seconds

a=(580-850)/600=-270/600=-0.45m/s²

Since the velocity decreases with time, the acceleration becomes negative.

How Negative Velocity and Negative Acceleration Works?

The velocity is directly related to the change in the displacement whereas the acceleration of the object depends upon the change in its velocity.

The negative velocity reverses the direction of the object as the displacement is in the negative axis of the system while the speed of the object is reduced due to negative acceleration.

The negative velocity pulls back the object in a direction opposite to its motion and the negative acceleration slows down the speed of an accelerating object and hence it decelerates.

The object falling on the ground from a certain height converts the potential energy to the kinetic energy utilized to displace itself from the height to the ground surface. The height of the object from the ground from where its flight was initially started decreases. Compatibility, the velocity of the object is negative as the displacement of an object is in a negative axis.

Suppose we throw an object in a projectile motion, the velocity of the object on reaching the highest height reduces once all the kinetic energy of the object is converted back into the potential energy of the object.

From here the velocity of the object initially increases as the potential energy is converted into kinetic energy and due to the gravitational force acting on the object, and then slightly decreases the velocity while accelerating downward and deducts sharply when it reaches near the surface of the Earth.

As the velocity decreases with time, the difference in the preceding and the initial velocity is negative and hence the acceleration of the object is negative.

When Velocity is Negative and Acceleration is Negative what is happening to the Object?

When the velocity is negative of the object the displacement is in the reverse direction and when acceleration is negative the speed of the object accelerating is reduced.

As the velocity and as well as the acceleration of the object decreases, the kinetic energy of the object is converted into the potential energy of the object. We can even consider that there is some external impact on the object due to which the velocity of the object lowers.

Read more on Negative Velocity Graph: Different Graphs And Their Explanations.

Frequently Asked Questions

Q1. How does the graph of velocity v/s time for the comet approaching the Sun and then deflecting back will look like? Explain the graph for the same regarding velocity and acceleration.

The speed of the comet while approaching the Sun from the far distance is around 2000km/h, and increases as the gravitational pull on the comet increases with decreasing distance

The speed becomes approximately 1L km/h when it is near the Sun. Hence, the change in velocity of the comet is positive and therefore the acceleration of the comet is also positive as shown in the graph below.

It receives the energy from the sun and sweeps back against the gravitational pull of the Sun gradually decreasing its velocity as it elapses the distance away from the Sun. Initially, there will be a major fall in the velocity as the comet will lose its extra energy received from the radiation of the Sun quickly.

Since the velocity of the comet decreases the acceleration of the comet is negative and the same is shown in the graph where the velocity is sloping down with time.

Q2. Consider an object slowing down, base on the displacement of an object away from its original position with time the velocity was calculated and plotted for the same time interval. The graph is shown below. Based on the following graph calculate the acceleration of the object when time is equal to 5 seconds.

Solution: From the above graph, the velocity of the object at time t=5seconds, the velocity of the object was v=-20 m/s.

The velocity is the product of the acceleration of the object during that time.

Hence, the acceleration of the object is

Therefore, the acceleration rate of an object at time t=5 seconds was -4m/s².

Is negative acceleration the same as the deceleration of the object?

The acceleration of the object is negative if the velocity of the object is lowering with time.

If the velocity of the object along with the distance decreases, then the object is said to be decelerated with time. The decelerating object accompanies with negative acceleration.

Why does the velocity of a falling object from the height be negative?

If the object moves in a reverse direction then the difference between the final and initial displacement is negative.

Since the displacement of a falling object is in a reverse direction, its velocity and hence the acceleration will be negative.

Is it possible to measure the distance covered by an object from its velocity-time graph?

Yes, the displacement of an object can be found from the velocity-time graph.

Since velocity is defined as a distance elapsed by the object in a given time, then distance will be equal to the velocity of the object during that time and the time duration at which the velocity was noted.

Also Read:

• How to find torque from angular velocity
• Is angular velocity a vector
• How to determine velocity in plasma physics
• Zero velocity graph
• How to measure velocity in x ray diffraction
• How to find velocity with acceleration and distance
• How to compute velocity in stellar dynamics
• How to derive velocity in thermodynamics
• Find coefficient of friction given velocity and distance
• How to find velocity in quantum chromodynamics

In this article, we are going to discuss some negative velocity examples and solve related problems.

Some examples of negative velocity are as follow:-

Object falling down

An object accelerating down from greater heights to down the surface decreases its position while accelerating. Since the position decreases with time, the velocity of the object is negative.

The energy of the object is always conserved; it only changes from one form of energy to another. While the object accelerates upward its kinetic energy utilized for its drift is converted into potential energy and once all the kinetic energy is converted into the potential energy, the object starts accelerating down to zero potential surfaces.

Since the energy is conserved in the form of the potential and kinetic energy of the object falling from the heights, its initial energy produced will be equal to the final energy.

KE₁+PE₁=KE₂+PE₂

1/2 mu₁²+mgh₁=1/2 mv₂²+mgh₂

1/2 u₁²+gh₁=1/2 v₂²+gh₂

u₁²+2gh₁=v₂²+2gh₂

u₁²-v₂²=2g(h₂-h₁)

v₂²=u₁²-2g(h₂-h₁)

v₂=√u₁²-2g(h₂-h₁)

In short, kinetic energy is equal to the potential energy of the object

1/2 mv²=mgh

v²=2gh

v=√2gh

This implies that the velocity of the object during its flight in the air depends upon the height at which it is above the surface of the ground.

As the height of the falling object decreases, the velocity of the object will decrease by the square root of its height. Hence the velocity of an object is negative in this case.

Slipping of feet while trying to climb up the slider

You must have noticed that due to lack of frictional force on the slider, we repeatedly slide backward while climbing up the slider from the slide. This reduces the velocity of a person while climbing and often sliding back to the ground. Hence, this is also an example of a negative velocity.

Object slowing down

The fast accelerating object suddenly lowers its velocity then we have an exponential decrease in the velocity of the object.

For such objects, the acceleration will also be negative.

An object moving in a reverse direction with high speed

While moving in a reverse direction from the original point then the position of the object with respect to the origin will decrease, hence the velocity of the object which is a change in position with time will be negative.

When the object takes sharp reverse acceleration, then the acceleration is positive but the velocity of the object is negative.

Kingfisher diving in a river for fish

A bird, kingfisher diving into the river water to catch the fish for its food moves with negative velocity as it comes near the surface of the water from the height at which it was flying.

Light traversing through the medium

As light travels from one medium to another, the speed of light changes. On entering the denser medium the speed of light rays decreases, hence is also an example of negative velocity, because the distance elapses by the light in the air in one second is more as compared to its velocity in the denser medium, as it travels slower comparably.

Read more on the speed of light.

Spring

Spring always tries to regain its original size upon stretching. If a heavy mass is attached to one end of the spring comparable to its spring constant and keeping the other end fixed, upon stretching the spring by pulling a mass on a horizontal slide, it will build potential energy which will be converted into kinetic energy once it is released.

The mass will travel in a reverse direction due to equal and opposite reactions and will displace at a position towards the fixed point and remain stable. This is an instantaneous process. Since the position decreases with time the velocity is negative.

Flow of current

The direction of a flow of current is in the direction opposite to the motion of electron charges; this also can be accounted for a negative velocity of electrons compared to the direction of the current.

Solved Problems

Problem 1: A car travels a distance of 7km in 7min and then slows down on reaching the district road and travels 3km in 9minutes. Calculate the change in velocity.

Solution: A car displaces 7 km from the original point, x₁=7km, time taken t₁=7min;

Hence the speed of the car is

v₁=x₁/t₁=7* 60/7=60km/h

A car travels 3 km in 9 minutes, hence the speed of the car is

v₂=x₂/t₂=3*60/9=20km/h

Hence change in velocity is

V=V₂-V₁=20-60=-40km/h

The change in the velocity of the car becomes negatives once it slows down.

Problem 2: A weight of mass 1kg is kept on a horizontal slide made up of glass. A weight is attached to a spring of length 1 meter whose other end is sealed in a wall. A mass is pulled to a distance of 50 cm away from its position on applying a force and relieved. After which the weight displaces 80 cm in a second and rests at a position 80 cm away from the wall.

Find the instantaneous velocity of a mass and the potential energy of spring on pulling the mass. Also, calculate the potential energy stored in the spring when it was displaced at a distance of 50 cm from its resting position. Given the spring constant k=1.5.

Solution:

Given: x₁=50cm, x₂=80cm, t₁=0, t₂=1sec;

Instantaneous\ Velocity=x₂-x₁/t₂-t₁=50-80/1-0=-30cm/s=-0.3m/s

Velocity of a weight is -0.3m/s which are negative because the weight displaces in the reverse direction.

Problem 3: Find the average velocity of an object traveling with time. The distance elapsed by the object at different times was noted, the same is shown in the following table. Plot the graph for the same.

Displacement(km)	Time(min)
10	10
8	20
6	30
4	40

Solution: The position-time graph for the above data is as below

Change in velocity with respect to time is equal to the slope of the graph.

v₁=x₂-x₁/t₂-t₁=8-10/20-10=-2/10=-2*1000/10*60m/s=-3.3m/s

v₂=x₂-x₁/t₂-t₁=6-8/30-20=-2/10=-2*1000/10* 60m/s=-3.3m/s

v₃=x₂-x₁/t₂-t₁=4-6/40-30=-2/10=-2*1000/10*60m/s=-3.3m/s

v₄=x₂-x₁/t₂-t₁=4-8/40-20=-4/20=-4*1000/20*60m/s=-3.3m/s

It is seen that the velocity of the object remains constant but the position of the object decreases with increasing time, hence the velocity of the object is negative.

The potential energy of a spring is half time the spring constant and a square of the displacement.

U=1/2kx²

=1/2*1.5*0.5²

=1/2*1.5*0.25

=0.19 Joules

Hence, the energy stored in the string was 0.19 Joules.

Problem 4: A girl walks 100meters towards North in 1minute and returns back to the point from where she had started and walks 200meters towards South from there in 4minutes. Calculate her actual velocity and displacement to reach that point where now she is.

Solution: A girl walks 100meters initially towards North in 1minute hence her walking speed was

Speed=Distance/Time

v₁=100/60=1.67m/s

Then, a girl covers 200meters in 4minutes, therefore the velocity of a girl is

v₂=200/4*60=0.83m/s

Therefore, the velocity of a girl in 5minutes is

V=V₂-V₁=0.83-1.67=-0.84m/s

And actual displacement of a girl from original position is

x=x₂-x₁=200-100=100meters

That is 100 meters towards the South from the original position.

Problem 5: What is the velocity of an object when it is at a height of 10 meters above the ground and how does the velocity of the object vary at what rate?

Solution: The velocity of the object during its flight in the air is proportional to the square root of its height from the ground and the acceleration due to gravity of the Earth given by the relation

v=√2gh

When the object is at a height of 10 meters, it velocity will be equal to

v=√2*9.8*10=√196=14 m/s

When h=9m

v=√2*9.8*9=√176.4=13.28 m/s

When h=8m

v=√2*9.8*8=√156.8=12.52 m/s

When h=7m

v=√2*9.8*7=√137.2=11.71 m/s

When h=6m

v=√2*9.8*6=√117.6=10.84 m/s

When h=5m

v=√2*9.8*5=√98=9.8 m/s

When h=4m

v=√2*9.8*4=√76=8.7 m/s

When h=3m

v=√2*9.8*3=√58.8=7.67 m/s

When h=2m

v=√2*9.8*2=√39.2=6.26 m/s

When h=1m

v=√2*9.8*1=√19.6=4.43 m/s

Height (m)	Velocity(m/s)	Acceleration
10	14	-0.72
9	13.28	-0.76
8	12.52	-0.81
7	11.71	-0.87
6	10.84	-1.04
5	9.8	-1.10
4	8.7	-1.03
3	7.67	-1.41
2	6.26	-1.83
1	4.43	-4.43

This indicates that, as the height decreases, the velocity of an object decreases, and hence acceleration also decreases. The acceleration of the object sharply decreases when it is near the ground surface.

Problem 6: A ray of light enters a bucket of water and passes through a glass slab placed in it. Find the velocity of the light rays in each medium. The refractive index of water is 1.3 and that of glass is 1.5.

Solution: RI of water is n=1.3,

n=c/v

v=c/n=3⊓*10⁸*1.3

v=2.3*10⁸m/s

Now the velocity of light is 2.3*10⁸m/s. Hence, the speed of light in glass is

n=v₁/v₂

v₂=v₁/n=2.3*10⁸/1.5

v=1.5*10⁸m/s

Hence the velocity of light in glass is *10⁸m/s.

Read more on Negative Velocity Graph: Different Graphs And Their Explanations.

Frequently Asked Questions

Why velocity is negative?

Velocity is defined as a change in the position of an object with different time intervals.

If the position of an object shifts with time, the difference in position with respect to its previous position will be negative and hence velocity will be negative compared to the preceding interval.

How phase velocity of light can be negative?

Distance traveled by a single ray of light or single wave in one second of time is called phase velocity.

Negative velocity comes into a scene while light travels from one medium to another because the speed of light decreases on entering the denser medium.

Also Read:

• How to find acceleration with velocity
• How to find velocity with x and y components
• Relative velocity and speed of light
• How to measure velocity in quantum entanglement
• How to measure velocity of fluid in porous medium
• How to determine velocity in atomic collisions
• How to measure velocity in spectrometry
• How to measure velocity in gas laws
• How to find radial acceleration without velocity
• How to find final velocity with acceleration and distance