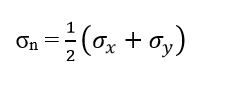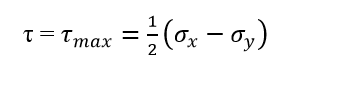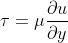Seismology is the scientific study of earthquakes and the energy they release. Seismologists are the professionals who study seismic activity and interpret the data collected from seismometers and other instruments to determine the location, magnitude, and other characteristics of earthquakes. This comprehensive guide will delve into the intricate world of seismology, providing a detailed and technical exploration of the tools, techniques, and principles that seismologists rely on to unravel the mysteries of our dynamic planet.
Measuring Earthquake Severity: Intensity and Magnitude
To quantify the severity of an earthquake, seismologists utilize two primary scales: intensity and magnitude. Intensity is a measure of the shaking experienced at a particular location, and it is typically assessed using the Modified Mercalli Intensity (MMI) scale, which ranges from I (barely perceptible) to XII (total destruction). Magnitude, on the other hand, is a measure of the total energy released by the earthquake, and it is most commonly expressed using the moment magnitude scale (Mw).
The moment magnitude scale (Mw) is based on the seismic moment of the earthquake, which is a function of the size of the rupture area, the average slip, and the rigidity of the rocks involved. The formula for calculating the moment magnitude (Mw) is:
Mw = (2/3) log(M0) – 6.0
Where M0 is the seismic moment, measured in Newton-meters (N·m). This scale is preferred over the older Richter scale (ML) because it provides a more accurate representation of the earthquake’s energy release, particularly for large earthquakes.
Seismometers: The Backbone of Seismology

Seismometers are the primary instruments used by seismologists to measure ground motion. These devices work on the principle of inertia, where a suspended mass tends to remain still when the ground moves. This motion is then converted into electrical signals, which are recorded as seismograms.
To measure the actual motion of the ground in three dimensions, seismometers employ three separate sensors within the same instrument, each measuring motion in a different direction: up/down (Z component), east/west (E component), and north-south (N component). This allows seismologists to obtain a comprehensive understanding of the ground’s movement during an earthquake.
Seismometers can be classified based on several technical specifications, including:
-
Frequency Response: Broadband seismometers used for studying tectonic processes have a flat frequency response from 0.001 to 100 Hz, while strong-motion seismometers used for studying building response to earthquakes have a flat frequency response from 0.1 to 100 Hz.
-
Period: Short-period seismometers have a natural period of less than 1 second and are used for measuring high-frequency seismic waves, while long-period seismometers have a natural period of more than 10 seconds and are used for measuring low-frequency seismic waves.
-
Sensitivity and Dynamic Range: High-sensitivity seismometers are used for measuring small earthquakes and ambient noise, while low-sensitivity seismometers are used for measuring large earthquakes and strong ground motion. Sensitivity is a measure of the minimum detectable ground motion, while dynamic range is a measure of the ratio of the largest to smallest measurable ground motion.
Locating Earthquakes: Seismic Wave Arrival Times
Seismologists use the arrival times of different seismic waves to locate the epicenter of an earthquake. Seismic waves are classified into two main types: body waves and surface waves. Body waves, which include P-waves (primary or compressional waves) and S-waves (secondary or shear waves), travel through the Earth’s interior, while surface waves, such as Rayleigh and Love waves, travel along the Earth’s surface.
P-waves are the fastest seismic waves and are the first to arrive on a seismogram, followed by the slower S-waves, and then the surface waves. By comparing the arrival times of these waves at different seismometers, seismologists can determine the location of the earthquake’s epicenter using the following equations:
t_p = t_0 + (r/v_p)
t_s = t_0 + (r/v_s)
Where:
– t_p and t_s are the arrival times of the P-waves and S-waves, respectively
– t_0 is the origin time of the earthquake
– r is the distance between the earthquake and the seismometer
– v_p and v_s are the velocities of the P-waves and S-waves, respectively
By solving these equations for multiple seismometer locations, seismologists can triangulate the earthquake’s epicenter.
Seismic Wave Propagation and Attenuation
The propagation and attenuation of seismic waves are crucial factors in seismology. Seismic waves travel through the Earth’s interior and are affected by the varying properties of the materials they encounter. The velocity of seismic waves is primarily determined by the density and rigidity of the medium, as described by the following equations:
v_p = sqrt((K + 4/3 * μ) / ρ)
v_s = sqrt(μ / ρ)
Where:
– v_p and v_s are the velocities of the P-waves and S-waves, respectively
– K is the bulk modulus of the medium
– μ is the shear modulus of the medium
– ρ is the density of the medium
As seismic waves propagate, they also experience attenuation, which is the reduction in their amplitude due to various factors, such as geometric spreading, intrinsic absorption, and scattering. The attenuation of seismic waves is often described by the quality factor (Q), which is a measure of the energy dissipation in the medium.
Seismic Imaging and Tomography
Seismologists use advanced techniques, such as seismic imaging and tomography, to create detailed models of the Earth’s interior structure. Seismic imaging involves the use of seismic reflection and refraction data to generate images of subsurface structures, while seismic tomography uses the travel times of seismic waves to construct three-dimensional models of the Earth’s interior.
One of the most widely used seismic imaging techniques is the reflection seismic method, which involves the generation of seismic waves and the recording of the reflected waves at the surface. The time it takes for the waves to travel from the source to the reflector and back to the surface can be used to determine the depth and structure of the subsurface layers.
Seismic tomography, on the other hand, relies on the analysis of the travel times of seismic waves through the Earth’s interior. By measuring the arrival times of seismic waves at various seismometers, seismologists can infer the velocity structure of the Earth’s interior, which can then be used to create three-dimensional models of the Earth’s structure, including the crust, mantle, and core.
Seismic Hazard Assessment and Risk Mitigation
Seismologists play a crucial role in assessing seismic hazards and developing strategies for risk mitigation. By analyzing historical earthquake data, seismologists can identify regions with high seismic activity and estimate the likelihood of future earthquakes. This information is used to create seismic hazard maps, which are essential for urban planning, infrastructure design, and emergency preparedness.
Seismic hazard assessment involves the evaluation of several factors, including the frequency and magnitude of past earthquakes, the tectonic setting of the region, and the local soil conditions. Seismologists use probabilistic seismic hazard analysis (PSHA) to quantify the likelihood of different levels of ground shaking occurring at a given location within a specified time frame.
Risk mitigation strategies developed by seismologists include the implementation of building codes and structural design standards, the development of early warning systems, and the promotion of public awareness and preparedness programs. By working closely with engineers, policymakers, and emergency management agencies, seismologists can help communities become more resilient to the devastating effects of earthquakes.
Emerging Trends and Advancements in Seismology
The field of seismology is constantly evolving, with new technologies and analytical techniques being developed to enhance our understanding of the Earth’s dynamic processes. Some of the emerging trends and advancements in seismology include:
-
Distributed Acoustic Sensing (DAS): This technology uses fiber-optic cables to measure ground motion, providing a dense network of seismic sensors that can be deployed in remote or inaccessible areas.
-
Machine Learning and Artificial Intelligence: Seismologists are increasingly leveraging machine learning algorithms to automate the detection, classification, and analysis of seismic events, leading to more efficient and accurate data processing.
-
Integrated Geophysical Approaches: Seismologists are combining seismic data with other geophysical measurements, such as gravity, magnetism, and electrical resistivity, to create more comprehensive models of the Earth’s structure and composition.
-
High-Performance Computing: The growing availability of powerful computing resources has enabled seismologists to develop more complex and detailed models of the Earth’s interior, as well as to perform large-scale simulations of earthquake processes.
-
Citizen Science and Crowdsourcing: Seismologists are engaging the public in data collection and analysis through citizen science initiatives, leveraging the power of crowdsourcing to enhance their understanding of seismic activity.
As seismology continues to evolve, seismologists will play an increasingly vital role in advancing our knowledge of the Earth’s structure and dynamics, as well as in developing strategies for mitigating the risks posed by earthquakes and other natural hazards.
References:
- Seismology, Geology & Tectonophysics Division | Lamont-Doherty Earth Observatory. Retrieved from https://lamont.columbia.edu/research-divisions/seismology-geology-tectonophysics
- Seismological Data Acquisition and Analysis within the Scope of … (n.d.). Retrieved from https://www.intechopen.com/chapters/74466
- Which Picker Fits My Data? A Quantitative Evaluation of Deep … (2022). Retrieved from https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2021JB023499
- How are earthquakes detected? – British Geological Survey. Retrieved from https://www.bgs.ac.uk/discovering-geology/earth-hazards/earthquakes/how-are-earthquakes-detected/
- Thorne Lay (PhD ’83), Seismologist – Caltech Heritage Project. Retrieved from https://heritageproject.caltech.edu/interviews-updates/thorne-lay




![Rendered by QuickLaTeX.com \\Rightarrow W=\\frac{K}{-\\gamma +1}\\left [ \\frac{V_{2}}{V_{2}^{\\gamma }}-\\frac{V_{1}}{V_{1}^{\\gamma }} \\right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-822c0240c5b649e8f8cefdb4e568a85d_l3.png)
![Rendered by QuickLaTeX.com \\Rightarrow W=\\frac{1}{-\\gamma +1}\\left [ \\left ( \\frac{K}{V_{1}^{\\gamma }} \\right )V_{1}-\\left ( \\frac{K}{V_{2}^{\\gamma }} \\right )V_{2} \\right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-0b7fc1d22de4b022f0080ad99aaccd79_l3.png)
![Rendered by QuickLaTeX.com \\Rightarrow W=\\left ( \\frac{1}{\\gamma -1} \\right )\\left [ P_{1}V_{1}-P_{2}V_{2} \\right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-84c8264f47e0cd24206031aa8134e8c8_l3.png)
![Rendered by QuickLaTeX.com \\Rightarrow W=\\left ( \\frac{1}{\\gamma -1} \\right )\\left [ nRT_{2}-nRT_{1} \\right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-01bed27383ecd0585e78c5a10c4fb11d_l3.png)
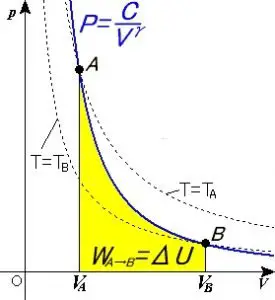
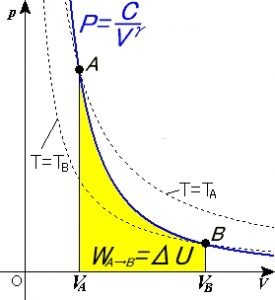
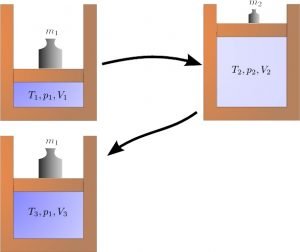
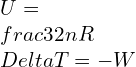
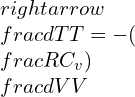
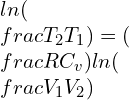
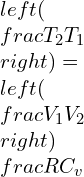
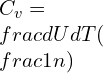
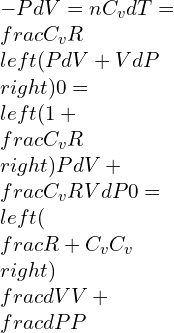

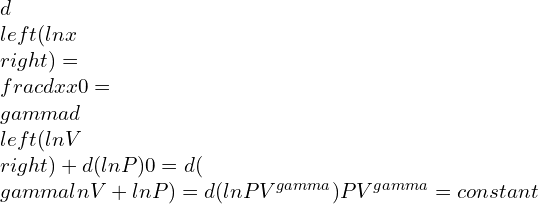
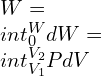 —–(1)
—–(1)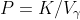
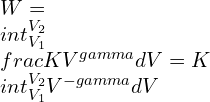
![Rendered by QuickLaTeX.com W=kleft | frac{V^{1-gamma }}{1-gamma } right |=frac{K}{1-gamma }left [ V_{2}^{1-gamma }-V_{1}^{1-gamma } right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-4b36353a4188600233e8d19d1e3e334c_l3.png)
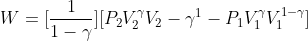
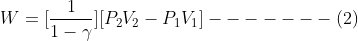
![Rendered by QuickLaTeX.com W=left [ frac{R}{1-gamma } right ]left [ T_{2}-T_{1} right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-8679105960c7b3c775fdb83e49bec52d_l3.png)
![Rendered by QuickLaTeX.com W=left [ frac{R}{gamma-1 } right ]left [ T_{1}-T_{2} right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-4fcbba1eadf9f6863cc1a7ace54364b0_l3.png) —-(3)
—-(3)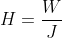
![Rendered by QuickLaTeX.com =left [ frac{R}{J(gamma-1)} right ]left [ T_{1}-T_{2} right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-d976bfeaa8810ac3147fe3e25e46a4e5_l3.png)
![Rendered by QuickLaTeX.com W=-left [ frac{R}{gamma-1} right ]left [ T_{1}-T_{2} right ]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-cd06dd3f1e3f719968f81ce3d0fb491f_l3.png)
![Rendered by QuickLaTeX.com W=-left [ frac{R}{1-gamma} right ]left [ T_{2}-T_{1} right ] ----left ( 4 right )](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-b3078db835607f577fa0f7352f57139d_l3.png)