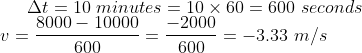AKSHITA MAPARI

Hi, I’m Akshita Mapari. I have done M.Sc. in Physics. I have worked on projects like Numerical modeling of winds and waves during cyclone, Physics of toys and mechanized thrill machines in amusement park based on Classical Mechanics. I have pursued a course on Arduino and have accomplished some mini projects on Arduino UNO. I always like to explore new zones in the field of science. I personally believe that learning is more enthusiastic when learnt with creativity. Apart from this, I like to read, travel, strumming on guitar, identifying rocks and strata, photography and playing chess.

Negative Velocity And Zero Acceleration: How, When, Example And Problems

January 21, 2024January 10, 2022 by AKSHITA MAPARI

In this article, we are going to discuss what causes negative velocity and zero acceleration, how does negative velocity exist, with some examples and problems.

When the system moves in the negative axis of its origin or slows down then the object is moving with negative velocity and if the object decelerates with constant rate then the object is said to have a negative velocity with zero acceleration.

What happens to Acceleration when Velocity is Negative?

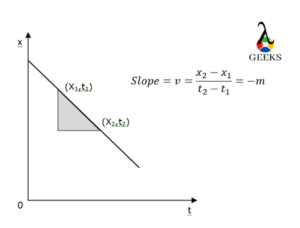
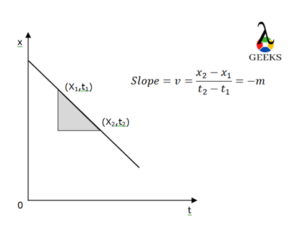
If the displacement of the object is lowered than its initial movement, then the velocity of the object is reduced and measured as negative.

An object moving with negative velocity, which says that the preceding distance covered by the object with time is lowered, then the acceleration of the object is also reducing at the same time and is negative.

Let us elucidate the acceleration of the object moving with a negative velocity with an example. Consider an object slowing down its speed after traveling for a certain distance. After every 20 seconds, the velocity of the object was noted. The initial velocity of the object was 5 m/s and after 20 seconds it was noted that the velocity of an object was reduced to 3 m/s.

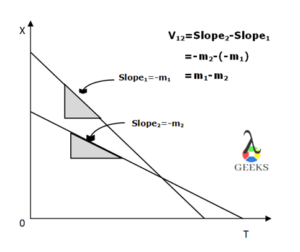
Then, the acceleration of the object is the difference between the final and initial velocity of the object divided by the time interval between which the change has occurred;

a₁=(v₂-v₁)/ΔT=(3-5)/20=-2/20=0.1m/s²

Hence, we can see that the acceleration of the object slowing down is negative as the difference between the final and initial velocity is negative because the initial velocity of the object in motion is greater than that of the final velocity.

If we have a negative velocity of the object throughout its movement, that is, the direction of its displacement is opposite to its motion, then let us see what will be the effect on the acceleration of the object in this circumstance. It is obvious, that the object having negative velocity will reduce its velocity with time as it is decelerating.

Consider an object falling from the hill to the underlying ground area. Let’s say, the initial velocity of the object was -4m/s which then reduced further to -6m/s in 10 seconds then the acceleration of an object will be

a₁=(v₂-v₁)/ΔT==[-6-(-4)]/10=0.2m/s²

Hence, the acceleration of an object will be negative if the velocity of the object is negative. Here, in this example, the velocity is taken as the negative because the displacement of the object is in a negative direction of its motion as it is falling down from the heights.

What is the Example of Zero Acceleration?

The object is said to have zero acceleration if the velocity of the object remains unvaried with time or is at rest.

All the objects at rest or moving with the same initial velocity of the displacement and maintain the same velocity for as long as it is in a motion irrespective of the external forces acting on it, then it is an example of zero acceleration.

Some examples of zero acceleration are, a photon which is a light particle and moves freely at a constant speed without accelerating, an object in space that does not experience the gravitation force and hence floats in the space, an object in a circular motion with its momentum conserved, a rock standing on a hill, a man walking at a constant speed, buoy floating on water, tree, a pole on street, etc.

Conditions for acceleration to be zero

There are two conditions where acceleration can be zero, they are:

Displacement equal to zero.

x=0

For an object at rest, the velocity of the object is zero and hence the acceleration of an object will also be equal to zero.

The initial and final velocity of the object is the same and remains constant.

V_initial=V_final

Well, if the object is in a motion and preserves the constant velocity for all the time then the change in velocity of an object is zero and hence the acceleration is zero.

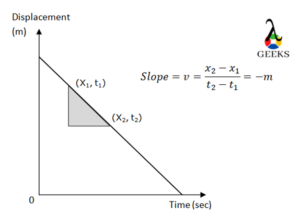
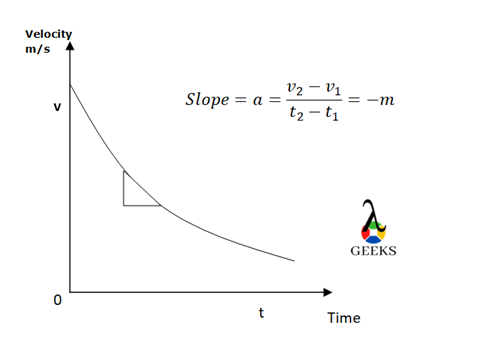
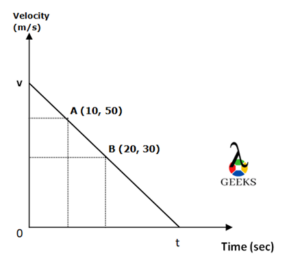
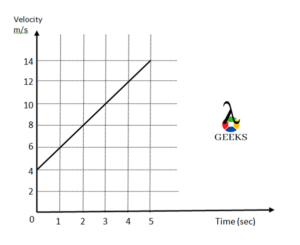
Negative Velocity v/s Time Graph for Zero Acceleration

The acceleration is zero if the velocity of the object is constant.

negative velocity and zero acceleration — **Negative Constant Velocity v/s Time Graph**

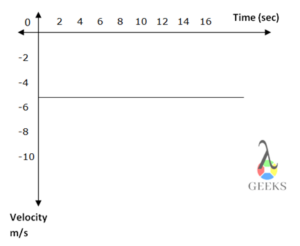
The velocity of the object remains the same and does not vary with time, hence we get a straight line on plotting the graph of velocity versus time graph. If the velocity remains the same, whether it is positive or negative, the acceleration will always be zero.

Can Acceleration be Positive when Velocity is Zero?

The acceleration can be positive or negative based on the variation in the velocity of the object.

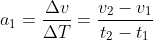
As there is no velocity which implies that the object is stable at rest, there will be no acceleration of the object since the rate of change of velocity found at different time intervals will also be equal to zero as there is no motion of an object.

Well, all the objects in motion do define the speed, velocity, and acceleration too. The object in motion having zero acceleration implies that the object does have acceleration which is equal to zero. This suggests that the object has a uniform acceleration which does not change with time.

The acceleration of the object will be positive only when the object is moving with the positive velocity that is the velocity of the object adds up with time. If an object travels in the reverse direction or reduces its speed with time then the object will have negative velocity and hence the acceleration is negative. It is only when the object is at rest, its velocity will be equal to zero and therefore the acceleration does not exist in this case.

Read on varying acceleration on jolts.

Frequently Asked Questions

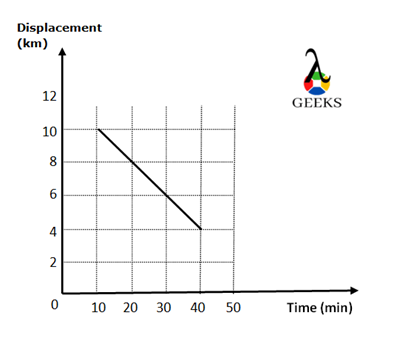
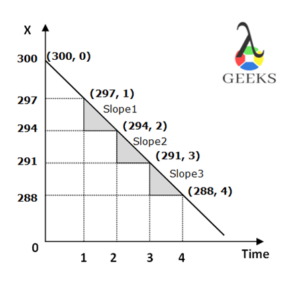
Q1. Consider a car climbing the steeper slope of a mountain, the displacement of a car after every 5 minutes was noted as 50m, 30m, and 15m. Calculate the velocity of a car varied every 5 minutes and hence find the acceleration of a car.

Solution:The displacement of a car in 5 minutes is 50m.

Then the initial velocity of a car for first 5 minutes duration was,

In next 5 minutes, the displacement was 30 m, hence the velocity was

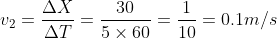
And the final displacement was 15 m in 5 minutes, therefore the velocity was equal to

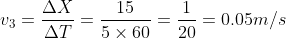
Hence, the acceleration of a car was

The acceleration of a car is very small but negative as the velocity of a car decreases at a minute rate.

Why does the object have zero acceleration?

An object moving at a uniform velocity or remaining at rest will have zero acceleration.

If there is no external force acting on the object that may have resulted in the change of the velocity or the direction of its motion then the object will continue to remain in a uniform motion with zero acceleration.

Also Read:

How To Calculate Negative Velocity: Example And Problems

January 21, 2024January 8, 2022 by AKSHITA MAPARI

Negative velocity is a concept that often confuses students when they first encounter it in physics. However, understanding how to calculate negative velocity is crucial for comprehending the motion of objects in different scenarios. In this blog post, we will explore the meaning of negative velocity, its implications in real-world scenarios, and the methods to calculate negative velocity. So, let’s dive in!

The Meaning of Negative Velocity

What Does Negative Velocity Mean in Physics?

In physics, velocity is a vector quantity that represents the rate of change of an object’s position with respect to time. It consists of two components: magnitude (speed) and direction. When the direction of motion is opposite to the chosen positive direction, the velocity is considered negative. Negative velocity indicates that an object is moving in the opposite direction to the reference point or the chosen positive direction.

The Implication of Negative Velocity in Real-World Scenarios

Negative velocity has various implications in real-world scenarios. Let’s consider an example of a car moving along a straight road. Suppose we choose the forward direction as positive. If the car is initially moving forward with a positive velocity and then begins to slow down and move in the opposite direction, its velocity becomes negative. This change in velocity indicates that the car is decelerating or slowing down.

Calculating Negative Velocity

How to Determine Negative Velocity

how to calculate negative velocity — Image by Jacopo Bertolotti – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

To determine whether velocity is positive or negative, you need to compare the direction of motion with the chosen positive direction. If the object is moving in the opposite direction, the velocity is negative. Conversely, if the object is moving in the same direction as the chosen positive direction, the velocity is positive.

How to Calculate Negative Average Velocity

Average velocity can be calculated by dividing the displacement of an object by the time taken. Displacement is the change in an object’s position, and it can be negative to indicate a change in the opposite direction. Let’s say an object moves from position $x_1$ to position $x_2$ in a time interval $t$ . The average velocity can be calculated using the formula:

$v_{text{avg}} = frac{Delta x}{Delta t}$

If the displacement, $Delta x$ , is negative, it means the object has moved in the opposite direction, indicating a negative average velocity.

How to Find Maximum Negative Velocity

Maximum negative velocity refers to the highest speed an object achieves while moving in the opposite direction to the chosen positive direction. It can be calculated using the formula for average velocity, considering the displacement and time interval. The maximum negative velocity occurs when the object is moving at its highest speed in the opposite direction.

Worked Out Examples on Calculating Negative Velocity

Let’s work through a couple of examples to solidify our understanding of how to calculate negative velocity.

Example 1:
A car moves from position $x_1 = 10 , text{m}$ to position $x_2 = -5 , text{m}$ in a time interval $t = 2 , text{s}$ . Calculate the average velocity of the car.

Solution:
Using the formula for average velocity, we have:

$v_{text{avg}} = frac{Delta x}{Delta t}$

Substituting the given values, we get:

$v_{text{avg}} = frac{-5 , text{m} - 10 , text{m}}{2 , text{s}} = frac{-15 , text{m}}{2 , text{s}} = -7.5 , text{m/s}$

The negative sign indicates that the car is moving in the opposite direction to the chosen positive direction.

Example 2:
An object moves from position $x_1 = -3 , text{m}$ to position $x_2 = 5 , text{m}$ in a time interval $t = 4 , text{s}$ . Find the maximum negative velocity of the object.

Solution:
Again, using the formula for average velocity, we have:

$v_{text{avg}} = frac{Delta x}{Delta t}$

Substituting the given values, we get:

$v_{text{avg}} = frac{5 , text{m} - (-3 , text{m})}{4 , text{s}} = frac{8 , text{m}}{4 , text{s}} = 2 , text{m/s}$

The positive average velocity indicates that the object is moving in the chosen positive direction. Therefore, the maximum negative velocity is 2 m/s, which is the highest speed the object reaches while moving in the opposite direction.

The Relationship Between Negative Velocity and Deceleration

Does Deceleration Have a Negative Sign?

Deceleration refers to the rate at which an object slows down. It can be positive or negative, depending on the direction of acceleration. When an object slows down in the same direction as the chosen positive direction, the acceleration is negative. Conversely, when an object slows down in the opposite direction, the acceleration is positive.

Understanding the Link Between Negative Velocity and Deceleration

Negative velocity and deceleration are closely linked. When an object’s velocity is negative, it indicates that the object is moving in the opposite direction to the positive direction. In this case, if the object is also decelerating, it means that it is slowing down while moving in the opposite direction. The negative velocity and negative acceleration reinforce each other, indicating deceleration in the opposite direction.

What is an example of negative velocity in physics and how can it be calculated?

An example of negative velocity in physics is when an object moves in the opposite direction of a chosen reference point. This means that the object is moving in the opposite direction of the positive direction, resulting in a negative velocity value. For calculating negative velocity, you can use the formula v = (xf – xi) / t, where v is the velocity, xf is the final position, xi is the initial position, and t is the time elapsed. An example illustrating negative velocity in physics can be found at Example of Negative Velocity in Physics.

Numerical Problems on how to calculate negative velocity

Problem 1:

A car is moving in the negative x-direction with an initial velocity of -10 m/s. If it accelerates at a rate of -2 m/s^2 for a time period of 5 seconds, calculate the final velocity of the car.

Solution:

Given:
Initial velocity, $u = -10 , text{m/s}$
Acceleration, $a = -2 , text{m/s}^2$
Time, $t = 5 , text{s}$

We can use the formula for calculating final velocity:
$v = u + at$

Substituting the given values, we get:
$v = -10 + (-2)(5)$
$v = -10 - 10$
$v = -20 , text{m/s}$

Therefore, the final velocity of the car is -20 m/s.

Problem 2:

A ball is thrown upwards with an initial velocity of -15 m/s. The ball decelerates at a constant rate of -3 m/s^2. Calculate the time it takes for the ball to come to rest.

Solution:

Given:
Initial velocity, $u = -15 , text{m/s}$
Acceleration, $a = -3 , text{m/s}^2$
Final velocity, $v = 0 , text{m/s}$

We can use the formula for calculating time:
$v = u + at$

Rearranging the formula to solve for time:
$t = frac{v - u}{a}$

Substituting the given values, we get:
$t = frac{0 - (-15)}{-3}$
$t = frac{15}{-3}$
$t = -5 , text{s}$

Therefore, it takes 5 seconds for the ball to come to rest.

Problem 3:

A train is initially moving with a velocity of -20 m/s. It accelerates at a rate of 4 m/s^2 for 10 seconds and then decelerates at a rate of -2 m/s^2 for 5 seconds. Calculate the final velocity of the train.

Solution:

Given:
Initial velocity, $u = -20 , text{m/s}$
Acceleration during the first 10 seconds, $a_1 = 4 , text{m/s}^2$
Acceleration during the next 5 seconds, $a_2 = -2 , text{m/s}^2$
Time during the first acceleration, $t_1 = 10 , text{s}$
Time during the next deceleration, $t_2 = 5 , text{s}$

We can calculate the final velocity using the formula:
$v = u + (a_1 cdot t_1) + (a_2 cdot t_2)$

Substituting the given values, we get:
$v = -20 + (4 cdot 10) + (-2 cdot 5)$
$v = -20 + 40 - 10$
$v = 10 , text{m/s}$

Therefore, the final velocity of the train is 10 m/s.

Also Read:

Negative Velocity And Negative Acceleration: Why, How, Graph, Example And Detailed Facts

January 21, 2024January 7, 2022 by AKSHITA MAPARI

In this article, we are going to discuss about the dependency of the negative velocity and negative acceleration on each other with some examples and graphs.

If the object shifts in the direction opposite to its mobility then the velocity of the object is negative. The acceleration of the object is found to be negative if the velocity of an object decreases with time.

What is Negative Velocity?

A negative velocity is a ratio of the displacement of an object in a direction away from its direction of motion.

If the direction of motion of an object is opposite then the displacement then the velocity of the object is negative.

The velocity is given by the equation

v=(Δx/Δt)=(x₂-x₁)/(t₂-t₁)—(1)

For velocity to be negative in the above equation (1),

x₂>x₁

The final displacement of the object should be less than the initial displacement.

What is Negative Acceleration?

An object slowing down with time will show the reduction in the velocity of the object with time and distance.

An object is said to be accelerating if there is a change in the velocity of an object during its motion. The velocity of an object varies and lowers along with the displacement, the speeding down of an object will lower the acceleration of an object.

a=(Δv/Δt)=(v₂-v₁)/(t₂-t₁)

For acceleration to be negative in the above equation (2),

v₂>v₁

For acceleration to be negative, the initial acceleration of an object should be greater than the velocity of the object on further accelerating.

Can you have Negative Velocity and Negative Acceleration?

This is possible in the case of an object slowing down its speed, or falling from a greater height, or moving away from the original direction of motion, reversing its direction.

If the position of an object changes away from its direction of motion and velocity decreases with time, then the object has negative velocity and negative acceleration both.

We can consider a simple example of a comet approaching the Sun from afar nebula by attracting towards the gravitational force of the Sun. But as it approaches near the Sun, it gains potential energy and diverts back from its direction of motion, and accelerates away from the Sun in a parabolic path.

As the comet is far from the Sun, its speed is about 2000 miles per hour, once it reaches near the Sun its speed becomes nearly 100000 miles per hour due to the external gravitational pull of the Sun on the comet. On deflecting from the Sun, its speed is even high and decreases as the distance from the Sun increases.

Hence the velocity of the comet is actually negative while traveling away from the Sun and hence the acceleration is also negative as the velocity decreases with time.

Read more on comets.

Negative Velocity Negative Acceleration Graph

To measure the velocity of the object, we have to plot a graph of displacement of an object at different time duration. The following is a position-time graph of a decelerating object.

negative velocity and negative acceleration — **Position-Time Graph**

The graph shows that the displacement of an object is in a reverse direction and the position of an object from its origin decreases with time. On finding the slope of a position-time graph, you will find the velocity of the graph. In the above graph, the velocity of the object decreases with time and hence the velocity is calculated to be negative.

To find out the acceleration of an object, we plot a graph of velocity v/s time rate of change of velocity. The graph is as follows:

From the graph, we can see that the velocity linearly drops with time. The slope of a graph gives the acceleration of an object. Since the velocity reduces with time, the acceleration is negative.

If the object accelerates at a higher velocity than the previous, then we will have a positive slope of a graph and hence a positive acceleration.

Negative velocity and negative acceleration example

Consider an airplane traveling at a speed of 850 km/h accelerates at a lower altitude to a speed of 580 km/h and then speeds down to the surface of the Earth lowering its speed during its landing. The horizontal velocity of the plane is deduced while the vertical velocity also decreases while the plane is landing on the ground.

Here, in this case, the distance between the airplane and the landing area decreases with time. Initially, the airplane was flying at a height of 10,000 meters above the surface and then follows the lower altitude at a height of 8000 meters in 10 minutes. Then the velocity can be calculated as the change in position with respect to the initial position and the time given by the equation

v=(x₂-x₁)/(t₂-t₁)

Here, x₁=10000 meters, x₂=8000 meters,

Hence, the velocity of the plane while coming down to the lower altitudes is -3.33 m/s. It is seen that as the height of the plane decreases its velocity is calculated and found out to be negative.

The acceleration of a plane is a varied velocity with time, given by the relation

a=(v₂-v₁)/Δt

The initial velocity of the airplane was 850km/h which was then reduced to 580km/h. Hence, the acceleration of the plane with decreasing velocity is

We have v₁=850 km/h, v₂=580 km/h, Δt=600 seconds

a=(580-850)/600=-270/600=-0.45m/s²

Since the velocity decreases with time, the acceleration becomes negative.

How Negative Velocity and Negative Acceleration Works?

The velocity is directly related to the change in the displacement whereas the acceleration of the object depends upon the change in its velocity.

The negative velocity reverses the direction of the object as the displacement is in the negative axis of the system while the speed of the object is reduced due to negative acceleration.

The negative velocity pulls back the object in a direction opposite to its motion and the negative acceleration slows down the speed of an accelerating object and hence it decelerates.

The object falling on the ground from a certain height converts the potential energy to the kinetic energy utilized to displace itself from the height to the ground surface. The height of the object from the ground from where its flight was initially started decreases. Compatibility, the velocity of the object is negative as the displacement of an object is in a negative axis.

Suppose we throw an object in a projectile motion, the velocity of the object on reaching the highest height reduces once all the kinetic energy of the object is converted back into the potential energy of the object.

From here the velocity of the object initially increases as the potential energy is converted into kinetic energy and due to the gravitational force acting on the object, and then slightly decreases the velocity while accelerating downward and deducts sharply when it reaches near the surface of the Earth.

As the velocity decreases with time, the difference in the preceding and the initial velocity is negative and hence the acceleration of the object is negative.

When Velocity is Negative and Acceleration is Negative what is happening to the Object?

When the velocity is negative of the object the displacement is in the reverse direction and when acceleration is negative the speed of the object accelerating is reduced.

As the velocity and as well as the acceleration of the object decreases, the kinetic energy of the object is converted into the potential energy of the object. We can even consider that there is some external impact on the object due to which the velocity of the object lowers.

Frequently Asked Questions

Q1. How does the graph of velocity v/s time for the comet approaching the Sun and then deflecting back will look like? Explain the graph for the same regarding velocity and acceleration.

The speed of the comet while approaching the Sun from the far distance is around 2000km/h, and increases as the gravitational pull on the comet increases with decreasing distance

The speed becomes approximately 1L km/h when it is near the Sun. Hence, the change in velocity of the comet is positive and therefore the acceleration of the comet is also positive as shown in the graph below.

It receives the energy from the sun and sweeps back against the gravitational pull of the Sun gradually decreasing its velocity as it elapses the distance away from the Sun. Initially, there will be a major fall in the velocity as the comet will lose its extra energy received from the radiation of the Sun quickly.

Since the velocity of the comet decreases the acceleration of the comet is negative and the same is shown in the graph where the velocity is sloping down with time.

Q2. Consider an object slowing down, base on the displacement of an object away from its original position with time the velocity was calculated and plotted for the same time interval. The graph is shown below. Based on the following graph calculate the acceleration of the object when time is equal to 5 seconds.

Solution: From the above graph, the velocity of the object at time t=5seconds, the velocity of the object was v=-20 m/s.

The velocity is the product of the acceleration of the object during that time.

Hence, the acceleration of the object is

Therefore, the acceleration rate of an object at time t=5 seconds was -4m/s².

Is negative acceleration the same as the deceleration of the object?

The acceleration of the object is negative if the velocity of the object is lowering with time.

If the velocity of the object along with the distance decreases, then the object is said to be decelerated with time. The decelerating object accompanies with negative acceleration.

Why does the velocity of a falling object from the height be negative?

If the object moves in a reverse direction then the difference between the final and initial displacement is negative.

Since the displacement of a falling object is in a reverse direction, its velocity and hence the acceleration will be negative.

Is it possible to measure the distance covered by an object from its velocity-time graph?

Yes, the displacement of an object can be found from the velocity-time graph.

Since velocity is defined as a distance elapsed by the object in a given time, then distance will be equal to the velocity of the object during that time and the time duration at which the velocity was noted.

Also Read:

7 Negative Velocity Example: Examples And Problems

January 21, 2024January 6, 2022 by AKSHITA MAPARI

In this article, we are going to discuss some negative velocity examples and solve related problems.

Some examples of negative velocity are as follow:-

Object falling down

An object accelerating down from greater heights to down the surface decreases its position while accelerating. Since the position decreases with time, the velocity of the object is negative.

The energy of the object is always conserved; it only changes from one form of energy to another. While the object accelerates upward its kinetic energy utilized for its drift is converted into potential energy and once all the kinetic energy is converted into the potential energy, the object starts accelerating down to zero potential surfaces.

Since the energy is conserved in the form of the potential and kinetic energy of the object falling from the heights, its initial energy produced will be equal to the final energy.

KE₁+PE₁=KE₂+PE₂

1/2 mu₁²+mgh₁=1/2 mv₂²+mgh₂

1/2 u₁²+gh₁=1/2 v₂²+gh₂

u₁²+2gh₁=v₂²+2gh₂

u₁²-v₂²=2g(h₂-h₁)

v₂²=u₁²-2g(h₂-h₁)

v₂=√u₁²-2g(h₂-h₁)

In short, kinetic energy is equal to the potential energy of the object

1/2 mv²=mgh

v²=2gh

v=√2gh

This implies that the velocity of the object during its flight in the air depends upon the height at which it is above the surface of the ground.

As the height of the falling object decreases, the velocity of the object will decrease by the square root of its height. Hence the velocity of an object is negative in this case.

Slipping of feet while trying to climb up the slider

You must have noticed that due to lack of frictional force on the slider, we repeatedly slide backward while climbing up the slider from the slide. This reduces the velocity of a person while climbing and often sliding back to the ground. Hence, this is also an example of a negative velocity.

Object slowing down

The fast accelerating object suddenly lowers its velocity then we have an exponential decrease in the velocity of the object.

negative velocity example — **Graph of an object decreasing its velocity with time**

For such objects, the acceleration will also be negative.

An object moving in a reverse direction with high speed

While moving in a reverse direction from the original point then the position of the object with respect to the origin will decrease, hence the velocity of the object which is a change in position with time will be negative.

When the object takes sharp reverse acceleration, then the acceleration is positive but the velocity of the object is negative.

Kingfisher diving in a river for fish

A bird, kingfisher diving into the river water to catch the fish for its food moves with negative velocity as it comes near the surface of the water from the height at which it was flying.

Light traversing through the medium

As light travels from one medium to another, the speed of light changes. On entering the denser medium the speed of light rays decreases, hence is also an example of negative velocity, because the distance elapses by the light in the air in one second is more as compared to its velocity in the denser medium, as it travels slower comparably.

Read more on the speed of light.

Spring

Spring always tries to regain its original size upon stretching. If a heavy mass is attached to one end of the spring comparable to its spring constant and keeping the other end fixed, upon stretching the spring by pulling a mass on a horizontal slide, it will build potential energy which will be converted into kinetic energy once it is released.

The mass will travel in a reverse direction due to equal and opposite reactions and will displace at a position towards the fixed point and remain stable. This is an instantaneous process. Since the position decreases with time the velocity is negative.

Flow of current

The direction of a flow of current is in the direction opposite to the motion of electron charges; this also can be accounted for a negative velocity of electrons compared to the direction of the current.

Solved Problems

Problem 1: A car travels a distance of 7km in 7min and then slows down on reaching the district road and travels 3km in 9minutes. Calculate the change in velocity.

Solution: A car displaces 7 km from the original point, x₁=7km, time taken t₁=7min;

Hence the speed of the car is

v₁=x₁/t₁=7* 60/7=60km/h

A car travels 3 km in 9 minutes, hence the speed of the car is

v₂=x₂/t₂=3*60/9=20km/h

Hence change in velocity is

V=V₂-V₁=20-60=-40km/h

The change in the velocity of the car becomes negatives once it slows down.

Problem 2: A weight of mass 1kg is kept on a horizontal slide made up of glass. A weight is attached to a spring of length 1 meter whose other end is sealed in a wall. A mass is pulled to a distance of 50 cm away from its position on applying a force and relieved. After which the weight displaces 80 cm in a second and rests at a position 80 cm away from the wall.

Find the instantaneous velocity of a mass and the potential energy of spring on pulling the mass. Also, calculate the potential energy stored in the spring when it was displaced at a distance of 50 cm from its resting position. Given the spring constant k=1.5.

Solution:

Given: x₁=50cm, x₂=80cm, t₁=0, t₂=1sec;

Instantaneous\ Velocity=x₂-x₁/t₂-t₁=50-80/1-0=-30cm/s=-0.3m/s

Velocity of a weight is -0.3m/s which are negative because the weight displaces in the reverse direction.

Problem 3: Find the average velocity of an object traveling with time. The distance elapsed by the object at different times was noted, the same is shown in the following table. Plot the graph for the same.

Displacement(km)	Time(min)
10	10
8	20
6	30
4	40

Solution: The position-time graph for the above data is as below

**Position time graph** **for the object**

Change in velocity with respect to time is equal to the slope of the graph.

v₁=x₂-x₁/t₂-t₁=8-10/20-10=-2/10=-2*1000/10*60m/s=-3.3m/s

v₂=x₂-x₁/t₂-t₁=6-8/30-20=-2/10=-2*1000/10* 60m/s=-3.3m/s

v₃=x₂-x₁/t₂-t₁=4-6/40-30=-2/10=-2*1000/10*60m/s=-3.3m/s

v₄=x₂-x₁/t₂-t₁=4-8/40-20=-4/20=-4*1000/20*60m/s=-3.3m/s

It is seen that the velocity of the object remains constant but the position of the object decreases with increasing time, hence the velocity of the object is negative.

The potential energy of a spring is half time the spring constant and a square of the displacement.

U=1/2kx²

=1/2*1.5*0.5²

=1/2*1.5*0.25

=0.19 Joules

Hence, the energy stored in the string was 0.19 Joules.

Problem 4: A girl walks 100meters towards North in 1minute and returns back to the point from where she had started and walks 200meters towards South from there in 4minutes. Calculate her actual velocity and displacement to reach that point where now she is.

Solution: A girl walks 100meters initially towards North in 1minute hence her walking speed was

Speed=Distance/Time

v₁=100/60=1.67m/s

Then, a girl covers 200meters in 4minutes, therefore the velocity of a girl is

v₂=200/4*60=0.83m/s

Therefore, the velocity of a girl in 5minutes is

V=V₂-V₁=0.83-1.67=-0.84m/s

And actual displacement of a girl from original position is

x=x₂-x₁=200-100=100meters

That is 100 meters towards the South from the original position.

Problem 5: What is the velocity of an object when it is at a height of 10 meters above the ground and how does the velocity of the object vary at what rate?

Solution: The velocity of the object during its flight in the air is proportional to the square root of its height from the ground and the acceleration due to gravity of the Earth given by the relation

v=√2gh

When the object is at a height of 10 meters, it velocity will be equal to

v=√2*9.8*10=√196=14 m/s

When h=9m

v=√2*9.8*9=√176.4=13.28 m/s

When h=8m

v=√2*9.8*8=√156.8=12.52 m/s

When h=7m

v=√2*9.8*7=√137.2=11.71 m/s

When h=6m

v=√2*9.8*6=√117.6=10.84 m/s

When h=5m

v=√2*9.8*5=√98=9.8 m/s

When h=4m

v=√2*9.8*4=√76=8.7 m/s

When h=3m

v=√2*9.8*3=√58.8=7.67 m/s

When h=2m

v=√2*9.8*2=√39.2=6.26 m/s

When h=1m

v=√2*9.8*1=√19.6=4.43 m/s

Height (m)	Velocity(m/s)	Acceleration
10	14	-0.72
9	13.28	-0.76
8	12.52	-0.81
7	11.71	-0.87
6	10.84	-1.04
5	9.8	-1.10
4	8.7	-1.03
3	7.67	-1.41
2	6.26	-1.83
1	4.43	-4.43

This indicates that, as the height decreases, the velocity of an object decreases, and hence acceleration also decreases. The acceleration of the object sharply decreases when it is near the ground surface.

Problem 6: A ray of light enters a bucket of water and passes through a glass slab placed in it. Find the velocity of the light rays in each medium. The refractive index of water is 1.3 and that of glass is 1.5.

Solution: RI of water is n=1.3,

n=c/v

v=c/n=3⊓*10⁸*1.3

v=2.3*10⁸m/s

Now the velocity of light is 2.3*10⁸m/s. Hence, the speed of light in glass is

n=v₁/v₂

v₂=v₁/n=2.3*10⁸/1.5

v=1.5*10⁸m/s

Hence the velocity of light in glass is *10⁸m/s.

Frequently Asked Questions

Why velocity is negative?

Velocity is defined as a change in the position of an object with different time intervals.

If the position of an object shifts with time, the difference in position with respect to its previous position will be negative and hence velocity will be negative compared to the preceding interval.

How phase velocity of light can be negative?

Distance traveled by a single ray of light or single wave in one second of time is called phase velocity.

Negative velocity comes into a scene while light travels from one medium to another because the speed of light decreases on entering the denser medium.

Also Read:

Negative Velocity Graph: Different Graphs And Their Explanations

January 21, 2024January 5, 2022 by AKSHITA MAPARI

In this article, we are going to discuss negative velocity along with graphs and solve problems to understand various facts of negative velocity.

If the velocity of an object decreases with respect to time duration then the object is said to have a negative velocity that might be constant, varying, instantaneous, or relative to the direction of the velocity of some other object into consideration.

Constant Negative Velocity Graph

If the slope of the position v/s time graph is negative and the distance decreases at a constant rate along with time, then it is said to be a constant negative velocity graph.

If ‘m’ is a value equal to the slope of the graph, which is linear and remains the same on calculating the slope between any two points on the line then the velocity is constant. Since the distance abates with time, the slope is negative and hence the velocity is negative.

Problem 1: Consider a pulley ties with two masses on both the ends of the rope of length 30meters, the mass on one end of the rope is pulled to raise another mass tied on another end of the rope at a constant rate. If 10meters of the rope was pulled in the first 12seconds and 20meters of ropes in the next 24seconds, then calculate the velocity of the mass tied on another end.

Solution: Since the change in length of the rope on one side in 12seconds is from say 0 to 10 meters and at the same time length of the rope has decreased to 30-10=20meters on another end of the rope.

Now the length of the rope is 20meters, so, after pulling 20meters of rope in 24seconds, the length of the rope on the other side is 20-20=0meters.

Hence, we have: x₁=30m, x₂=20m and x₃=0

Time t₁=0, t₂=12 seconds, t₃=12+24=36seconds

Therefore,

Slope₁=x₂-x₁/t₂-t₁=20-30/12-0=-10/12=-0.8m/s

Slope₂=x₃-x₂/t₃-t₂=0-20/36-12=-20/24=-0.8m/s

Slope₃=x₃-x₁/t₃-t₁=0-30/36-0=-30/36=-10/12=-0.8m/s

It is clear that

Slope₁=Slope₂=Slope₃=-0.8m/s

Hence the slope is linear and has constant negative velocity.

Negative Uniform Velocity Graph

When the object covers equal distance in equal intervals of time then the object is said to have uniform velocity, and if the object traverses back in a uniform velocity then the object is moving with negative uniform velocity.

negative velocity graph — **Negative Uniform Velocity Graph**

As the object displaces an equal distance in an equal interval of time, it implies that the velocity of the object is constant and hence there is no acceleration of the object.

Problem 2: Supposed, a narrow road runs from a village from point A to B such that only one car can travel on the road at a time. The length of the narrow road is 1km long. A carA travels a distance of 300meters from a narrow road from point A and encounters carB, hence starts reversing back at a constant speed and covers 3meters per second. Plot a graph and find the velocity at 3 different points.

Solution: The displacement of the car is 3meters per second and the distance from pointA decreases at the rate of 3m/s. A CarA had covered a distance of 300meters and will traverse back 300meters at a rate of 3m/s.

Position(x meters)	Time(t sec)
300	0
297	1
294	2
291	3
288	4
285	5

Table showing position of an object varied with time

We plot a graph for displacement v/s time,

Slope₁=x₂-x₁/t₂-t₁=294-297/2-1=-3/1=-3m/s

Slope₂=x₃-x₂/t₃-t₂=291-294/3-2=-3/1=-3m/s

Slope₃=x₃-x₁/t₃-t₁=288-291/4-3=-3/1=-3m/s

Slope₁= Slope₂= Slope₃=-3 m/s

The slope is constant and negative, and hence the velocity of the car taking a reverse on a narrow road is -3m/s.

Negative Relative Velocity Graph

Velocity is a vector quantity and relative velocity is a vector difference of velocities of two bodies. That is if the velocity of object A is V_a and that of object B is moving with velocity V_b, then the relative velocity of both the objects with respect to each other is V_ab=V_a-V_b.

On finding the slope of position v/s time plot, we can calculate the relative velocity of the object with respect to each other. If both the objects are decelerating then the slope of the graph will be negative.

Problem 3: A car traveling with a velocity of 60km/hr crosses a woman walking on a street with a speed of 2m/s in the same direction. What is their relative speed?

Solution: V₁=60 km/h=60*1000/60*60=16.67m/s

V₂=2m/s

Hence, the relative velocity of the car with respect to a lady is

V=V₁-V₂=60-2=58m/s

The relative velocity of the car will be 58m/s and that of the woman will be –58m/s as the speed of a car is faster than the woman.

Negative Velocity Positive Acceleration Graph

If the object accelerates back from its original position along with time by changing the velocity of the object then we have negative velocity but the acceleration of the object is positive.

The object accelerating backward changes its velocity frequently, that is the rate of displacement of the object in a time interval is not constant and hence the graph shows different slopes on plotting the position of the object at different times.

If the velocity of the object decreases at an exponential rate then we get the positive acceleration from the negative velocity of the object. Let us illustrate this with the problem below.

Problem 4: Consider the same situation given in problem No.2 and the same car is accelerating backward decreasing its speed. Suppose the covers first 200 meters with a speed of 40 km/h and next 50 meters with a speed of 15 km/h and remaining distance in 10 km/h speed. Then calculate the velocity and acceleration of the car at different points.

Solution: A car initially was at say point X₁= 300 and travels 200 meters to reach point X₂= 100 with velocity V₁=40 km/h. From where the velocity of the car changes to V₂=15 km/h and travels next 50 meters and velocity slightly drop to 10 km/h and comes at the original position on traveling 50 meters on the same speed.

**A Car accelerating in Reverse Direction**

The time taken to elapse 200 meters with the speed of 40 km/h is

t₁=Distance/Speed=200*60*60/40*1000=18 seconds

Time taken to cover 50 meters with a speed of 15 km/h is

t₂=Distance/Speed=50*60*60/15*1000=12 seconds

And a time taken to cover a distance of 50 meters with a speed of 10 km/h is

t₃=Distance/Speed=50* 60*60/10*1000=18 seconds

Therefore, T₁=18 seconds, T₂=18+12=30 seconds, T₃=30+18=48 seconds

Since the acceleration is define as the change in the velocity of a car in different time intervals, hence,

a₁=v₂-v₁/Time Interval=40-15/18=25*1000/18*60* 60=0.38 m/s²

a₂=v₂-v₁/Time Interval=15-10/12=5*1000/12*60*60=0.12 m/s²

a₃=v₂-v₁/Time Interval=10-0/18=10*1000/18*60*60=0.15 m/s²

This gives the positive acceleration. At the steeper slope of graph, the acceleration is of a car is higher and at gentle slope the acceleration is smaller.

Instantaneous Velocity Negative Graph

The object is said to have an instantaneous velocity when it displaces from its place drastically. If the displacement is in a reverse direction then it is said to have instantaneous negative velocity.

Here, the displacement of the object is seen suddenly in a short span of time and hence the instantaneous velocity is high.

This is seen in the case of spring tied with a mass at one end having its own potential and another end of the spring is held fixed on the rigid wall. When the mass is pulled away from the spring, the spring potential energy is built and the spring force pulls back the mass towards it to regain its original size by converting this potential energy into kinetic energy.

If the mass is heavy, then after releasing the mass attached to the spring, the spring force displaces the mass towards the rigid wall. The mass will resist the spring force and makes its place there. Hence, the position of the mass varied, and the distance separating it from the rigid wall decreased.

Since the displacement decreases, we have negative velocity in the picture.

Problem 5: If the mass of 2kg is attached to a string of length 1.5 meters at one end and another end is fixed at a rigid wall. On pulling the 50 cms away from its position linearly and released, the mass displaces towards the wall and remains stable at 80 cm away from the wall. Find the instantaneous velocity of the mass if the mass came to its resting position in 1 second.

Solution: A mass is displaced 150 – 80 =70cms =0.7m from its original position and has covered a distance of 70+50 =120cms =1.2m on releasing the spring.

Instantaneous velocity =Displacement/Time taken=1.2 m/1 second=1.2 m/s

Hence, the mass is displaced with a velocity of 1.2 m/s.

Negative Velocity v/s Time Graph Displacement

The velocity is a ratio displacement in a specific time duration, given by the relation

Velocity=Displacement/Time

Hence, the displacement of an object in time ‘t’ moving with velocity ‘v’ is

x=vt

The displacement of the object at a point or at a certain time can be calculated by multiplying it with the velocity of the object at that time.

Problem 6: Based on the following graph calculate the distance between points A & B.

Solution: Distance of Point A from the origin is

x₁=v₁t₁=10* 50=500m

The distance between point B and the origin is

x₂=v₂t₂=20*30=600m

Hence, the distance between point A & point B is

x=x₂-x₁=600-500=100m

Therefore, point B is 100 meters away from point A.

Read More on Negative Refraction.

Negative Slope Velocity Time Graph

The slope of the velocity-time graph will be negative only when the velocity of an object traveling decreases along with time.

If the slope of the velocity-time graph is negative, it means the acceleration is negative.

Problem 7: Find the average acceleration of a swing whose velocity is decreased with time as shown in the table.

Velocity(m/s)	Time(seconds)
8	1
6	5
4	10
2	15

Solution: Let’s calculate the acceleration at different time intervals

a1=v₂-v₁/t₂-t₁=4-8/10-1=-4/9=0.44 m/s²

a2=v₂-v₁/t₂-t₁=2-6/15-5=-4/10=0.40 m/s²

a3=v₂-v₁/t₂-t₁=6-8/5-1=-2/4=0.5 m/s²

a4=v₂-v₁/t₂-t₁=4-6/10-5=-2/5=0.40 m/s²

Hence, the average acceleration is

aˉ=a₁+a₂+a₃+a₄/4

aˉ=0.44+0.4+0.5+0.4/4=0.435 m/s²

Negative Displacement Velocity Time Graph

If the object is taking a reverse turn from its original position with decreasing velocity along with time then we get negative displacement velocity on plotting the same on a graph. The same is demonstrated in the graph below.

Since the velocity of the object is equal to the displacement of the object it makes in time duration, the displacement can be calculated as a product of the velocity of the object into time.

Problem 8: Consider the above velocity-time graph; the object is decelerating with time. Based on the above graph calculate the displacement of the object at a time= 5 seconds.

Solution: AT time t=5seconds, v=-20 m/s.

Velocity =Displacement/Time

x=vt

x=-20*5=-100m

Hence the displacement of an object is -100 meters from origin.

How to Calculate Distance from Negative Velocity Time Graph?

Since the velocity of the object is determined by the distance it covers in a specific time, the displacement of the object is a product of its velocity into time.

Velocity =Displacement/Time

x=vt

The displacement from the velocity-time graph is the area covered by the curves in the graph. For negative velocity the displacement will also be calculated and found to be negative, henceforth the displacement of the object with respect to its original position can be known.

Lets us see, how to calculate the displacement from the negative velocity-time graph through an example.

Problem 9: Consider the following velocity-time plot of an object, based on it calculate the displacement of an object and its position from its original position.

Solution: The area of the triangle in first quadrant is

Area of triangle =1/2 bh

x₁=1/2*10* 7=35m

The area of the triangle in fourth quadrant is

x₂=1/2*12* (-8)=-48m

Hence, the total displacement of an object is

x=x₁+x₂=35-48=-13m

This implies that the object has been displaced 13 meters further from the original position.

This is how the displacement is calculated from the velocity-time graph.

Frequently Asked Questions

How will you plot a graph from an object accelerating at a speed of 2m/s with its initial velocity of 4m/s?

Given: a=2m/s, u=4m/s

Velocity and time relation is given by the formula

v=u+at

At time t=0,

v=4+2*0=4m/s

At time t=1,

v=4+2* 1=4+2=6m/s

At time t=2,

v=4+2*2=4+4=8m/s

At time t=3,

v=4+2*3=4+6=10m/s

At time t=4,

v=4+2*4=4+8=12m/s

At time t=5,

v=4+2* 5=4+10=14m/s

Time(sec)	Velocity(m/s)
0	4
1	6
2	8
3	10
4	12
5	14

Plotting the graph of the same,

How to find acceleration from a velocity–time graph?

Acceleration is a rate of change of velocity at different time intervals.

Hence the slope of a graph of velocity v/s time will give the acceleration of the body.

Also Read:

How To Find Velocity Without Time: Facts, Problems

January 20, 2024January 4, 2022 by AKSHITA MAPARI

Finding velocity without knowing the time may seem like a challenging task, but it is indeed possible. In this blog post, we will explore various methods to determine velocity without time. We will delve into the concept of velocity and understand why time is crucial in calculating it. We will also discuss special cases and common misconceptions related to finding velocity without time.

How to Find Velocity without Time

Understanding the Concept of Velocity

Before we dive into the methods of finding velocity without time, let’s first understand what velocity is. velocity is a vector quantity that measures the rate of change of an object‘s position with respect to time. It includes both the speed and direction of an object. Speed, on the other hand, is a scalar quantity that only measures the rate of change of distance traveled by an object.

The Importance of Time in Calculating Velocity

time plays a crucial role in calculating velocity. When we know the time taken by an object to travel a certain distance, we can easily determine its velocity using the formula:

$text{Velocity} = frac{text{Distance}}{text{Time}}$

However, there are situations where we may not have access to the time component, making it necessary to find velocity using alternative methods.

Methods to Determine Velocity without Time

Using Distance and Acceleration

One way to find velocity without time is by using the distance traveled and the acceleration of the object. If we know the initial and final velocities of the object, we can use the following formula:

$text{Velocity}^2 = text{Initial Velocity}^2 + 2 times text{Acceleration} times text{Distance}$

This equation is derived from the kinematic equation, (v^2 = u^2 + 2as), where (v) is the final velocity, (u) is the initial velocity, (a) is the acceleration, and (s) is the distance traveled.

Let’s consider an example to illustrate this method. Suppose an object starts from rest (initial velocity = 0) and undergoes constant acceleration of 5 m/s². If it travels a distance of 100 meters, we can find the velocity using the formula:

$text{Velocity}^2 = 0^2 + 2 times 5 times 100$

$text{Velocity}^2 = 1000$

$text{Velocity} = sqrt{1000}$

$text{Velocity} = 31.62 , text{m/s}$

In this example, we were able to find the velocity without knowing the time it took.

Using Initial and Final Velocity

Another method to find velocity without time is by using the initial and final velocities of the object. If we know the acceleration, we can use the following formula:

$text{Velocity} = frac{text{Final Velocity} - text{Initial Velocity}}{text{Time}}$

However, since we don’t have the value of time, we can modify the formula as follows:

$text{Velocity} = frac{text{Final Velocity} - text{Initial Velocity}}{text{Acceleration}}$

Let’s consider an example to illustrate this method. Suppose an object starts with an initial velocity of 10 m/s and undergoes constant acceleration of 2 m/s². If the final velocity is 30 m/s, we can find the velocity using the formula:

$text{Velocity} = frac{30 - 10}{2}$

$text{Velocity} = 10 , text{m/s}$

In this example, we were able to determine the velocity without knowing the time.

Using Angular Velocity and Acceleration

In certain cases involving rotational motion, we can find the velocity without time by using angular velocity and acceleration. Angular velocity measures the rate of change of angular displacement with respect to time. If we know the angular acceleration and the distance traveled, we can use the following formula:

$text{Velocity} = sqrt{2 times text{Acceleration} times text{Distance}}$

Let’s consider an example to illustrate this method. Suppose a wheel undergoes angular acceleration of 10 rad/s² and covers a distance of 5 revolutions. If we convert revolutions to radians (1 revolution = 2π radians), we can find the velocity using the formula:

$text{Velocity} = sqrt{2 times 10 times (5 times 2pi)}$

$text{Velocity} = sqrt{200pi}$

$text{Velocity} approx 25.13 , text{m/s}$

In this example, we were able to determine the velocity without knowing the time by utilizing angular velocity and acceleration.

Special Cases in Finding Velocity without Time

Image by Pradana Aumars – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

Finding Constant Velocity without Time

In the case of an object moving with constant velocity, the velocity remains the same throughout its motion. Therefore, if we know the initial velocity, we can directly use it as the velocity without the need for time. This applies to scenarios where there is no acceleration or the net acceleration is zero.

Finding Horizontal Velocity without Time

When an object is in projectile motion, its horizontal velocity remains constant throughout the motion. This means that even without knowing the time, we can use the initial horizontal velocity as the velocity of the object.

Finding Tangential Velocity without Time

In cases involving circular motion, tangential velocity is the velocity of an object traveling along the tangent to the circular path. If we know the radius of the circle and the angular velocity, we can find the tangential velocity without the need for time. The formula to calculate tangential velocity is:

$text{Tangential Velocity} = text{Angular Velocity} times text{Radius}$

How can I find the horizontal velocity without knowing the time?

If you are trying to determine the horizontal velocity of an object without knowing the time, you can use the concept of projectile motion. Projectile motion involves the motion of an object in the absence of external forces, where its motion in the vertical and horizontal directions are independent of each other. To find the horizontal velocity, you can use the equation v = d / t, where v represents the velocity, d is the horizontal distance traveled, and t is the time. By rearranging the formula as t = d / v, you can solve for time. However, if you desire to find the horizontal velocity without time, you can refer to the article “How to Find Horizontal Velocity”. It covers the necessary steps to calculate horizontal velocity using information such as the launch angle, initial velocity, and gravitational acceleration.

Common Misconceptions and Challenges in Finding Velocity without Time

How To Find Velocity Without Time: Facts, Problems 45

One common misconception is that velocity can always be determined without time. However, as we have seen, this is only possible when certain conditions are met, such as constant velocity, constant acceleration, or specific cases like projectile or circular motion. It is essential to understand the underlying concepts and apply the appropriate methods accordingly.

Another challenge in finding velocity without time arises when dealing with situations that don’t fall into the predefined categories. In such cases, it may be necessary to gather more information or use alternative approaches to determine the velocity accurately.

Finding velocity without knowing the time can be achieved through various methods, such as using distance and acceleration, initial and final velocity, or angular velocity and acceleration. It is crucial to understand the underlying concepts and apply the appropriate formulas accordingly. However, it is important to note that finding velocity without time is not always possible, and specific conditions must be met. By mastering these methods and understanding the limitations, we can effectively calculate velocity even in situations where time is unknown.

Also Read:

How To Find Velocity With Acceleration: Different Approaches, Problems, Examples

January 21, 2024January 2, 2022 by AKSHITA MAPARI

Velocity and acceleration are fundamental concepts in physics that describe the motion of an object. Velocity measures the rate at which an object changes its position, while acceleration measures the rate at which an object changes its velocity. In this blog post, we will explore various methods to find velocity with acceleration, including calculating velocity with given acceleration and time, finding velocity with acceleration and initial velocity, determining velocity when acceleration is zero, and calculating velocity when acceleration is not constant. We will also delve into advanced concepts such as finding velocity with acceleration and displacement, distance, position, height, and radius. Let’s get started!

How to Calculate Velocity with Given Acceleration

Calculating Velocity with Acceleration and Time

When you know the acceleration of an object and the time for which it has been accelerating, you can calculate its velocity using the following formula:

$v = u + at$

Where:
– $v$ represents the final velocity
– $u$ represents the initial velocity
– $a$ represents the acceleration
– $t$ represents the time

To better understand this concept, let’s consider an example:

Example:
A car accelerates from rest with an acceleration of $2 , text{m/s}^2$ for a duration of $5 , text{s}$ . What is its final velocity?

First, we can denote the initial velocity as $u = 0 , text{m/s}$ since the car starts from rest. Using the formula mentioned above, we can calculate the final velocity:

$v = 0 + (2 , text{m/s}^2)(5 , text{s}) = 10 , text{m/s}$

Therefore, the car’s final velocity is $10 , text{m/s}$ .

Finding Velocity with Acceleration and Initial Velocity

In some cases, you may already know the initial velocity of an object along with its acceleration. To find the final velocity, you can use the following formula:

$v = u + at$

This formula is similar to the one mentioned earlier, but here the initial velocity is considered. Let’s take a look at an example to grasp this concept better:

Example:
A ball is thrown vertically upward with an initial velocity of $20 , text{m/s}$ . The acceleration due to gravity is $9.8 , text{m/s}^2$ . What is the ball’s final velocity when it reaches its maximum height?

In this case, we know the initial velocity $(u = 20 , text{m/s}$ ) and the acceleration $(a = -9.8 , text{m/s}^2$ since the ball is moving against gravity). We also know that the time it takes to reach the maximum height is unknown. However, at the maximum height, the ball comes to rest momentarily, which means the final velocity $(v$ ) is $0 , text{m/s}$ . Using the formula mentioned above, we can find the time it takes for the ball to reach the maximum height:

$0 = 20 , text{m/s} - (9.8 , text{m/s}^2)t$

Solving for $t$ , we find:

$t = frac{20 , text{m/s}}{9.8 , text{m/s}^2} approx 2.04 , text{s}$

Therefore, it takes approximately $2.04 , text{s}$ for the ball to reach its maximum height. The final velocity at the maximum height is $0 , text{m/s}$ .

Determining Velocity when Acceleration is Zero

When the acceleration of an object is zero, its velocity remains constant. This means that the object is either at rest or moving at a constant speed. In such cases, the final velocity $(v$ ) is equal to the initial velocity $(u$ ).

Let’s consider an example:

Example:
A car is moving at a constant speed of $30 , text{m/s}$ . What is its final velocity after $10 , text{s}$ ?

Since the car is moving at a constant speed, its acceleration is zero $(a = 0 , text{m/s}^2$ ). Therefore, the final velocity $(v$ ) is equal to the initial velocity $(u$ ):

$v = u = 30 , text{m/s}$

Hence, the car’s final velocity after $10 , text{s}$ is $30 , text{m/s}$ .

Calculating Velocity when Acceleration is Not Constant

In situations where acceleration is not constant, finding velocity requires integration or the use of more advanced techniques. However, in this blog post, we will not be going into the details of those methods. Instead, we will focus on the concept of constant acceleration, which simplifies the calculations.

Advanced Concepts in Finding Velocity with Acceleration

Finding Velocity with Acceleration and Displacement

When you know the initial velocity $(u$ ), acceleration $(a$ ), and displacement $(s$ ) of an object, you can find its final velocity $(v$ ) using the following formula:

$v^2 = u^2 + 2as$

Let’s consider an example to illustrate this concept:

Example:
A rocket traveling at $100 , text{m/s}$ undergoes an acceleration of $10 , text{m/s}^2$ over a distance of $500 , text{m}$ . What is the rocket’s final velocity?

Here, we know the initial velocity $(u = 100 , text{m/s}$ ), the acceleration $(a = 10 , text{m/s}^2$ ), and the displacement $(s = 500 , text{m}$ ). Using the formula mentioned above, we can calculate the final velocity $(v$ ):

$v^2 = (100 , text{m/s})^2 + 2(10 , text{m/s}^2)(500 , text{m})$

Simplifying the equation, we find:

$v^2 = 10000 , text{m}^2/text{s}^2 + 10000 , text{m}^2/text{s}^2$

$v^2 = 20000 , text{m}^2/text{s}^2$

Taking the square root of both sides, we get:

$v = sqrt{20000} , text{m/s} approx 141.42 , text{m/s}$

Therefore, the rocket’s final velocity is approximately $141.42 , text{m/s}$ .

Calculating Velocity with Acceleration and Distance

Similar to the previous concept, you can also find the final velocity $(v$ ) of an object by knowing its initial velocity $(u$ ), acceleration $(a$ ), and the distance traveled $(d$ ). The formula to use in this case is:

$v^2 = u^2 + 2ad$

Let’s work through an example to understand this concept better:

Example:
A skateboarder starts with an initial velocity of $5 , text{m/s}$ and accelerates at $2 , text{m/s}^2$ over a distance of $50 , text{m}$ . What is the skateboarder’s final velocity?

Given the initial velocity $(u = 5 , text{m/s}$ ), acceleration $(a = 2 , text{m/s}^2$ ), and distance $(d = 50 , text{m}$ ), we can use the formula to calculate the final velocity $(v$ ):

$v^2 = (5 , text{m/s})^2 + 2(2 , text{m/s}^2)(50 , text{m})$

Simplifying the equation, we get:

$v^2 = 25 , text{m}^2/text{s}^2 + 200 , text{m}^2/text{s}^2$

$v^2 = 225 , text{m}^2/text{s}^2$

Taking the square root of both sides, we find:

$v = sqrt{225} , text{m/s} = 15 , text{m/s}$

Hence, the skateboarder’s final velocity is $15 , text{m/s}$ .

Determining Velocity with Acceleration and Position

In certain scenarios, you might know the initial velocity $(u$ ), acceleration $(a$ ), and the position $(x$ ) of an object. To find the final velocity $(v$ ), you can use the following formula:

$v^2 = u^2 + 2ax$

Let’s consider an example to understand this concept better:

Example:
A train starts from rest and accelerates at $2 , text{m/s}^2$ to reach a position $x = 100 , text{m}$ . What is the train’s final velocity?

Here, we know the initial velocity $(u = 0 , text{m/s}$ ), acceleration $(a = 2 , text{m/s}^2$ ), and position $(x = 100 , text{m}$ ). Using the formula mentioned above, we can calculate the final velocity $(v$ ):

$v^2 = (0 , text{m/s})^2 + 2(2 , text{m/s}^2)(100 , text{m})$

Simplifying the equation, we find:

$v^2 = 0 , text{m}^2/text{s}^2 + 400 , text{m}^2/text{s}^2$

$v^2 = 400 , text{m}^2/text{s}^2$

Taking the square root of both sides, we get:

$v = sqrt{400} , text{m/s} = 20 , text{m/s}$

Therefore, the train’s final velocity is $20 , text{m/s}$ .

Calculating Velocity with Acceleration and Height

When dealing with vertical motion, such as objects falling or being thrown vertically, we can find the final velocity $(v$ ) by knowing the initial velocity $(u$ ), acceleration $(a$ ), and the height $(h$ ) of an object. The formula to use in this case is:

$v^2 - u^2 = 2ah$

Let’s work through an example to understand this concept better:

Example:
A ball is thrown vertically upward with an initial velocity of $10 , text{m/s}$ . The acceleration due to gravity is $9.8 , text{m/s}^2$ . What is the ball’s final velocity when it reaches a height of $20 , text{m}$ above the starting point?

Here, we know the initial velocity $(u = 10 , text{m/s}$ ), the acceleration $(a = -9.8 , text{m/s}^2$ since the ball is moving against gravity), and the height $(h = 20 , text{m}$ ). Using the formula mentioned above, we can calculate the final velocity $(v$ ):

$v^2 - (10 , text{m/s})^2 = 2(-9.8 , text{m/s}^2)(20 , text{m})$

Simplifying the equation, we find:

$v^2 - 100 , text{m}^2/text{s}^2 = -392 , text{m}^2/text{s}^2$

$v^2 = -292 , text{m}^2/text{s}^2 + 100 , text{m}^2/text{s}^2$

$v^2 = -192 , text{m}^2/text{s}^2$

Taking the square root of both sides, we get:

$v = sqrt{-192} , text{m/si}$

Since we cannot take the square root of a negative number in the real number system, this result is not physically meaningful. It indicates that the ball will not reach the specified height with the given initial velocity. Instead, it will fall back down before reaching that point.

Finding Velocity with Acceleration and Radius

When an object moves in a circular path with constant acceleration towards the center, such as in uniform circular motion, you can use the following formula to find its final velocity $(v$ ):

$v = sqrt{u^2 + 2ar}$

Where:
– $v$ represents the final velocity
– $u$ represents the initial velocity
– $a$ represents the acceleration
– $r$ represents the radius of the circular path

Let’s consider an example to illustrate this concept:

Example:
A car is moving along a circular track with a radius of $10 , text{m}$ . Its initial velocity is $5 , text{m/s}$ , and the acceleration towards the center is $2 , text{m/s}^2$ . What is the car’s final velocity?

Given the initial velocity $(u = 5 , text{m/s}$ ), the acceleration towards the center $(a = 2 , text{m/s}^2$ ), and the radius of the circular track $(r = 10 , text{m}$ ), we can use the formula mentioned above to calculate the final velocity $(v$ ):

$v = sqrt{(5 , text{m/s})^2 + 2(2 , text{m/s}^2)(10 , text{m})}$

Simplifying the equation, we find:

$v = sqrt{25 , text{m}^2/text{s}^2 + 40 , text{m}^2/text{s}^2}$

$v = sqrt{65 , text{m}^2/text{s}^2}$

Taking the square root of both sides, we get:

$v = sqrt{65} , text{m/s}$

Hence, the car’s final velocity is $sqrt{65} , text{m/s}$ .

Worked Out Examples

Now that we have explored various methods to find velocity with acceleration, let’s apply these concepts to some practical examples.

Example of Calculating Velocity with Given Acceleration and Time

Example:
A bicycle accelerates from rest with an acceleration of $2 , text{m/s}^2$ for a duration of $3 , text{s}$ . What is its final velocity?

Given:
$u = 0 , text{m/s}$ (initial velocity)
$a = 2 , text{m/s}^2$ (acceleration)
$t = 3 , text{s}$ (time)

To find the final velocity $(v$ ), we can use the formula:

$v = u + at$

Substituting the given values, we get:

$v = 0 + (2 , text{m/s}^2)(3 , text{s}) = 6 , text{m/s}$

Therefore, the bicycle’s final velocity is $6 , text{m/s}$ .

Example of Finding Velocity with Given Acceleration and Initial Velocity

Example:
A car is traveling at an initial velocity of $20 , text{m/s}$ and undergoes an acceleration of $2 , text{m/s}^2$ . What is its final velocity?

Given:
$u = 20 , text{m/s}$ (initial velocity)
$a = 2 , text{m/s}^2$ (acceleration)

To find the final velocity $(v$ ), we can use the formula:

$v = u + at$

However, we are not provided with the time $(t$ ) in this example. Therefore, we cannot directly calculate the final velocity. Additional information is required to solve this problem.

Example of Determining Velocity when Acceleration is Zero

Example:
A race car is moving on a straight track at a constant speed of $100 , text{m/s}$ . What is its final velocity after $10 , text{s}$ ?

Given:
$u = 100 , text{m/s}$ (initial velocity)
$a = 0 , text{m/s}^2$ (acceleration)
$t = 10 , text{s}$ (time)

Since the acceleration is zero $(a = 0 , text{m/s}^2$ ), the final velocity $(v$ ) is equal to the initial velocity $(u$ ). Therefore, the car’s final velocity after $10 , text{s}$ is $100 , text{m/s}$ .

Example of Calculating Velocity when Acceleration is Not Constant

Example:
A rocket is launched into space, and its acceleration changes over time. The acceleration function is given by $a(t) = 40t , text{m/s}^2$ , where $t$ represents time in seconds. If the rocket starts from rest $(u = 0 , text{m/s}$ ), what is its final velocity after $4 , text{s}$ ?

Given:
$u = 0 , text{m/s}$ (initial velocity)
$t = 4 , text{s}$ (time)

Since the acceleration is not constant, we cannot directly use the formula $v = u + at$ to find the final velocity. To determine the final velocity, we would need additional information about how the acceleration changes over time.

Example of Finding Velocity with Given Acceleration and Displacement

Example:
An object slides down a frictionless inclined plane with an acceleration of $3 , text{m/s}^2$ . If it covers a displacement of $50 , text{m}$ along the plane, what is its final velocity?

Given:
$a = 3 , text{m/s}^2$ (acceleration)
$s = 50 , text{m}$ (displacement)

To find the final velocity $(v$ ), we can use the formula:

$v^2 = u^2 + 2as$

However, we are not provided with the initial velocity $(u$ ) in this example. Therefore, we cannot directly calculate the final velocity. Additional information is required to solve this problem.

In this blog post, we explored various methods to find velocity with acceleration. We learned how to calculate velocity with given acceleration and time, find velocity with acceleration and initial velocity, determine velocity when acceleration is zero, and calculate velocity when acceleration is not constant. Additionally, we delved into advanced concepts such as finding velocity with acceleration and displacement, distance, position, height, and radius. By understanding these concepts and applying the appropriate formulas, we can accurately calculate an object’s velocity in different scenarios. Whether you’re solving physics problems or analyzing motion in real-world situations, knowing how to find velocity with acceleration is crucial.

How can the concepts of finding velocity with acceleration and mass be combined?

The combination of acceleration and mass plays a crucial role in calculating velocity. By understanding the relationship between these two variables, one can effectively determine an object’s velocity using the formula Calculating velocity using acceleration and mass. This article explores the intersection of these concepts and provides insights into how velocity can be determined by considering both acceleration and mass. It delves into the mathematical equations and principles involved in this calculation, providing a comprehensive understanding of the topic.

Numerical Problems on How to Find Velocity with Acceleration

Problem 1:

Image by Cdang – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

A car starts from rest and accelerates uniformly at a rate of $3 , text{m/s}^2$ for a duration of $5 , text{s}$ . Find the final velocity of the car.

Solution:

Given:
Initial velocity $(u) = 0 , text{m/s}$ ,
Acceleration $(a) = 3 , text{m/s}^2$ ,
Time $(t) = 5 , text{s}$ .

To find the final velocity $(v)$ , we can use the formula:

$v = u + at$

Substituting the given values, we have:

$v = 0 + 3 times 5$

Simplifying the expression, we get:

$v = 15 , text{m/s}$

Therefore, the final velocity of the car is $15 , text{m/s}$ .

Problem 2:

An object accelerates from a velocity of $4 , text{m/s}$ to a velocity of $12 , text{m/s}$ in a time duration of $6 , text{s}$ . Calculate the acceleration of the object.

Solution:

Given:
Initial velocity $(u) = 4 , text{m/s}$ ,
Final velocity $(v) = 12 , text{m/s}$ ,
Time $(t) = 6 , text{s}$ .

To find the acceleration $(a)$ , we can use the formula:

$a = frac{v - u}{t}$

Substituting the given values, we have:

$a = frac{12 - 4}{6}$

Simplifying the expression, we get:

$a = frac{8}{6} = frac{4}{3} , text{m/s}^2$

Therefore, the acceleration of the object is $frac{4}{3} , text{m/s}^2$ .

Problem 3:

A particle is moving with an initial velocity of $10 , text{m/s}$ and comes to rest after traveling a distance of $80 , text{m}$ with a uniform deceleration. Find the deceleration of the particle.

Solution:

Given:
Initial velocity $(u) = 10 , text{m/s}$ ,
Final velocity $(v) = 0 , text{m/s}$ ,
Distance $(s) = 80 , text{m}$ .

To find the deceleration $(a)$ , we can use the formula:

$v^2 = u^2 - 2as$

Substituting the given values, we have:

$0^2 = 10^2 - 2a times 80$

Simplifying the expression, we get:

$100 = 160a$

Dividing both sides by $160$ , we obtain:

$a = frac{100}{160} = frac{5}{8} , text{m/s}^2$

Therefore, the deceleration of the particle is $frac{5}{8} , text{m/s}^2$ .

Also Read:

How To Find Final Velocity Without Acceleration: Facts, Problems, Examples

January 21, 2024December 30, 2021 by AKSHITA MAPARI

In this article, we are going to discuss how to find final velocity without acceleration along with some examples and facts.

Learn how to calculate an object’s final velocity using its initial speed, energy, position, and the forces acting upon it. Packed with practical examples and fascinating facts, this article is ideal for anyone eager to explore the nuances of physics beyond basic acceleration principles.

Velocity

The velocity is defined as the ratio of displacement of the object upon the time interval given by the relation

Velocity=Displacement/Time

The velocity of the object can be calculated by measuring the total displacement of the object in a specific time interval.

Final velocity

Final velocity comes into the picture when the body has attained the maximum acceleration over a period of time. The acceleration is a difference between the final and the initial velocity of the object during the time.

Based on the motion of the body, whether it is in a planar motion, uniform circular motion, or in a projectile motion, the final velocity attained by the object can be calculated.

Final velocity of an Object in a Linear Motion

The object moving in a plane undergoes various external forces hence the velocity of the object may not be constant every time. The final velocity of the body does depend upon the initial velocity and how much is the velocity varying with time.

Calculate the Final velocity of an Object in a Linear Motion

Let us see the graph of velocity v/s time of the object accelerating in a uniform linear motion with initial velocity â€˜uâ€™ and chasing the final velocity of â€˜vâ€™.

For an object accelerating uniformly, if the initial velocity at time ( t = 0 ) is ( u ), and at a later time ( t ), the velocity increases to ( v ), then the acceleration of the object can be expressed as ( a = v – u ).

To calculate the total area of the plot in the given figure, it is equal to the combined area of the triangle (ΔABC) and the quadrilateral (ACDO).

Since,

v=x/t

x=vt

x = Area(ΔABC) + Area(ACDO)

=1/2 bh+lb

=1/2 t * (v-u)+ut

Since we are interested in finding the velocity without considering the acceleration term which is (v-u)

x=1/2 vt-1/2 ut+ut

x=1/2 vt+1/2 ut

2x=(v+u)t

2x/t=(v+u)

Therefore the final velocity of the object is

v=2x/t-u

On knowing the displacement of the object, the time taken for the displacement, and its initial velocity we can find out the final velocity picked up by the object.

Let us illustrate this with a simple example. Consider a car moving with a velocity of 20km/h starting from point A to reach point B. A car covers a distance of 60kms in 2 hours. What must be the final velocity of the car?

We know the initial velocity of the car u=20km/h,

Duration= 2hrs=120seconds

distance = 60 km

Using the formula derived above

v=2x/t-u=2*60/2-20=60-20=40km/h

Therefore the final velocity of the car will be 40kms/hr.

Projectile motion

An object in a projectile motion will lapse its path in a parabola. The initial and final velocity of the object will differ but the energy is conserved in a process. Initially, when the object is on the ground, it has more potential energy which is converted into kinetic energy for its flight.

Once reaching a particular height where all of its potential energy is transformed into kinetic energy, it falls freely on the ground converting this kinetic energy into potential energy. Hence the energy is conserved in a projectile motion of the object. That is, the sum of the kinetic and potential energy of the object before attaining maximum height is equal to the total energy after a flight.

If ‘u’ is the initial velocity and ‘v’ is the final velocity of an object with mass ‘m’, and ( h_0 ) is the initial height of the object from the ground, while ‘h’ is the highest height attained by the object in the air, then

K.E_initial+P.E_initial=K.E_final+P.E_final

1/2 mu²+mgh₀=1/2 mv²+mgh₁

Solving this equation further,

u²+2gh0=v²+2gh₁

v²=u²+2g(h₀-h₁)

v²=u²-2g(h₁-h₀)

Therefore the final velocity of the object in a projectile motion before it reaches the ground is

v = √(u² – 2g(h₁ – h₀))

The change in the velocity of the object in projectile motion is Δv = v – u.

Ponder upon the helicopter dropping food parcels to people in a flood-affected area. What will be the velocity of the food parcels dropped from the helicopter flying above at the height of 600m?

Of course, the initial velocity of the parcel will be zero before dropping it from the helicopter, i.e. u=0, and the height of the helicopter from above the ground is given h=600m. Let v be the final velocity of the food parcel when it is released from the helicopter.

Substituting in the equation below

v = √(u² – 2g(h₁ – h₀))

v = √(0² – 2 * 10 * (0 – 600))

v = √12000 = 109.54 m/s

Hence, t=600/109.54=5.47 seconds Â is the time required to reach the food parcel to the ground once it is dropped from the helicopter.

Read more on Projectile Motion.

Velocity of the object in a circular motion

An object moving in a circular motion exerts a centrifugal force and centripetal force which are equal and opposite in direction and is given by the relation

F_c=mv²/r

The velocity of the object is always perpendicular to both these forces directing outward from the circular path. Due to which the velocity is the change in displacement with respect to time.

If the initial velocity of an object with mass ‘m’ accelerating on a circular track with radius ‘r’ is ‘u’, and ‘v’ is the final velocity of the object, then the net force acting on the object is

F=F₂+F₂

=mv²/r+mu²/r

=m/r ( v²+u²)

(r/m) F=v²-u²

v²=u²+r/m F

Therefore the final velocity of the object accelerating in a circular path is

v = √(u² + r/m F)

Frequently Asked Questions

Q1.What is the final velocity of the ball accelerating downward on rising at the height of 5m from above the ground, if the mass of the ball is 500 grams? Consider the initial velocity of the ball to be 3m/s.

Given: m=500 grams

h₀=5m

h₁=0

The initial velocity of the ball u=3m/s

Since the motion of the ball is in a projectile motion, the final velocity of the ball is

v = √(u² – 2g(h₁ – h₀))

v = √(3² – 2 * 10 * (0 – 5))

v = √(9 + 100)

v = √109

v=10.44 m/s

It is evident that the speed of the ball accelerating down the ground increases due to the gravitational pull of the Earth on the objects surrounding it.

Q2.If an object moving with its initial velocity of 3 m/s suddenly accelerates and picks up the velocity of 10 m/s. How much distance will the object covers in 5 minutes?

The initial velocity of the object is u=3m/s

The final velocity of the object is v=10m/s

Duration t= 5 minutes= 5* 60=300 seconds

v=2x/t-u

10=2x/300-3

13*300=2x

2x=3900

therefore x=1950 m

x=1.95 km

In a duration of 5 minutes, the object will cover a distance of 1.95 km.

Q3. The distance from Ratan’s house to her school is 800 meters. She begins walking to school from her house at 7:45 AM with an initial velocity of 0.8 m/s. She needs to be at school 5 minutes before 8:00 AM, so she increases her walking speed and arrives on time. What was her final walking speed?

Given: d=800m,

t=10 min = 10*60 =600seconds

Initial walking speed u=0.8 m/s

Hence,

v=2x/t-u

v=2*800/600-0.8

v=8/3-0.8

v=8-2.4/3=5.6/3=1.87 m/s

Hence, the final walking speed of Ratan was 1.87 m/s.

Q4.What will be the velocity of the object of mass 30 kg moving with initial velocity 3m/s which accelerates at a rate of 4m/s on the application of force of 15N?

The final velocity of the object is equal to the sum of the initial velocity and acceleration with time.

Hence, the final velocity of the object is V_initial+V_accelerating= 3m/s+4m/s=7m/s

Also Read:

Difference Between Internal And External Forces: Exhaustive Insights

January 20, 2024December 29, 2021 by AKSHITA MAPARI

In this article, we are going to discuss what is the difference between internal and external forces.

Internal forces are the forces exerted from within the system whereas external forces are the forces imposed on the system from the surrounding.

Difference Between Internal And External Forces

Internal Forces	External Forces
Force experiencing within the system without any external potency is known as internal force.	Force acting on the system from the surroundings due to external agents is called external force.
The center of mass of the system is immovable as there is no momentum of the system.	The Center of gravity of mass varies with time as the system gains momentum due to external forces.
Energy is sustained in the form of mechanical energy.	Mechanical energy is converted into kinetic or potential energy of the system.
Internal force is a conservative force.	The external force is not a conservative force.
The internal forces acting within the system are in opposite directions to each other, the forces cancel out and hence there is no net work done on the system.	The external forces act in the direction of the force imposed and the work is done.
Some examples of internal forces are gravitational force, magnetic force, electric force, spring force, etc.	Examples of external forces are frictional force, applied force, normal force, tension force, air drag, etc.

What is Internal Force?

The internal force reacting within the object doesn’t cause the acceleration of the object at rest but there are internal actions that result in a change of energy of the system.

Internal forces are the forces acting within the system, which may be due to dipole moment, the motion of the molecules or charged particles, density, etc. Examples of internal forces are gravitational force, electric and magnetic forces, spring force, etc.

Due to the internal actions, the potential or kinetic energy of the object changes to the mechanical energy of the object which is conserved by the system. Since the acceleration of the object due to internal forces is zero, this implies that there is no momentum of the object and hence the work done by the system is always zero and the mechanical energy is also conserved. Hence, the internal force is a conservative force.

How internal forces act on the system?

The internal forces within the system act in a direction opposite to one another thus canceling out and resulting in zero output.

The internal forces mainly appear to resist the changes caused by external forces or in response to the external agents that may be due to electric, magnetic field interaction, or temperature change.

When the conductor is subjected to the electric field, the charged particle moves in a helix but does not cause any exterior change on the object, or cause the acceleration of the center of mass. The motion of the charged particle originates the magnetic field production due to the spin of the electric particle.

On introducing the material having magnetic characteristics in a magnetic field, the dipoles get arranged in the direction of the field. The magnetic flux lines traversing internally cause the magnetic spin dipoles to get aligned according to the field.

An object always exerts a force due to the gravity of the Earth that relies upon the mass of the object.

What is the External Force?

The external forces are the forces acting on the system due to external agency.

The external forces cause the object to displace or resist the motion of the accelerating object. Some external forces are applied force, air resistance, tensional force, normal force, frictional force, etc.

The object at rest has zero kinetic energy, when the external force is applied on the object, the potential energy is converted into the kinetic energy that is utilized in accelerating the object until it experiences a force to resist its motion due to which the kinetic energy is again converted into potential energy.

The work is done in the direction of the applied force. If the work done is positive, it implies that the system gains energy in the form of potential energy or kinetic energy, and if there is a loss of energy from the system then the work done is negative.

How external forces act on the system?

According to Newton’s First Law of Motion, “the object will be in a state of rest on in a continuous motion at constant speed unless and until some external force is exerted on the body.”

The external force is required to either accelerate the body or to resist the motion of the object. This could be applied force, normal force due to the weight of the system, a force due to air resistance, or frictional force exerted on the body that resists the motion of the body dragging it backward.

The equal and opposite force reacting on the object in a direction opposite to the normal force due to weight and geometry, and across the length of the object is a tensional force. This force is created across the length of the body when a load is applied to the material.

Examples

Let us discuss some examples to understand the internal and external forces exerted on the objects.

Car Climbing Up the Hill

Consider a car climbing on a hill. T is a tensional force, N is a normal force, the force due to friction and air drag acting backward and force due to gravity is acting towards the ground from the center of gravity.

Difference Between Internal And External Forces — **Car climbing on the hill**

For a car to climb up the steeper hill, more acceleration has to be given to the car. The steeper the slope of the road more you need to provide the acceleration because the internal force due to gravity is pointing backward and also the frictional force and air resistance drag the car down the slope.

The more the force acting backward, the equal force will be required for a car to climb the hill; this will create a tensional force reacting forward that keeps the car accelerating forward.

Man Pushing a Load

Consider a man pushing a load of mass ‘m’, the force due to gravity on the object is ‘mg’. The normal force is against the weight of the load.

When a force is applied to displace the object, a frictional force is applied on the surface of the object simultaneously on rubbing to the ground. The greater the mass of the object more will be the frictional force into action. The friction of the surface depends upon the pattern of the surface, less friction will be produced if the surface is smooth, more the roughness of the surface more will be the frictional force on the object accelerating on the surface.

Contraction and Expansion of Rocks

Contraction and extension of the rock forming the cleavages on the surface of the rocks are due to the thermal agitation and varying weather conditions causing the cleavages and erosion of the rocks.

See the source image — **Fractures on a rock due to contraction and extension, Image Credit: Pixabay**

During the cold weather, the molecular distance constituting the rocks contracts whereas in the hot summers the molecular distance expands which results in the formation of cleavages on the rocks. This is only due to the internal activities going within the composition of the rock due to the absorption and emissivity of sunrays.

Weight Attached on a Pulley

Consider a pulley with masses attached on both the ends of the rope, m₂>m₁. Since the mass m₂ is greater than m1, m₂ will accelerate down. Due to the weight imposed on both ends of the rope, the tensional force will be created across the length of the rope.

The force acting on the mass m₁ is the sum of the external force due to tension in the rope due to the attached mass and internal force due to gravity acting downward and given by the relation,

F₁=T-m₁g

m₁a₁=T-m₁g

Since the acceleration of the mass m₁ is upward in the direction opposite to the force due to gravity, hence it is negative.

The force acting on the mass m₂ is a gravitational force in the direction of the acceleration of the mass and opposite to the tensional force acting across the length of the rope from the pulley.

F₂=m₂g-T

m₂a₂=m₂g-T

On what factors does the internal and external forces depend?

The internal and the external forces in actuality depend upon the intrinsic as well as the extrinsic factors and amount of force imposed on the object.

The internal forces within the system depend upon the dipole moments, internal heat of the system, emissivity, temperature of the system and the surrounding, composition, weight, density, the separation between the molecules constituting the system, motion of the particles in the system, geometry of the system, molecular constituency, covalent bonds between the atoms, number of free particles, etc.

The external forces depend upon the extrinsic properties influenced on the system like how much is a force applied, the normal force due to weight and configuration, the frictional force due to the surface in contact with the object, the air drag, tensional force, etc.

Frequently Asked Questions

What forces act on the object floating on the surface of the water?

The force that causes the object to float on the water is a buoyant force.

The buoyant force is acting upwards on the object due to the volume of water which is the external force, whereas the internal force of the object that is the force due to gravity is always acting downward.

What are the various forces employed on the bullet fired from the rifle?

On firing the bullet, the accelerating force is applied on a bullet equal and opposite to the recoiling force on the gun.

When a bullet is in the air traversing the air column, the air resistance drags the motion of the bullet due to which the frictional force comes into the act as the bullet passes brushing the air while the gravitational force is acting downward.

What forces are associated with the athlete while running?

The athletic is able to run because of the gravitational force acting downward and the frictional force that prevents the athletic from falling.

Most importantly the muscular force is required by the athlete to accelerate his/her body which is an internal force involved by the athlete.

Why the center of gravity of an object doesn’t change on the application of internal forces?

On acceleration of the object the center of mass moves along with it.

The object doesn’t accelerate due to the cause of internal forces hence the center of gravity remains constant.

Why spring force is an internal force?

The spring force helps the spring to regain its original form. Every spring has different spring constants.

When a load is imposed on the spring it is stretched gaining the potential energy that converts into kinetic energy while the spring tries to come back to its original shape and size resulting in harmonic oscillations.

Also Read:

Super Elastic Collision: Detailed Facts And FAQs

January 20, 2024December 26, 2021 by AKSHITA MAPARI

Let us discuss some detailed facts about a super elastic collision, how and where does it occurs, some examples, and detailed facts.

Super elastic collisions are those in which the colliding particle does not lose its kinetic energy, instead gains some kinetic energy from the particle it is colliding with and accelerates at a faster rate after the collision.

What is a super elastic collision

The collision is said to be elastic when the momentum and the kinetic energy of the object after the collision are conserved. There may be loss or gain of energy during the collision of the objects.

A collision in which there is no loss of energy instead the object gains an additional amount of energy then the collision is said to be a super elastic collision. This auxiliary supply of kinetic energy may be the result of the conversion of the potential energy of the object into kinetic energy.

Where does super elastic collision occur

Most of the collisions in nature are inelastic collisions where the kinetic energy of the colliding object is converted into some other form of energy.

Well, a super elastic collision occurs mostly in explosive reactions like nuclear fissions, reactors, supernovas, explosions, etc that create critical impact. This is a result due to a gain of the additional amount of kinetic energy without any loss of energy. On collision, subsequently, an object receives the energy from the object it is colliding with, which excels the kinetic energy of the object.

Super elastic collision formula

Consider two molecules of mass m₁ and m₂. A molecule of mass m₁ is approaching from infinity with velocity u₁ and collides with mass m₂ moving at velocity u₂. After a collision, both the masses diverts away from each other making an angle with a plane with velocities v₁ and v₂.

In an elastic collision, the momentum of the particles before and after a collision is conserved, hence given by the relation

m₁u₁+m₂u₂=m₁v₁+m₂v₂

Where m₁, m₂ are masses of particle 1 & 2 respectively

u₁, u₂ are initial velocities of both the particle before colliding, and

v₁, v₂ are final velocities of the particles after collision.

The momentum of the colliding molecule after a collision will be greater than the momentum of the molecule before the collision.

m₁u₁<m₁v₁

Which implies that u₁<v₁

And the kinetic energy of the particle in the collision is

1/2 m₁u₁²+1/2 m₂u₂²=1/2 m₁v₁²+1/2 m₂v₂²

Since u₁<v₁, the kinetic energy of the colliding molecule after colliding will be increased.

1/2 m₁u₁²<1/2 m₁v₁²

This means the energy associated with molecule 2 will be reduced as it will transfer its potential energy to molecule 1 that will convert into kinetic energy.

Super elastic collision example

Let us discuss some examples of super elastic collision to understand the term better.

Nuclear fission

Fission is the process of splitting a reactant into two or more products. A nucleus of the atom splits into two or more nuclei when a highly energetic photon collides with the nuclei.

super elastic collision — **Nuclear Fission**

A photon approaching from infinity carries kinetic energy with it, on bombarding with the nucleus it releases its energy to the nucleus due to which the nucleus becomes unstable. This results in a splitting of the nucleus into two daughter nuclei releasing out the photon.

The mass of the nucleus reduces to half and the potential energy of the nucleus is converted into kinetic energy and hence the final kinetic energy given out in a process after the collision is high. This technique is used in nuclear weapons, in nuclear reactors to produce huge energy.

Shape memory alloys

The shape memory alloys are super elastic materials manufactured at a specific temperature. The alloy is molded into a particular shape while heating, maintaining a certain temperature, and quickly cooling it down. This shape is memorized by the alloy.

An object changes its shape when an external load is imposed on it but regains its shape once the load is removed and exposed to the same temperature at which it was formed. This superelasticity is a reversible process.

Mostly, Copper-Aluminium-Nickel and Nickel-Titanium alloys are used as a shape memory alloy. Nickel-titanium is one such shape memory alloy used in manufacturing orthodontic wires.

Uranium bomb

Uranium-235 is a highly radioactive atom and gives out a large amount of energy during its fission, that is why it is mostly used in reactors and explosives.

This is similar to nuclear fission, the neutron when collides with the uranium-235 atom, the kinetic energy of the neutron is transferred onto a uranium atom and becomes unstable due to an extra neutron availability. This neutron recoils along with the atom.

The highly unstable atom splits up into two daughter nuclei shown in the above diagram, releasing three free nuclei which then react with another atom of uranium for fission. This reaction gives out an enormous amount of energy and heat in the surrounding, thus it is an exothermic reaction.

Spring

The spring when compressed, stores the potential energy in it. On releasing the pressure from the string, it gives out a large amount of potential energy in the form of kinetic energy.

Read more on spring potential energy.

Comet approaching sun

The sun has the highest gravitational attraction force in a solar nebula and hence most of the comets approaching from the far nebula reach around the Sun. They gain enough potential energy through radiations emitted by the Sun and deflect in a parabolic pathway. The kinetic energy of the comet after deflection is far greater than its kinetic energy while approaching the Sun.

Is impulse conserved in an elastic collision

Impulse is defined as a force stimulated on the object in a definite time interval and given by the formula

I=FΔ t

Where I is the impulse

F is a force

Δ t is a change in time.

Impulse is also equal to the change in the momentum of the object.

I=ΔP

Hence, ΔP=F Δ t

In an elastic collision, the change in momentum of the object is equal to the difference between the momentum of the object before and after the collision.

ΔP=m[V_f-V_i]

Where m is a mass of the colliding object.

V_f is the final velocity of the object

V_i is the initial velocity of the object

Therefore,

F Δ t= m[V_f-V_i]

The impulse on the object in a collision can be found out by finding the difference between the velocities of the object before and after colliding.

It is obvious that there is an impulse on the collision on both the objects, but due to the opposite force of reaction the impulse is reduced and canceled out. In most cases, there is a slight change in the momentum of the object.

How do you solve a perfectly elastic collision

In a perfectly elastic collision, there is no loss of the kinetic energy of the object after the collision. The momentum and the kinetic energy of the object in a perfectly elastic collision are conserved.

Consider a particle of mass m₁ accelerating at a velocity u₁ strikes the particle of mass m₂ moving with velocity u₂, then the momentum of particle 1 is m₁ u₁ and that of particle 2 is m₂u₂. Particle 1 approaches particle 2 and collides with it creating a net impact zero and both particles 1 & 2 gains velocity v₁ and v₂ respectively and divert in two different directions.

Since the momentum of the particles is conserved before and after collision

m₁u₁+m₂u₂= m₁v₁+ m₂v₂

There is no loss of kinetic energies of the particles, hence the kinetic energy before and after collision remains unchanged.

1/2 m₁u₁+1/2 m₂u₂=1/2 m₁v₁+1/2 m₂v₂

m₁(u₁-v₁)=m₂(v₂-u₂)

m1/m2=v₂-u₂/u₁-v₁

Frequently Asked Questions

Q1. An object A of mass 5 kg collides with object B at rest at a speed of 3m/s. After colliding both the objects move at a speed of 0.8m/s. What is the mass of object B? What is the impulse on the object due to collision?

Given:m₁=5kg

m₂=?

u₁=3m/s

u₂=0

v₁=v₂=0.8m/s

Since, the momentum is conserved in the collision

m₁u₁+m₂u₂=m₁v₁+m₂v₂

5* 3+m₂*0=5*0.8+m₂*0.8

15+0=4+m₂*0.8

11=m₂*0.8

m₂=11/0.8=13.75kg

The mass of object 2 is 13.75 kg.

The total momentum of the object before the collision is

P_initial=m₁u₁+m₂u₂=5*3+13.75*0=15

P_final=m₁v₁+m₂v₂ = 5*0.8 + 13.75 * 0.8 = 4+11 = 15

The impulse on the object due to collision is

I = ΔP = P_final – P_initial = 15-15 = 0

Hence, there is no impulse conserved in the collision.

What is the impulse due to collision?

An impulse is the duration of the force applied on the particles while colliding.

It is also defined as the change in momentum of the objects before and after a collision and is equal to the force imposed by the object for finite time duration.

How does the impulse defer in a perfectly elastic collision and super elastic collision?

The momentum of the object is conserved hence the impulse becomes zero in a perfectly elastic collision.

In super elastic collision, the momentum of the object increases after colliding as the kinetic energy excels, therefore the impulse is positive.

Also Read:

Is momentum conserved in an elastic collision