Physics

27 Buoyancy Examples: Neutral,Negative,Buoyant Force Example

by
Buoyancy Examples: Neutral,Negative,Buoyant Force Example

Buoyancy is exemplified by submarines, which adjust buoyancy to dive or surface, floating icebergs displacing water equal to their weight, and hot air balloons rising due to lower density than surrounding air. Archimedes’ principle quantifies buoyancy, stating that the upward buoyant force equals the weight of the fluid displaced by the submerged part of the object.

Floating a ball on water

A ball floats on water because of buoyancy. The density of water is more than the ball, so it floats on the water.

Floating a ball on water

Helium gas balloon

Helium is lighter gas whose density is much smaller than the air, so it sails in the air easily. The sailing is due to the buoyancy of the balloon on air medium.

Helium gas balloon

Egg floating

The egg has a special buoyancy character; it always sinks in fresh water and floats on saltwater; this is due to the differences in the density of water and saltwater.

Sailing of boat or ship

Ships and boats sail on the water due to buoyancy. The buoyancy exerted on the ships and boat makes them sail efficiently.

Submarines

Submarines are underwater vehicle that floats due to buoyancy.

Sea, Submarine, Boat, buoyancy examples
Submarine as buoyancy examples
Image credits: Pixabay

Steel object on the water

The steel objects sink into the object because steel is denser than the water. The sink is due to less buoyancy of steel in water.

Duck toy in the bathtub

The duck toys float on the water in the bathtub due to buoyancy.

Bathtub, Splash Around, Ducks, Pleasure, Friends, Happy
Floating of bathtub ducks as buoyancy examples
Image credits: Pixabay

Oil spills

Oil spills float on the water because of the buoyancy exerted on the oil spills.

Floating of rubber

Some rubber objects float on the water because of the buoyancy exerted on them.

Aircraft

The lift and the drag acting on the aircraft while moving in the air are due to the buoyancy.

Fired bullet in the air

When the bullet is fired, it travels in the air. The buoyancy exerted on the bullet makes them move in the air.

Fishes

The fish can swim easily on the water due to buoyancy. The thick swim bladder is expanded and displaces the water, and thus, greater buoyancy is exerted.

A swimmer

A swimmer experiences more buoyancy while swimming. It makes them float on the water easily.

Wooden log floating

Wooden logs are the best buoyancy examples. The float of wooden logs on the water is due to buoyancy.

Paper piece

Paper pieces experience buoyancy at different stages. Initially, it floats on the water; as it absorbs water, it begins to sink. Both are due to buoyancy.

Iceberg floating on water

The icebergs are nothing but the solid form of water. But the density of the solid form is less than the liquid form; hence they float on the water with maximum buoyancy.

Clouds

The floatation of clouds in the sky is due to buoyancy acting on them. The latent releases during the formation of clouds, and the temperature falls, making the air rise. Thus floatation of clouds is additionally enhanced by the buoyancy.

Aquatic plants

Aquatic plants experience a maximum amount of buoyancy which counteracts their weight. The buoyancy developed is responsible for their cells to flexible and soft.

Life jackets

The life jackets provided while swimming and water surfing have the buoyancy to make the user float properly on the water.

Water decorative items

Some of the items used for decoration on the water are of little less dense than the water; thus, they have the buoyancy to float on the water.

Plastic bottles

An empty plastic bottle can float on the water because its average density is less than the water.

Aluminum foils

The buoyancy acting on the aluminum foil depends on its density. A foil with less density than water can float, and the foil with more density sinks in the water.

Hydrometers

A hydrometer is an instrument that is used to measure the density of a liquid. It is one of the best buoyancy examples because it measures the density by the ability of the liquid to achieve buoyancy.

image 66
Floating of Hydrometer
Image credits: Flickr

Leaves

Some of the leaves float on water as well as in the air, and some type of leaves sinks in water after they fall from the tree. The floatation and sink of the leaves depend on the buoyancy.

Sky lanterns

The pressure created when the sky lanterns are ignited, the lanterns rise in the air, and buoyancy helps to keep them sailing in the sky.

Underwater divers

Underwater divers experience the maximum amount of buoyancy to swim in the deep ocean and river.

Skydivers

When a diver dives into the air, he experiences a change in the buoyancy for every second as he is near to achieving the terminal velocity.

Saltwater

Comparing the freshwater with saltwater, saltwater has maximum buoyancy to make the object float. This is because when the salt is added to the water, the density of the water increases.

Neutral buoyancy examples

Neutral buoyancy occurs only when the object’s density is balanced by the medium density, and thus sub immersed situation of the object occurs. In this section, such neutral buoyancy examples are listed.

Scuba divers

A scuba diver has neutral buoyancy. When the diver dives into the sea, he is balanced by gravity, which makes him neither sink nor rise.

Diving, Diver, Scuba Diving, Fins, Blue, Sea, Water
Scuba Diver
Image credits: Pixabay

A fish

A fish is a very good way to explain the neutral buoyancy examples as they are provided with a pair of swing bladders which is operated by balancing the air that makes the fish not sink or rise.

Human body fluid

The human can efficiently swim in the water because of his body fluid and tissues as they are neutral buoyancy in nature.

Hot air balloons

As soon as the hot air balloons are rise in the air, they keep on sailing at a constant rate until they balanced by the air density because they are under neutral buoyancy.

Hot Air Balloon, Captive Balloon, Ride, Balloon
Sailing of Hot air balloons as neutral buoyancy examples
Image credits: Pixabay

Hardwoods

Some of the hardwoods are not completely sinking in water; not they float on the water, but they remain in the submerged state, which is nothing but neutral buoyancy.

Submarines

Submarines are excellent neutral buoyancy examples because they are made to travel in the mid-way of the sea, neither sinking nor rising.

The egg floating on saltwater

When you drop the egg into the saltwater, it will remain in sub immersed state because the density of the egg is balanced by the salt water, causing then not to sink.

Bullets

When the bullets are fired in the air, they will hit the target, falling or rising in the air.

Plastic containers

Some of the plastic containers, when they are subjected to floating on water, will be in the submerged condition due to the balance of density between the container and water.

Hollow steel ball

Even though steel is denser than water and sinks in them, they are balanced by the neutral buoyancy when the steel is of hallow because hollow steel allows the air to balance the density of water to achieve neutral buoyancy.

Watermelon

Watermelon consists of a large amount of water content in it, so when they are immersed in the water, their density will be somewhat equal, and hence watermelon is partially neutral buoyancy in water.

Balloons in water

When the balloon is immersed in water with a plastic material tied to it, the density of the balloon together with the plastic is balanced by the water density to enhance neutral buoyancy.

Rubber bands immersed in water

Suppose a rubber band is immersed in water; initially, they sink, but after some time, they are balanced by the air molecule and rise in the middle, causing them to float.

Toothpicks with plastic material

The toothpicks with plastic material made to immerse in the water, both their densities together become equal to water density, and hence they will float in the water with neutral buoyancy.

Underwater robots

The underwater robots are the remote-controlled robots used for research purposes. They are designed to achieve neutral buoyancy when they fall in the water.

Submerged flexible piping

The submerged flexible pipelines are made up of rubber or plastic, which is enhanced by neutral buoyancy, which accomplishes the self-controlling flexible arrangements.

Lemons

When they drop into the saltwater, Lemons neither try to sink nor try to rise, causing neutral buoyancy.

Human body

The human body with floating materials attains neutral buoyancy. A person without any knowledge of swimming can float, neither sinking nor rising in the water with the floating material.

Soap bubbles in the air

Soup bubbles in the air have neutral buoyancy as they are very light, and density is much equal to air density. They cannot rise in the air as they are very short-lived.

Astronaut’s training

The astronauts are trained by creating the microgravity environment, which traces the neutral buoyancy condition by floating above the surface.

Negative buoyancy examples

Any objects that sink in a fluid medium are referred to as negative buoyancy examples. A list of negative buoyancy examples is given in this section.

A brick in water

A brick can completely sink in the water because its density is much heavier than the water, thus creating negative buoyancy.

Pebbles

When the pebbles are dropped in water, they sink immediately, having a density more than the water.

Spheres dropped in water.

Spheres of iron or steel are much heavier, and they cannot sustain to float on the water, causing them to sink.

Coins in water

The coins sink as soon as you drop them into the water as their density is heavier than the water, so coins in water are negative buoyancy examples.

Diving submarines

When the submarines are about to immerse in the water, they are negatively buoyant. This is because if they do not have negative buoyancy, it is impossible for them to move under the water.

Keys

The keys are negatively buoyant because they sink in the water when you drop them in the water.

Eggs in freshwater

Eggs do not float on the freshwater; they immediately sink as soon as they drop inside the water.

Lemmon in freshwater

Same as eggs, lemons also sink in the freshwater because the density of the lemon is much greater than the water.

Paper clips

Clips used to hold the paper on the board are negative buoyancy as they sink in the water.

Sand

The sand particles are negative buoyancy as they do not Float in the water but sink. So it is the reason behind the sand settling under the water resources.

Bones and muscles

Bones are muscles of a person are negatively buoyancy examples because they are much denser and they are the reason for a man to sink if he does not know swimming.

Shot put

A shot put is much heavier and also denser than the water and air. So they do not fly or float.

Steel tanks

Steel tanks sink in water because of their density. So they have negative buoyancy in water.

Iron screws

Iron screws appear to be light, but their density is more than the water, so they sink and have negative buoyancy in water.

Rice grains in water

If you observe the rice grain, you will get to know it has negative buoyancy. Because when you put rice grains in water, they sink.

Plastic bottles filled with stones

Plastics have very good buoyancy to float on the water, but if you fill the plastic bottle with some stones, it immediately sinks because of stones.

Fishing nets

To catch the fish from the sea or river, one has to throw the net. These nets are negative buoyancy and sink immediately as soon as they throw in the water.

Anchors sink on the ocean floor.

The anchors of the ships and boats are negatively buoyancy as they sink in the ocean. They are one of the reasons for the safe sailing of ships and boats.

Anchor on ocean floor | Ted | Flickr
Anchors Sink in ocean
Image credits: Flickr

Buoyant force examples

The buoyant force is an upward force exerted on the object following the famous Archimedes principle. This section provides a detailed explanation of buoyant force examples.

Submarines

The submarines are able to sail under the sea because of the buoyant force. The buoyant force is balanced by the upward thrust and is able to maintain the floatation of the submarines.

Sailing of parachutes

The upward thrust, lift, and drag are balanced by the buoyant force of the parachutes and help to sail in the air.

Clouds

The floatation and generation of cloud are due to the buoyant force applied to the clouds carried by the wind.

Clouds, Sky, Atmosphere, Blue Sky, Cloudscape
Floating of clouds Image credits: Pixabay

Balloons

The rise and fall of the balloon in the air depends on the buoyant force acting on them.

Hairpins

When the hairpins are dropped in the water, they sink. The buoyant force between the hairpin and water is less and causes sinking. Sinking is also due to the buoyant force.

Iron ball

The heavier iron ball sinks into the water. The ball has neutral buoyancy, and hence buoyant force acting between them cannot balance the upward thrust, so they sink.

Tennis ball

The tennis ball is good at floating on the water. The upward thrust and gravity are equally balanced by the buoyant force; thus, they can float.

Cork

The density of the cork is less than the water, so the upward buoyant force makes the cork float on the water.

Sawdust

Saw specks of dust are lighter, and the density is less compared to water. So when they are put on the water, they float because the upward buoyant force acting on the sawdust is more.

Rubber bands

Rubber bands can float over water because of the buoyant force. Because of the density of rubber bands, the upwards thrust will be more and makes them float.

Firearm bullets

Bullets out from the firearm are well balanced by the buoyant force. So they keep on moving in the air medium until they are hit by the target.

Rocks near the ocean

The rocks near the large ocean are a good example of the buoyant force as they do not sink in the water. The buoyant force acting in the upward direction holds the rocks on the surface.

Froth on water

The froth created on the water is assumed to be massless and can float on the water for a while. The upward force on the water pushes the froth to float on the water.

image 67
Water froth as buoyant force example
Image credits: Flickr

Floating wood

When the wood is floating on the water, the buoyant force opposes the wood from sinking and remaining in the partially immersed state.

Person in water

The weight of the person is necessary to exert an upward force to oppose the person from sinking in the water. The buoyant force always acts opposite to the weight of the object. Thus buoyant force makes the person float.

Plastic box

The plastic box of less density experiences the buoyant force in the fluid medium in the opposite direction and makes them float.

Sheet of paper

The sheet of paper can experience a buoyant force when they fall on the water. They float on water if they experience maximum buoyant force.

Air parcel

The air parcels are of the same density as the surrounding air molecule; hence they experience the buoyant force. This buoyant force is neutral, and it does not even rise nor sink.

Sea divers

The sea divers have much knowledge of buoyant force as they experience a maximum buoyant force when they dive. If they go underwater, the buoyant force will be neutral.

Aircraft and rockets

The aircraft and the rockets in the air experience the buoyant force. An aircraft or rocket is balanced by the four forces in the air for their efficient motion; one of them is the buoyant force which keeps them constantly moving in the air without falling.

Also Read:

The Intricate Relationship between Dew Point and Altitude

by
dew point and altitude

Dew point and altitude are intricately linked through the concept of density altitude, which is a crucial parameter in aviation and meteorology. Density altitude is a measure of air density that takes into account temperature and pressure variations with altitude, and it can be significantly affected by the dew point, which is a measure of the amount of moisture in the air.

Understanding Density Altitude

Density altitude is the altitude at which the air density is equal to the air density at a given location, temperature, and pressure. It is calculated by taking the pressure altitude and correcting it for non-standard temperature and humidity conditions. The formula for calculating density altitude is:

Density Altitude = Pressure Altitude + [(288 – 0.00198 × Temperature in °C) / 288] × 1000

This formula shows that density altitude is primarily a function of temperature and pressure, but it can also be influenced by humidity, as represented by the dew point.

The Effect of Dew Point on Density Altitude

dew point and altitude

According to a study by Guinn and Barry (2016), density altitude is a function only of dew-point temperature for a given pressure altitude. They found that the absolute errors between density altitude calculations that incorporate humidity and those that do not are significant, and they created a simple rule of thumb for diagnosing the impact of humidity on density altitude.

The rule of thumb is that the correction (in feet) is simply twenty times the dew-point temperature in Celsius, or colloquially, “double the dew point and add a zero.” This rule of thumb is shown to limit the percent error in density-altitude calculations to within 5% for the range of dew-point temperatures between 5°C to 30°C and elevations below 6,000 feet, compared to over 20% for the same conditions using the dry case alone.

For example, if the dew point is 15°C, the correction to the density altitude would be:

Dew point correction = 20 × 15°C = 300 feet

This correction would then be added to the density altitude calculated using the standard formula.

The Effect of Altitude on Dew Point

The relationship between dew point and altitude is not a simple one, as it can be influenced by various factors, such as temperature, pressure, and humidity. In general, as altitude increases, the dew point tends to decrease due to the lower air pressure and temperature.

However, the rate of decrease in dew point with altitude can vary depending on the specific atmospheric conditions. For example, in humid environments, the dew point may not decrease as rapidly with altitude as in drier environments.

According to a study by the National Oceanic and Atmospheric Administration (NOAA), the dew point at the summit of Mount Washington (elevation 6,288 feet) was found to be consistently lower than the dew point at the base of the mountain, with an average difference of around 5°C.

Practical Applications of Dew Point and Altitude

The relationship between dew point and altitude has important practical applications, particularly in the field of aviation. Pilots need to be aware of the effects of humidity on density altitude, as it can significantly impact aircraft performance and safety.

For example, if an aircraft is taking off from a high-altitude airport with a high dew point, the density altitude may be much higher than the actual altitude, leading to reduced engine power and lift. This can make it more difficult for the aircraft to take off and climb, potentially increasing the risk of accidents.

Similarly, in the case of landing, a high density altitude due to a high dew point can make it more challenging for the aircraft to slow down and stop, as the reduced air density can affect the effectiveness of the brakes and other systems.

Numerical Examples

To illustrate the impact of dew point on density altitude, let’s consider a few numerical examples:

  1. Scenario 1: Pressure Altitude = 5,000 feet, Temperature = 20°C, Dew Point = 10°C
  2. Density Altitude (without dew point correction) = 5,000 feet
  3. Dew point correction = 20 × 10°C = 200 feet

  4. Corrected Density Altitude = 5,000 feet + 200 feet = 5,200 feet

  5. Scenario 2: Pressure Altitude = 8,000 feet, Temperature = 15°C, Dew Point = 5°C

  6. Density Altitude (without dew point correction) = 8,000 feet
  7. Dew point correction = 20 × 5°C = 100 feet

  8. Corrected Density Altitude = 8,000 feet + 100 feet = 8,100 feet

  9. Scenario 3: Pressure Altitude = 3,000 feet, Temperature = 25°C, Dew Point = 20°C

  10. Density Altitude (without dew point correction) = 3,000 feet
  11. Dew point correction = 20 × 20°C = 400 feet
  12. Corrected Density Altitude = 3,000 feet + 400 feet = 3,400 feet

These examples demonstrate how the dew point can significantly impact the density altitude, and how the simple rule of thumb can be used to quickly estimate the correction.

Conclusion

In summary, dew point and altitude are closely related through the concept of density altitude, which is a crucial parameter in aviation and meteorology. The dew point can significantly affect the density altitude, and the simple rule of thumb of “double the dew point and add a zero” can be used to quickly estimate the correction. Understanding the relationship between dew point and altitude is essential for pilots, meteorologists, and anyone working in fields where air density and its effects are important.

References

  1. Guinn, T. A., & Barry, R. J. (2016). Quantifying the Effects of Humidity on Density Altitude Calculations for Professional Aviation Education. International Journal of Aviation, Aeronautics, and Aerospace, 3(3), 1-10. doi:10.15394/ijaaa.2016.1124
  2. Vaisala. (2019). What is dew point and how to measure it? Retrieved from https://www.vaisala.com/en/blog/2019-09/what-dew-point-and-how-measure-it
  3. NOAA. (2007). Dewpoint and Humidity Measurements and Trends at the Summit of Mount Washington. Retrieved from https://journals.ametsoc.org/view/journals/clim/20/22/2007jcli1604.1.xml
  4. Aviation Stack Exchange. (2017). Does the dew point affect density altitude? Retrieved from https://aviation.stackexchange.com/questions/45095/does-the-dew-point-affect-density-altitude
  5. Embry-Riddle Aeronautical University. (2016). Quantifying the Effects of Humidity on Density Altitude Calculations. Retrieved from https://commons.erau.edu/ijaaa/vol3/iss3/2/

The Definitive Guide to Dew Point and Saturation Point: A Comprehensive Exploration

by
dew point and saturation point

The dew point and saturation point are fundamental concepts in the study of atmospheric moisture, with far-reaching applications in weather forecasting, industrial processes, and beyond. This comprehensive guide delves into the intricate details of these crucial parameters, equipping you with a deep understanding of their underlying principles, measurement techniques, and practical implications.

Understanding Dew Point

The dew point is the temperature at which air becomes saturated with moisture, leading to the formation of dew or frost. This critical parameter is a direct measure of the amount of water vapor present in the air, and it plays a crucial role in various meteorological and industrial applications.

Defining Dew Point

Dew point is the temperature at which the air becomes saturated with water vapor, meaning that the partial pressure of water vapor in the air equals the equilibrium vapor pressure of water at that temperature. At the dew point, the air can no longer hold any more water vapor, and any further cooling will result in the condensation of water droplets or the formation of frost.

The dew point temperature can be calculated using the following formula:

$T_d = \frac{b \times \ln(e/a)}{a – \ln(e/a)}$

Where:
– $T_d$ is the dew point temperature (in °C)
– $a$ and $b$ are constants that depend on the specific formula used (e.g., Clausius-Clapeyron equation, Goff-Gratch equation, or Magnus formula)
– $e$ is the actual vapor pressure of water in the air (in hPa or mbar)

Measuring Dew Point

Dew point can be measured using various techniques, each with its own advantages and limitations. Some common methods include:

  1. Chilled Mirror Hygrometer: This device cools a mirror until dew or frost forms on its surface, at which point the temperature of the mirror is recorded as the dew point.
  2. Capacitive Sensors: These sensors measure the change in capacitance of a material as it absorbs moisture from the air, allowing for the calculation of the dew point.
  3. Psychrometric Measurements: By measuring the dry-bulb and wet-bulb temperatures of the air, the dew point can be determined using psychrometric charts or equations.

The choice of measurement technique depends on factors such as the required accuracy, the operating environment, and the specific application.

Uncertainty in Dew Point Measurements

Accurate dew point measurements are crucial in many applications, and the uncertainty associated with these measurements has been extensively studied. The National Institute of Standards and Technology (NIST) and the International Organization for Standardization (ISO) have developed guidelines for quantifying the uncertainty of derived dew point temperature and relative humidity.

The uncertainty can be calculated using the law of propagation of uncertainty, also known as the root sum-of-squares (RSS) method. This approach takes into account the uncertainties of the input parameters, such as temperature, pressure, and relative humidity, to derive the combined standard uncertainty of the dew point temperature.

By multiplying the combined standard uncertainty by a coverage factor (typically 2 for a 95% confidence level), the expanded uncertainty of the dew point temperature can be obtained. This information is essential for understanding the reliability and limitations of dew point measurements in various applications.

Saturation Point

dew point and saturation point

The saturation point is the temperature at which the air becomes completely saturated with water vapor, leading to the formation of dew or frost. This point is closely related to the dew point, as it represents the maximum amount of water vapor that the air can hold at a given temperature and pressure.

Defining Saturation Point

The saturation point is the temperature at which the partial pressure of water vapor in the air equals the equilibrium vapor pressure of water at that temperature. At the saturation point, the relative humidity of the air is 100%, and any further increase in water vapor content will result in the condensation of water droplets or the formation of frost.

The saturation point can be calculated using the same formulas used for dew point calculations, such as the Clausius-Clapeyron equation or the Goff-Gratch equation. These equations relate the equilibrium vapor pressure of water to the temperature, allowing for the determination of the saturation point.

Relationship between Dew Point and Saturation Point

The dew point and saturation point are closely related, as they both represent the point at which the air becomes saturated with water vapor. However, there are some key differences:

  1. Definition: The dew point is the temperature at which the air becomes saturated, while the saturation point is the temperature at which the air is completely saturated.
  2. Relative Humidity: At the dew point, the relative humidity is 100%, while at the saturation point, the relative humidity is also 100%.
  3. Condensation: At the dew point, water vapor begins to condense into dew or frost, while at the saturation point, the air is fully saturated, and any further increase in water vapor will result in condensation.

Understanding the relationship between dew point and saturation point is crucial in various applications, such as weather forecasting, HVAC systems, and industrial processes.

Practical Applications of Dew Point and Saturation Point

The dew point and saturation point have numerous practical applications, including:

  1. Weather Forecasting: Dew point is used to predict the likelihood of precipitation, fog, and other weather phenomena.
  2. HVAC Systems: Dew point is monitored to ensure proper humidity control and prevent condensation in buildings and industrial facilities.
  3. Compressed Air Systems: Dew point is a critical parameter in compressed air applications, as it is used to monitor the moisture content and comply with industry standards.
  4. Pharmaceutical and Food Processing: Dew point and saturation point are important in controlling the moisture content and preventing spoilage in these industries.
  5. Material Science: Dew point and saturation point are relevant in the study of phase changes, crystal growth, and other material properties.

By understanding the intricacies of dew point and saturation point, professionals in various fields can optimize their processes, ensure compliance with regulations, and make informed decisions based on accurate data.

Conclusion

The dew point and saturation point are fundamental concepts in the study of atmospheric moisture, with far-reaching applications in weather forecasting, industrial processes, and beyond. This comprehensive guide has explored the definitions, measurement techniques, and practical implications of these crucial parameters, equipping you with the knowledge to navigate the complexities of this field.

Whether you’re a meteorologist, an HVAC engineer, or a material scientist, understanding the nuances of dew point and saturation point is essential for making informed decisions and optimizing your processes. By leveraging the insights and techniques presented in this guide, you can unlock new possibilities and drive innovation in your respective domains.

References:

  1. Vaisala. (2019). What is dew point and how to measure it? Retrieved from https://www.vaisala.com/en/blog/2019-09/what-dew-point-and-how-measure-it
  2. National Digital Forecast Database Definitions. (n.d.). Dew point temperature. Retrieved from https://graphical.weather.gov/supplementalpages/definitions.php
  3. Climate Data Library. (n.d.). How do I calculate dew point? Retrieved from https://iridl.ldeo.columbia.edu/dochelp/QA/Basic/dewpoint.html
  4. Journals of Atmospheric Sciences. (1996). Uncertainties of Derived Dewpoint Temperature and Relative Humidity. Retrieved from https://journals.ametsoc.org/view/journals/apme/43/5/2100.1.xml
  5. Process Sensing. (n.d.). Dew Point Definition and How to Measure It for Industries. Retrieved from https://www.processsensing.com/en-us/blog/dew-point-definition-and-how-to-measure-it-for-industries.htm

The Physics of Dew Point and Fog: A Comprehensive Guide

by
dew point and fog

Dew point and fog are closely related atmospheric phenomena that are characterized by the presence of condensed water vapor in the air. Understanding the physics behind these phenomena is crucial for various applications, from weather forecasting to environmental management. In this comprehensive guide, we will delve into the technical details of dew point and fog, exploring the underlying principles, measurement techniques, and their real-world implications.

Understanding Dew Point

Dew point is the temperature at which the air becomes saturated with water vapor, resulting in the condensation of water droplets. This temperature is determined by the amount of water vapor present in the air, which is typically expressed as relative humidity.

The relationship between dew point and relative humidity can be described by the Clausius-Clapeyron equation, which relates the saturation vapor pressure of water to temperature:

$e_s = e_0 \exp\left(\frac{L_v}{R_v}\left(\frac{1}{T_0} – \frac{1}{T}\right)\right)$

Where:
– $e_s$ is the saturation vapor pressure (Pa)
– $e_0$ is the reference saturation vapor pressure (Pa)
– $L_v$ is the latent heat of vaporization of water (J/kg)
– $R_v$ is the specific gas constant for water vapor (J/kg/K)
– $T_0$ is the reference temperature (K)
– $T$ is the absolute temperature (K)

The dew point temperature can be calculated from the relative humidity and air temperature using the following formula:

$T_d = \frac{b\gamma}{a – \gamma \log(RH)} + 273.15$

Where:
– $T_d$ is the dew point temperature (°C)
– $a = 17.27$
– $b = 237.7$ °C
– $\gamma = \log(RH) + (b/(a + T))$
– $RH$ is the relative humidity (%)
– $T$ is the air temperature (°C)

Measuring dew point is typically done using a sling psychrometer, which consists of two thermometers: one with a dry bulb and one with a wet bulb. The difference in temperature between the two thermometers is used to calculate the dew point.

Fog Formation and Characteristics

dew point and fog

Fog is a visible aerosol of tiny water droplets or ice crystals suspended in the air near the Earth’s surface. Fog formation is closely linked to the dew point, as it occurs when the air temperature drops to the dew point temperature, causing the air to become saturated and leading to the condensation of water droplets or ice crystals.

The formation of fog can be described by the following process:

  1. Cooling of air: As air cools, its capacity to hold water vapor decreases, and the relative humidity increases.
  2. Saturation: When the air temperature reaches the dew point, the air becomes saturated with water vapor, and condensation begins.
  3. Droplet formation: The water vapor condenses on small particles in the air, such as dust, smoke, or other aerosols, forming tiny water droplets or ice crystals.
  4. Fog development: The suspended water droplets or ice crystals scatter and absorb light, making the fog visible.

The characteristics of fog can be quantified using various parameters, such as:

  1. Visibility: Fog reduces visibility by scattering and absorbing light. Visibility is a commonly used parameter for fog and is measured in meters or miles.
  2. Liquid water content (LWC): LWC is the mass of water per unit volume of air and is typically measured in grams per cubic meter (g/m³).
  3. Droplet size distribution: The size and number of droplets in the fog can affect its optical properties and radiative effects. Droplet size distribution is often measured using laser-based instruments.

Fog can have significant impacts on various aspects of the environment and human activities, such as:

  • Visibility and transportation safety
  • Air quality and atmospheric chemistry
  • Plant growth and soil moisture
  • Renewable energy production (e.g., wind and solar)

Understanding the physics and measurement of dew point and fog is crucial for predicting and mitigating their effects on these sectors.

Dew Point and Fog Measurement Techniques

Accurate measurement of dew point and fog is essential for understanding their behavior and impacts. Here are some common techniques used to measure these atmospheric phenomena:

Dew Point Measurement

  1. Sling Psychrometer: As mentioned earlier, a sling psychrometer consists of two thermometers, one with a dry bulb and one with a wet bulb. The difference in temperature between the two thermometers is used to calculate the dew point temperature.

  2. Chilled-Mirror Hygrometer: This instrument uses a chilled mirror to determine the dew point. As the mirror is cooled, the temperature at which dew forms on the mirror is the dew point temperature.

  3. Capacitive Hygrometer: This type of hygrometer measures the change in capacitance of a thin polymer film as it absorbs or desorbs water vapor, which is then used to calculate the dew point.

Fog Measurement

  1. Visibility Sensors: Visibility sensors measure the amount of light scattered and absorbed by the water droplets or ice crystals in the fog, which is directly related to the visibility.

  2. Liquid Water Content (LWC) Sensors: LWC sensors use various techniques, such as optical scattering or hot-wire anemometry, to measure the mass of water per unit volume of air.

  3. Droplet Size Analyzers: These instruments, such as laser-based particle counters, measure the size distribution of the water droplets or ice crystals in the fog.

  4. Nephelometers: Nephelometers measure the scattering of light by the water droplets or ice crystals, which can be used to infer the fog’s optical properties and radiative effects.

The choice of measurement technique depends on the specific application and the desired level of accuracy and resolution. Combining multiple measurement techniques can provide a more comprehensive understanding of dew point and fog characteristics.

Dew Point and Fog in the Real World

Dew point and fog have significant impacts on various aspects of the environment and human activities. Here are some examples of their real-world applications and implications:

Agriculture and Forestry

Dew point and fog can affect plant growth, soil moisture, and the spread of plant diseases. For example, high dew point and fog can lead to increased leaf wetness, which can promote the growth of fungal pathogens. Conversely, low dew point and fog can contribute to plant stress and reduced water availability.

Transportation and Aviation

Fog can significantly reduce visibility, posing a safety hazard for transportation, particularly in areas with complex terrain or high traffic. Accurate dew point and fog forecasting is crucial for airport operations, road safety, and maritime navigation.

Renewable Energy

Dew point and fog can impact the performance of renewable energy systems, such as solar panels and wind turbines. Fog can reduce the amount of solar radiation reaching the panels, while high dew point can affect the efficiency of wind turbines by altering the air density and flow patterns.

Atmospheric Chemistry and Climate

Dew point and fog can influence atmospheric chemistry by affecting the formation and deposition of pollutants, as well as the cycling of water and other essential nutrients. Additionally, changes in dew point and fog patterns can be indicators of broader climate trends and can have implications for climate modeling and adaptation strategies.

Understanding the physics and measurement of dew point and fog is crucial for predicting and mitigating their effects on these and other sectors. By combining advanced measurement techniques, detailed data analysis, and interdisciplinary collaboration, we can better understand and manage the complex interactions between dew point, fog, and the environment.

References

  1. Quantification of Dew and Fog Water Inputs for Swiss Grasslands. Meeting Organizer, Copernicus.org, 2019.
  2. Weather Parameter Definitions. Glen Allen Weather, 2024.
  3. Quantification of Dew and Fog Water Inputs to Swiss Grasslands. ResearchGate, 2018.
  4. Dewpoint and Humidity Measurements and Trends at the Summit of Mauna Loa. Journal of Climate, 2007.
  5. Dewpoint and Cloud Formation. Reddit, 2014.
  6. Lanzante, J. R. (1996). A statistical multiple change-point technique for climate division. Journal of Climate, 9(11), 2758-2775.
  7. Graybeal, J. E., et al. (2004). Quality control of temperature, dew point, and pressure data from the Global Historical Climatology Network. Journal of Atmospheric and Oceanic Technology, 21(10), 1632-1646.
  8. Wright, J. S. (1995). The US standard atmosphere, 1976. National Oceanic and Atmospheric Administration, National Weather Service, Silver Spring, MD.

How to Find the Freezing Point of a Solution

by
how to find freezing point of a solution

The freezing point of a solution is the temperature at which the solution transitions from a liquid state to a solid state. To find the freezing point of a solution, we need to understand the concept of freezing point depression, which is the decrease in the freezing point of a solvent due to the presence of a solute.

Understanding Freezing Point Depression

Freezing point depression is a colligative property, which means that it depends on the concentration of the solute in the solution, but not on the identity of the solute. The formula for calculating the freezing point depression is:

ΔTf = iKfm

Where:
– ΔTf is the freezing point depression (the decrease in freezing point)
– i is the van ‘t Hoff factor, which represents the number of particles formed when the solute dissolves
– Kf is the freezing point depression constant of the solvent
– m is the molality of the solution (moles of solute per kilogram of solvent)

The freezing point depression constant (Kf) is a characteristic of the solvent and can be found in reference tables. For water, the Kf value is 1.86 °C/m.

Calculating the Freezing Point of a Solution

how to find freezing point of a solution

To find the freezing point of a solution, follow these steps:

  1. Determine the molality (m) of the solution.
  2. Molality is the number of moles of solute per kilogram of solvent.

  3. To calculate molality, divide the number of moles of solute by the mass of the solvent in kilograms.

  4. Identify the van ‘t Hoff factor (i) for the solute.

  5. For non-electrolytes, i = 1 (one particle per solute molecule).

  6. For electrolytes, i is the number of ions formed per formula unit of the solute.

  7. Find the freezing point depression constant (Kf) for the solvent.

  8. For water, Kf = 1.86 °C/m.

  9. Calculate the freezing point depression (ΔTf) using the formula:
    ΔTf = iKfm

  10. Subtract the freezing point depression from the freezing point of the pure solvent to find the new freezing point of the solution.

  11. For water, the freezing point is 0.0 °C.
  12. Tf = 0.0 °C – ΔTf

Example Problems

  1. A solution is prepared by dissolving 15.0 g of NaCl in 500.0 g of water. What is the freezing point of the solution?
  2. Molality (m) = (15.0 g NaCl) / (500.0 g H2O) = 0.0300 mol/kg
  3. Van ‘t Hoff factor (i) = 2 (NaCl dissociates into 2 ions)
  4. Kf for water = 1.86 °C/m
  5. ΔTf = (2)(1.86 °C/m)(0.0300 m) = 0.112 °C

  6. Tf = 0.0 °C – 0.112 °C = -0.112 °C

  7. A solution is prepared by dissolving 25.0 g of glucose (C6H12O6) in 100.0 g of water. What is the freezing point of the solution?

  8. Molality (m) = (25.0 g glucose) / (100.0 g H2O) = 0.139 mol/kg
  9. Van ‘t Hoff factor (i) = 1 (glucose is a non-electrolyte)
  10. Kf for water = 1.86 °C/m
  11. ΔTf = (1)(1.86 °C/m)(0.139 m) = 0.258 °C

  12. Tf = 0.0 °C – 0.258 °C = -0.258 °C

  13. A solution is prepared by dissolving 10.0 g of CaCl2 in 250.0 g of water. What is the freezing point of the solution?

  14. Molality (m) = (10.0 g CaCl2) / (250.0 g H2O) = 0.0400 mol/kg
  15. Van ‘t Hoff factor (i) = 3 (CaCl2 dissociates into 3 ions)
  16. Kf for water = 1.86 °C/m
  17. ΔTf = (3)(1.86 °C/m)(0.0400 m) = 0.223 °C
  18. Tf = 0.0 °C – 0.223 °C = -0.223 °C

Additional Considerations

  • The freezing point depression is directly proportional to the molality of the solution and the van ‘t Hoff factor.
  • The freezing point depression constant (Kf) is a characteristic of the solvent and can be found in reference tables.
  • For solutions with multiple solutes, the freezing point depression is the sum of the individual freezing point depressions.
  • Freezing point depression is an important concept in various applications, such as the use of salt to melt ice on roads and the preservation of food through the addition of solutes.

References

  1. Calculating the Freezing Point of a Solution – YouTube: https://www.youtube.com/watch?v=FQKlY6dM35U
  2. Calculation of Molal Freezing Point Depression Constant: https://chemed.chem.purdue.edu/genchem/probsolv/colligative/kf1.3.html
  3. How do you calculate freezing point depression?: https://socratic.org/questions/how-do-you-calculate-freezing-point-depression
  4. Colligative Properties of Solutions – Introductory Chemistry: https://chem.libretexts.org/Courses/College_of_Marin/CHEM_114:_Introductory_Chemistry/13:_Solutions/13.09:_Freezing_Point_Depression_and_Boiling_Point_Elevation-_Making_Water_Freeze_Colder_and_Boil_Hotter
  5. Colligative Properties of Solutions: https://opentextbc.ca/introductorychemistry/chapter/colligative-properties-of-solutions/

The Ultimate Guide to Finding Sliding Friction: A Comprehensive Approach

by
how to find sliding friction

Sliding friction, also known as kinetic friction, is a crucial concept in physics that describes the force that opposes the relative motion between two surfaces in contact. Understanding how to accurately determine sliding friction is essential for various applications, from engineering design to everyday problem-solving. In this comprehensive guide, we will delve into the intricacies of calculating sliding friction, providing you with the necessary tools and techniques to master this fundamental topic.

Understanding the Basics of Sliding Friction

Sliding friction is the force that acts on an object as it slides across a surface. This force is proportional to the normal force, which is the force exerted by the surface on the object perpendicular to the surface. The relationship between sliding friction, normal force, and the coefficient of kinetic friction is expressed by the formula:

fk = μk × N

Where:
– fk is the kinetic (sliding) friction force
– μk is the coefficient of kinetic friction
– N is the normal force

The coefficient of kinetic friction, μk, is a dimensionless quantity that depends on the materials in contact and the surface conditions. It is typically less than the coefficient of static friction, μs, which is the friction force that must be overcome to initiate motion.

Calculating the Normal Force

how to find sliding friction

The normal force, N, is the force exerted by the surface on the object perpendicular to the surface. For an object resting on a flat surface, the normal force is equal to the object’s weight, which can be calculated as:

N = m × g

Where:
– m is the mass of the object
– g is the acceleration due to gravity (9.8 m/s² on Earth)

For example, if an object has a mass of 10 kg and is resting on a flat surface, the normal force would be:

N = 10 kg × 9.8 m/s² = 98 N

Determining the Coefficient of Kinetic Friction

The coefficient of kinetic friction, μk, is a crucial parameter in the calculation of sliding friction. This value depends on the materials in contact and the surface conditions, and it must be determined experimentally or obtained from reference tables.

Here are some typical values of the coefficient of kinetic friction for common material combinations:

Material Combination Coefficient of Kinetic Friction (μk)
Steel on steel 0.10 – 0.15
Aluminum on steel 0.45 – 0.61
Rubber on concrete 0.50 – 0.80
Wood on wood 0.20 – 0.50
Teflon on Teflon 0.04 – 0.10

It’s important to note that the coefficient of kinetic friction can vary depending on factors such as surface roughness, temperature, and the presence of lubricants or contaminants.

Calculating Sliding Friction Force

Once you have determined the normal force and the coefficient of kinetic friction, you can calculate the sliding friction force using the formula:

fk = μk × N

For example, if an object with a mass of 10 kg is resting on a surface with a coefficient of kinetic friction of 0.2, the sliding friction force would be:

fk = 0.2 × (10 kg × 9.8 m/s²) = 19.6 N

Calculating Acceleration with Sliding Friction

When an external force, Fa, is applied to an object on a surface with sliding friction, the total force on the object is the difference between the applied force and the sliding friction force:

F = Fa - fk

Rearranging the equation, we can find the acceleration of the object:

a = (Fa - fk) / m

Where:
– a is the acceleration of the object
– Fa is the applied force
– fk is the sliding friction force
– m is the mass of the object

For example, if an object with a mass of 5 kg is subjected to an applied force of 20 N and the sliding friction force is 10 N, the acceleration of the object would be:

a = (20 N - 10 N) / 5 kg = 2 m/s²

Practical Applications and Examples

Sliding friction is a fundamental concept in physics with numerous practical applications. Here are a few examples:

  1. Braking Systems: Understanding sliding friction is crucial in the design of braking systems for vehicles. The coefficient of kinetic friction between the brake pads and the brake discs or drums determines the braking force and the vehicle’s stopping distance.

  2. Mechanical Devices: Sliding friction plays a crucial role in the design and operation of various mechanical devices, such as bearings, gears, and pulleys. Accurate calculation of sliding friction is necessary to ensure efficient and reliable performance.

  3. Inclined Planes: When an object is placed on an inclined plane, the sliding friction force acts parallel to the surface, opposing the motion of the object. Analyzing the sliding friction force is essential in determining the object’s acceleration or the minimum angle required for the object to start sliding.

  4. Robotics and Automation: In the field of robotics and automation, understanding and controlling sliding friction is crucial for the precise movement and manipulation of objects by robotic systems.

  5. Sports and Recreation: Sliding friction is an important factor in various sports and recreational activities, such as skiing, snowboarding, and ice skating. Analyzing the sliding friction can help athletes and designers optimize equipment and techniques for improved performance.

Conclusion

Mastering the concept of sliding friction is a crucial step in understanding and applying physics principles in various real-world scenarios. By following the comprehensive approach outlined in this guide, you can confidently calculate sliding friction, determine the normal force, and analyze the effects of sliding friction on the motion of objects. This knowledge will empower you to tackle a wide range of physics problems and design more efficient and reliable systems.

References

  1. Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers with Modern Physics (10th ed.). Cengage Learning.
  2. Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics (10th ed.). Wiley.
  3. Hibbeler, R. C. (2018). Engineering Mechanics: Statics (14th ed.). Pearson.
  4. Giancoli, D. C. (2014). Physics for Scientists and Engineers with Modern Physics (4th ed.). Pearson.
  5. Tipler, P. A., & Mosca, G. (2008). Physics for Scientists and Engineers (6th ed.). W. H. Freeman.

How to Find the Coefficient of Static Friction: A Comprehensive Guide

by
how to find coefficient of static friction

The coefficient of static friction, denoted as μs, is a crucial parameter in understanding the behavior of objects in contact with a surface. It represents the ratio of the maximum force of friction that can be exerted before the object starts to slide, to the normal force acting on the object. Knowing the coefficient of static friction is essential in various fields, such as engineering, physics, and everyday life, as it helps predict the stability and movement of objects. In this comprehensive guide, we will delve into the details of how to find the coefficient of static friction using both theoretical and experimental methods.

Understanding the Concept of Static Friction

Static friction is the force that opposes the relative motion between two surfaces in contact with each other when they are at rest. This force arises due to the microscopic irregularities and adhesive forces between the surfaces. The coefficient of static friction, μs, is a dimensionless quantity that represents the ratio of the maximum force of static friction to the normal force acting on the object.

The formula for the coefficient of static friction is:

μs = F/N

Where:
– μs is the coefficient of static friction
– F is the maximum force of static friction
– N is the normal force acting on the object

Theoretical Approach to Finding the Coefficient of Static Friction

how to find coefficient of static friction

  1. Calculating the Normal Force:
  2. The normal force, N, is the force exerted perpendicular to the surface on which the object rests.
  3. For a horizontal surface, the normal force is equal to the weight of the object: N = mg, where m is the mass of the object and g is the acceleration due to gravity.

  4. For an inclined surface, the normal force is the component of the object’s weight perpendicular to the surface: N = mg cos(θ), where θ is the angle of inclination.

  5. Determining the Maximum Force of Static Friction:

  6. The maximum force of static friction, F, is the maximum force that can be applied to the object before it starts to slide.
  7. For a horizontal surface, the maximum force of static friction is the force required to just start the object moving: F = mg sin(θ), where θ is the angle of inclination.

  8. For an inclined surface, the maximum force of static friction is the component of the object’s weight parallel to the surface: F = mg sin(θ).

  9. Calculating the Coefficient of Static Friction:

  10. Once the normal force, N, and the maximum force of static friction, F, are known, the coefficient of static friction can be calculated using the formula: μs = F/N.

Experimental Approach to Finding the Coefficient of Static Friction

  1. Tilting Method:
  2. Place the object on a horizontal surface and gradually tilt the surface until the object just starts to slide.

  3. The angle at which the object starts to slide, θ, is related to the coefficient of static friction by the formula: μs = tan(θ).

  4. Pulling Method:

  5. Place the object on a horizontal surface and attach a force gauge or spring scale to the object.
  6. Gradually increase the force applied to the object until it just starts to slide.
  7. The maximum force of static friction, F, is the force reading on the gauge or scale just before the object starts to slide.
  8. The normal force, N, is the weight of the object: N = mg.

  9. The coefficient of static friction can then be calculated using the formula: μs = F/N.

  10. Inclined Plane Method:

  11. Place the object on an inclined plane and gradually increase the angle of inclination until the object just starts to slide.
  12. The angle at which the object starts to slide, θ, is related to the coefficient of static friction by the formula: μs = tan(θ).
  13. Alternatively, you can fix the angle of the inclined plane and gradually increase the mass of the object until it just starts to slide. The coefficient of static friction can then be calculated using the formula: μs = tan(θ).

Examples and Numerical Problems

  1. Example 1: Box on a Horizontal Surface
  2. A box with a mass of 20 kg is placed on a horizontal surface.
  3. A force of 30 N is applied to the box, and it does not move.
  4. Find the coefficient of static friction between the box and the surface.

Solution:
– Normal force, N = mg = 20 kg × 9.8 m/s^2 = 196 N
– Force of friction, F = 30 N
– Coefficient of static friction, μs = F/N = 30 N / 196 N = 0.153

  1. Example 2: Block on an Inclined Plane
  2. A block with a mass of 5 kg is placed on an inclined plane with an angle of inclination of 30 degrees.
  3. The block does not move.
  4. Find the coefficient of static friction between the block and the plane.

Solution:
– Normal force, N = mg cos(θ) = 5 kg × 9.8 m/s^2 × cos(30°) = 43.3 N
– Force of friction, F = mg sin(θ) = 5 kg × 9.8 m/s^2 × sin(30°) = 24.5 N
– Coefficient of static friction, μs = F/N = 24.5 N / 43.3 N = 0.566

  1. Numerical Problem 1
  2. A 10 kg box is placed on a horizontal surface.
  3. A force of 40 N is required to just start the box moving.
  4. Calculate the coefficient of static friction between the box and the surface.

Solution:
– Normal force, N = mg = 10 kg × 9.8 m/s^2 = 98 N
– Force of friction, F = 40 N
– Coefficient of static friction, μs = F/N = 40 N / 98 N = 0.408

  1. Numerical Problem 2
  2. A 3 kg block is placed on an inclined plane with an angle of 20 degrees.
  3. The block just starts to slide when the angle is increased to 25 degrees.
  4. Calculate the coefficient of static friction between the block and the plane.

Solution:
– Angle at which the block starts to slide, θ = 25 degrees
– Coefficient of static friction, μs = tan(θ) = tan(25°) = 0.466

Factors Affecting the Coefficient of Static Friction

The coefficient of static friction can be influenced by various factors, including:

  1. Surface Roughness: Rougher surfaces generally have a higher coefficient of static friction compared to smoother surfaces.
  2. Surface Materials: The materials of the contacting surfaces can significantly affect the coefficient of static friction. For example, rubber on concrete has a higher coefficient than steel on steel.
  3. Humidity and Temperature: Changes in humidity and temperature can affect the surface properties and, consequently, the coefficient of static friction.
  4. Contamination: The presence of contaminants, such as oil or grease, can reduce the coefficient of static friction between the surfaces.
  5. Surface Coatings: Applying coatings or lubricants to the surfaces can alter the coefficient of static friction.

Practical Applications and Importance

The coefficient of static friction is crucial in various applications, including:

  1. Mechanical Design: Understanding the coefficient of static friction is essential in the design of mechanical systems, such as brakes, clutches, and gears, to ensure proper functioning and safety.
  2. Civil Engineering: The coefficient of static friction is important in the design of structures, such as foundations and retaining walls, to ensure stability and prevent sliding.
  3. Automotive Engineering: The coefficient of static friction between tires and the road surface is crucial for vehicle traction, braking, and handling.
  4. Sports and Recreation: The coefficient of static friction plays a role in the design and performance of sports equipment, such as shoes, skis, and snowboards.
  5. Everyday Life: The coefficient of static friction affects the stability and movement of objects in our daily lives, such as the grip of a shoe on a surface or the ability to push or pull an object.

Conclusion

In this comprehensive guide, we have explored the concept of the coefficient of static friction and the various methods to determine it, both theoretically and experimentally. By understanding the underlying principles and the factors that influence the coefficient of static friction, you can apply this knowledge to a wide range of practical applications, from engineering design to everyday problem-solving. Remember, the key to mastering the concept of the coefficient of static friction lies in a deep understanding of the underlying physics and a thorough practice of the techniques presented in this guide.

References

  1. Coefficient of Static Friction Formula – GeeksforGeeks
    https://www.geeksforgeeks.org/coefficient-of-static-friction-formula/
  2. Measuring the Static Coefficient of Friction – Mini Lab Activity
    https://www.youtube.com/watch?v=gt8mr6pFSFE
  3. Friction Coefficient – an overview | ScienceDirect Topics
    https://www.sciencedirect.com/topics/chemistry/friction-coefficient
  4. Measuring Coefficient of Static Friction – Physics
    http://physics.bu.edu/~duffy/semester1/c6_measuremus.html
  5. L122. Static and Kinetic Friction
    https://a1384-236052.cluster8.canvas-user-content.com/courses/1384~1159/files/1384~236052/course%20files/apb11o/labs/L122/L122_friction.htm

How To Find Co-efficient Of Friction: Detailed Explanations And Problem Examples

by
coefficient of friction 0

When it comes to understanding and analyzing the behavior of objects in contact, the concept of coefficient of friction plays a crucial role. The coefficient of friction is a value that represents the amount of resistance between two surfaces in contact. It helps us understand how objects interact and whether they will slide or remain stationary when a force is applied. In this blog post, we will delve into the details of finding the coefficient of friction, exploring various formulas and methods to determine this important value.

How to Calculate Coefficient of Friction

Coefficient of Friction Formula and its Explanation

The coefficient of friction is determined by dividing the magnitude of the force of friction by the magnitude of the normal force between two objects. It can be calculated using the formula:

\text{Coefficient of Friction} = \frac{F_{\text{friction}}}{F_{\text{normal}}}

where F_{\text{friction}} is the frictional force and F_{\text{normal}} is the normal force.

How to Determine Coefficient of Friction with Acceleration and Mass

In some cases, we can determine the coefficient of friction by considering the acceleration and mass of an object. Let’s say we have an object of mass m moving with an acceleration a . The frictional force acting on this object can be calculated using the formula:

F_{\text{friction}} = m \cdot a

By substituting this value into the coefficient of friction formula, we can find the coefficient of friction.

How to Measure Coefficient of Friction with Mass and Force

Another way to determine the coefficient of friction is by measuring the force required to keep an object in motion. Suppose we have an object of mass m that is being pushed or pulled horizontally with a force F . If we measure this force and calculate the normal force acting on the object, we can find the coefficient of friction using the formula mentioned earlier.

Calculating Coefficient of Friction with Velocity and Distance

In certain situations, we can find the coefficient of friction by considering the velocity and distance traveled by an object. Let’s imagine an object sliding on a surface for a certain distance d with a constant velocity v . By using the equation of motion:

d = v \cdot t

where t is the time taken to travel the distance, we can find the time. Next, we find the acceleration using the formula:

a = \frac{v}{t}

Finally, we can determine the coefficient of friction by substituting the calculated acceleration into the formula mentioned earlier.

Finding Coefficient of Friction with Radius and Velocity

In cases where an object is moving in circular motion, we can calculate the coefficient of friction by considering the radius of the circular path and the velocity of the object. Suppose we have an object moving in a circular path of radius r with a velocity v . The centripetal force required to keep the object moving in the circle can be calculated using the formula:

F_{\text{centripetal}} = m \cdot \frac{v^2}{r}

By substituting this value into the coefficient of friction formula, we can find the coefficient of friction.

Special Cases in Finding Coefficient of Friction

How to Find Coefficient of Friction on an Inclined Plane

When dealing with an inclined plane, the calculation of the coefficient of friction requires considering the angle of inclination. The coefficient of friction can be determined using the formula:

\text{Coefficient of Friction} = \tan(\theta)

where \theta is the angle of inclination.

Determining Coefficient of Friction in Circular Motion

In circular motion, the coefficient of friction can be found by considering the radius, velocity, and mass of the object. By using the same formula mentioned earlier for circular motion, we can calculate the centripetal force and find the coefficient of friction.

Calculating Coefficient of Friction without Normal Force or Mass

In some scenarios, we may not have access to the normal force or mass of an object, making it challenging to directly calculate the coefficient of friction. However, we can still determine the coefficient of friction indirectly by conducting experiments or using data from previous studies.

Experimental Methods to Determine Coefficient of Friction

how to find coefficient of friction
Image by CaoHao – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

How to Conduct an Experiment to Find Coefficient of Friction

To experimentally determine the coefficient of friction, we can follow a simple procedure. First, we need a surface on which the object can slide. We measure the force required to move the object and calculate the normal force. By dividing the measured force by the normal force, we can find the coefficient of friction.

Interpreting the Results of the Experiment

how to find coefficient of friction
Image by Colinvella – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.
coefficient of friction 2

Once the experiment is conducted and the coefficient of friction is calculated, we need to interpret the results. A coefficient of friction less than 1 indicates that the surfaces are relatively smooth, while a value greater than 1 suggests a rougher surface. Understanding the results helps us make informed decisions about materials, surfaces, and their interactions.

By understanding how to find the coefficient of friction and applying the appropriate formulas and methods, we gain valuable insights into the behavior of objects in contact. Whether it’s analyzing the motion of objects on inclined planes, circular paths, or conducting experiments, determining the coefficient of friction allows us to make accurate predictions and design efficient systems that minimize frictional losses.

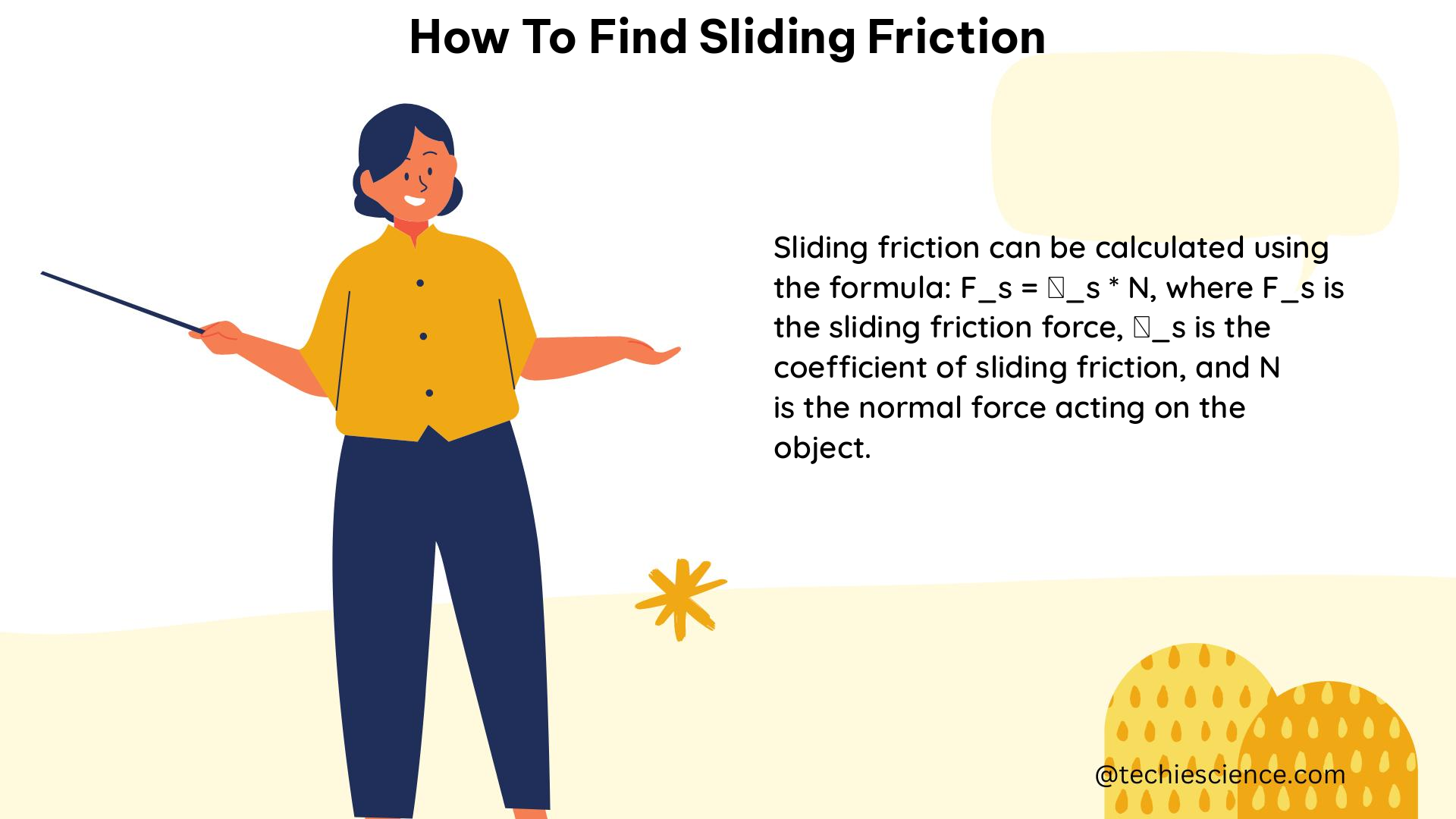
Numerical Problems on how to find coefficient of friction

Problem 1:

A block of mass 5 kg is placed on a horizontal surface. The block is pulled horizontally with a force of 20 N. The block starts moving with an acceleration of 2 m/s^2. Determine the coefficient of friction between the block and the surface.

Solution:

Given:
– Mass of the block, m = 5 kg
– Applied force, F = 20 N
– Acceleration of the block, a = 2 m/s^2

To find the coefficient of friction, we can use the equation:

F - f_{friction} = ma

where f_{friction} is the force of friction.

Since the block is just starting to move, the force of friction can be expressed as:

f_{friction} = \mu_s N

where \mu_s is the coefficient of static friction and N is the normal force. The normal force can be calculated as:

N = mg

where g is the acceleration due to gravity.

Substituting the values into the equation:

20 - \mu_s \cdot 5 \cdot 9.8 = 5 \cdot 2

Simplifying the equation:

20 - 49 \mu_s = 10

Rearranging the equation:

49 \mu_s = 20 - 10

49 \mu_s = 10

\mu_s = \frac{10}{49}

Therefore, the coefficient of static friction is \mu_s = \frac{10}{49} .

Problem 2:

coefficient of friction 1

A box of mass 8 kg is placed on a rough inclined plane. The angle of inclination is 30 degrees. The box starts moving down the plane when a force of 50 N is applied parallel to the plane. Determine the coefficient of kinetic friction between the box and the plane.

Solution:

Given:
– Mass of the box, m = 8 kg
– Applied force, F = 50 N
– Angle of inclination, θ = 30 degrees

To find the coefficient of kinetic friction, we can use the equation:

F - f_{friction} = ma

where f_{friction} is the force of friction.

The force of friction can be expressed as:

f_{friction} = \mu_k N

where \mu_k is the coefficient of kinetic friction.

The normal force can be calculated as:

N = mg \cos \theta

where g is the acceleration due to gravity.

The acceleration of the box down the plane can be calculated as:

a = g \sin \theta

Substituting the values into the equation:

50 - \mu_k \cdot 8 \cdot 9.8 \cdot \cos 30 = 8 \cdot 9.8 \cdot \sin 30

Simplifying the equation:

50 - 78.4 \mu_k = 39.2

Rearranging the equation:

78.4 \mu_k = 50 - 39.2

78.4 \mu_k = 10.8

\mu_k = \frac{10.8}{78.4}

Therefore, the coefficient of kinetic friction is \mu_k = \frac{10.8}{78.4} .

Problem 3:

coefficient of friction 3

A car of mass 1200 kg is moving on a horizontal surface with a velocity of 20 m/s. The car comes to rest after a distance of 100 m. Determine the coefficient of friction between the car tires and the road.

Solution:

Given:
– Mass of the car, m = 1200 kg
– Initial velocity, u = 20 m/s
– Distance, s = 100 m

To find the coefficient of friction, we can use the equation:

v^2 = u^2 + 2as

where v is the final velocity, a is the acceleration, and s is the distance.

Since the car comes to rest, the final velocity is 0.

Substituting the values into the equation:

0 = (20)^2 + 2a \cdot 100

Simplifying the equation:

400 = 200a

Rearranging the equation:

a = \frac{400}{200}

a = 2

The acceleration can be related to the force of friction using the equation:

a = \frac{f_{friction}}{m}

The force of friction can be expressed as:

f_{friction} = \mu N

where \mu is the coefficient of friction and N is the normal force.

The normal force can be calculated as:

N = mg

where g is the acceleration due to gravity.

Substituting the values into the equation:

2 = \frac{\mu \cdot 1200 \cdot 9.8}{1200}

Simplifying the equation:

2 = 9.8 \mu

Rearranging the equation:

\mu = \frac{2}{9.8}

Therefore, the coefficient of friction is \mu = \frac{2}{9.8} .

Also Read:

15 Neutral Equilibrium Examples: Detailed Explanations

by
soccer 488700 960 720

When a body is disturbed from its original equilibrium position, if it tends to remain in its new position, it is said to be in neutral equilibrium.

This post gives you a list of such neutral equilibrium examples.

Detailed Explanation of Neutral equilibrium Examples

In general, the neutral equilibrium can also be stated as “On application of the external force to an object, the system’s equilibrium position is slightly disturbed. Object tends to move to another position, where the system again attains the same equilibrium by achieving a stationary state in the new position without the influence of external force.” In this section, you will learn a detailed explanation of the above-mentioned neutral equilibrium examples.

Motion of sphere

The motion of the sphere on the horizontal surface attains neutral equilibrium when it moves to a new position away from its original position. An external force is required to move the sphere away. When the force is exerted, the sphere begins to move, and after reaching some distance, the sphere retards its motion, and it will remain in its new position without causing further motion. Thus, the motion of the sphere in the horizontal plane is one of the neutral equilibrium examples.

Read more on Unstable equilibrium examples

Ball moving on the ground.

When an external force is applied to the ball, it begins to move, settling in the new position. The ball will remain in its new position until an external force triggers the ball to move. Thus ball acquires the equilibrium in its new position same as the previous position. The ball does not require any external agent to be stationary, so the equilibrium established is nothing but neutral equilibrium.

Soccer, Ball, Stadium, Field, Soccer Stadium, Football
Image Credits: Pixabay

A heavy object dropped to the surface.

Dropping a heavy object from a certain height is one of the excellent neutral equilibrium examples because gravity influences the object to fall and to land on the surface. Due to the heavyweight, the object does not bounce back to its initial position, and it does not undergo further movement, so it will remain in a new position attaining the neutral equilibrium.

Egg-laying on the horizontal surface

The egg-laying on the surface has a neutral equilibrium because of its position. The egg remains in the same position without moving until any external force influences them to move. Even when the egg is made to move by applying force, it will again become stationary as soon as the external force is removed.

Roller

When the roller is disturbed from its previous position and made to move towards another position, the roller will remain in rest at its new position, neither returning to its previous position nor moving further; thus, neutral equilibrium is established.

A car parked on the road without the handbrake

If you park the car on the straight road without the handbrake, the car will be in a stationary state. Thus there is no external force acting on the car to hold it. So the neutral equilibrium comes into play when you park the car without applying the handbrake.

Car, Machine, Auto, Transport, Cars, Parking Lot
Image Credits: Pixabay

Suspension of a charged particle in the sphere

When the charged particle is suspended in the charged sphere, the charged particles never return to their previous position until an external force is exerted. The charged particles remain stationary without the influence of the external source; thus, the charged particle has neutral equilibrium inside the charged sphere.

Sliding a book on the table

To slide the book on the table of a horizontal surface, you exert some force. When you apply some force on the book to slide, it travels some distance and then becomes stationary and never returns to its previous position on its own; thus, neutral equilibrium is established.

Read more on Stable equilibrium examples

Marbles laying on the horizontal surface

Marbles will lay on the horizontal surface without any external force. When an external force acts on the marbles to move them to another position, it will remain in that position and do not move further on its own and never return to its previous position without external force; thus, they have neutral equilibrium.

Pushing a heavy box

If you push a heavy box, it will keep on moving until you keep on pushing. As soon as you stop pushing, the box stops its motion and becomes stationary. If the box is filled with objects, they also become stationary as you stop pushing; thus, neutral equilibrium is established. The box and the object inside the box do not require any external support to hold them stationary.

Support, Help, Pushing, Heavy
Image credits: Pixabay

Pencil on the horizontal surface

The pencil easily rolls on the surface as soon as you touch it because of its shape. When the pencil rolls on the surface, it reaches another position where its motion is retarded. The pencil never returns back to its previous position on its own; thus, neutral equilibrium is set up.

Read more on Thermal equilibrium examples

Applying cream to the skin

Applying cream to the skin is one of the interesting neutral equilibrium examples because viscosity largely influences the cream. Creams such as sunscreen are vicious in nature; thus, the cream will spread over your skin until you spread them over. Viscosity restricts the cream from spreading over on its own. The cream will settle at the position and never movers forward if you stop spreading.

Cream, Lotion, Hands, Sunscreen, Spa, Skin, Wellness
Image Credits: Pixabay

Bottles laying on the horizontal surface

A bottle requires an external force to move, but it does not require any external force to be at rest. The bottle laying on the horizontal surface possesses neutral equilibrium bearing potential energy.

Read more on Static equilibrium examples

Cone resting on its side

Cone resting on one side is balanced by all the forces acting on them as the resultant normal force is acting vertically upward, and the weight of the cone is acting vertically downward. Suppose the position of the cone is slightly displaced; all these forces balance and attain neutral equilibrium.

neutral equilibrium examples
Image of cone as Neutral equilibrium examples

Sliding door

Sliding doors will be in neutral equilibrium before and after sliding. When you slide the door, it overcomes from the stationary state and moves to the other side. As soon as the door reaches the other side, it again acquires a stationary state until you exert some force on them to move.

Floating of a cylindrical log

A cylindrical log has a neutral equilibrium while floating because the log does not move further, and it does not return to its initial position until an external force triggers it.

Floating Logs, Wood In River, Calm Water, Silky Water
Image credits: Pixabay

Read more on Dynamic equilibrium Examples

Also Read: