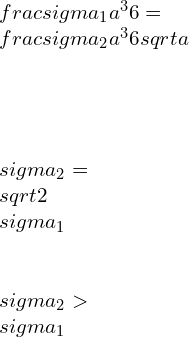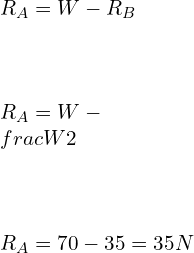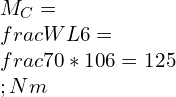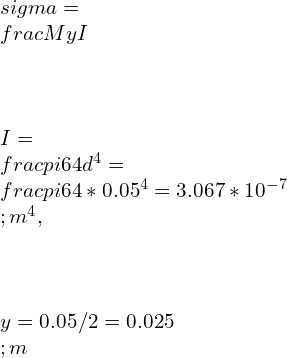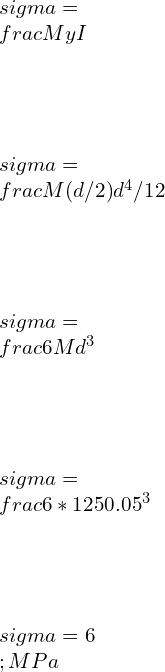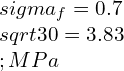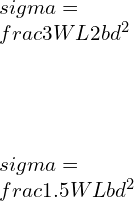What is Hooke’s Law?
Hooke’s law basic properties:
The mechanical behaviour of materials depends on their response to loads, temperature, and the environment. In several practical problems, these controlling parameters’ combined effects must be assessed. However, the individual effects of loads (elastic and plastic deformation) must be studied in detail before attempting to develop an understanding of the combined effects of load and temperature or the effects of load and environment. The material response may also depend on the nature of the loading. When the applied deformation increases continuously with time (as in a tensile test), then reversible (elastic) deformation may occur at small loads before the onset of irreversible/plastic deformation at higher loads. Under reversed loading, the material may also undergo a phenomenon known as ”fatigue.”
Hooke’s Law Definition:
Robert Hooke law 1660. It states that the material’s deformations are directly proportional to the externally applied load on the material.
According to Hooke’s law, the material behavior elastic can be explained as the displacements occurring in the solid material due to some force. The displacement is directly proportional to the force applied.
Does Hooke’s law include proportional limits or elastic limits?
Hooke’s law tell strain of the material is proportionate to the stress applied within the elastic limit of that material.
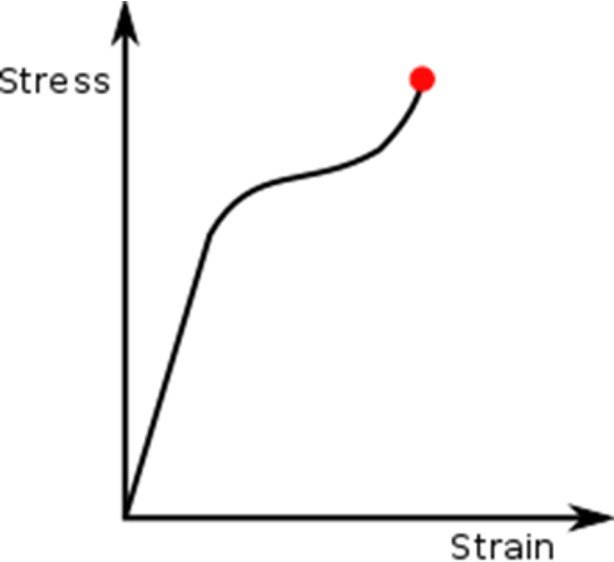
Stress-strain curve for Hooke’s law:
Stress :
The resistance offered by the body against deformation to the applied external force to the unit area is known as stress. The force is applied while stress is induced by the material. A loaded member remains in equilibrium when the externally applied load and the force due to deformation are equal.
![]()
Where,
![]() = Intensity of stress,
= Intensity of stress,
- P= Externally applied load
- A= cross-sectional area
Unit of Stress:
The unit stress depends on the unit of External force and the cross-sectional area.
Force is expressed in Newton, and Area is expressed in m^2.
The unit of stress is N/m^2.
Types of stress:
Tensile stress:
The stress induced in the body due to the stretching of the externally applied load on the material.Results in an increase in the length of the material.
Compressive stress:
The stress induced in the body due to the shortening of the material.
Shear stress:
The stress occurred in the material due to the shearing action of external force.
Strain:
When the body is subjected to external force, there is some change in the dimension of the body.
The strain is represented as the ratio of the change in dimension of the body to that of the original dimension of the body.
![]()
Unit of Strain
The strain is a dimensionless quantity.
Types of strain:
Tensile strain:
The tensile strain is the strain induced due to the change in length.
Volumetric strain:
The volumetric strain is the strain induced due to the change in volume.
Shear strain:
The shear strain is the strain induced due to change in the area of the body.
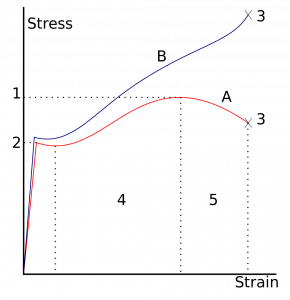
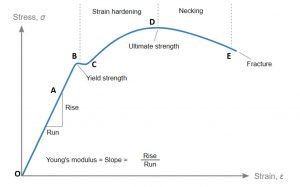
Hooke’s law graph | Hooke’s law experiment graph

Robert Hooke studied springs and the elasticity of the springs and discovered them. The stress-strain curve for various materials has a linear region. Within the proportionality limit, the force applied to pull any elastic object is directly proportional to the displacement of the spring extension.
From the origin to proportionality limit material follows Hook’s Law. Beyond the elastic limit, the material loses its elasticity and behaves like plastic. When the material undergoes elastic limit, After removal of the applied force, the material goes back to its original position.
According to Hookes law stress is directly proportional to strain up to elastic limit but that stress vs strain curve is linear up to proportional limit rather than elastic limit Why ?
Which of these statements is correct All elastic materials follow Hookes law or materials that follow Hookes law are elastic ?
- Answer:
All elastic materials does not follow Hook’s law. There are some elastic materials that does does not obey Hook’s law. so the first statement is invalid. But it is not necessity that materials that follow Hook’s law are elastic, In stress-strain curve for Hook’s law materials follow Hook’s law till their proportional limit and do possess elasticity. Every material has some elastic nature at certain limit and it can store elastic energy at certain point.
What is the difference between Hookes law and Youngs modulus ?
Hooke’s law of Elasticity :
When an external force is applied to the body, the body tends to deform. If the external force is removed and the body comes back to its original position. The tendency of the body to coming back to its original position after the removal of stress is known as elasticity. The body will regain its original position after the removal of stress within a certain limit. Thus there is a limiting value of force up to which and within which the deformation disappears completely. The stress that corresponds to this limiting force is an elastic limit of the material.
Young’s modulus | Modulus of Elasticity:
The proportionality constant between the stress and strain is known as young’s modulus and modulus of elasticity.
![]()
E= Young’s Modulus
What is an example of Hooke’s law ?
Hooke’s law spring:
An important component of automobile objects , the spring stores potential elastic energy when it is stretched or compacted. The spring extension is directly proportional to the applied force within the proportionality limit.

Mathematical representation of the Hooke’s law states that the applied force is equal to the K times the displacement,
F= -Kx
Hook’s law material elastic properties can only be explained when applied force is directly proportional to the displacement.
What is the name of the substance that does not obey Hooke’s law ?
Answer : Rubber
Does Hooke’s law fails in case of thermal expansion?
Answer : No
Hooke’s law stress strain | Hooke’s law for plane strain
Hooke’s law is important to understand the behaviour of the material when it is stretched or compressed. It is important to enhance the technology by understanding the material behaviour properties.
Hooke’s law equation stress strain
F=ma
σ=F/A
ε = Δl/l0
σ = E ε
F= -k * Δx
Strain is the ratio of total deformation or change in length to the initial length.
This relationship is given by ε = Δl/l0 where strain, ε, is change in l divided by initial length , l0 .
Why do we consider a spring massless in Hooke’s law ?
Hooke’s law is dependent on the spring extension and spring constant and is independent on the mass of the spring.so we consider spring massless in Hook’s law.
Hooke’s law experiment :
The Hooke’s law experiment performed to find out the spring constant of the spring. The original length of the spring before applying load is measured. Record the applied loads (F) in N and the corresponding lengths of the spring after extension. The deformation is the new length minus the original length before loads.
Since the force has the form
F = -kx
Why is Hooke’s law negative ?
While representing hooks law for springs, the negative sign is always presented before the product of the spring constant and the deformation even though the force is not applied. The restoring force, which gives the deformation to the spring and the spring, is already in the opposite direction to that of the applied force. Thus, it is important to mention the direction of the restoring force while solving elastic material problems.
Derivation of Hooke’s Law:
Hooke’s Law equation:
F=-kx
Where,
- F=Applied force
- k=Constant for displacement
- x = Length of the object
- The use of k is dependent on the kind of elastic material, its dimensions and its shape.
- When we apply a relatively large amount of applied force, the material deformation is larger.
- Although, the material remains elastic as before and returns to its original size, and when we remove the force that we apply, it retains its shape. At times,
Hooke’s law describes the force of
F = -Kx
Here, F represents the equal and oppositely applied to restore, causing the elastic materials to get back to their original dimensions.
How is Hooke’s Law measured?
Hooke’s law units
SI units: N/m or kg/s2.
Hooke’s law spring constant
We can easily understand Hooke’s Law in connection with the spring constant. Moreover, this law states that the force required for compression or extension of a spring is directly proportional to the distance to which we compress or stretch it.
In mathematical terms, we can state this as follows:
F=-Kx
Here,
F represents the force that we apply in the spring. And x represents the compression or extension of the spring, which we usually expressed in metres.
Hooke’s law example problems
Let us understand this more clearly with the following example:
It stretches a spring by 50 cm when it has a load of 10 Kg. Find its spring constant.
Here, it has the following information:
Mass (m) = 10 Kg
Displacement (x) = 50cm = 0.5m
Now, we know that,
Force= mass x acceleration
=> 10 x 0.5= 5 N.
As per the Spring Constant formula
k = F/x
=> -5/0.5= -10 N/m.
Applications of Hooke’s law | Hooke’s law application in real life
- It is used in Engineering applications and physics.
- Guitar string
- Manometer
- spring scale
- Bourdon tube
- Balance wheel
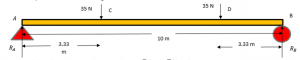
Hooke’s law experiment discussion and conclusion
Limitation of Hooke’s law:
Hooke’s law is a first-order approximation to the response of the elastic bodies. It will eventually fail once the material undergoes compression or tension beyond its certain elastic limit without some permanent deformation or change of state. Many materials vary well before reaching the elastic limits.
Hook’s law is not a universal principle. It does not apply to all the materials. It applies to the materials having elasticity. And till the material capacity to stretch to a certain point from where they won’t regain their original position.
It is applicable until the elastic limit of the material. If the material is stretched beyond the elastic limit, plastic deformation takes place in the material.
The law can give exact answers only to the material undergoing small deformations and forces.
Hooke’s law and elastic energy:
Elastic Energy is the elastic potential energy due to the stored deformation of the stretching and compression of an elastic object, such as stretching and release of the spring. According to Hook’s law, the force required is directly proportional to the amount of stretch of the spring.
Hook’s Law: F= -Kx — (Eq1)
The force applied is directly proportional to the extension and deformation of the elastic material. Thus,
Stress is directly proportional to strain as stress is the applied force to that of unit area and strain is deformation to that of the original dimension. The stress and strain considered are normal stress and normal strain.
In shearing stress,Material must be homogeneous and isotropic within its certain proportionality limits.
Shear stress represented as,
τxy = Gγxy —(Eq2)
Where,
- τxy=shear stress
- G=modulus of rigidity
- γxy=shearing strain
This relation represents Hook’s law for shear stress. It is considered for the small amount of force and deformation. Material leads to failure if applied load larger force.
Considering material subjected to shearing stresses τyz and τzy, for small stress, the γxy will be the same for both the conditions and are represented in similar ways. The shear stresses within the proportional limit,
τxy = Gγxy —(Eqn3)
τxy = Gγxy —(Eqn4)
Case1: plain strain where the strains in the z-direction are considered to be negligible,
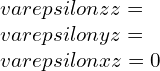
the stress-strain stiffness relationship for isotropic and homogeneous material represented as,

The stiffness matrix reduces to a simple 3×3 matrix, The compliance matrix for the plane strain is found by inverting the plane strain stiffness matrix and is given by,
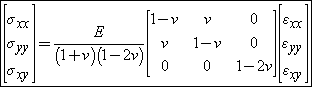
Case2:Plane strain:
The stress-strain stiffness matrix expressed using the shear modulus G, and the engineering shear strain
 is represented as,
is represented as,

The compliance matrix is,
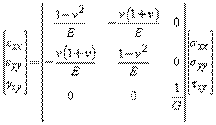
Hooke’s law Problems:
States Hookes Law What is the spring constant of a spring that needs a force of 3 N to be compressed from 40 cm to 35 cm.
Hook’s law:
F= -Kx ,
3= -K (35-40)
K=0.6
A force of 1 N will stretch a rubber band by 2 cm Assuming that Hookes law applies how far will a 5 N force stretch the rubber band
Force is directly proportional to the amount of the stretch, According to Hook’s law:
F= -Kx
![]()
F2=3cm
For more article click here


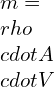
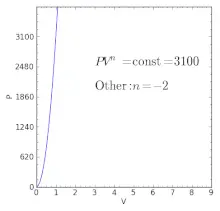

![Rendered by QuickLaTeX.com \\\\P_1V_1^n=P_2V_2^n\\\\ \\\\\\frac{P_2}{P_1}=[\\frac{V_1}{V_2}]^n](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-2f79f958a45d3de1b856d5a94f13b960_l3.png)
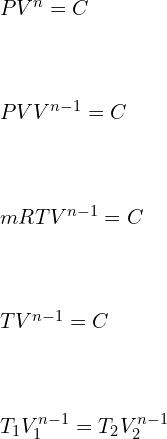
![Rendered by QuickLaTeX.com \\\\W=\\int_{1}^{2}Pdv\\\\ \\\\W=\\int_{1}^{2}\\frac{C}{V^n}dv\\\\ \\\\W=C[\\frac{V^{-n+1}}{-n+1}]^2_1\\\\ \\\\W=\\frac{P_1V_1V_1^{-n+1}-P_2V_2V_2^{-n+1}}{n-1}\\\\ \\\\W=\\frac{P_1V_1-P_2V_2}{n-1}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-34673bf8e32b5351c5b578248dee5bc8_l3.png)
![Rendered by QuickLaTeX.com \\\\dQ=mC_v [T_2-T_1 ]+\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=\\frac{mR}{\\gamma -1} [T_2-T_1 ]+\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=\\frac{P_1 V_1-P_2 V_2}{\\gamma-1}+\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=P_1 V_1 [\\frac{1}{n-1}-\\frac{1}{\\gamma-1}]-P_2 V_2 [\\frac{1}{n-1}-\\frac{1}{\\gamma-1}]\\\\ \\\\dQ=\\frac{\\gamma -n}{\\gamma -1}\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=\\frac{\\gamma -n}{\\gamma -1}W_{poly}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-30c37e1c1015acd433b3e3770a8fe0c2_l3.png)
![Rendered by QuickLaTeX.com H_p=53.3*z_{avg}*\\frac{T_s}{S}(\\frac{\\gamma \\eta _p}{\\gamma -1})[(\\frac{P_d}{P_s})^\\frac{\\gamma -1}{\\gamma \\eta _p}-1]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-9c919db20c42b8e740e81a820f601ceb_l3.png)

![Rendered by QuickLaTeX.com \\\\W=\\frac{P_1V_1-P_2V_2}{n-1}\\\\W=\\frac{mR[T_2-T_1]}{n-1}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-e851f1e9ecda47f4624cdfbe61caf7a5_l3.png)
![Rendered by QuickLaTeX.com \\\\\\frac{P_1V_1}{T_1} =mR \\\\mR=\\frac{200*10^3*0.1}{200}\\\\ \\\\mR=100 J/(kg. K) \\\\ \\\\W=\\frac{100*[400-200]}{1.22-1}\\\\ \\\\W=90.909 kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-4a2c065006d2428fe2857f0a0f21c6fa_l3.png)
![Rendered by QuickLaTeX.com W=\\frac{1*208.1[90-30]}{1.33-1}\\\\ \\\\W=37.836\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f983a3808c53dd20f2f92333dd859293_l3.png)
![Rendered by QuickLaTeX.com \\\\W=\\frac{10*63.33*[259.63-500]}{1.28-1}\\\\ \\\\W=-543.66\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f3ef4aecd99714fbc6ce8f1b80373ad1_l3.png)
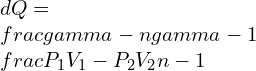

![Rendered by QuickLaTeX.com dQ=\\frac{\\gamma -n}{\\gamma -1}\\frac{mR[T_2-T_1]}{n-1}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-9623d0173cc15e05297ccd524759531a_l3.png)
![Rendered by QuickLaTeX.com \\\\dQ=\\frac{1.4 -1.15}{1.4 -1}\\frac{1*518.2*[311.52-293]}{1.15-1}\\\\\\\\dQ=39.997\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-0ddd733cda78faa73a241c473fe6bf77_l3.png)
![Rendered by QuickLaTeX.com \\\\W=\\frac{2077.1*[400-303]}{1.24-1}=839.494\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-58fbc142958923099feceb48f6431e40_l3.png)

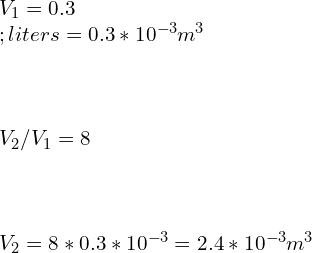
![Rendered by QuickLaTeX.com \\\\\\frac{P_2}{3}=[\\frac{0.3}{2.4}]^{1.7}\\\\\\\\P_2=0.0874\\;MPa](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-a09eba21348fdf1e95edca72e436526b_l3.png)
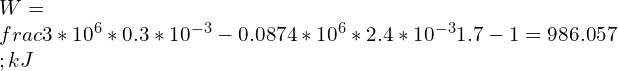
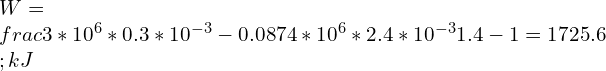
![Rendered by QuickLaTeX.com \\\\\\frac{800}{120}=[\\frac{200}{V_2}]^{1.29} \\\\\\\\V_2=45.95\\;L](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-41323679bbdf82666782c64b16cfa457_l3.png)
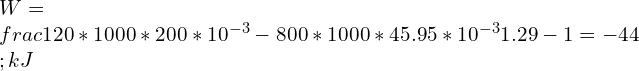
![Rendered by QuickLaTeX.com dQ=\\frac{1.4-1.1}{1.4 -1}\\frac{12*518.2*[30-150]}{1.1-1}=-5.596\\;MJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-6ebe82b84e38a99ceddb14a01559df47_l3.png)
![Rendered by QuickLaTeX.com W=\\frac{1*81.49*[100-10]}{1.33-1}=22.224\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f99d83d9c42cc7b2180db4866e1d97ed_l3.png)
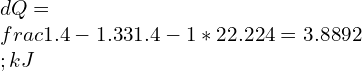





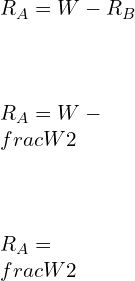



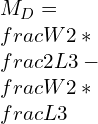
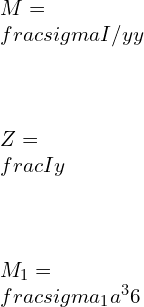
![Rendered by QuickLaTeX.com \\\\I=\\frac{bd^3}{12}*2\\\\ \\\\I=\\sqrt{2}a*[\\frac{a}{\\sqrt{2}}]^3*\\frac{2}{12}\\\\\\\\ \\\\Z=\\frac{I}{y}=\\frac{a^3}{6\\sqrt{a}}\\\\\\\\ \\\\M_2=\\frac{\\sigma _2 a^3}{6\\sqrt{a}}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-82a207ef63fe59582dca98a0a941f99d_l3.png)