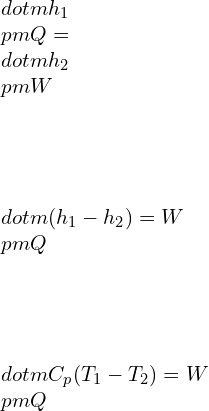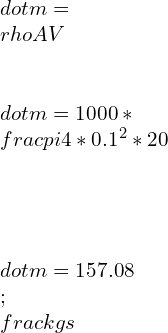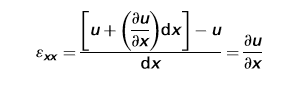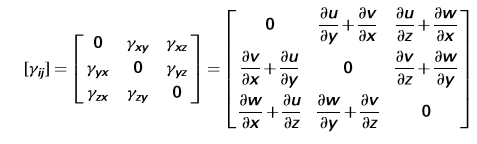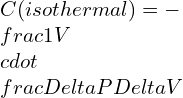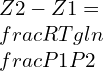What is Shear modulus ?
Modulus of Rigidity definition
Shear modulus is the ratio of the shear stress to the shear strain.
Shear modulus is defined as the measure of the elastic shear stiffness of the material and it is also acknowledged as ‘modulus of rigidity’. So, this parameter answers the question of how rigid a body is?
Shear modulus is the material response to a deformation of body because of the shearing stress and this work as ‘the resistant of the material to shearing deformation’.

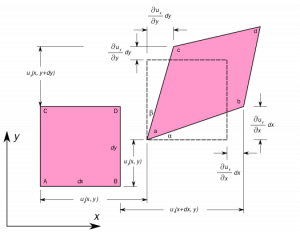
In the above figure, Side lengths of this element will not change, though the element experiences a distortion and shape of element is changing from the rectangle to a parallelogram.
Why do we calculate the modulus of rigidity of the material ?
Shear modulus equation | Modulus of Rigidity equation
Shear modulus is the ratio of the shear stress to the shear strain, which is measures the amount of distortion, is the angle (lower case Greek gamma), always ex-pressed in radians and shear stress measured in force acting on an area.
Shear modulus represented as,
G=![]()
Where,
G= shear modulus
τ=shear stress = F/A
ϒ = shear strain=![]()
modulus of rigidity symbol
G or S or μ
What is the SI unit of rigidity modulus ?
Shear modulus units | Unit of modulus of rigidity
Pascal or usually denoted by Giga-pascal. Shear modulus is always positive.
What is the dimensional formula of modulus of rigidity ?
Shear modulus dimensions:
![]()
Shear modulus of materials:
Shear modulus of steel | Modulus of rigidity of steel
Structural steel:79.3Gpa
Modulus of rigidity of stainless steel:77.2Gpa
Modulus of rigidity of carbon steel: 77Gpa
Nickel steel: 76Gpa
Modulus of rigidity of mild steel: 77 Gpa
What is the Rigidity modulus of copper in N/m2 ?
Modulus of rigidity of copper wire:45Gpa
Shear modulus of Aluminum alloy: 27Gpa
A992 Steel: 200Gpa
Shear modulus of concrete | Modulus of rigidity of concrete: 21Gpa
Silicon shear modulus: 60Gpa
Poly ether ether ketone (PEEK):1.425Gpa
Fiberglass shear modulus: 30Gpa
Polypropylene shear modulus: 400Mpa
Polycarbonate shear modulus: 5.03Gpa
Polystyrene shear modulus:750Mpa
Shear modulus derivation | Modulus of rigidity derivation
If the co-ordinate axes (x, y, z) coincides with principle axes and intended for an isotropic element, the principal strain axes at (0x,0y,0z ) point, and considering alternative frame of reference directed at (nx1, ny1, nz1) (nx2, ny2, nz2) point and in the meantime, Ox and Oy are at 90 degree to each other.
So we can write that,
nx1nx2 + ny1ny2 + nz1nz2 = 0
Here Normal stress (σx’) and the shear-stress ( τx’y’) has been computed utilizing Cauchy’s formulation.
The resultant stress vector on the plane will have components in (x-y-z) as
τx=nx1σ1.
τy=nx2 σ2.
τz=nx3 σ3.
The normal stress on this x-y plane has been computed as the summation of the component’s projections along the normal directions and we can elaborate as
σn= σx=nx^2 σ1+nx^2 σ2+nx^2 σ3.
Similarly, the shear stress component in x and y plane nx2, ny2, nz2.
Thus
τxy=nx1nx2σ1+ny1ny2σ2+nz1nz3σ3
Considering as ε1, ε2, ε3 are the principal strains and the normal-strain is in x-direction, then we can write as
εx’x’=nx1^2ε1+ny^2ε2+nz^2ε3.
The shear strain is obtained as,
![Rendered by QuickLaTeX.com \\gamma xy=\\frac{1}{(1+\\varepsilon x)+(1+\\varepsilon y)}[2\\left ( nx1nx2\\varepsilon 1+ny1ny2\\varepsilon 2+nz1nz2\\varepsilon 3 \\right )+\\left ( nx1nx2+ny1+ny2+nz1+nz3 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-cf0ff2b75b9b650d50f0eef50e392519_l3.png)
εx’=εy’

Substituting the values of σ1, σ 2 and σ 3,
![Rendered by QuickLaTeX.com \\gamma xy= [\\lambda \\Delta\\left ( nx1nx2\\varepsilon 1+ny1ny2\\varepsilon 2+nz1nz2\\varepsilon 3 \\right )+\\left ( nx1nx2+ny1+ny2+nz1+nz3 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-dab83b91fc5915165b4a1f6465aceeb9_l3.png)
τx’y’=μϒx’y’
Here, μ= shear modulus usually represented by term G.
By taking other axis as Oz¢ with direction cosines (nx3, ny3, nz3) and at right-angle with the Ox¢ and Oy¢. This Ox¢y¢z¢ will create conventional forms an orthogonal set of axes, therefore we can write as,
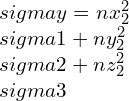
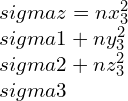

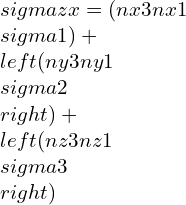
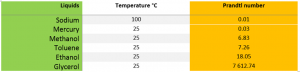
strain components,
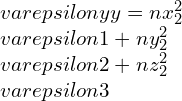
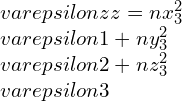
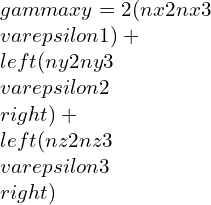
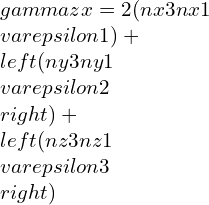
Elastic constants and their relations:
Young’s modulus E:
The young’s modulus is the measure of the stiffness of the body and acts as resistance of the material when the stress is functional. The young’s modulus is considered only for linear stress-strain behavior in the direction of stress.
E=![]()
Poisson’s ratio (μ):
The Poisson’s ratio is the measure of the deformation of the material in the directions perpendicular to the loading. Poisson’s ratio ranges between -1 to 0.5 to maintain young’s modulus, shear modulus (G), bulk modulus positive.
μ=-![]()
Bulk Modulus:
Bulk modulus K is the ratio of the hydrostatic pressure to the volumetric strain and better represented as
K=-v![]()
E and n are generally taken as the independent constants and G and K could be stated as follows:
G=![]()
K=![]()
for an isotropic material, Hooke’s law is reduced to two independent elastic constants named as Lame’s co-efficient denoted as l and m. In terms of these, the other elastic constants can be stated as follows.
If bulk modulus considered to be +ve the Poisson’s ratio never be more than 0.5 (maximum limit for incompressible material). For this case assumptions are
n = 0.5.
3G = E.
K = ∞.
⦁ In terms of principal stresses and principal strains:

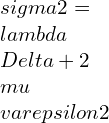
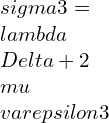
![Rendered by QuickLaTeX.com \\varepsilon 1=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma 1-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma 2+\\sigma 3 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-eb8240f97d2550c83d5b61674ea15b8b_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon 2=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma 2-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma 3+\\sigma 1 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-5916a79321f0d60e68e015fef9565945_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon 1=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma 3-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma 1+\\sigma 2 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-a7605cc38352f88f24ecedc6fe5562de_l3.png)
⦁ In terms of rectangular stress and strain components referred to an orthogonal coordinate system XYZ:
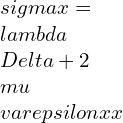
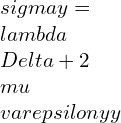

![Rendered by QuickLaTeX.com \\varepsilon xx=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma x-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma y+\\sigma z \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ba8c810228c7f208ab4b329c1ec8ba53_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon yy=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma y-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma x+\\sigma z \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-283d086fdb3111924fe0a590906dc759_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon zz=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma z-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma x+\\sigma y \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-410e232a635a25e92b2370459cbcdad0_l3.png)
Young’s modulus vs shear modulus | relation between young’s modulus and modulus of rigidity
Elastic Constants Relations: Shear Modulus, Bulk Modulus, Poisson’s ratio, Modulus of Elasticity.
E=3K(1-2 μ)
E=2G(1+μ)
E= 2G(1+μ)=3K(1-2 μ)
Shear Modulus of Elasticity:
Hook’s law for shear stress:
τxy=G.ϒxy
where,
τxy is represented as Shear-stress, Shear-modulus is G and Shear strain is ϒxy respectively.
Shear-Modulus is resistant to the deformation of the material in response to shear stress.
Dynamic shear modulus of soil:
Dynamic shear modulus gives information about dynamic one. Static shear-modulus gives information about static one. These are determined using shear wave velocity and density of the soil.

Shear Modulus Formula soil
Gmax=pVs2
Where, Vs=300 m/s, ρ=2000 kg/m3, μ=0.4.
Effective shear modulus:
The ratio of the average stresses to average strains is the effective shear-modulus.
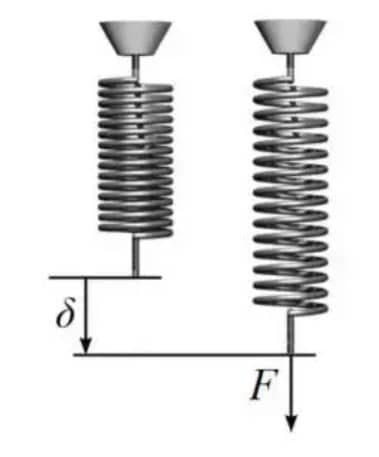
Modulus of rigidity of spring:
The modulus of rigidity of the spring is the measurement of the stiffness of the spring. It varies with the material and processing of the material.
For Closed Coil Spring:
![]()
For Open Coil Spring:
![Rendered by QuickLaTeX.com \\delta =\\frac{64WR^{3}nsec\\alpha }{d^{4}}[\\frac{cos^{2}\\alpha }{N}+\\frac{2sin^{2}\\alpha }{E}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-e7d33fd56d11bedb00c79154eebdac87_l3.png)
Where,
R= mean radius of the spring.
n = number of coils.
d= diameter of the wire.
N= shear modulas.
W= load.
δ=deflection.
α= Helical angle of the spring.
Modulus of Rigidity- Torsion | Modulus of Rigidity Torsion test
The rate change of strain undergoing shear stress and is a function of stress subjected to torsion loading.
The main objective of the torsion experiment is to determine the shear-modulus. The shear stress limit is also determined using the torsion test. In this test, one end of the metallic rod is subjected to torsion, and the other end is fixed.
The shear strain is calculated by using the relative angle of twist and gauge length.
γ = c * φG / LG.
Here c – cross-sectional radius.
Unit of φG measured in radian.
τ = 2T/(πc3),
shear-stress is linearly proportionate to shear-strain, if we measured at the surface.
Frequently Asked Questions:
What are the 3 Modulus of elasticity?
Young’s modulus:
This is the ratio of longitudinal stress to longitudinal strain and could be better represented as
Young’s modulus ϒ= longitudinal stress/longitudinal strain.
Bulk Modulus:
The ratio of hydrostatic pressure to volume strain is called the Bulk modulus denoted as
Bulk Modulus(K)=volume stress/volume strain.
Modulus of Rigidity:
The ratio of shear stress to the shear strain of the material may well characterized as
Shear Modulus(η)=shear stress/shear strain.

What does a Poisson ratio of 0.5 mean?
Passion’s ratio ranges between 0-0.5.at small strains, an incompressible isotropic elastic material deformation gives Poisson’s ratio of 0.5. Rubber has a higher bulk modulus than the shear-modulus and Poisson’s ratio nearly 0.5.
What is a high modulus of elasticity?
The modulus of elasticity measures the resistance of the material to the deformation of the body and if modulus increse then material required additional force for the deformation.
What does a high shear modulus mean?
A high shear-modulus means the material has more rigidity. a large amount of force is required for the deformation.
Why is shear modulus important?
The shear-modulus is the degree of the stiffness of the material and this analyze how much force is required for the deformation of the material.
Where is shear modulus used ?| What are the applications of rigidity modulus?
The Information’s of shear-modulus is used any mechanical characteristics analysis. For calculation of shear or torsion loading test etc.
Why is shear modulus always smaller than young modulus?
Young’s modulus is the function of longitudinal strain and shear modulus is a function of transverse strain. So, this gives the twisting in the body whereas young’s modulus gives the stretching of the body and Less force is required for twisting than stretching. Hence shear modulus is always smaller than the young’s modulus.
For an ideal liquid, what would be the shear modulus?
In ideal liquids shear strain is infinite, the shear modulus is the ratio of shear stress to the shear strain. So the shear modulus of ideal liquids is zero.
When the bulk modulus of a material becomes equal to the shear modulus what would be the Poisson’s ratio ?
As per the relation between bulk modulus, shear modulus and poissons ratio,
2G(1+μ)=3K(1-2 μ)
When, G=K
2(1+ μ)=3(1-2 μ)
2+2 μ=3-6 μ
8 μ=1
μ =1/8
Why the required shear stress to initiate dislocation movement is higher in BCC than FCC?
BCC structure has more shear stress values critical resolved than FCC structure.
What is the ratio of shear modulus to Young’s modulus if poissons ratio is 0.4, Calculate by considering related assumptions.
Answer.
2G(1+μ) =3K (1-2 μ)
2G (1+0.4) =3K(1-0.8)
2G(1.4) =3K(0.2)
2.8G=0.6K
G/K=0.214
Which has a higher modulus of rigidity a hallow circular rod or a solid circular rod ?
Modulus of rigidity is the ratio of shear stress to the shear strain and shear stress is the Force per unit area. Hence shear stress is inversely proportional to the area of the body. solid circular rod is stiffer and stronger than the hollow circular rod.
Modulus of Rigidity vs Modulus of Rupture:
The modulus of rupture is the fracture strength. It is the tensile strength of the beams, slabs, concrete, etc. Modulus of rigidity is the strength of material to be rigid. It is the stiffness measurement of the body.
If the radius of the wire is doubled how will the rigidity modulus vary? Explain your answer.
Modulus of rigidity does not vary by change of the dimensions and hence modulus of rigidity remains the same when the radius of the wire is doubled.
Coefficient of viscosity and modulus of rigidity:
The coefficient of viscosity is the ratio of the shear stress to the rate of shear strain which varies by the velocity change and displacement change and the modulus of rigidity is the ratio of shear stress to the shear strain where shear strain is due to transverse displacement.
The ratio of shear-modulus to the modulus of elasticity for a Poisson’s ratio of 0.25 would be
For this case we may consider that.
2G(1+μ)=3K(1-2 μ)
2G(1+0.25) =3K(1-0.5)
2G(1.25)=3K(0.5)
G/K=0.6
Answer = 0.6
What material has modulus of rigidity equal to about 0.71Gpa ?
Answer:
Nylon(0.76Gpa)
Polymers range between such low values.
For more Mechanical Engineering related article click here
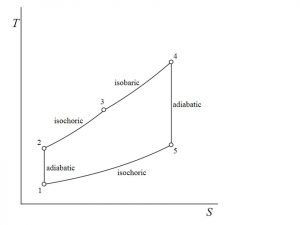
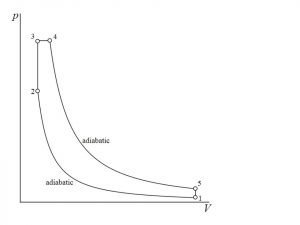
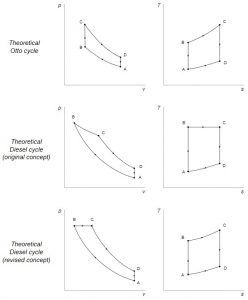
![Rendered by QuickLaTeX.com \\eta_{dual}=1-\\frac{1}{r_k^{\\gamma -1}}[\\frac{r_pr_c^\\gamma -1}{(r_p-1)+r_p\\gamma (r_c-1)}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ef5d62cb8110d7b8f13b61f35836bb06_l3.png)

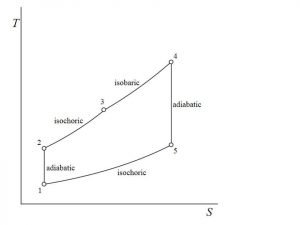
![Rendered by QuickLaTeX.com \\\\\\eta=1-\\frac{(T_5-T_1)}{([T_3-T_2 ]+\\gamma[T_4-T_3])}\\\\\\\\ \\eta_{dual}=1-\\frac{1}{r_k^{\\gamma -1}}[\\frac{r_pr_c^\\gamma -1}{(r_p-1)+r_p\\gamma (r_c-1)}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-8d7a6e6fd77001105b5968b92751f278_l3.png)
![Rendered by QuickLaTeX.com M.E.P=\\frac{(P_1 [\\gamma r_p r_k^\\gamma (r_c-1)+r_k^\\gamma (r_p-1)-r_k (r_p r_c^\\gamma-1) ] )}{(\\gamma-1)(r_k-1) }](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-b84ee279a3d25c3e77b699126299c702_l3.png)

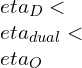

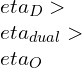

![Rendered by QuickLaTeX.com \\\\Q_v=C_v [T_3-T_2 ]=0.718*[1199-671]=379kJ/kg\\\\\\\\ (2/3)*Q=Q_v\\\\\\\\ Q=(3/2)*379=568.5 kJ/kg\\\\\\\\ C_p [T_4-T_3 ]=Q/3\\\\\\\\ 1.005*[T_4-1199]=568.5/3\\\\\\\\ T_4=1387.55 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-16101adc0e9d29571aa2ae5394d2b62b_l3.png)

![Rendered by QuickLaTeX.com \\\\r_c=[T_4/T_3 ]=[1873/1433]=1.307\\\\\\\\ Also \\;\\\\\\\\ r_c=[V_4/V_3] =1.307\\\\\\\\ V_4=1.307*0.004=5.228*10^{-3} m^3](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-b809892b3aac2d862e3a5f4e08ca9735_l3.png)
![Rendered by QuickLaTeX.com \\\\T_5/T_4 =[V_4/V_5] ^{\\gamma-1}\\\\\\\\ (T_5/1873)=[\\frac{(5.228*10^{-3})}{0.07}]^{1.4-1}\\\\\\\\ T_5=663.48 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-3c2788b7142d2658ebd2be9ada56a46a_l3.png)
![Rendered by QuickLaTeX.com \\\\Q_s=C_v [T_3-T_2 ]+C_p [T_4-T_3 ]\\\\\\\\ Q_s=0.717*(1433-942.6)+1.005*(1873-1433)\\\\\\\\ Q_s=793.81 kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-e98662763e1036e6adb2d3e4c2f5db76_l3.png)


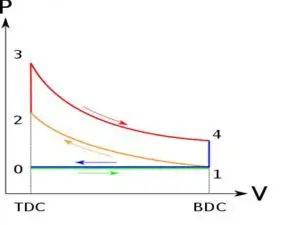


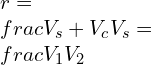


![Rendered by QuickLaTeX.com \\\\\\eta=1-\\frac{[T_4-T_1]}{[T_3-T_2]}\\\\\\\\ \\frac{T_2}{T_1}=\\frac{T_3}{T_4}\\\\\\\\ \\frac{T_4}{T_1}=\\frac{T_3}{T_2}\\\\\\\\ \\eta=1-\\frac{1}{r^{\\gamma-1}}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f49c7bd3e52c0f607a4e2c504e1ab46b_l3.png)

![Rendered by QuickLaTeX.com \\\\1000=0.717*[473-1188+T_3-T_4]\\\\\\\\ 1000=0.717*[473-1188+2.512 T_4-T_4]\\\\\\\\ T_4=1395 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-7b3a245ad98e31383d6f4d9583e34a18_l3.png)
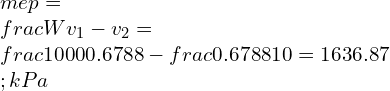
![Rendered by QuickLaTeX.com \\\\\\frac{\\mathrm{d} C_v}{C_v}=0.02\\\\\\\\ \\eta=1-\\frac{1}{r^{\\gamma -1}}=1-\\frac{1}{6^{1.4 -1}}=0.511\\\\\\\\ \\gamma -1=\\frac{R}{C_v}\\\\\\\\ \\eta=1-[\\frac{1}{r}]^\\frac{R}{C_v}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-757291f702fb1983830f344901562518_l3.png)
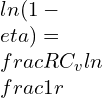
![Rendered by QuickLaTeX.com \\\\\\frac{d\\eta}{1-\\eta}=\\frac{-R}{C_v^2}*dC_v*ln[1/r]\\\\\\\\ \\frac{d\\eta}{1-\\eta}=\\frac{-R}{C_v}*\\frac{dC_v}{C_v}*ln[1/r]\\\\\\\\ \\frac{d\\eta}{\\eta}=\\frac{1-\\eta}{\\eta}*\\frac{-R}{C_v}*\\frac{dC_v}{C_v}*ln[1/r]\\\\\\\\ \\frac{d\\eta}{\\eta}=\\frac{1-0.511}{0.511}*\\frac{-0.287}{0.718}*0.02*ln[1/6]\\\\\\\\ \\frac{d\\eta}{\\eta}=-0.0136\\\\\\\\ \\frac{d\\eta}{\\eta}*100=-0.0136*100=-1.36\\%](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ef306304ee4e226f05089530564c7534_l3.png)

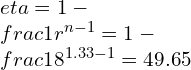
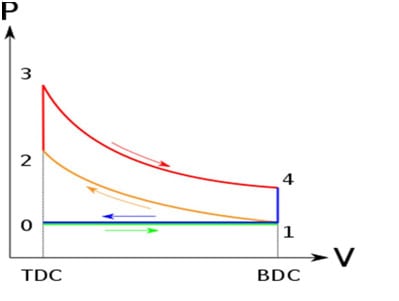


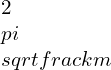
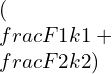
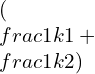

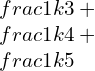
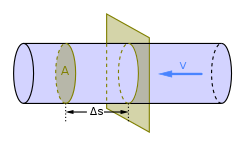
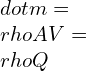
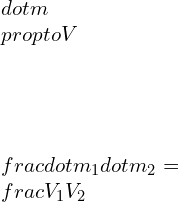
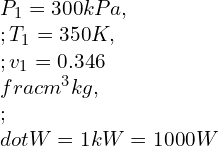
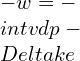
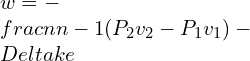
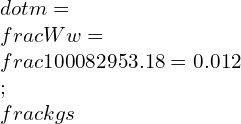
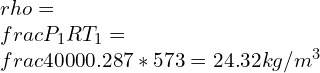
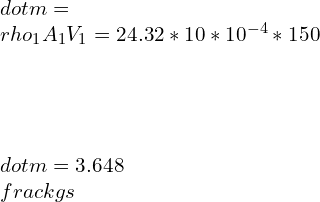
![Rendered by QuickLaTeX.com \\\\\\dot{m}h_1+Q=\\dot{m}h_2+W\\\\ \\\\\\dot{m}[h_1-h_2]=W-Q\\\\ \\\\\\dot{m}C_p[T_1-T_2]=W-Q\\\\ \\\\\\dot{m}=\\frac{W-Q}{C_p[T_1-T_2]}=\\frac{4600+300}{1100-400}=7\\;\\frac{kg}{s}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ab801810045c79c44023956f8f7184db_l3.png)


![Rendered by QuickLaTeX.com \\\\P=\\dot{m}[h_1-h_2]\\\\ \\\\\\dot{m}=\\frac{P}{h_1-h_2}\\\\ \\\\\\dot{m}=\\frac{P}{C_p[T_1-T_2]}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f9d3656cc8e9eecbd79512180f849452_l3.png)