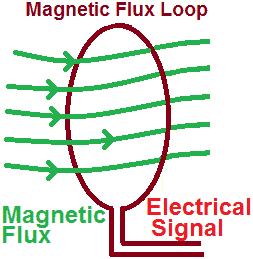
Every magnetic regardless of shape and size, has two poles from which imaginary lines pass between the two poles, called magnetic flux. Here facts on magnetic flux example are given.
- Earth’s magnetic field
- The magnetic field of celestial stars
- Mariner’s compass
- Bar magnets
- The magnetic field between two magnets
- MRI scanners
- Microwave oven
- The magnetic field of planets
- The magnetic field in motors
- Magnetic filed in an electronic device
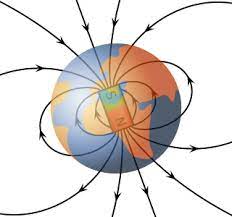
Earth’s magnetic field
Our earth is a giant magnet whose field lines are outrageous from the core to space. The earth’s magnetic flux lines shield the earth by avoiding space dust and harmful solar radiation.
The magnetic field of celestial stars
The celestial stars, like the sun consist of a magnetic field due to the motion of conductive plasma inside them. A neutron star consists large magnetic field.
Mariner’s compass
The navigation can possibly use a compass only due to the magnetic field. It consists of a set of magnetic needles that generate flux lines and help determine direction. The needle points in the direction of the opposite polarity to determine the direction.
Bar magnets
We know that every magnet are of bi-poles, a south pole, and a north pole. The magnetic fields are generated around the bar magnet in such a way that the flux lines flow from the north to the south pole.
Image credits: Wikimedia commons
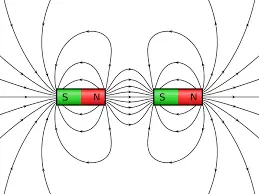
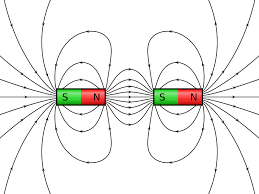
The magnetic field between two magnets
When two magnets are placed nearer to each other, the magnetic field is generated between them. These magnetic fields are responsible for the attraction and repelling ability of the magnet. If opposite poles are facing each other, both magnets are attracted. If like poles are facing each other, they repel.
MRI scanners
The working principle of MRI scanners depends on the magnetic field. The scanner consists of a large magnet that generates a magnetic field. These magnetic fields are used to imagine the human body and detect a fault.
Microwave oven
The microwave oven generates a magnetic field that can oscillate back and forth 4.9 billion times every second. This oscillation causes the molecules to flip and produces friction, generating heat utilized for cooking the food item.
The magnetic field of planets
Most of the planet has a magnetic field that may be strong or weak. These fields help the planet for stable rotation around the sun and protect the planet from radiation.
The magnetic field in motors
All the motors are provided with rotating magnets which helps the machine to be in sync with the speed of air. The magnetic field enables the motor to run efficiently.
Magnetic filed in an electronic device.
Every electronic device produces a magnetic field by electric field. The motion of the charges generates the magnetic field in the machine. The magnetic field in an electronic device is temporary and disappears as soon as the current is turned off.
How to use magnetic flux?
Magnetic flux is determined by considering the area occupied by field lines that pass through a closed surface and the direction of orientation of the lines.
Since magnetic flux generally represents the lines that pass between the two poles in a closed-loop, the area of the loop must be known to use the magnetic flux. The magnetic flux is a tool to describe the effect of the magnetic force on anything under the influence of a magnetic field; thus particular area must be chosen for the magnetic flux.
The formula gives the magnetic flux
φB=B.A=B.A cos θ
Where B is the magnetic field, A is an area of the region, and θ is the angle made by the magnetic field on the region.
The bare eyes cannot see the magnetic flux, but it can be visualized using the iron filings sprinkled on paper.
When to use magnetic flux?
T0 illustrate the effect of a magnetic field passing through a region or closed space, the magnetic flux is used. Since the area of the region where the magnetic field lines are passing contributes to the magnetic flux, the angle at which the line intersects the area is also important.
When we calculate the magnetic flux, the glancing angle contributes to the magnetic flux.
- When the angle between the magnetic field and area vectors are normal to each other, i.e., 90°, the flux passing through the region is low.
- If the angle is 0°, the probability of flux passing between the pole pieces is more.
This illustrates the effect of magnetic field force exerted on that region of space.
Image credits: Wikimedia commons
9 Magnetic Flux Examples
- Magnetic flux in a solenoid
- Magnetic flux in the transformer
- Magnetic flux lines around the earth
- Magnetic flux in a wire loop
- The magnetic flux of the coil
- The magnetic flux of toroid
- The magnetic flux of a bar magnet
- Magnetic flux in electric motors
- Magnetic flux in magnetic circuits
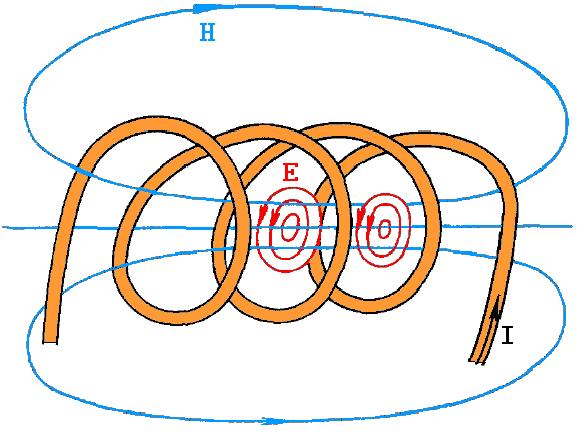
Magnetic flux in a solenoid
Since we know that magnetic flux is the number of magnetic field lines on a closed surface, solenoid consists of the uniform magnetic field, which produces maximum flux directed along the length of the coil.
Magnetic flux in the transformer
The transformer’s primary coil induces the current in the core to oppose the charges, creating a magnetic flux. This magnetic flux acts as a linkage that binds both the winding together when there is an increase or decrease in the AC power supply in the opposite direction.
Magnetic flux lines around the earth
The earth’s magnetic flux is invisible lines always directed south to the north pole. These flux lines trap the unwanted radiation and create a magnetosphere around the earth as a shield.
Magnetic flux in the wire loop
Magnetic flux is created if a magnet moves towards the wire loop. These fluxes are in a downward direction and increase with the current. The magnetic fields are always in the opposite direction and oppose the flux. If the loop is closed, the total magnetic flux in the loop is zero because the number of field lines entering and leaving the loop is the same.

Image credits: Wikimedia Commons
The magnetic flux of the coil
A moving coil generates the magnetic field and magnetic flux in the opposite direction. The change in magnetic environment causes emf in the coil. The change in magnetic flux in the coil is associated with the voltage to be induced. The induced voltage is always negative of the change in magnetic flux.
The magnetic flux of toroid
Toroids are donut-shaped coils made of powdered iron. These are used as an inductor to operate at low frequency in circuits. When the current is passed, magnetic fields are generated inside the coil, and the magnetic field outside the coil is zero.
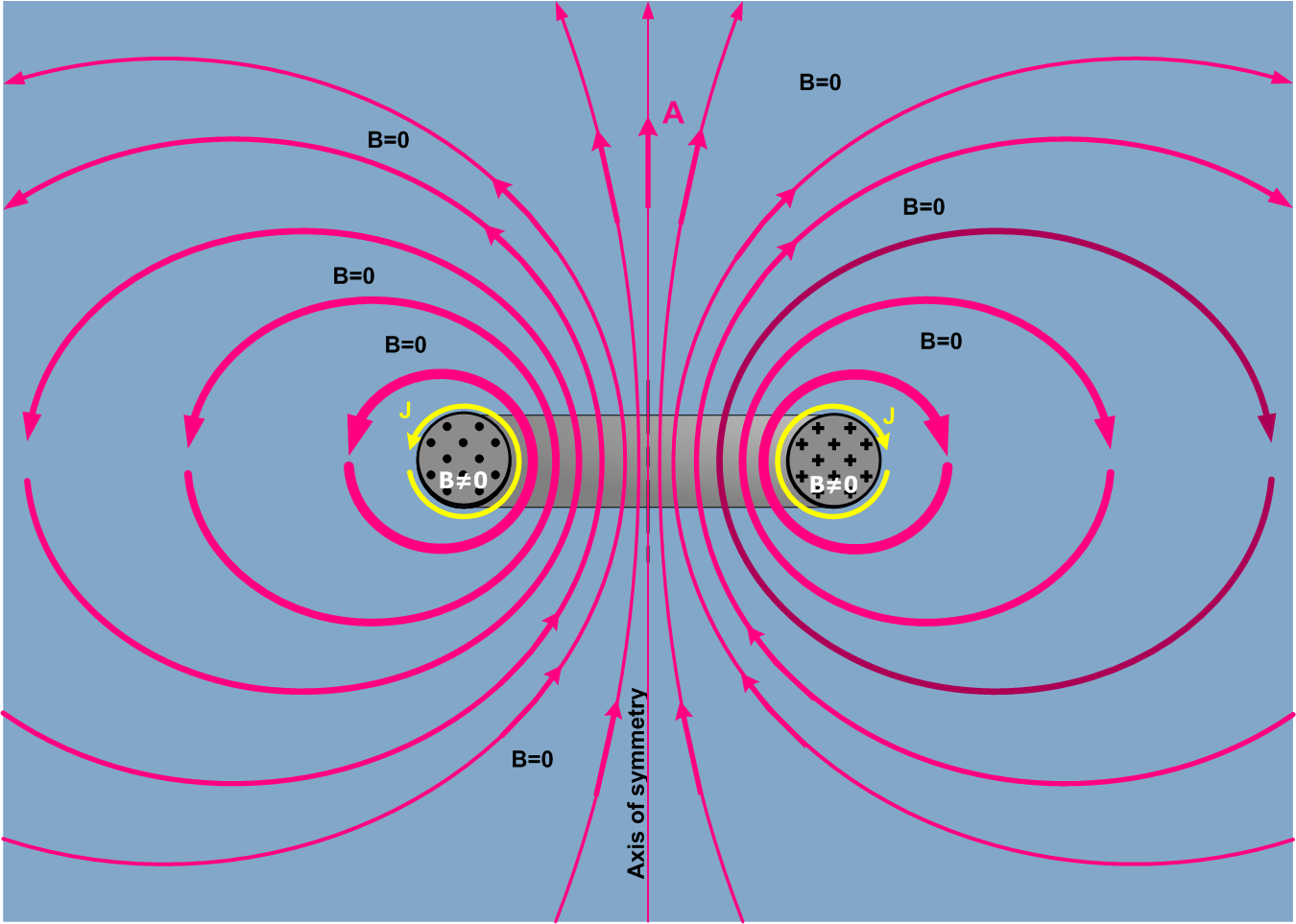
Image credits: Wikimedia commons
The magnetic flux of a bar magnet
In a bar magnet, the magnetic flux is always directed north to the south pole. The flux creates a closed-loop structure around the magnet. The magnetic flux around the bar magnet will be zero if the magnetic field is parallel to the area.
Magnetic flux in electric motors
The permanent magnets fitted inside the electric motor generate the magnetic flux. The flux can boost or oppose the action of the motor. The boosting flux helps the motor to increase the torque, and the opposing flux makes the motor run with an existing magnetic field.
The magnetic flux generated in the DC motor is due to the magnetic field’s rotating loop through the electromagnetic induction process.
Magnetic flux in magnetic circuits
A magnetic circuit is made up of more than one closed-loop magnetic component consisting of magnetic flux. The ferromagnetic materials such as iron and nickel confine the path of the magnetic field, and thus, magnetic flux is generated.
This flux efficiently channels the magnetic field in other devices. These flux flow through the area perpendicular to the magnetic field. The magnetic flux through the magnetic circuits drives the magneto-motive force through the circuit.
Conclusion
Let us wrap up this post by stating magnetic flux is vector quantity which associated with the direction of the magnetic field. These are invisible imaginary lines which describes the intensity and direction of the magnetic field. The real world magnetic flux example give an account on behavior of these imaginary lines.
Also Read: