Effect - lambdageeks.com

3 Facts On Doppler Effect For Light:What,How,Examples & FAQs

January 20, 2024January 5, 2023 by Alpa P. Rajai

The Doppler effect applies to both sound waves as well as light waves. So let us first analyze what the doppler effect of light is. The Doppler effect of light is defined as the change in the frequency of light viewed by the observer as a result of the relative motion of the observer and … Read more

15 Doppler Effect Examples: Detailed Explanations

January 20, 2024March 21, 2022 by AKSHITA MAPARI

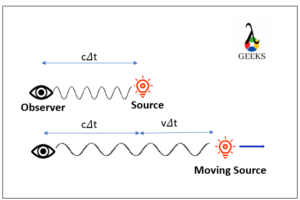
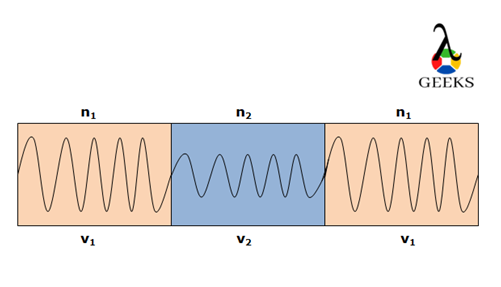
The relative change in the frequency of the sound or light due to the motion of the observer and the source, this effect is termed as a Doppler effect after a scientist Christian Doppler. We shall discuss a few doppler effect examples below.

As the distance between the source and the observe decreases, the wavelength becomes shorter and frequency increases,

and if the distance between both increases the frequency decreases

, where v is a velocity of sound, f is a change in frequency, f₀ is a actual frequency, v₀ is a velocity of object, v_s is a velocity of source.

Vehicle Running on the Road

You must be familiar with the phenomenon of a Doppler Effect due to the moving vehicle in speed.

doppler effect examples — **Doppler Effect due to the vehicles in motion; Image Credit: Pixabay**

If you are standing on the roadside, you must have heard the variation in the sound wave of approaching vehicle and after it recedes away from you.

Trumpet

If you pass by a trumpet player, you will notice a variation in the sound as you walk away from the trumpet player. This is due to the Doppler Effect.

As you walk away, the distance between the source and the receiver increases thus decreasing the frequency of the sound of notes received by you.

Ultrasonic Sensor

The ultrasonic sensor generates and emits a wave; which is received back when these waves reflect on hitting the obstacles. This is used to detect the water level, distance from the obstacles, depth of the water, etc.

robot g32c72b18d 640 — **The ultrasonic sensor clamped on servo motors; Image Credit: Pixabay**

RADAR

Radio Detection and Ranging is devices used to detect obstacles from a far distance using electromagnetic waves. The waves received back on reflecting from the surface of the obstacle in case the obstacle comes in a range of the device.

sailor gf060a496d 640 — **RADAR technique used by sailors; Image Credit: Pixabay**

There are different software used to read the distance and the location of the obstacles from the source. RADARs are used as navigators for ships and airplanes during bad weather conditions.

Astronomy

Doppler Effect has also made it possible to calculate the distance of the comet or asteroids approaching the Earth. The variation in the frequency of the waves from the heavenly body can be used to determine the velocity of the body and the distance at which it is present.

Resonance from Pipe

A sound wave produced at one end of the pipe will set up the vibration in the air molecules inside a volume of a pipe producing a region of contraction and rarefaction. Due to this, the frequency of a sound wave will frequently differ.

Train

If you hear a sound of a whistle from a train approaching a station, the frequency of the sound decreases as the train pass by you. This is due to the Doppler Effect.

blur g6ddb51fc7 640 — **Whistle of a Train approaching the station; Image Credit: Pixabay**

Ambulance Sirens

If you are driving a vehicle in a lane and you hear a sound of a siren of an ambulance approaching you, the sound frequency will keep on increasing gradually until it pass by you and then the sound frequency reduces.

ambulance ged4211511 640 — **Sound waves from Ambulance Serin; Image Credit: Pixabay**

Blowing Horns

A bus driver overtaking a truck blows the horn for a while until it overtakes. The frequency of a horn heard by the truck driver before overtaking and after is different. While approaching the truck, the sound heard by the truck driver was of frequency

and once it overtakes the truck, the frequency of the sound now heard by the truck driver is

Music Instruments

When you heard nice pleasant music being played, and you try to follow the music from where it is played to find out who is the one playing such splendid music, you know that the frequency of the music keeps on increasing. In case it decreases then it is certain that you are moving on the wrong path away from your goal.

live music g0c2a56f08 640 — **Music Concert in Auditorium; Image Credit: Pixabay**

Person Shouting from the Valley Top

Consider a person standing on the top of the hill and talking in a loud voice with a person standing down the hill. The sound heard by the person and the actual frequency of a person on the hill will be different. This is also due to the Doppler Effect.

Loudspeaker in a Room

The amplified sound emerging from the loudspeaker will emit the audio waves in all directions. The sound waves received by the listener sitting at different areas in the room will receive different numbers of audio waves and thus different frequencies. Also, the person standing behind the loudspeaker will receive the reflected wave thus sound waves of low frequency.

Boating in a Pond Water

Suppose there is a square shape pond and two people are standing exactly opposite to each other at pole A and pole B respectively and a group of people are on a paddleboat in a pond. The boat is traveling from pole A to B.

Capture 2 — **A boat traveling from pole A to B**

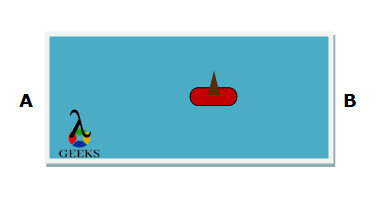
As the boat crosses halfway, a person standing at pole A will see that the speed of the boat is reduced than its actual speed and a person at pole B will see that boat is traveling slightly at a greater speed than its normal speed. This is due to the Doppler Effect.

River Side

If there is a noise from the land across the river, the frequency of the audio waves received at all the points at different angles will vary greatly.

Music Band Passes by the Roadside

The sound frequency increases steadily as the band cross by the roadside and then decreases gradually as the band recedes away from you.

Frequently Asked Questions

Does the Doppler Effect of sound, waves, or light depend upon the distance?

The Doppler Effect relies upon the distance between the source and the receiver.

The frequency of the waves differs as the distance between the two changes. The frequency of the waves is higher when the distance between the two is lessening whereas the frequency decreases as the spacing between the two rises.

What is reverberation?

It is a resonance of sound waves heard for a prolonged time.

It is due to the echoing that is the reflection of sound waves on hitting the obstacles and the waves are thrown back and received by the listener; that is the audio wave passes back to the source.

Read more about Doppler Effect For Moving Observer.

Also Read:

Effect Of Wavelength On Refraction:

January 20, 2024February 5, 2022 by AKSHITA MAPARI

$Effect Of Wavelength On Refraction: 17$

In this article, we will discuss the effect of wavelength on refraction, how does the refraction of the waves affect by the wavelength with detailed facts.

The wavelength governs the speed of the propagating wave in the medium. Depending upon the speed of the wave and the refractive index of the medium, it bends in the medium and gets refracted.

Does Wavelength Affect Refraction?

The wavelength of the propagating wave is directly correlated to the velocity of the light or a particle traveling in a wave.

The incident wave on the medium having a refractive index ‘n₁’ traveling at a speed ‘v’ and wavelength λ will refract according to the variations of the wavelength while propagating in the medium of a refractive index ‘n₂’.

The refractive index of the medium is related to the speed of the light by the equation

n=c/v

Where n is a refractive index of the medium

C is a speed of light, c=3*10⁸m/s

And v is velocity of the light on refraction

If the wavelength of the beam of particles increases, then the frequency, and thereof the energy of the particles decrease. It is evident that the wavelength of the light on refraction does not change, that is the wavelength of the light before and after the refraction of the same light is the same.

But, the speed of the propagation of the wave depends upon the wavelength of the light. The relation between the speed and the wavelength of the light is formulated as

f=v/λ

Where f is a frequency of light

V is a velocity and

λ is a wavelength of the light

The energy of the particle is directly proportional to the frequency of the oscillating particle, and is given by the equation,

E=hf

Where ‘h’ is a Planck’s Constant, h=6.626*10^-34J.s

The longer the wavelength, the less will be the energy associated with the particle, and thus the speed of the particle will be less. The particle traveling with a smaller wavelength will have higher energy pertaining to the particle and hence will travel with higher velocities.

Example: A photon of energy 0.58 MeV is incident on the medium having refractive index 1.33. Find the wavelength of the incident photons.

Given: n=1.33

E=0.58MeV=0.58*10⁶*1.6*10^-19=0.93*10^-13Joules

h=6.626*10^-34 J.s

The energy of the photon is equal to

E=hf

Hence, the frequency of the photon is

f=E/h

=0.93*10^-13/6.626*10^-34

=0.14*10²¹

=140*10¹⁸

=140EHz

The frequency of the photon is 140EHz.

The refractive index of the medium is the ratio of change in the speed of light.

n=c/v

Hence, the velocity of the light is

v=c/n

=3*10⁸/1.33

=2.25*10⁸m/s

The speed of the photon is 2.25*10⁸m/s

Therefore, the wavelength of the photon is

v=fλ

λ=v/f

=2.25*10⁸/140*10¹⁸

=0.0161*10^-10

=1.61*10^-12=1.61pm

Hence, the wavelength of the photon in the medium of refractive index 1.33 is 1.16 pm.

How does Wavelength affect Refraction?

The propagation of the wave in any medium is defined by the length of the wave, its time period, and the frequency of the particle in a wave.

Though the wavelength does not change drastically on refraction, the speed of the particle relies upon the wavelength. If the wavelength is more, the speed will be less; and the speed acquired by the particle is high if the wavelength is very less.

If the light of the greater wavelength is incident, then the refracted beams of particles will possess less energy, and hence the speed of light will be reduced and refract at smaller angles.

effect of wavelength on refraction — **Refraction of light**

If the beam of the particle of a smaller wavelength is incident, then the particle will possess higher energy, and hence on refraction, the beam of the particle will have a sufficient speed to travel at a certain speed and refract at greater angles.

Read more on Types Of Refraction: Comparative Analysis.

How does Wavelength affect Angle of Refraction?

The wavelength of the light affects the speed and the frequency of the wave.

If the wavelength is bigger, then the speed of the light will be smaller and the light will reflect at a smaller angle; and if the wavelength is small then the light will reflect at the greater angle.

Consider a light incident from the medium 1 of refractive index ‘n₁’ on the surface of the object having a refractive index ‘n₂’. The refractive index is the ratio of change in the speed of light while propagating from medium 1 to medium 2.

n₁₂=v₂/v₁

Where n₁₂ is the ratio of the refractive index of the medium 1 to medium 2,

v₁ is a speed of light in medium 1

v₂ is a speed of light in medium 2

The velocity of the light is related to the wavelength by the relation

v=fλ

At a constant frequency of light, if λ₁ and λ₂ are the wavelength of the light traveling from medium 1 to medium 2 respectively, then the refractive index of the medium is related to the wavelength as,

n₂/n₁=λ₂/λ₁

By Snell’s Law,

n₁sin θ_i = n₂ Sin θ_r

n₁/n₂=sin θ_i/sin θ_r

Hence, relating to the above equation,

λ₂/λ₁ =sin θ_i/sin θ_r

sin θ_r=λ₂λ₁/sin θ_i

θ_r=Sin^-1 λ₂λ₁/sin θ_i

The refractive angle depends upon the variations in the wavelength of the light and the incident angle of the beam as per the above equation.

Read more on Refraction.

Frequently Asked Questions

What is the angle of refraction if the light beam of a wavelength of 450nm is incident on the medium of refractive index 1.33 at an angle of 45 degrees?

Given: n₁=1

n₂=1.33

λ₁ =450nm

We know that,

n₁/n₂=λ₂/λ₁

1/1.33=λ₂/ 450nm

λ₂=450nm/1.33

λ₂=338.34nm

Hence, the wavelength of the light in the medium decreases to 338.34.

The refractive angle of the light is

θ_r=Sin^-1 λ₂λ₁/sin θ_i

θ_r=Sin^-1 338.34*450/sin 45

θ_r=Sin^-1 338.34*450/ (1/√2)

θ_r=Sin (-1)/ (0.53)

θ_r=35.56

The light refracts at 35.56 degree angle.

How does the speed of the wave change on refraction?

As the light enters the denser medium, the speed of the wave decreases.

The frequency of the light decreases on entering the denser mediums and hence the energy reduces reducing the speed of light.

Does the angle of refraction depend upon the speed of the light?

If the wavelength of the particle is small, then the particle possesses high speed.

The greater the speed of the wave, the light will bend at a bigger refractive angle.

Also Read:

Effect Of Refraction On Frequency: How, Why Not, Detailed Facts

January 20, 2024January 21, 2022 by AKSHITA MAPARI

$Effect Of Refraction On Frequency: How, Why Not, Detailed Facts 19$

In this article, we will discuss the effect of refraction on frequency, how does the frequency is affected by refraction, with detailed facts.

As a wave propagates from one medium to another, the speed of a wave changes, and hence the wavelength also varies. Due to this, the wave changes its direction of propagation making an angle of refraction.

What is Refraction?

A wavelength of light, sound, or any vibrations that traverse inside the medium is called refraction.

On refraction, the direction of the wave changes and propagates at an angle of refraction depending upon the density, temperature, and pressure gradient of the medium.

Read more on Types Of Refraction: Comparative Analysis.

Does Refraction Affect Frequency?

A wave of a certain amplitude propagating from two different mediums, the amplitude of wavelength varies depending upon the density of the medium through which it travels.

If the wave travels from a rarer to a denser medium, the speed of the wave decreases and the amplitude of the wavelength also diminishes. The same is reversed when a wave travels from denser to the rarer medium.

The speed of the wave is given by the equation

Speed=Frequency*Wavelength

v=f*λ

Where v is a speed of a wave

f is a frequency of the wave

λ is a wavelength

As the speed of the wave increases or decreases, the wavelength also increases or decreases respectively, and hence the frequency of the wave remains unchanged.

Consider a wave traveling from two different mediums. Let n₂>n₁, that second medium be denser than medium 1.

Effect of refraction on frequency — **Variation in wavelength during propagation from two different mediums**

As the wave propagates from medium 1 having refractive index n₁ to medium 2 with refractive index n₂, the speed of the wave decreases because medium 2 is denser than medium 1 and the amplitude of the wave also reduces. Again, as the wave passes back to the previous medium, that is from denser to rarer medium, the wavelength and the speed of the wave increase back. In the process, the frequency of occurrence of the nodes of the wave remains the same.

Does Index of Refraction affect Frequency?

The index of refraction determines the angle of refraction while traversing from one medium to another.

The speed of the wave in the medium depends upon the refractive index of that medium, but the frequency of the wave remains unaffected by the refractive index.

The refractive index of the medium is stated by the equation as

n=c/v

Where n is a refractive index of the medium

c is a speed of light, c=3* 10⁸m/s

v is a speed of light in medium

If the speed of the light decreases while propagating from the medium then this implies that the index of refraction is greater than 1.

In a vacuum, the speed of light remains the same and therefore the refractive index of the vacuum is one, and a ray of light travels making 180⁰ angle.

If the refractive index of the medium is greater than 1 then the wavelength of the wave reduces; and while traveling from denser to rarer medium, the wavelength increases, but the frequency of the wave remains the same.

Read more on Refractive Index.

Is Refraction Affected by Frequency?

The frequency of the wave does not change after refraction.

The refractive index of the wave is directly proportional to the permittivity of the medium and determines how fast the wave can travel through the medium. The permittivity depends upon the frequency of wavelength in the medium.

We can talk about the permittivity of the medium based on the density that significantly decides the velocity of the wave in the medium. In a rarer medium, permittivity will be more because the frequency of the light will be reduced as the wavelength will increase. The velocity of the wave will increase hence the refractive angle will be more.

In a medium having less permittivity, the frequency of the wave propagating from the medium will be more, hence the wavelength will be less, the velocity of the wave will decrease and the wave will refract at the smaller angle. This is in the case of a denser medium.

Why does refraction not affect Frequency?

The frequency of the wave propagating from different mediums does not change.

The energy of the wave is conserved before and after the refraction, which implies that the frequency of the wave remains unaffected.

The energy associated with the wave is given by the equation

E=hf=hv/λ

As the speed of the wave increases or decreases based on the permittivity of the medium, the wavelength of the wave also increases or decreases respectively, and therefore the frequency remains unaffected.

Speed is directly proportional to the wavelength propagating in space. While propagating from mediums having different densities, the speed, the amplitude, and hence the wavelength of the wave differs, but the number of waves occurring per unit time remains the same even after refraction.

Does Frequency Affect Angle of Refraction?

The angle of refraction depends upon the change in the speed of the wave varied while traveling from one medium to another.

Based on the density of the medium the speed of wave varies and diverts at a particular angle on refraction.

Consider a light wave is propagating from air to glass then the refractive index of the medium is given by Snell’s Law as

n_air/n_glass=sinθ_r/sinθ_i

The refractive index is directly proportional to the speed of the wave in different mediums while propagating, then

n_air/n_glass=v₂/v₁

Hence,

v₂/v₁=sinθ_r/sinθ_i

The angle of refraction depends upon the speed of light after refraction and the angle of incident depends upon the speed of the incident light.

As, the speed is product of the wavelength and the frequency, we can write

v₂/v₁=λ_2f/λ_1f

Frequency of the light remains the same after refraction, therefore,

v₂/v₁=λ_2f/λ_1f

That is,

sinθ_r/sinθ_i=v₂/v₁=λ₂/λ₁

For a constant wavelength, the velocity of the wave will increase by increasing the frequency of the wave, and the wave will refract at a greater angle after refraction. If the frequency is less, then the speed of the wave will be deduced and the refractive angle will be smaller.

Frequently Asked Questions

Does the wavelength of the light vary in the vacuum?

The wavelength of the light directly corresponds to the speed of the light.

The speed of the light does not change while traveling through a vacuum, that is v=c, hence the refractive index n= c/v = 1. Since v remains constant, the wavelength is also constant.

Does the temperature affect the refraction of the light?

The refraction of the light depends upon the refractive index, the density, the permittivity of the medium, and the temperature too.

If the temperature rises then the density of the medium drops and the speed of the wave in the medium will increase. Hence, the refracted ray will get diverted making a greater angle with normal.

Also Read:

Mastering Robot End Effectors: A Comprehensive Guide

June 18, 2024March 16, 2021 by Esha Chakraborty

Robot end effectors are the crucial components that enable robots to interact with their environment and perform a wide range of tasks. These specialized tools, attached to the end of a robot’s arm, are responsible for manipulating objects, applying forces, and executing complex motions. In this comprehensive guide, we will delve into the technical specifications, modeling, control, and human-robot interaction aspects of robot end effectors, providing a valuable resource for science students and robotics enthusiasts.

Technical Specifications and Modeling

The technical specifications of robot end effectors are crucial in determining their capabilities and performance. These specifications include the end effector’s size, weight, payload capacity, degrees of freedom, and the range of motion. Understanding these parameters is essential for designing and selecting the appropriate end effector for a given application.

One key aspect of end effector modeling is the representation of human motor control and adaptivity. Researchers have proposed that models of human control can be applied to the modeling of action performance regularities in robotics problems where the position and kinematics of the end-effector are crucial. This approach involves modeling the skill developed in experimental tasks as a hidden Markov process, with the velocity curve acquired during the experiment considered as observable symbols and different states modeling the velocity as the trial progresses. This model can be used to represent a prototypical execution of the task, which can be queried by the robot to reproduce the movement and calculate the desired end-effector variables.

The mathematical representation of this model can be expressed as follows:

π = [π₁, π₂, ..., πN]
A = [aij]
B = [bj(k)]

Where:
– π is the initial state distribution
– A is the state transition probability matrix
– B is the observation probability matrix
– N is the number of states
– aij is the probability of transitioning from state i to state j
– bj(k) is the probability of observing symbol k in state j

By leveraging this model, robots can learn and reproduce the prototypical execution of a task, enabling them to adapt their end-effector movements to different sensory conditions and environmental constraints.

Control and Adaptation

The control and adaptation of robot end effectors are crucial for their effective and safe operation. One approach discussed in the sources is the use of admittance control for rehabilitation robots. Admittance control is a type of force control that allows the robot to adapt its behavior based on the interaction forces with the user.

The kinematic analysis and admittance control of a rehabilitation robot can be represented mathematically as follows:

M_d * ẍ + B_d * ẋ + K_d * x = F_ext

Where:
– M_d, B_d, and K_d are the desired inertia, damping, and stiffness parameters, respectively
– x, ẋ, and ẍ are the position, velocity, and acceleration of the end-effector
– F_ext is the external force applied by the user

By adjusting the desired parameters M_d, B_d, and K_d, the robot can provide the appropriate level of assistance or resistance to the user, enabling active range of movement, accurate and smooth movements, and interactive force control. The correlation between these parameters and the Fugl-Meyer Upper Extremity (FMU) assessment score can be used to quantify the rehabilitation progress.

Quantifiable Data and Human-Robot Interaction

Understanding the human’s physical and mental state during active physical human-robot interaction (pHRI) is crucial for developing effective and safe robot end effectors. Researchers have explored the possibility of quantifying these states using various sensors and data analysis techniques.

One study formulated hypotheses related to the impact of unanticipated robot actions on the user’s physical and physiological data, as well as the relationship between these data and the user’s personality. The study found significant differences in factors such as:

Forces applied on the robot
Blinking duration and rate
Feelings of dominance
Hand position

between those who understood and did not understand the intention of the robot. These findings highlight the importance of considering the user’s state and perception during the design and operation of robot end effectors.

Clustering Analysis and Real-time Data

The integration of multiple sensory modalities, such as vision and proprioception, is crucial for accurate end-effector tracking and control. Researchers have proposed a biologically inspired model for robot end-effector tracking using predictive multisensory integration.

This model focuses on learning visual feature descriptors without relying on visual markers, forward kinematics, or pre-defined visual feature descriptors. Instead, it uses a clustering analysis approach to learn the visual feature descriptors and then employs prediction to better integrate proprioception and vision.

The mathematical representation of this model can be expressed as follows:

x_t = f(x_t-1, u_t-1) + w_t
y_t = h(x_t) + v_t

Where:
– x_t is the state of the system at time t
– u_t is the control input at time t
– y_t is the observation at time t
– f(·) and h(·) are the state transition and observation functions, respectively
– w_t and v_t are the process and observation noise, respectively

By using this predictive multisensory integration approach, the robot can learn and adapt its end-effector tracking without relying on pre-defined visual features or markers, enabling more robust and versatile performance in real-world scenarios.

Conclusion

In this comprehensive guide, we have explored the technical specifications, modeling, control, and human-robot interaction aspects of robot end effectors. From the mathematical representations of human motor control models to the admittance control of rehabilitation robots and the integration of multisensory data, this guide provides a wealth of technical details and insights for science students and robotics enthusiasts.

By understanding the underlying principles and state-of-the-art advancements in robot end effector technology, you can better design, control, and integrate these crucial components into your robotic systems, enabling them to interact with their environment and perform tasks with increased precision, adaptability, and safety.

References

Adaptivity of End Effector Motor Control Under Different Sensory Conditions for Robotics Applications. Frontiers in Robotics and AI. Link
Quantitative Assessment of Motor Function by an End-Effector Upper Limb Rehabilitation Robot Based on Admittance Control. Applied Sciences. Link
Towards Active Physical Human-Robot Interaction: Quantifying the Human State During Interactions. HAL. Link
Robot End Effector Tracking Using Predictive Multisensory Integration. Frontiers in Neurorobotics. Link

The Profound Impact of Ozone Layer Depletion: A Comprehensive Exploration

June 18, 2024July 31, 2020 by Dr. Subrata Jana

The ozone layer, a crucial component of the Earth’s atmosphere, plays a vital role in shielding us from the sun’s harmful ultraviolet (UV) radiation. However, the depletion of this protective layer has far-reaching consequences that extend beyond the immediate effects on human health. This comprehensive blog post delves into the measurable and quantifiable impacts of ozone layer depletion on human health, the environment, and biogeochemical cycles, providing a detailed and technical exploration for science students.

Human Health Implications

Ozone layer depletion leads to an increase in UVB radiation reaching the Earth’s surface, which can have severe consequences for human health. According to the Atmospheric and Health Effects Framework model used by the EPA, this increased UVB exposure can:

Non-Melanoma Skin Cancer: UVB radiation is a known carcinogen and a major contributor to the development of non-melanoma skin cancers, such as basal cell carcinoma and squamous cell carcinoma. Studies have shown a direct correlation between increased UVB exposure and the incidence of these skin cancers.
Malignant Melanoma: UVB radiation also plays a significant role in the development of malignant melanoma, the most serious form of skin cancer. The International Agency for Research on Cancer (IARC) has classified UVB radiation as a Group 1 carcinogen, meaning it is a proven cause of human cancer.
Cataracts: Exposure to UVB radiation has been linked to the development of cataracts, a leading cause of vision impairment and blindness worldwide. The World Health Organization (WHO) estimates that a 1% decrease in ozone levels could result in an additional 1.6 million cataract cases globally.

To quantify the health benefits of stronger ozone layer protection, the EPA’s Atmospheric and Health Effects Framework model estimates that the Montreal Protocol has prevented millions of skin cancer cases and eye cataracts worldwide.

Plant Responses to Increased UVB Radiation

The effects of ozone layer depletion on plants are multifaceted and can have significant implications for ecosystems and biogeochemical cycles. UVB radiation affects the physiological and developmental processes of plants in the following ways:

Direct Effects: UVB radiation can directly impact plant growth, development, and productivity. It can cause damage to DNA, proteins, and cellular structures, leading to reduced photosynthesis, altered plant morphology, and decreased biomass production.
Indirect Effects: UVB radiation can also induce indirect changes in plants, such as alterations in nutrient distribution, developmental phases, and secondary metabolism. These changes can affect plant competitive balance, herbivory, and susceptibility to plant diseases, with cascading effects on the entire ecosystem.

To quantify these effects, researchers have conducted numerous experiments using controlled UV radiation levels. For example, a study published in the Journal of Photochemistry and Photobiology B: Biology found that a 10% increase in UVB radiation can lead to a 3-5% reduction in plant biomass production.

Impacts on Marine Ecosystems

Ozone layer depletion and the resulting increase in UVB radiation also have significant implications for marine ecosystems, particularly for phytoplankton, the foundation of aquatic food webs.

Phytoplankton Survival: Exposure to solar UVB radiation has been shown to reduce the survival rates of phytoplankton. A study published in the journal Marine Biology found that a 10% increase in UVB radiation can lead to a 5-10% decrease in phytoplankton biomass.
Trophic Implications: Reductions in phytoplankton populations can have cascading effects on the entire marine food chain, as these microscopic organisms are the primary producers that support higher trophic levels, such as zooplankton, fish, and marine mammals.

To quantify the impact on marine ecosystems, researchers have developed models that integrate the effects of UVB radiation on phytoplankton and higher trophic levels. For instance, the Biogeochemical Elemental Cycling (BEC) model, used in the Coupled Model Intercomparison Project (CMIP), estimates that a 1% decrease in ozone levels could result in a 0.5-1% reduction in global primary productivity in the oceans.

UVB Radiation and Ozone Layer Depletion

The relationship between ozone layer depletion and increased UVB radiation at the Earth’s surface is well-established. Reduced ozone levels mean less protection from the sun’s harmful rays, leading to higher UVB exposure.

Antarctic Ozone Hole: Studies have shown that in the Antarctic region, the amount of UVB radiation measured at the surface can double during the annual ozone hole event. This dramatic increase in UVB exposure has significant implications for the local ecosystem and human health.
Quantifying UVB Increases: Satellite data from the Total Ozone Mapping Spectrometer (TOMS) has been used to estimate the changes in surface UVB radiation due to ozone depletion. These estimates indicate that a 1% decrease in ozone levels can result in a 2-3% increase in erythemal UVB radiation, which is the type of UVB radiation that causes sunburn and skin damage.

Biogeochemical Cycle Alterations

Ozone layer depletion and the resulting increase in UVB radiation can also have far-reaching consequences for terrestrial and aquatic biogeochemical cycles, affecting both sources and sinks of greenhouse gases.

Terrestrial Biogeochemistry: UVB radiation can alter the decomposition rates of organic matter, the cycling of nutrients, and the production and consumption of greenhouse gases, such as carbon dioxide (CO2) and methane (CH4), in terrestrial ecosystems.
Aquatic Biogeochemistry: In aquatic environments, increased UVB radiation can affect the photochemical and biological processes that govern the cycling of carbon, nitrogen, and other essential elements, with potential impacts on the sequestration and release of greenhouse gases.

To quantify these biogeochemical cycle alterations, researchers have developed models that integrate the effects of UVB radiation on various ecosystem processes. For example, the Terrestrial Ecosystem Model (TEM) estimates that a 10% increase in UVB radiation could lead to a 2-5% change in the net ecosystem exchange of CO2 between the land and the atmosphere.

Aerosols, Pollutants, and Ozone Depletion

The relationship between ozone layer depletion and surface UVB radiation is further complicated by the presence of aerosols and pollutants in the atmosphere. These atmospheric constituents can interact with and modify the effects of UVB radiation.

Satellite Estimates vs. Ground Measurements: Satellite estimates of surface UVB radiation, such as those from the TOMS dataset, have been compared to ground-based measurements. The estimates are generally higher than the ground-based measurements, with differences ranging from 0% at clean sites to 40% at more polluted sites. This suggests that aerosols and pollutants near the ground can significantly influence the amount of UVB radiation reaching the surface.
Aerosol and Pollutant Effects: Aerosols and pollutants can scatter, absorb, or reflect UVB radiation, thereby altering the amount of radiation that reaches the Earth’s surface. The specific effects depend on the type, concentration, and optical properties of the atmospheric constituents.

To better understand these interactions, researchers are developing more sophisticated models that incorporate the effects of aerosols and pollutants on UVB radiation transfer and the subsequent impacts on human health, ecosystems, and biogeochemical cycles.

Hydrofluorocarbons (HFCs) and Ozone Depletion

Surprisingly, a class of widely used chemical coolants known as hydrofluorocarbons (HFCs) has been found to contribute to ozone depletion, albeit in a small but measurable way.

Indirect Ozone Depletion: A recent study by NASA found that HFC emissions can indirectly contribute to ozone depletion by causing increased warming of the stratosphere. This warming speeds up the chemical reactions that destroy ozone molecules, and it also decreases ozone levels in the tropics by accelerating the upward movement of ozone-poor air.
Quantifying HFC Impacts: The study focused on the five types of HFCs expected to contribute the most to global warming in 2050. The researchers found that these HFCs could indirectly account for up to 0.035 parts per million of ozone depletion, a small but significant amount that counters the previous assumption that HFCs were entirely benign to the ozone layer.

This unexpected finding highlights the complex and interconnected nature of atmospheric processes, underscoring the importance of continued research and monitoring to fully understand the impacts of human-made chemicals on the ozone layer and the Earth’s climate system.

References:
– Ozone Day: CAMS data helps protect life on Earth
– Health and Environmental Effects of Ozone Layer Depletion
– Executive Summary of the 2002 Assessment of Ozone Depletion
– NASA Study Shows That Common Coolants Contribute to Ozone Depletion