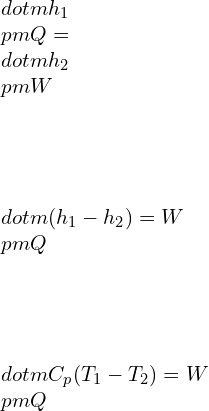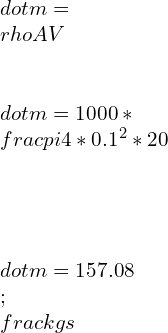Content
- Thermal diffusivity definition
- Unit of Thermal diffusivity
- Thermal diffusivity formula
- Thermal diffusivity of water
- Thermal diffusivity of air
- Thermal diffusion
- Thermal diffusivity of aluminium
- Flash method Thermal diffusivity
- How to measure Thermal diffusivity
- Thermal conductivity and thermal diffusivity
- Thermal diffusivity measurement techniques
- Thermal diffusivity of asphalt
- Thermal diffusivity of rubber
- Thermal diffusivity values
- Thermal diffusivity symbol
- The highest Thermal diffusivity is of
- Thermal diffusivity of sand
- Thermal diffusivity heat transfer
- The Thermal diffusivities for gases are generally
- Thermal diffusion coefficient
- Thermal diffusion meaning
- Glass Thermal diffusivity
- stainless steel Thermal diffusivity
- Thermal diffusion ratio
Thermal diffusivity definition
Thermal diffusivity is defined as the ratio of conducted heat to heat stored in material per unit volume.
Unit of Thermal diffusivity
The unit of thermal diffusivity is given as m2/s
Thermal diffusivity formula
The equation of thermal diffusivity is given by,
α = k/ρ
Where,
α is thermal diffusivity,
k is thermal conductivity (w/mK)
? is the density of the material (kg / m3)
Cp is the specific heat (J/ kg k)
Thermal diffusivity of water
The thermal diffusivity of water changes with temperature and pressure. If we consider atmospheric pressure condition, then the thermal conductivity values with temperature are given as below table.
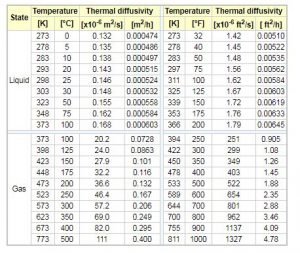
Thermal diffusivity of air
The thermal diffusivity of air with temperature change is shown in the above table. Generally , the thermal diffusivity of gas is more than liquid in practice. we will study is more in next topic.
Thermal diffusion
Thermal diffusion of substance is the relative motion of the molecules due to temperature gradient.
Thermal diffusivity of aluminium
Thermal diffusivity of aluminium material is given as 9.7 * 10-5 m2/s
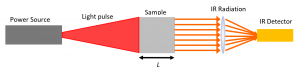
Flash method Thermal diffusivity
The flash method is used to determine the thermal diffusivity of the material. The short duration radiant energy pulse is passed through the sample. The laser or light flash lamp source is used for radiant energy. The piece will absorb the emitted energy. The process is repeated for the sample. Due to this emitted radiation, there is a temperature increase of the material sample. The infrared temperature detector records this increase in temperature.
The duration of the measured signal is calculated. The thermal diffusivity will be found from the following equation.
α = 0.1388/l2(t2)
=
Where L is the sample thickness,
t/2 is the half time,
we can find thermal diffusivity, specific heat, and density using the flash method.
The schematic diagram of the flash method is shown in the figure below
How to measure Thermal diffusivity
The thermal diffusivity can be measured using the flash method as discussed above. in this method, the short energy pulse is radiated one end, and temperature rise is calculated on the other end.
Thermal conductivity and thermal diffusivity
To differentiate between thermal conductivity and thermal diffusivity, consider two materials having the same thermal conductivity but with different thermal diffusivity. Both will permit the same rate of heat flow in the steady-state condition. At the start of the heat transfer process, the material with higher thermal diffusivity will reach a steady-state first compared to other material since it retains less heat energy. Heat energy penetrates fast through this material, but after getting a steady-state, the rate of heat flow will be the same. Also, remember that the material having less thermal diffusivity takes more time to reach the steady state.
Thermal diffusivity measurement techniques
There are mainly three types of thermal diffusivity measurement techniques.
- Flash method
- Thermal wave interferometry
- Thermographic method
Thermal diffusivity of asphalt
The thermal diffusivity of the asphalt (Ah-70) is 0.123 mm2/s,
Asphalt (Ah-90) 0.128 mm2/s
Thermal diffusivity of rubber
The thermal diffusivity of the rubber material is in the range of 0.089-0.13 mm2/s
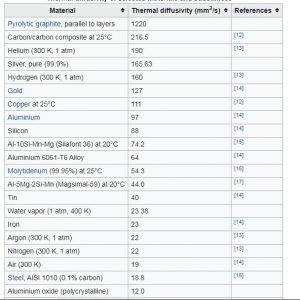
Thermal diffusivity values
Thermal diffusivity values for various materials are given in the table below. The values are changes with properties like temperature. These values are given for standard temperature and pressure.
Thermal diffusivity symbol
The symbol of thermal diffusivity is α
The highest Thermal diffusivity is of
The highest thermal diffusivity is of pure silver 165.63 mm2 / s
Thermal diffusivity of sand
Thermal diffusivity of dry sand varied from 0.6 * 10-7 to 7.0 * 10-7 m2/s.
Thermal diffusivity heat transfer
There are three modes of heat transfer conduction, convection and radiation. Heat conduction is dependent on main two properties. One is thermal conductivity and thermal diffusivity. Thermal conductivity is well-known property, but thermal diffusivity is not well known. It defines the rate of heat transfer through a given medium.
The rate of heat transfer is faster is the thermal diffusivity is higher. Thermal diffusivity is balancing between the medium of heat transfer and heat storage.
The Thermal diffusivities for gases are generally
The thermal diffusivities of gases substance are found more than liquid substance
Thermal diffusion coefficient
It is one of physical parameter which describes the dependency of mass diffusion flow of the mixture. In other words, the thermal diffusion coefficient is the ratio of a temperature gradient to the absolute temperature.
Thermal diffusion meaning
Thermal diffusion of substance is the relative motion of the molecules due to temperature gradient.
Glass Thermal diffusivity
The thermal diffusivity of glass is 0.34 * 10-6 m2/s at normal atmospheric condition.
Stainless steel Thermal diffusivity
The thermal diffusivity of stainless steel at 100 °C is 4.55 *10-6 m2/s
Thermal diffusion ratio
The thermal diffusion ratio is the ratio of the thermal diffusion coefficient to the concentration coefficient.
FAQs
Thermal diffusivity of gas vs liquid
The thermal diffusivities of gases substance are found more than liquid substance
Which material has the highest Thermal diffusivity
The most increased thermal diffusivity is of pure silver 165.63 mm2 / s
Application of Thermal diffusivity
The conduction heat transfer in any apparatus requires the study of thermal diffusivity. The industries are using the analysis of thermal diffusivity to optimize the heat transfer rate.
If we take a particular example, then insulation is one example. In insulation, the thermal diffusivity of the material is minimum so that it can resist maximum heat flow.
We are using computers, laptops and other electronic gadgets. Do you know what the method to extract heat from devices is? Yes, it’s Heat sinks.
Heat sink requires higher thermal diffusivity to transfer faster heat from any gadgets.
An increase in heat transfer in any electronics degrades its performance. The higher thermal diffusivity material should be used to improve its performance in that case.
Thermal diffusivity of concrete
The thermal diffusivity of the concrete is 0.75 *10 -6 m2/s
What is the physical significance of thermal diffusivity?
Thermal diffusivity can be defined as the ratio of the thermal conductivity of the substance to the heat storage capacity of the substance.
The ratio defines the generated heat gets diffused out at a specific rate. The higher value of thermal diffusivity indicates that the time required for heat diffusion is less. The study of the equation of thermal diffusivity can be possible by the higher value of thermal conductivity or the lower value of heat capacity.
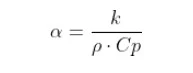
Thermal diffusivity is helpful for more intransient heat transfers. In steady-state heat transfer, the thermal conductivity is enough to study.
Why is the thermal diffusivity of gas greater than liquid even though the thermal conductivity of the liquid is greater than gases?
Thermal diffusivity means the ability of a material to transfer heat and store the heat at an unsteady state. A faster heat transfer can be possible if the thermal diffusivity is higher. The lower thermal diffusivity of material means the storage of heat in it.
Gas possesses low volumetric heat capacity because of low density. Due to low volumetric heat capacity, the value of thermal diffusivity is high.
Liquid possesses a high heat capacity compare to gas; hence thermal diffusivity is lower in the liquid.
What is the order of thermal diffusivity for solid, liquid, and gas?
The order of thermal diffusivity in solid, liquid and gas as shown below,
Gas > Liquid > Solid
What is the difference between momentum diffusion and thermal diffusion?
Momentum diffusion
It can be considered the kinematic viscosity of the fluid, i.e. the ability of the fluid to flow the momentum. Momentum diffusion is occurred by shear stress in a fluid. Shear stress causes a random and any direction movement of molecules.
Thermal diffusion
It can be defined as thermal conductivity divided by the multiplication of density and specific heat capacity (when the pressure is constant). It measures the heat transfer rate for a given material from the hot side to the cool side. It is predictive analogous to whether a given material is “cool to the touch.”
How is the Prandtl number related to kinematic viscosity and thermal diffusivity?
The Prandtl Number is dimensionless. It can be given as the ratio of momentum diffusivity (it is kinematic viscosity as explained above) to thermal diffusivity.
It can be formulated in equation as,
Pr = v/α
Pr = Prandtl number
V= momentum diffusivity ( m2/s )
α = Thermal diffusivity ( m2/ s )
MCQs
Thermal diffusivity is the _________
(a) Dimensionless parameter (b) Function of heat (c) Physical property of the material
(d) All of the above
Thermal diffusivity of a material is __________________?
(a) directly proportional with thermal conductivity (k)
(b) inversely proportional with the density of a material
(c) inversely proportional with specific heat
(d) all of the above
(e) none of the above
Find the wrong statement: Specific heat of a material ______________.
(a) Constant for a material (b) Heat capacity per unit mass
(c) Extrinsic property (d) Has units as J/kg-K.
What is a unit of thermal diffusivity?
(a) m/h
(b) m²/h
(c) m/hk
(d) m²/hk
Thermal diffusivity of solid is less than liquid.
(a) True
(b) False
Thermal diffusivity is higher in…….
(a) Rubber
(b) Lead
(c) Iron
(d) Concrete
Thermal diffusivity is lower in……
(a) Rubber
(b) Lead
(c) Aluminum
(d) Iron
Find more articles to related topic click here
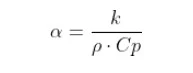
![Rendered by QuickLaTeX.com \\sigma x'=\\frac{\\left ( \\sigma x+\\sigma y \\right )}{2}+\\frac{1}{R}[\\left ( \\frac{\\sigma x-\\sigma y}{2} \\right )^{2}+\\sigma xy^{2}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-101a7fbba4f959bb0d8ed8e3b7294114_l3.png)






![Rendered by QuickLaTeX.com \\gamma xy=\\frac{1}{(1+\\varepsilon x)+(1+\\varepsilon y)}[2\\left ( nx1nx2\\varepsilon 1+ny1ny2\\varepsilon 2+nz1nz2\\varepsilon 3 \\right )+\\left ( nx1nx2+ny1+ny2+nz1+nz3 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-cf0ff2b75b9b650d50f0eef50e392519_l3.png)

![Rendered by QuickLaTeX.com \\gamma xy= [\\lambda \\Delta\\left ( nx1nx2\\varepsilon 1+ny1ny2\\varepsilon 2+nz1nz2\\varepsilon 3 \\right )+\\left ( nx1nx2+ny1+ny2+nz1+nz3 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-dab83b91fc5915165b4a1f6465aceeb9_l3.png)

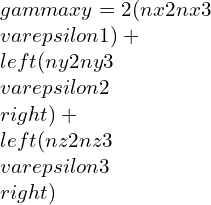
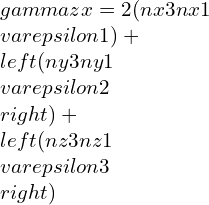

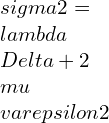
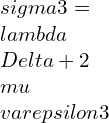
![Rendered by QuickLaTeX.com \\varepsilon 1=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma 1-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma 2+\\sigma 3 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-eb8240f97d2550c83d5b61674ea15b8b_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon 2=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma 2-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma 3+\\sigma 1 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-5916a79321f0d60e68e015fef9565945_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon 1=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma 3-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma 1+\\sigma 2 \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-a7605cc38352f88f24ecedc6fe5562de_l3.png)
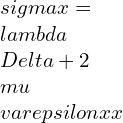
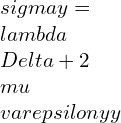

![Rendered by QuickLaTeX.com \\varepsilon xx=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma x-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma y+\\sigma z \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ba8c810228c7f208ab4b329c1ec8ba53_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon yy=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma y-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma x+\\sigma z \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-283d086fdb3111924fe0a590906dc759_l3.png)
![Rendered by QuickLaTeX.com \\varepsilon zz=\\frac{\\lambda +\\mu }{\\mu \\left ( 3\\lambda +2\\mu \\right )}[\\sigma z-\\frac{\\lambda }{2\\left ( \\lambda +\\mu \\right )}\\left ( \\sigma x+\\sigma y \\right )]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-410e232a635a25e92b2370459cbcdad0_l3.png)

![Rendered by QuickLaTeX.com \\delta =\\frac{64WR^{3}nsec\\alpha }{d^{4}}[\\frac{cos^{2}\\alpha }{N}+\\frac{2sin^{2}\\alpha }{E}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-e7d33fd56d11bedb00c79154eebdac87_l3.png)

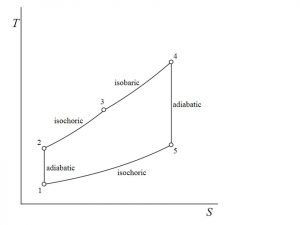
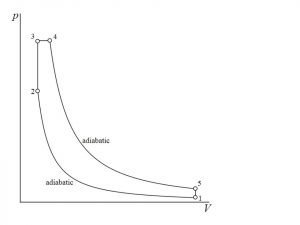
![Rendered by QuickLaTeX.com \\eta_{dual}=1-\\frac{1}{r_k^{\\gamma -1}}[\\frac{r_pr_c^\\gamma -1}{(r_p-1)+r_p\\gamma (r_c-1)}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ef5d62cb8110d7b8f13b61f35836bb06_l3.png)

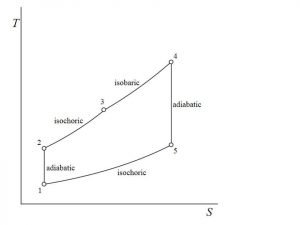
![Rendered by QuickLaTeX.com \\\\\\eta=1-\\frac{(T_5-T_1)}{([T_3-T_2 ]+\\gamma[T_4-T_3])}\\\\\\\\ \\eta_{dual}=1-\\frac{1}{r_k^{\\gamma -1}}[\\frac{r_pr_c^\\gamma -1}{(r_p-1)+r_p\\gamma (r_c-1)}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-8d7a6e6fd77001105b5968b92751f278_l3.png)
![Rendered by QuickLaTeX.com M.E.P=\\frac{(P_1 [\\gamma r_p r_k^\\gamma (r_c-1)+r_k^\\gamma (r_p-1)-r_k (r_p r_c^\\gamma-1) ] )}{(\\gamma-1)(r_k-1) }](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-b84ee279a3d25c3e77b699126299c702_l3.png)



![Rendered by QuickLaTeX.com \\\\Q_v=C_v [T_3-T_2 ]=0.718*[1199-671]=379kJ/kg\\\\\\\\ (2/3)*Q=Q_v\\\\\\\\ Q=(3/2)*379=568.5 kJ/kg\\\\\\\\ C_p [T_4-T_3 ]=Q/3\\\\\\\\ 1.005*[T_4-1199]=568.5/3\\\\\\\\ T_4=1387.55 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-16101adc0e9d29571aa2ae5394d2b62b_l3.png)

![Rendered by QuickLaTeX.com \\\\r_c=[T_4/T_3 ]=[1873/1433]=1.307\\\\\\\\ Also \\;\\\\\\\\ r_c=[V_4/V_3] =1.307\\\\\\\\ V_4=1.307*0.004=5.228*10^{-3} m^3](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-b809892b3aac2d862e3a5f4e08ca9735_l3.png)
![Rendered by QuickLaTeX.com \\\\T_5/T_4 =[V_4/V_5] ^{\\gamma-1}\\\\\\\\ (T_5/1873)=[\\frac{(5.228*10^{-3})}{0.07}]^{1.4-1}\\\\\\\\ T_5=663.48 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-3c2788b7142d2658ebd2be9ada56a46a_l3.png)
![Rendered by QuickLaTeX.com \\\\Q_s=C_v [T_3-T_2 ]+C_p [T_4-T_3 ]\\\\\\\\ Q_s=0.717*(1433-942.6)+1.005*(1873-1433)\\\\\\\\ Q_s=793.81 kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-e98662763e1036e6adb2d3e4c2f5db76_l3.png)





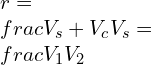


![Rendered by QuickLaTeX.com \\\\\\eta=1-\\frac{[T_4-T_1]}{[T_3-T_2]}\\\\\\\\ \\frac{T_2}{T_1}=\\frac{T_3}{T_4}\\\\\\\\ \\frac{T_4}{T_1}=\\frac{T_3}{T_2}\\\\\\\\ \\eta=1-\\frac{1}{r^{\\gamma-1}}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f49c7bd3e52c0f607a4e2c504e1ab46b_l3.png)

![Rendered by QuickLaTeX.com \\\\1000=0.717*[473-1188+T_3-T_4]\\\\\\\\ 1000=0.717*[473-1188+2.512 T_4-T_4]\\\\\\\\ T_4=1395 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-7b3a245ad98e31383d6f4d9583e34a18_l3.png)
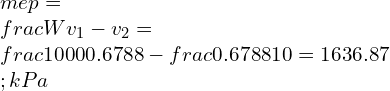
![Rendered by QuickLaTeX.com \\\\\\frac{\\mathrm{d} C_v}{C_v}=0.02\\\\\\\\ \\eta=1-\\frac{1}{r^{\\gamma -1}}=1-\\frac{1}{6^{1.4 -1}}=0.511\\\\\\\\ \\gamma -1=\\frac{R}{C_v}\\\\\\\\ \\eta=1-[\\frac{1}{r}]^\\frac{R}{C_v}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-757291f702fb1983830f344901562518_l3.png)
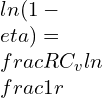
![Rendered by QuickLaTeX.com \\\\\\frac{d\\eta}{1-\\eta}=\\frac{-R}{C_v^2}*dC_v*ln[1/r]\\\\\\\\ \\frac{d\\eta}{1-\\eta}=\\frac{-R}{C_v}*\\frac{dC_v}{C_v}*ln[1/r]\\\\\\\\ \\frac{d\\eta}{\\eta}=\\frac{1-\\eta}{\\eta}*\\frac{-R}{C_v}*\\frac{dC_v}{C_v}*ln[1/r]\\\\\\\\ \\frac{d\\eta}{\\eta}=\\frac{1-0.511}{0.511}*\\frac{-0.287}{0.718}*0.02*ln[1/6]\\\\\\\\ \\frac{d\\eta}{\\eta}=-0.0136\\\\\\\\ \\frac{d\\eta}{\\eta}*100=-0.0136*100=-1.36\\%](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ef306304ee4e226f05089530564c7534_l3.png)

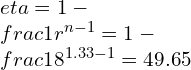


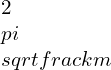




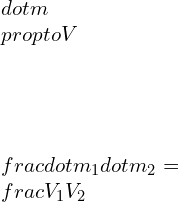
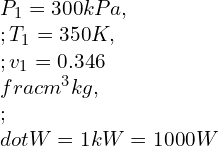
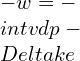
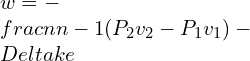
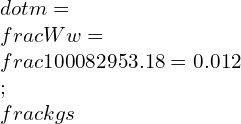
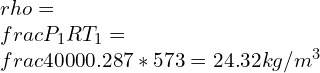
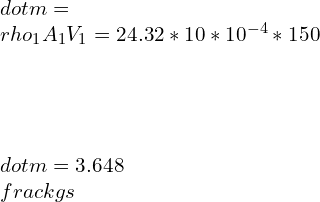
![Rendered by QuickLaTeX.com \\\\\\dot{m}h_1+Q=\\dot{m}h_2+W\\\\ \\\\\\dot{m}[h_1-h_2]=W-Q\\\\ \\\\\\dot{m}C_p[T_1-T_2]=W-Q\\\\ \\\\\\dot{m}=\\frac{W-Q}{C_p[T_1-T_2]}=\\frac{4600+300}{1100-400}=7\\;\\frac{kg}{s}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ab801810045c79c44023956f8f7184db_l3.png)


![Rendered by QuickLaTeX.com \\\\P=\\dot{m}[h_1-h_2]\\\\ \\\\\\dot{m}=\\frac{P}{h_1-h_2}\\\\ \\\\\\dot{m}=\\frac{P}{C_p[T_1-T_2]}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f9d3656cc8e9eecbd79512180f849452_l3.png)