Wave

In this article, we will discuss the effect of refraction on wavelength while propagating from one medium to another, with detailed facts.

The frequency of the wave does not vary on refraction of the wave, hence, the wavelength of the wave is directly proportional to its speed. As the speed of the wave varies on traversing from mediums, the wavelength also shifts accordingly.

Does Refraction Affect Wavelength?

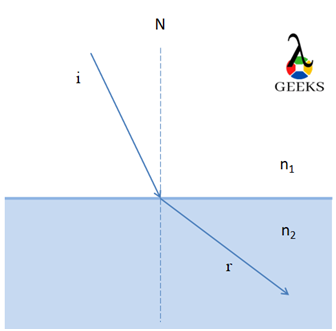
The refraction occurs when the ray of light travels from medium to another.

The velocity of the wave increases while traversing from the rarer mediums and decreases in denser mediums that determines the angle of refraction. The wavelength of the wave is relative to the velocity and varies parallelly.

We know that, the speed of the light c=λf. For any wave, propagating from two different mediums, moving with speed ‘v’ is directly proportional to the wavelength, as the frequency of the wave remains the same after refraction.

The velocity of the wave in the medium is directly dependent on the refractive index of the medium it is traversing through.

n₁/n₂ = v₂/v₁

v₂/v₁=λ_2f/λ_1f

As the frequency remains constant even after refraction,

v₂/v₁=λ₂/λ₁

Hence,

n₁/n₂=λ₂/λ₁

The refraction of the wave depends upon the wavelength and the wavelength is inversely proportional to the refractive index of the medium.

Read more on Types Of Refraction: Comparative Analysis.

How does Refraction Affect Wavelength?

The refraction may increase or decrease the wavelength of the light or sound propagating in the medium having higher density than the air.

When a wave travels in the denser medium the speed of the wave decreases and hence the wavelength decreases. The wavelength increases if the speed of the wave increases while traveling in a rarer medium.

Consider a wave propagating from rarer medium to denser medium and back to the rarer medium as shown in the below figure.

The velocity of the wave in the rarer medium is more and hence the wavelength of the wave is increased. On passing to the denser medium having a slightly greater refractive index, the speed of the wave and the wavelength reduces. On entering back to the rarer medium, the wavelength and speed of the wave increase.

Read more on What is the wavelength of photon: How to Find, Several Insights And Facts.

How does Index of Refraction Affect Wavelength?

The denser the medium, the velocity of the wave will decrease and hence the wavelength reduces.

The index of refraction is greater for the denser medium than the rarer because the speed and in proportionate the wavelength of the wave is reduced while traveling through the denser medium.

The refractive index of the medium is given as the velocities of the wave propagating from two different mediums. Suppose the light travels from medium 1 to medium 2, the refractive index of the medium is given as

n₁₂=n₁/n₂=λ₂/λ₁

Where n₁ is a refractive index of medium 1

n₂ is a refractive index of medium 2

v₁ is a velocity of light in medium 1

v₂ is a velocity of light in medium 2

The speed of the wave is equal to the product of the wavelength and the frequency of the wave.

v=λ f

Let us take an example to clarify how does the wavelength of the wave depends upon the refractive index of the medium it is traveling through.

Read more on Refractive Index.

Example: Consider a wave of light propagating from air to water. If the frequency of the wave is equal to 6* 10¹⁶ /sec. Calculate the change in the wavelength of the light.

Given: f=6* 10¹⁶ /sec

Refractive index of air n₁=1

Refractive index of water n₂=1.33

n=c/v

n=c/λf

λ=c/nf

This shows that the wavelength is inversely proportional to the refractive index of the medium.

Wavelength of the light in air was

λ₁=c/n_1f

λ₁=3* 10⁸ / 1* 6 * 10¹⁶

λ₁=5*10⁷=500*10^-9=500nm

After refraction, the wavelength of the light in water becomes

λ₂=c/n_2f

λ₂=3* 10⁸/ 1.33* 6* 10¹⁶

λ₂=3.75* 10^-7=375*10^-9=375nm

It is clearly indicating that as the refractive index of the medium increased, the wavelength of the light decreased.

This implies that the speed of the light decreases in the medium having a greater refractive index, and increases while traversing from the medium of higher refractive index to lower refractive index.

Why does Wavelength Affect Refraction?

The refraction basically depends upon the density of the medium, and the temperature and pressure gradient of the medium.

As the density of the medium varies, the wavelength differs, and the direction of the propagation of the wave changes. If the wavelength increases, the angle of refraction will be greater.

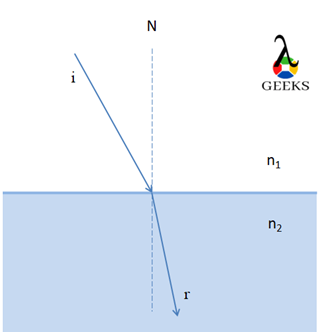
When a wave travels from a denser to a rarer medium, the speed of light and hence the wavelength increases, and the refractive angle produced on bending the ray of light will be greater.

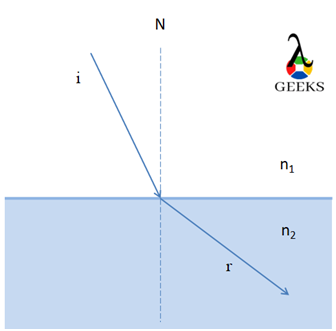
While a wave propagates from a rarer to a denser medium, the wavelength will decrease, and the refractive angle formed on bending the ray of light will be smaller.

Read more on How To Find Angular Acceleration From Angular Velocity: Problem And Examples.

Frequently Asked Questions

Why does the refractive index of glass is more than the air?

The refractive index is determined by the change in the speed of light while traversing from a given medium.

The speed of the light reduces to a greater extent in the glass compared to the speed of light in the air. Hence, the refractive index of a glass is more compared to air.

What will be the effect on the refraction if the frequency of the wave increased?

The frequency remains constant on refraction and is inversely correlated to the wavelength.

If the frequency increases then the speed of the wave will reduce, and the wave will divert towards the normal producing a small angle of refraction.

When does a ray of a light disperse after refraction?

If the white light traverses through the medium and emerges out at the same angle then the dispersion of light does not occur.

If all the components of the light emanating out from the medium at different angles then this phenomenon is called the dispersion of the light.

Why does the frequency of a light does not changes while propagating from higher density medium?

The speed of light decreases while traveling from the denser medium.

The frequency determines the propagation of light in time. As the speed reduces the wavelength will also shrink, thus the frequency remains constant.

Also Read:

• Frequency of a wave example
• How does a microwave vent work
• Types of sound waves
• Refraction of waves examples
• How are light waves produced
• Longitudinal wave example
• Sound wave equations
• Electromagnetic waves types
• How to calculate wave energy in ocean engineering
• How was the wave nature of light established

The wavelength of photons tells us about their energy. So in this article, we will look at what is the wavelength of photons and how to find it. Let us begin.

Photons travel through electromagnetic waves. As the photon is ultimately a part of the electromagnetic wave, its wavelength will be the same as the electromagnetic wave. If the energy and frequency of a photon are known, then from that, one can easily find the wavelength of the photon.

Before we get into the wavelength of a photon, let’s have a look at what a photon is.

Photon:

As the energy that is contained by photons is not divisible, they are often described as energy packets. Maxwell has described photons as electric fields which are traveling through space. Or, to put it another way, photon energy is stored in the form of an oscillating electric field that can oscillate at any frequency. Thus a quantum of electromagnetic radiation or energy is called a photon. 

Photons are particles that have neither a charge nor a mass. As a result, they are able to travel at the speed of light. The speed of the electric field can decide the speed of the photons in free space. The emission of photons is possible by means of the action of the charged particles and some other methods like radioactive decay.

What is the wavelength of photon?

The properties of photons are the same as those of electromagnetic waves. As a result, each photon is associated with its unique frequency and wavelength.

Photons travel in waves, as though each one is riding a roller coaster that only uses the same track repeatedly. The wavelength of a photon wave is the length of the wave, or more precisely, the distance between two consecutive points of the same phase of the wave.

Three different wavelengths are shown in the diagram below. Although photons do not have color, they will correspond to the light of that particular color.

How to find wavelength of a photon?

The length of an electric field wave, or a photon wave, is the wavelength of a photon.

To determine the wavelength of a photon, either its energy or frequency is used. As a result, if any of them are known, the wavelength of a photon can be found easily.

Let’s look at how to find wavelength of a photon using frequency and energy.

How to find wavelength of a photon with frequency?

The frequency and the wavelength of a photon are related to each other. 

The length of the photon wave gives the wavelength of the photon wave. While the number of photon wavelengths that propagates every second gives us the frequency of photon waves. As a result, if a photon’s wavelength is short, its frequency will be high, and its frequency will be low if its wavelength is long.

As one increases while the other decreases, we can say that they have an inverse relationship. Let us derive a mathematical equation that reflects the link between photon frequency and wavelength.

Several quantities such as wavelength, period, frequency, and so on can be used to describe a wave. As we know, the frequency of a photon wave determines the number of photon waves that propagate each second. As a result, the frequency of a photon wave can be calculated as follows:

……….(1)

Where f is the frequency of the photon wave, and T is the period of the photon wave, i.e., the time it takes for the photon wave to complete one cycle.

After one period, every wave point returns to the same value. This happens because in a wave during one period, one oscillation occurs, and each oscillation travels a distance of one wavelength in that time.

The distance traveled by any wave in a unit of time determines its speed. But as the wave is traveling with the speed of light, thus we denote it with the letter c, and it can be given by:

……….(2)

From equations (1) and (2), we can write:

c = ????f ……….(3)

Thus, the wavelength of the photon is given by:

……….(4)

Because the speed of light c is constant and has a value of 3 X 10⁸ m/s, we may deduce from the above equation that the wavelength of a photon is inversely proportional to its frequency.

How to calculate wavelength of a photon given energy?

The frequency of a photon relates to both its energy and wavelength. As a result, the photon’s wavelength is also connected to its energy.

The photon wave’s wavelength contains information about its energy. A shorter wavelength photon wave will have a higher frequency and consequently higher energy. Similarly, a photon wave with a longer wavelength will have a lower frequency and thus less energy.

Also, in this case, a longer wavelength corresponds to lower wave energy, whereas a shorter wavelength corresponds to higher wave energy. As a result, we can state that the wavelength of the photon wave and its energy are inversely proportional. In terms of an equation, let’s look at the relationship between energy and wavelength of the photon wave.

According to the great scientist Max Plank, light is composed of discrete packets of energy known as quanta of light, which are also known as photons. The energy of light can only have discrete values. Plank further said that energy is given by the product of photon frequency and a constant known as Plank’s constant. We can express it mathematically as follows:

E = hf ……….(5)

Where h = Plank’s constant (6.626 X 10^-34 J s)

When we compare equations (4) and (5), we get the following expression for energy:

……….(6)

Rearranging Plank’s equation, the wavelength of a photon in terms of energy is given by:

……….(7)

Thus, if the energy of a photon or light wave is known, the wavelength of the photon can be determined using Plank’s equation.

Some problems of finding the wavelength of the photon using frequency and energy:

Problem: What is the wavelength of a light wave with a frequency of 7 X 10¹⁴ Hz?

Given parameters:

Frequency of photon f =7 X 10¹⁴ Hz

Speed of light c = 3 X 10⁸ m/s

To Find:

Wavelength of photon ???? = ?

Solution:

???? = c / f

???? = 3 X 10⁸ /  7 X 10¹⁴

∴ ???? = 0.428 X 10^-6 m

∴ ???? = 428  nm

As a result, a photon with a frequency of 7 X 10¹⁴ Hz has a wavelength of 428 nm.

Problem: What wavelength will a photon have if its energy is4 X 10^-15 J?

Given parameters:

Energy of photon E = 4 X 10^-15 J

Plank’s constant h = 6.626 x 10^-34 Js

Speed of light c = 3 X 10⁸ m/s

To Find:

Wavelength of photon ???? = ?

Solution:

???? = hc/ E

???? = 6.626 X 10^-34 X   3 X 10⁸ /  4 X 10^-15

∴ ???? = 5 X 10^-11 m

∴ ???? = 500 nm

As a result, a photon with an energy of 4 X 10^-15 J has a wavelength of 500 nm.

Problem: If the energy of a photon is 2.19 × 10¹¹ ev, determine the wavelength of that photon.

Given parameters:

Energy of photon E = 2.19 × 10¹¹ ev

∴ E = 2.19 × 10¹¹ X 1.6 X 10-19 

∴ E = 3.05 × 10^-8 J =350 X 10^-10 J  

Plank’s constant h = 6.626 x 10^-34 Js

Speed of light c = 3 X 10⁸ m/s

To Find:

Wavelength of photon ???? = ?

Solution:

???? = hc/ E

???? = 6.626 X 10^-34 X   3 X 10⁸ /  350 X 10^-10

∴ ???? = 0.056 X 10^-16 m

As a result, a photon with an energy of 2.19 × 10¹¹ ev has a wavelength of 0.056 X 10^-16 m.

Also Read:

• Amplitude of a wave example
• How to harness mechanical energy in wave power generation
• Why is light considered both a wave and a particle in quantum mechanics
• How to find energy from wavelength
• Amplitude of a wave
• Wave interference examples
• How to find amplitude of transverse wave
• Electromagnetic waves types
• Why does light exhibit both wave and particle characteristics
• Effect of wavelength on refraction