Momentum

The principle of conservation of energy is a fundamental concept in physics that states that the total energy in an isolated system remains constant over time. Energy can take many forms, including kinetic energy, potential energy, thermal energy, and more. In mechanics, the principle of conservation of energy is often referred to as the principle of conservation of mechanical energy, which states that the sum of an object’s kinetic energy and potential energy remains constant if the system is only subject to conservative forces.

Understanding the Relationship between Momentum and Energy

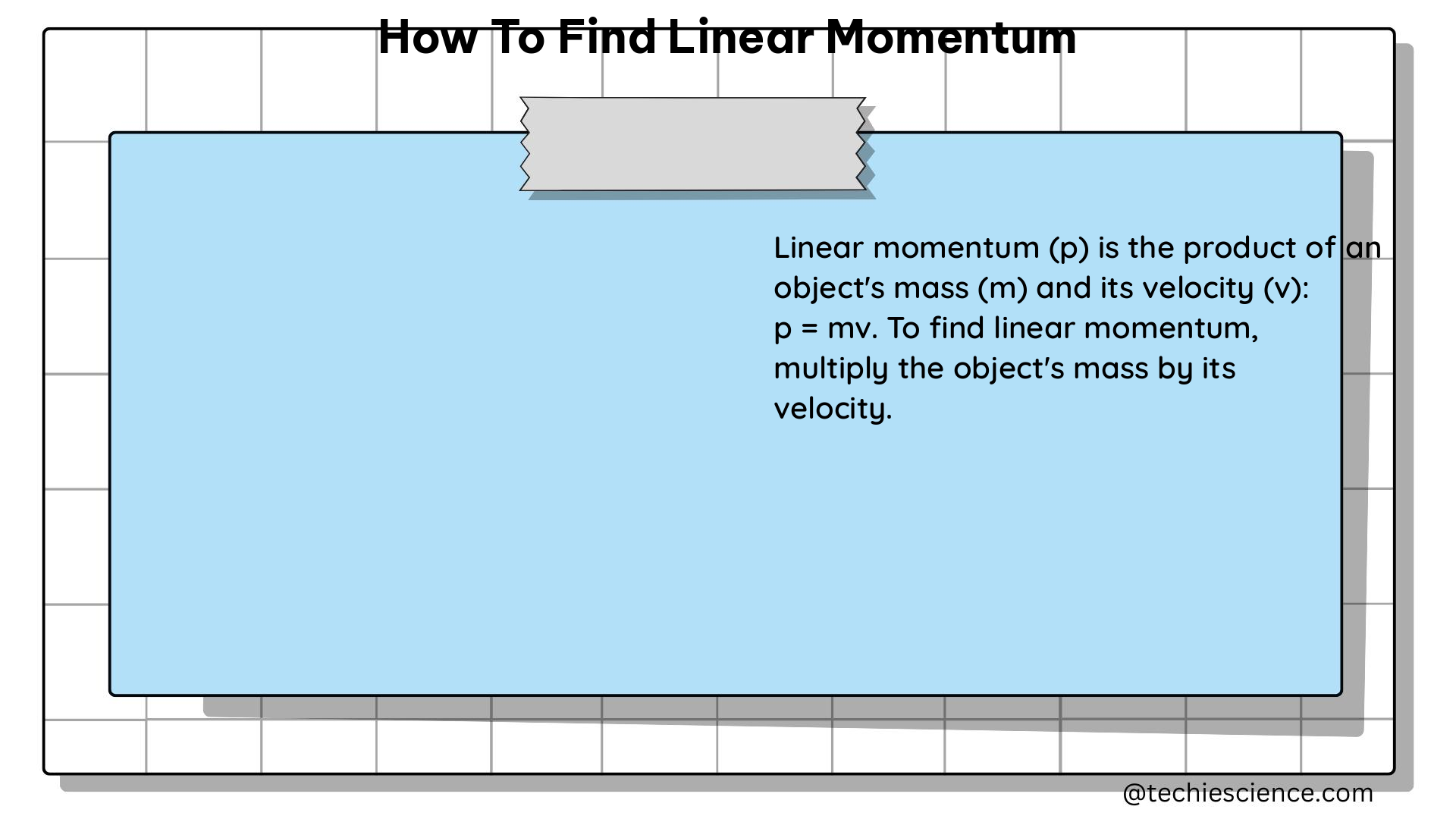
Momentum and energy are related but distinct physical quantities in classical mechanics. Momentum is a vector quantity that describes the motion of an object, while energy is a scalar quantity that describes the object’s ability to do work or cause change.

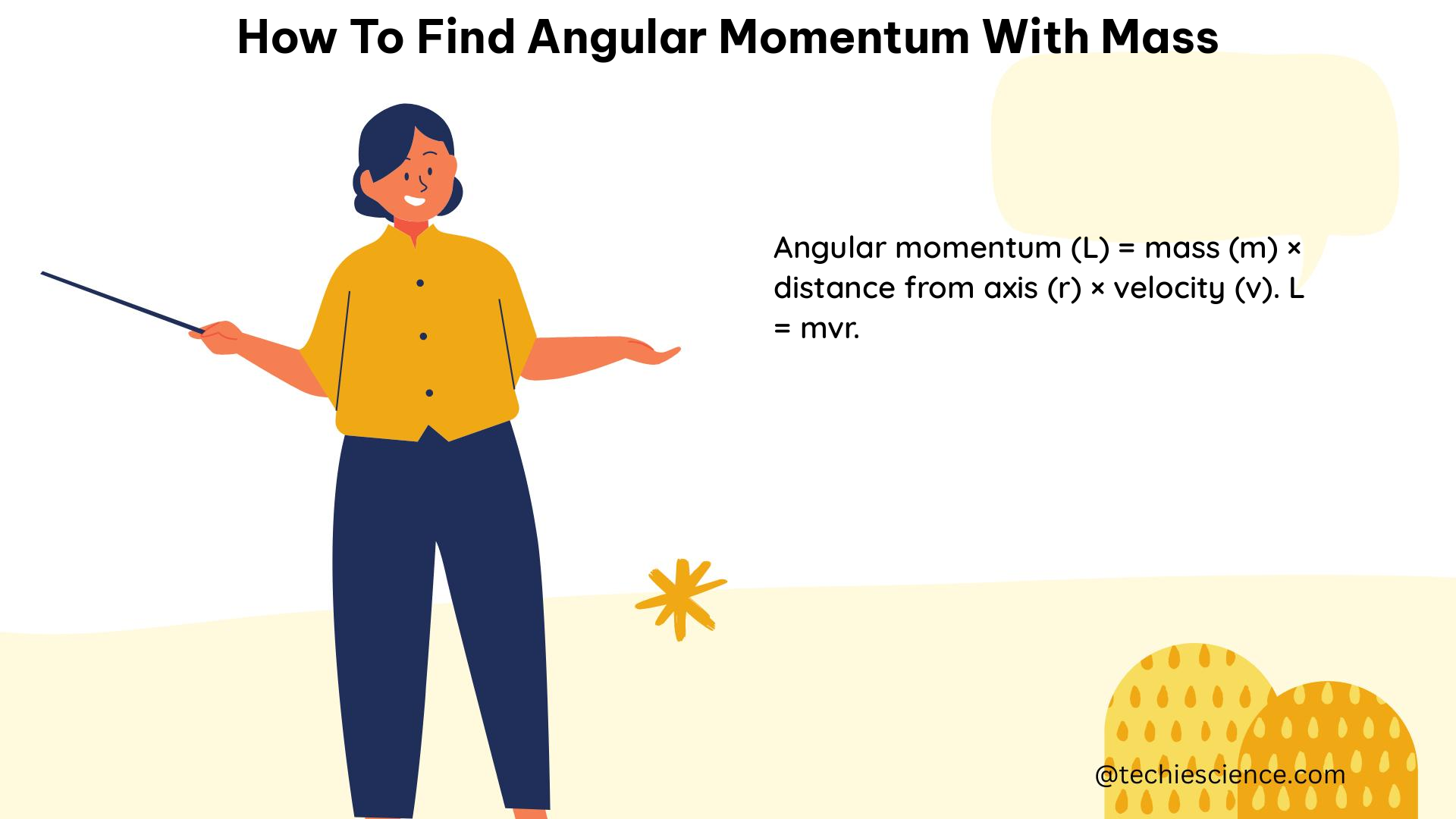
The relationship between momentum and energy can be expressed mathematically as:

E = (p^2) / (2m)

Where:
– E is the kinetic energy of the object
– p is the momentum of the object
– m is the mass of the object

This equation shows that the kinetic energy of an object is proportional to the square of its momentum, divided by its mass. This means that as an object’s momentum increases, its kinetic energy also increases, but not in a linear fashion.

Conservation of Momentum vs. Conservation of Energy

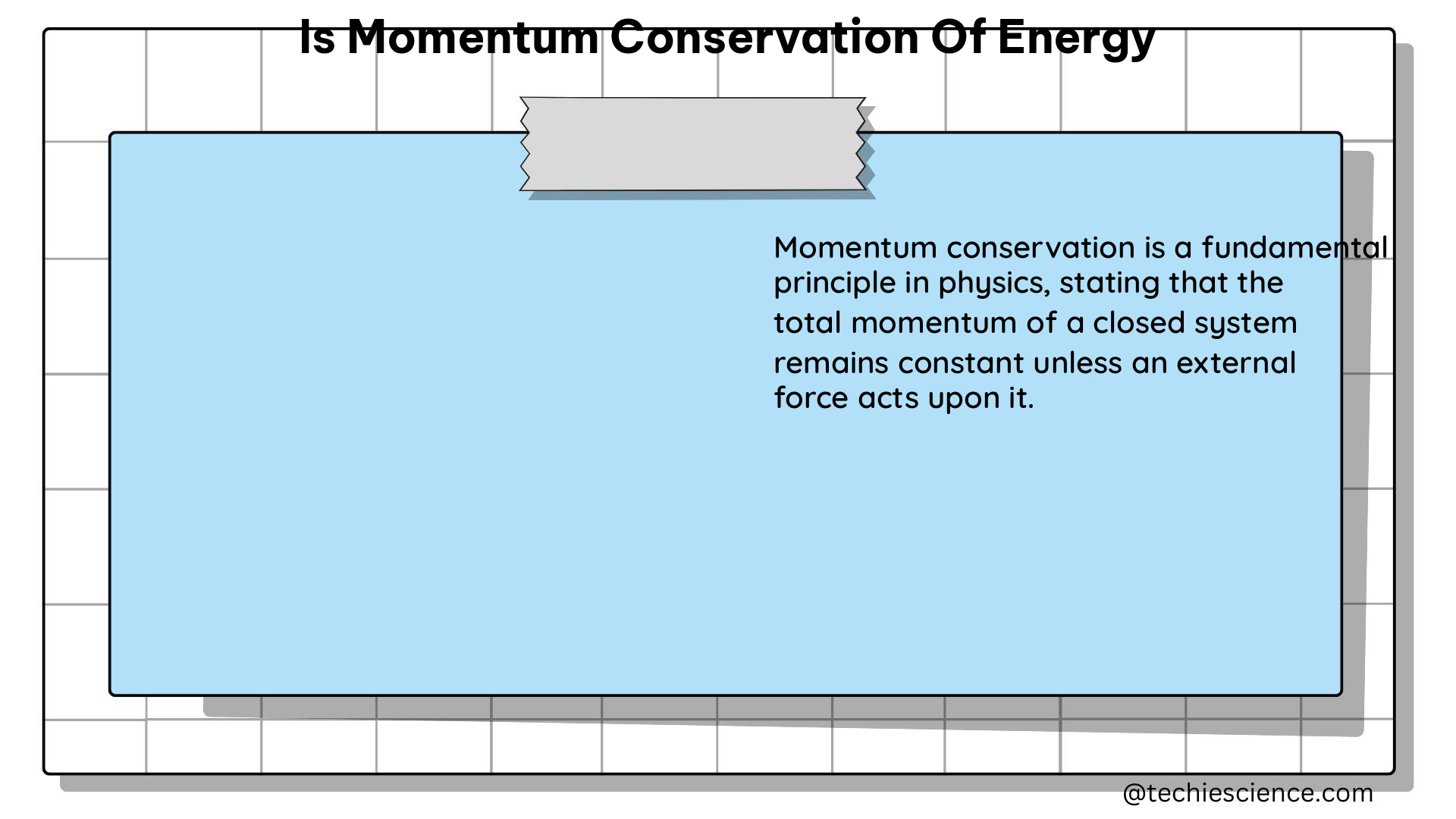
While the conservation of momentum and the conservation of energy are both fundamental principles in physics, they are not equivalent. The conservation of momentum states that the total momentum of a closed system remains constant, while the conservation of energy states that the total energy of a closed system remains constant.

The key difference is that momentum is a vector quantity, while energy is a scalar quantity. This means that momentum has both magnitude and direction, while energy only has magnitude. As a result, the conservation of momentum and the conservation of energy are governed by different physical laws and have different applications.

For example, in a perfectly elastic collision between two objects, both momentum and energy are conserved. However, in an inelastic collision, momentum is conserved, but some of the kinetic energy is converted into other forms of energy, such as heat or sound. In this case, the total energy is still conserved, but the distribution of energy between the different forms may change.

Examples of Conservation of Energy

The conservation of energy can be observed in various physical phenomena and systems. Here are some examples:

Pendulum Motion

When a pendulum is released from rest at a certain height, it begins to swing back and forth. As the pendulum swings, its potential energy is transformed into kinetic energy and back again, but the total mechanical energy remains approximately constant. Sample data from a pendulum lab might show that the pendulum’s kinetic energy and potential energy change as it swings, but the sum of the two remains relatively constant.

Roller Coaster Motion

At the beginning of a roller coaster ride, work is done to lift the car to its initial summit, giving it a large quantity of potential energy. As the car travels down hills and loops, its potential energy is transformed into kinetic energy, causing it to speed up. However, the total mechanical energy of the car remains constant, assuming no external forces are doing work on it. This means that the sum of the car’s kinetic energy and potential energy remains the same at every location along the track.

Ski Jumper Motion

As a ski jumper glides down a hill towards a jump ramp and off the ramp, potential energy is transformed into kinetic energy. If it can be assumed that no external forces are doing work on the ski jumper, then the total mechanical energy of the ski jumper is conserved. This means that the sum of the ski jumper’s kinetic energy and potential energy remains constant throughout the jump.

Nuclear Reactors

In nuclear reactors, mass can be converted to energy through nuclear reactions, and this energy can be harnessed to generate electricity. The conservation of energy is critical in ensuring that the total amount of energy in a nuclear reactor remains constant, even as mass is converted to energy.

Quantifying the Conservation of Energy

To quantify the conservation of energy, we can measure the kinetic energy and potential energy of an object at different points in time and show that the total mechanical energy remains constant, provided that no external forces are doing work on the system.

The kinetic energy of an object can be calculated using the formula:

K = (1/2) * m * v^2

Where:
– K is the kinetic energy of the object
– m is the mass of the object
– v is the velocity of the object

The potential energy of an object can be calculated using the formula:

U = m * g * h

Where:
– U is the potential energy of the object
– m is the mass of the object
– g is the acceleration due to gravity
– h is the height of the object above a reference point

By measuring the kinetic energy and potential energy of an object at different points in time and showing that their sum remains constant, we can demonstrate the conservation of energy in a given system.

Numerical Examples

Here are some numerical examples to illustrate the conservation of energy:

1. Pendulum Motion:
2. Initial height of the pendulum: 1.5 m
3. Mass of the pendulum: 0.5 kg
4. Potential energy at the highest point: U = m * g * h = 0.5 kg * 9.8 m/s^2 * 1.5 m = 7.35 J
5. Kinetic energy at the lowest point: K = (1/2) * m * v^2 = (1/2) * 0.5 kg * (3 m/s)^2 = 7.35 J

6. Total mechanical energy remains constant at 7.35 J.

7. Roller Coaster Motion:

8. Mass of the roller coaster car: 1000 kg
9. Initial height of the car: 50 m
10. Potential energy at the initial height: U = m * g * h = 1000 kg * 9.8 m/s^2 * 50 m = 490,000 J
11. Kinetic energy at the bottom of the first hill: K = (1/2) * m * v^2 = (1/2) * 1000 kg * (30 m/s)^2 = 450,000 J

12. Total mechanical energy remains constant at 490,000 J.

13. Ski Jumper Motion:

14. Mass of the ski jumper: 80 kg
15. Initial height of the jump ramp: 30 m
16. Potential energy at the initial height: U = m * g * h = 80 kg * 9.8 m/s^2 * 30 m = 23,520 J
17. Kinetic energy at the end of the jump: K = (1/2) * m * v^2 = (1/2) * 80 kg * (25 m/s)^2 = 12,500 J
18. Total mechanical energy remains constant at 23,520 J.

These examples demonstrate how the conservation of energy can be quantified by measuring the kinetic energy and potential energy of an object at different points in time and showing that their sum remains constant.

Conclusion

The conservation of energy is a fundamental principle in physics that states that the total energy in an isolated system remains constant over time. While momentum and energy are related, they are distinct physical quantities, and the conservation of momentum and the conservation of energy are governed by different physical laws.

By collecting measurable and quantifiable data on the kinetic energy and potential energy of various physical systems, it is possible to demonstrate the conservation of energy and show that the total mechanical energy remains constant, provided that no external forces are doing work on the system. This principle has important applications in fields such as mechanics, nuclear physics, and beyond.

References

1. Khan Academy. (2024). What is conservation of energy? Retrieved from https://www.khanacademy.org/science/physics/work-and-energy/work-and-energy-tutorial/a/what-is-conservation-of-energy
2. Physics Classroom. (n.d.). Analysis of Situations in Which Mechanical Energy is Conserved. Retrieved from https://www.physicsclassroom.com/class/energy/Lesson-2/Analysis-of-Situations-in-Which-Mechanical-Energy-is-Conserved
3. Physics Stack Exchange. (2020). Why is the conservation of momentum not equivalent to the conservation of energy? Retrieved from https://physics.stackexchange.com/questions/569028/why-is-the-conservation-of-momentum-not-equivalent-to-the-conservation-of-energy
4. Lumen Learning. (n.d.). Relativistic Energy. Retrieved from https://courses.lumenlearning.com/suny-physics/chapter/28-6-relativistic-energy/

Conservation of angular momentum describes the spinning property of a physical system in which the spin remains constant unless an external torque disturbs the system’s spin.

A list of conservation of angular momentum examples is given below.

• The spin of a figure skater
• Point mass rotating through the hollow tube
• Man on a rotating table holding a dumbbell
• Diver jumping to the water from height
• Gyrocompass in an airplane.
• Propellers of the helicopter
• Rotational collision of two objects
• Rotation of the earth
• Moon revolving around the earth
• Spinning the ball on a fingertip
• The spinning of top toys
• Wheels
• Ballet dancers spin
• Bowling game
• Gymnast
• Asteroids spinning freely in space
• Speed of wind in Tornadoes
• The spin of an electron
• Planetary motion
• Gyroscope

A detailed explanation of conservation of angular momentum examples

Angular momentum is a product of momentum inertia of rotational object times the angular velocity. It is also characterized by two other types: spin angular momentum and orbital angular momentum based on the orientation of rotation. This section gives a brief explanation regarding conservation angular momentum examples.

The spin of a figure skater

When a figure skater begins to spin on an ice rink with one arm extended, as soon as they spin faster with greater angular velocity and the arms are drawn inward, the moment of inertia is reduced; thus, angular momentum is conserved.

Point mass rotating through the hollow tube

Tie a point mass to one end of a string and rotate it in a vertical hollow tube; the point mass rotates in a horizontal circle with the constant angular momentum.

If the string is pulled down, the radius of the rotational axis reduces, and the torque will be zero; thus, angular momentum is conserved as the force acting on the point mass, and the string is radial.

Man on a rotating table holding a dumbbell

To explain the conservation of angular momentum examples assume that a man outstretches his arm holding a dumbbell and stand at the center of the rotating table.

When he pulls his arm inward, the speed of the rotational table increases as the distance between the center of rotation and the dumbbell decreases, which leads to an increase in the angular velocity and a decrease in the moment of inertia, thus the angular moment will remain constant being conserved.

Diver jumping to the water from height

A diver jumps to the water from a springboard by pulling his arms and legs towards the center of his body. By this action, the body’s moment of inertia decreases by subsequent angular velocity. The above action helps him to rotate his body in the air. So he does not keep his hand straight.

Gyrocompass in an airplane

Airplanes are fitted with the gyrocompass to relocate the geographical direction for navigation based on earth rotation. The gyrocompass consists of a spinning disc.

A spinning gyrocompass rotates freely independent of the aircraft’s motion, and its orientation remains constant. Thus the angular momentum of the gyrocompass is conserved in the airplane.

Propellers of the helicopter

A helicopter is provided with two propellers to balance the conservation of angular momentum.

If a helicopter is fitted with only one propeller, the helicopter body would have turned opposite to the direction of the propeller’s rotation due to the conservation of angular momentum. Thus for stability, two propeller shaft is required.

Rotational collision of two objects

Conservation of angular momentum in the rotational collision of two objects is an excellent way to explain the conservation of angular momentum examples.

Let us illustrate by considering an example. Suppose a ball collides with a stick, then the ball rotates at its end. When two objects collide, an angular impulse is exerted on both objects, which is equal and opposite to maintaining the total angular momentum constant.

Rotation of the earth

The angular momentum of the earth is fairly conserved while rotating because the earth exerts a gravitational force, which is a central and conservative force.

Moon revolving around the earth

The moon revolving around the earth possesses constant angular momentum due to the earth reducing its angular momentum due to drag or friction applied by the tides, which is gained by the moon. So the angular momentum is conserved on the moon.

Spinning the ball on a fingertip

When a ball is made to rotate on the fingertip, the total angular momentum of the ball is conserved until and unless an external force is triggered on the ball.

The spinning of top toys

When a top toy is made to spin, it gains angular momentum. This remains constant until an external torque is applied to it. The angular momentum gradually decreases due to friction between the surface and top toy.

Wheels

The angular momentum is associated with the wheels, such as the bicycle wheel and the rotating chair’s wheel.

When the wheel is subjected to spin, the torque acting on the wheel is nullified. Thus, the angular moment does not change and is conserved if the wheel rotates continuously.

Ballet dancers spin

The position of the ballet dancer during their performance involves stretching their arms and legs inward and outward while spinning. This action consequently increases or decreases the angular momentum and moment of inertia, thus conserving the angular momentum.

Bowling game

In the bowling game, the ball moves over the ramp by rotating and hits the pin, making it fall. The ball’s angular momentum after hitting the pin is also balanced by decreasing its moment of inertia.

Gymnast

Gymnasts are aware of the conservation of angular moment during their exercise. They have to curl their body towards their center of mass during the floor exercise, which is carried by conserving the angular momentum.

Asteroids spinning freely in space

Asteroids rotating freely in space have constant angular momentum as external torque would influence them.

Speed of wind in Tornadoes

In the inner layer of tornadoes, the speed at which the wind rotates is restricted by the law of conservation of angular momentum. They spin rapidly and gain angular velocity, leading to losing the moment of inertia. Hence the angular momentum is conserved.

The spin of an electron

The angular momentum demonstrates the electron revolving around the nucleus. Electrons also orbit around the nucleus. Their spin angular momentum is conserved in every aspect of spinning.

Planetary motion

All the planets around the sun in an elliptical orbit have constant angular momentum.

From Kepler’s second law of planetary motion, its mass remains the same, but the distance between the planet and the sun varies as the planet goes nearer to the sun and its speed increases. Thus angular momentum is conserved in planetary motion.

Gyroscope

In a gyroscope, the tendency of a rotating object to orient in a rotational axis must possess constant angular momentum. The gyroscope acquires the angular momentum in the torque direction and rotates on the horizontal axis.

Conservation of angular momentum problems

The angular momentum of any object is associated with angular velocity and the moment of inertia. Let us solve some conservation of angular momentum examples problems using all of them.

A ballet dancer has a moment of inertial of 3kgm² when the arm is pulled inward and 10kgm² when the arm is stretched outward. If the rotational speed of the dancer when the arm is inward is 14round/sec, calculate the dancer’s speed when the arm is stretched outward.

Solution:

Since the angular momentum is the product of the moment of inertia and angular velocity, we can write the equation as

Iω=I_sω_s

3×14=10×ω_s

42=10ω_s

ω_s=4.2rounds/sec.

A man is standing on a turntable rotating with angular velocity ω and moment of inertia of I with his arm towards the center of the body. When he extended his arm outward, the moment of inertial is increased by 4 times its original value. Calculate the new angular velocity.

Solution:

The conservation of angular momentum is

Iω=I’ω’

Let I and I’ be the moment of inertia when the arm is inward and extended, respectively, and ω and ω’ be the angular velocity when the arm is inward and extended, respectively.

I’=4I

Iω=4Iω’

Also Read:

• Energy momentum relation in particle
• How to find momentum in quantum mechanics
• How to find momentum for a photon
• Is momentum conserved in an isolated system
• Is momentum conserved in an elastic collision
• Is momentum conserved in an inelastic collision
• How to find momentum in fluid dynamics
• How to find momentum conservation in collisions
• How to find momentum of an electron
• How to find momentum from force time graph

Summary

Friction and angular momentum are fundamental concepts in physics that are closely related. Friction is a force that resists the motion of two surfaces in contact, while angular momentum is the rotational equivalent of linear momentum. This comprehensive guide provides measurable and quantifiable data on friction and angular momentum, along with technical specifications, theoretical explanations, and practical examples to help physics students deepen their understanding of these crucial topics.

Understanding Angular Momentum

Angular momentum is a measure of the rotational motion of an object and is given by the formula:

L = Iω

where:
– L is the angular momentum
– I is the moment of inertia
– ω is the angular velocity

The moment of inertia, I, is a measure of an object’s resistance to rotational motion and is calculated as:

I = ∑mr^2

where:
– m is the mass of the object
– r is the distance from the axis of rotation

The angular velocity, ω, is the rate of change of the angular displacement and is given by:

ω = dθ/dt

where:
– θ is the angular displacement
– t is the time

Understanding Friction

Friction is a force that resists the relative motion between two surfaces in contact and is described by the formula:

F = μN

where:
– F is the frictional force
– μ is the coefficient of friction
– N is the normal force

The coefficient of friction, μ, is a dimensionless quantity that depends on the materials in contact and the smoothness of the surfaces. The normal force, N, is the force exerted by an object perpendicular to the surface it is in contact with.

Relationship between Friction and Angular Momentum

Friction plays a crucial role in the conservation of angular momentum. When a system is rotating, friction can exert a torque on the system, which can change its angular momentum. However, if the torque due to friction is zero, then the angular momentum of the system is conserved.

To illustrate the relationship between friction and angular momentum, let’s consider the example of a solid cylinder rolling down an inclined plane without slipping, starting from rest. The free-body diagram and sketch are shown in Figure 11.5, including the normal force, components of the weight, and the static friction force.

The linear acceleration of the center of mass is given by:

a = (F - f)/m

where:
– a is the linear acceleration
– F is the force of gravity
– f is the force of friction
– m is the mass of the cylinder

The torque due to friction is given by:

τ = fr

where:
– τ is the torque
– f is the force of friction
– r is the radius of the cylinder

Applying Newton’s second law for rotation, we have:

Iα = τ

where:
– I is the moment of inertia
– α is the angular acceleration

Substituting the expression for torque, we have:

Iα = fr

The linear acceleration is related to the angular acceleration by:

a = rα

Substituting this expression, we have:

a = (f/m)r

Solving for f, we have:

f = (ma)/r

Substituting this expression into the condition for no slipping, we have:

ma ≤ μN

Solving for the acceleration, we have:

a ≤ μg

where g is the acceleration due to gravity.

Numerical Problems

Problem 1: Solid Cylinder Rolling Down an Inclined Plane

A solid cylinder of mass 2 kg and radius 0.2 m rolls down an inclined plane without slipping. The coefficient of static friction between the cylinder and the plane is 0.5. What is the acceleration of the cylinder?

Solution:
Using the formula for acceleration:
a = (f/m)r

Where:
– f is the force of friction, given by f = μN
– N is the normal force, given by N = mgcosθ
– m is the mass of the cylinder (2 kg)
– r is the radius of the cylinder (0.2 m)
– θ is the angle of the inclined plane (30°)
– μ is the coefficient of static friction (0.5)
– g is the acceleration due to gravity (9.8 m/s²)

Substituting the values, we get:
a = (μmgcosθ/m)r
a = (0.5)(9.8)(cos30°)(0.2)
a = 0.349 m/s²

Therefore, the acceleration of the cylinder is 0.349 m/s².

Problem 2: Solid Sphere Rolling on a Horizontal Surface

A solid sphere of mass 3 kg and radius 0.15 m is rolling on a horizontal surface with an initial angular velocity of 5 rad/s. The coefficient of kinetic friction between the sphere and the surface is 0.3. What is the angular velocity of the sphere after 10 seconds?

Solution:
Using the formula for angular momentum:
L = Iω

Where:
– L is the angular momentum
– I is the moment of inertia of the solid sphere, given by I = (2/5)mr^2
– ω is the angular velocity

The torque due to friction is given by:
τ = -fr

Where:
– τ is the torque
– f is the force of friction, given by f = μN
– N is the normal force, given by N = mg
– μ is the coefficient of kinetic friction (0.3)
– m is the mass of the sphere (3 kg)
– g is the acceleration due to gravity (9.8 m/s²)
– r is the radius of the sphere (0.15 m)

Applying Newton’s second law for rotation:
Iα = τ

Where:
– α is the angular acceleration

Substituting the expressions, we have:
(2/5)mr^2(dω/dt) = -μmgr
(dω/dt) = -(5/2)μg

Integrating this expression, we get:
ω(t) = ω(0) - (5/2)μgt

Substituting the given values:
ω(10 s) = 5 rad/s - (5/2)(0.3)(9.8)(10 s)
ω(10 s) = 0.75 rad/s

Therefore, the angular velocity of the sphere after 10 seconds is 0.75 rad/s.

Conclusion

Friction and angular momentum are closely related concepts in physics that are governed by specific formulas and principles. By understanding these concepts and their relationships, physics students can analyze and predict the motion of objects in a variety of contexts. This comprehensive guide provides the necessary technical details, theoretical explanations, and practical examples to help students deepen their understanding of these fundamental topics.

References

1. OpenStax, University Physics Volume 1. OpenStax CNX. Sep 19, 2016 http://cnx.org/contents/[email protected]
2. Quizlet, AP Physics Help Flashcards. Quizlet. https://quizlet.com/569499012/ap-physics-help-flash-cards/
3. ScienceDirect, Angular Momentum – an overview. ScienceDirect. https://www.sciencedirect.com/topics/earth-and-planetary-sciences/angular-momentum
4. UCF Pressbooks, 11.2 Conservation of Angular Momentum. UCF Pressbooks. https://pressbooks.online.ucf.edu/phy2048tjb/chapter/11-2-conservation-of-angular-momentum/
5. Quizlet, Torque & Angular Momentum FRQs Flashcards. Quizlet. https://quizlet.com/779935324/torque-angular-momentum-frqs-flash-cards/

The conservation of momentum is a fundamental principle in physics that states the total momentum of a closed system remains constant unless acted upon by an external force. Mathematically, it is expressed as ptot = constant or ptot = p'tot (isolated system), where ptot is the initial total momentum and p'tot is the total momentum some time later.

Identifying the System

The first step in finding the conservation of momentum in a system is to identify the system under consideration. This involves ensuring that the system is a closed system, meaning that no external forces are acting on it. To do this, you should:

1. Clearly define the boundaries of the system, including all the objects or particles involved.
2. Ensure that there are no external forces acting on the system, such as gravity, friction, or applied forces.
3. Verify that the system is isolated, meaning that it does not exchange momentum with its surroundings.

Calculating Initial Momentum

Once the system has been identified, the next step is to calculate the initial total momentum (ptot) of the system. This is done by summing the momentum of all individual objects or particles within the system. The momentum of an object is given by the formula:

p = m * v

where p is the momentum, m is the mass, and v is the velocity of the object.

To calculate the initial total momentum, you would use the following equation:

ptot = p1 + p2 + p3 + ... + pn

where p1, p2, p3, …, pn are the momenta of the individual objects or particles in the system.

Calculating Final Momentum

After any interactions or collisions within the system, the final total momentum (p'tot) of the system must be calculated. This is done in the same way as the initial total momentum, but using the final velocities of the objects or particles:

p'tot = m1 * v1f + m2 * v2f + m3 * v3f + ... + mn * vnf

where v1f, v2f, v3f, …, vnf are the final velocities of the individual objects or particles.

Comparing Initial and Final Momentum

The final step in finding the conservation of momentum is to compare the initial total momentum (ptot) and the final total momentum (p'tot). If the system is closed and no external forces are acting on it, the total momentum should remain constant, meaning that ptot = p'tot.

If the initial and final momenta are equal, then the system is said to conserve momentum. If they are not equal, then the system does not conserve momentum, and there must be an external force acting on the system.

Theorem and Formulas

The conservation of momentum is a fundamental principle in physics, and it can be expressed mathematically as:

Theorem: In an isolated system, the total momentum is conserved.

Formulas:
– Initial total momentum: ptot = p1 + p2 + p3 + ... + pn
– Final total momentum: p'tot = m1 * v1f + m2 * v2f + m3 * v3f + ... + mn * vnf
– Conservation of momentum: ptot = p'tot

Examples and Numerical Problems

Example 1: Two objects with masses m1 = 2 kg and m2 = 3 kg are moving with initial velocities v1i = 4 m/s and v2i = -2 m/s, respectively. After a collision, the final velocities are v1f = 1 m/s and v2f = 1 m/s. Verify the conservation of momentum.

Solution:
1. Initial total momentum: ptot = m1 * v1i + m2 * v2i = 2 * 4 + 3 * (-2) = 8 - 6 = 2 kg·m/s
2. Final total momentum: p'tot = m1 * v1f + m2 * v2f = 2 * 1 + 3 * 1 = 2 + 3 = 5 kg·m/s
3. Comparing initial and final momentum: ptot = 2 kg·m/s and p'tot = 5 kg·m/s, so the system does not conserve momentum.

Numerical Problem 1: A 2 kg object is moving with an initial velocity of 5 m/s, and a 3 kg object is moving with an initial velocity of -3 m/s. After a collision, the final velocities are 2 m/s and -1 m/s, respectively. Verify the conservation of momentum.

Numerical Problem 2: Two objects with masses 4 kg and 6 kg are moving in opposite directions with initial velocities of 3 m/s and -2 m/s, respectively. After a perfectly elastic collision, the final velocities are 1 m/s and -1 m/s, respectively. Verify the conservation of momentum.

Figures and Data Points

To better illustrate the concept of conservation of momentum, consider the following figure:

In this figure, two objects with masses m1 and m2 are moving with initial velocities v1i and v2i, respectively. After a collision, the final velocities are v1f and v2f.

The data points for this example are:
– m1 = 2 kg
– m2 = 3 kg
– v1i = 4 m/s
– v2i = -2 m/s
– v1f = 1 m/s
– v2f = 1 m/s

Conclusion

In summary, to find the conservation of momentum in a system, you must:

1. Identify the system as a closed system with no external forces acting on it.
2. Calculate the initial total momentum (ptot) by summing the momenta of all individual objects or particles.
3. Calculate the final total momentum (p'tot) after any interactions or collisions, using the final velocities of the objects or particles.
4. Compare the initial and final momenta to determine if the system conserves momentum (ptot = p'tot).

By following these steps and applying the relevant formulas and theorems, you can accurately determine whether a system conserves momentum or not. This principle is fundamental in various fields of physics, from classical mechanics to quantum physics.

Reference:

1. http://hadron.physics.fsu.edu/~crede/TEACHING/PHY2053C/LAB-MANUALS/linearmomentum-1.pdf
2. https://courses.lumenlearning.com/suny-physics/chapter/8-3-conservation-of-momentum/
3. https://www.youtube.com/watch?v=SMebmMRS_2Q

Gravity and angular momentum are two fundamental concepts in physics that are closely intertwined. Gravity is the force that attracts objects towards each other, while angular momentum is a measure of an object’s rotational motion in space-time. Understanding the intricate relationship between these two principles is crucial for a deep comprehension of various physical phenomena, from the dynamics of celestial bodies to the behavior of subatomic particles.

Gravity: Quantifying the Attractive Force

Gravity is a universal force that governs the motion of objects in the universe. The strength of the gravitational force between two objects is determined by their masses and the distance between them, as described by Newton’s law of universal gravitation:

F = G * (m1 * m2) / r^2

Where:
– F is the gravitational force
– G is the gravitational constant (6.674 × 10^-11 N⋅m^2/kg^2)
– m1 and m2 are the masses of the two objects
– r is the distance between the objects

This formula allows us to quantify the gravitational force between any two objects, provided we know their masses and the distance separating them. It is important to note that gravity is an inverse-square law, meaning that the gravitational force decreases rapidly as the distance between the objects increases.

Experimental Measurements of Gravity

Measuring the gravitational force between two objects, especially at the atomic or molecular scale, is a challenging task due to the extremely small magnitudes involved. However, researchers have developed sophisticated techniques to measure gravity at these scales.

One notable experiment was conducted by the Eöt-Wash group at the University of Washington, where they used a torsion balance to measure the gravitational force between two tungsten masses, each weighing approximately 10 kilograms. The experiment was able to measure the gravitational force with an accuracy of 1 part in 10^11, providing a precise determination of the gravitational constant, G.

In addition to these direct measurements, gravity has also been indirectly observed through its effects on the motion of celestial bodies, the bending of light by massive objects (gravitational lensing), and the detection of gravitational waves.

Angular Momentum: Quantifying Rotational Motion

Angular momentum is a vector quantity that describes the rotational motion of an object around a specific axis. It is defined as the product of the object’s moment of inertia (I) and its angular velocity (ω):

L = I * ω

Where:
– L is the angular momentum
– I is the moment of inertia, which depends on the object’s mass distribution
– ω is the angular velocity of the object

The conservation of angular momentum is a fundamental principle in physics, stating that the total angular momentum of a closed system remains constant unless an external torque is applied. This principle has important implications in various fields, from the dynamics of rotating machinery to the behavior of celestial bodies.

Measuring Angular Momentum

Measuring the angular momentum of an object can be done using a variety of techniques, depending on the specific system and the desired level of precision. Some common methods include:

1. Rotational Dynamics Experiments: By measuring the torque applied to an object and its resulting angular acceleration, the angular momentum can be calculated using the formula L = I * α, where α is the angular acceleration.

2. Optical Techniques: Laser interferometry and other optical methods can be used to precisely measure the angular velocity of an object, which can then be used to calculate its angular momentum.

3. Spectroscopic Measurements: The angular momentum of atoms and molecules can be determined by analyzing their spectroscopic signatures, which are influenced by the object’s rotational state.

4. Neutron Scattering: The angular momentum of subatomic particles, such as neutrons, can be measured by studying their scattering patterns when interacting with other particles or materials.

These experimental techniques have been instrumental in advancing our understanding of angular momentum and its role in various physical phenomena.

Gravity and Angular Momentum in Astrophysics

The interplay between gravity and angular momentum is particularly evident in the study of astrophysical objects, such as black holes, neutron stars, and binary systems.

Gravitational Waves and Angular Momentum

Gravitational waves are ripples in the fabric of space-time, produced by the acceleration of massive objects. These waves carry away energy and angular momentum from the system, causing it to lose stability and eventually merge.

The Laser Interferometer Gravitational-Wave Observatory (LIGO) and other gravitational wave detectors have been able to measure the gravitational waves produced by the merger of black holes and neutron stars. By analyzing the waveform of these signals, researchers can extract valuable information about the properties of the objects, including their masses, spins, and orbital angular momentum.

Black Holes and Angular Momentum

Black holes are some of the most extreme objects in the universe, and their behavior is heavily influenced by their angular momentum. The spin of a black hole is directly related to its angular momentum, and this property can have significant implications for the dynamics of matter and energy around the black hole.

For example, the spin of a black hole can affect the accretion of matter onto the black hole, the formation of jets, and the emission of radiation. Understanding the angular momentum of black holes is crucial for understanding their overall behavior and the processes that occur in their vicinity.

Binary Systems and Angular Momentum

Binary systems, consisting of two orbiting celestial bodies, are another example of the importance of angular momentum in astrophysics. The orbital angular momentum of a binary system plays a crucial role in its stability and evolution.

As the binary system loses energy and angular momentum, for example, through the emission of gravitational waves, the two objects can eventually merge, leading to the formation of a single, more massive object. The study of binary systems and their angular momentum has provided valuable insights into the formation and evolution of various astrophysical objects, including black holes and neutron stars.

Numerical Examples and Problems

To further illustrate the concepts of gravity and angular momentum, let’s consider some numerical examples and problems:

Example 1: Gravitational Force between Two Masses

Suppose two masses, m1 = 10 kg and m2 = 5 kg, are separated by a distance of 1 meter. Calculate the gravitational force between them.

Given:
– m1 = 10 kg
– m2 = 5 kg
– r = 1 m

Using the formula for gravitational force:
F = G * (m1 * m2) / r^2
F = (6.674 × 10^-11 N⋅m^2/kg^2) * (10 kg * 5 kg) / (1 m)^2
F = 3.337 × 10^-9 N

Problem 1: Calculating Angular Momentum

A solid sphere with a mass of 2 kg and a radius of 0.5 m is rotating at an angular velocity of 10 rad/s. Calculate the angular momentum of the sphere.

Given:
– m = 2 kg
– r = 0.5 m
– ω = 10 rad/s

To calculate the angular momentum, we need to find the moment of inertia of the sphere first:
I = (2/5) * m * r^2
I = (2/5) * 2 kg * (0.5 m)^2
I = 0.25 kg⋅m^2

Now, we can calculate the angular momentum:
L = I * ω
L = 0.25 kg⋅m^2 * 10 rad/s
L = 2.5 kg⋅m^2/s

Example 2: Gravitational Waves and Angular Momentum

Consider a binary system consisting of two black holes, each with a mass of 30 solar masses (M_sun = 1.989 × 10^30 kg). The black holes are separated by a distance of 100 km and are orbiting each other at an angular velocity of 1 rad/s.

Calculate the total angular momentum of the binary system.

Given:
– m1 = m2 = 30 M_sun = 30 * 1.989 × 10^30 kg = 5.967 × 10^31 kg
– r = 100 km = 1 × 10^5 m
– ω = 1 rad/s

To calculate the total angular momentum, we need to find the moment of inertia of the binary system first:
I = m1 * r^2 + m2 * r^2
I = (5.967 × 10^31 kg) * (1 × 10^5 m)^2 + (5.967 × 10^31 kg) * (1 × 10^5 m)^2
I = 5.967 × 10^39 kg⋅m^2

Now, we can calculate the total angular momentum:
L = I * ω
L = 5.967 × 10^39 kg⋅m^2 * 1 rad/s
L = 5.967 × 10^39 kg⋅m^2/s

This large value of angular momentum is typical for binary systems involving massive objects like black holes, and it plays a crucial role in the dynamics and evolution of these systems, including the emission of gravitational waves.

Conclusion

Gravity and angular momentum are fundamental concepts in physics that are deeply interconnected. Understanding the quantifiable aspects of these principles, including the formulas, experimental measurements, and their applications in astrophysics, is essential for a comprehensive understanding of the physical world.

By exploring the numerical examples and problems presented in this guide, physics students can develop a stronger grasp of the practical applications of gravity and angular momentum, and how these concepts shape the behavior of various physical systems, from the microscopic to the cosmic scale.

References

1. Quizlet – Phy Flashcards: https://quizlet.com/589600152/phy-flash-cards/
2. Physics Stack Exchange – Has gravity ever been experimentally measured between two atoms?: https://physics.stackexchange.com/questions/130594/has-gravity-ever-been-experimentally-measured-between-two-atoms
3. Quanta Magazine – Mass and Angular Momentum, Left Ambiguous by Einstein, Get Defined: https://www.quantamagazine.org/mass-and-angular-momentum-left-ambiguous-by-einstein-get-defined-20220713/
4. Springer – Gravitational waves with orbital angular momentum: https://link.springer.com/article/10.1140/epjc/s10052-020-7881-2

Angular momentum is a fundamental concept in classical mechanics that describes the rotational motion of an object around a fixed axis. It is a crucial quantity in understanding the dynamics of rotating systems, from the motion of planets to the spin of a basketball. In this comprehensive guide, we will delve into the details of how to calculate angular momentum with mass, providing you with a thorough understanding of the underlying principles and practical applications.

Understanding Angular Momentum

Angular momentum, denoted as L, is a vector quantity that represents the product of an object’s moment of inertia (I) and its angular velocity (ω). The formula for angular momentum is:

L = I × ω

Where:
– L is the angular momentum (in kg·m²/s)
– I is the moment of inertia (in kg·m²)
– ω is the angular velocity (in rad/s)

The moment of inertia (I) is a measure of an object’s resistance to changes in its rotational motion. It depends on the distribution of the object’s mass around the axis of rotation. For a point mass, the moment of inertia is given by:

I = m × r²

Where:
– m is the mass of the object (in kg)
– r is the distance from the axis of rotation (in m)

The angular velocity (ω) is a measure of how fast an object is rotating around a fixed axis. It is given by the formula:

ω = v / r

Where:
– v is the linear velocity of the object (in m/s)
– r is the radius of the circular path (in m)

Calculating Angular Momentum for a Point Mass

To find the angular momentum of a point mass, we can use the formula:

L = m × v × r

Where:
– L is the angular momentum (in kg·m²/s)
– m is the mass of the object (in kg)
– v is the linear velocity of the object (in m/s)
– r is the distance from the axis of rotation (in m)

Let’s consider an example:

Suppose we have a point mass with a mass of 2 kg, a linear velocity of 5 m/s, and a distance from the axis of rotation of 3 m. We can calculate the angular momentum as follows:

L = m × v × r
L = 2 kg × 5 m/s × 3 m
L = 30 kg·m²/s

This formula can be used to calculate the angular momentum of a single point mass. However, in many real-world situations, we need to consider the angular momentum of a system of particles or a rigid body.

Angular Momentum of a System of Particles

To find the angular momentum of a system of particles, we need to sum the angular momenta of all the individual particles. The formula for the total angular momentum of a system of n particles is:

L_total = Σ (m_i × v_i × r_i)

Where:
– L_total is the total angular momentum of the system (in kg·m²/s)
– m_i is the mass of the i-th particle (in kg)
– v_i is the linear velocity of the i-th particle (in m/s)
– r_i is the distance from the axis of rotation to the i-th particle (in m)

For example, consider a system of three particles with the following properties:

Particle	Mass (kg)	Linear Velocity (m/s)	Distance from Axis (m)
1	2	5	3
2	3	4	2
3	1	6	4

To find the total angular momentum of the system, we can use the formula:

L_total = (2 kg × 5 m/s × 3 m) + (3 kg × 4 m/s × 2 m) + (1 kg × 6 m/s × 4 m)
L_total = 30 kg·m²/s + 24 kg·m²/s + 24 kg·m²/s
L_total = 78 kg·m²/s

Angular Momentum of a Rigid Body

For a rigid body, the angular momentum can be calculated using the formula:

L = I × ω

Where:
– L is the angular momentum of the rigid body (in kg·m²/s)
– I is the moment of inertia of the rigid body (in kg·m²)
– ω is the angular velocity of the rigid body (in rad/s)

The moment of inertia (I) of a rigid body depends on the distribution of its mass around the axis of rotation. For common shapes, the moment of inertia can be calculated using the following formulas:

• Solid sphere: I = (2/5) × m × r²
• Hollow sphere: I = (2/3) × m × r²
• Solid cylinder: I = (1/2) × m × r²
• Hollow cylinder: I = (1/2) × m × (r₁² + r₂²)
• Thin rod: I = (1/12) × m × L²

Where:
– m is the mass of the rigid body (in kg)
– r is the radius of the rigid body (in m)
– L is the length of the rigid body (in m)
– r₁ and r₂ are the inner and outer radii of the hollow cylinder (in m)

Let’s consider an example of a solid sphere with a mass of 5 kg and a radius of 0.5 m, rotating at an angular velocity of 2 rad/s. We can calculate its angular momentum as follows:

I = (2/5) × 5 kg × (0.5 m)²
I = 0.25 kg·m²

L = I × ω
L = 0.25 kg·m² × 2 rad/s
L = 0.5 kg·m²/s

Advanced Techniques and Applications

In addition to the basic formulas and examples provided, there are several advanced techniques and applications of angular momentum that you may encounter in more complex physics problems:

1. Conservation of Angular Momentum: The principle of conservation of angular momentum states that the total angular momentum of an isolated system remains constant unless an external torque acts on the system. This principle has numerous applications in fields like astronomy, robotics, and sports.

2. Angular Momentum in Quantum Mechanics: In quantum mechanics, angular momentum is a fundamental quantity that describes the rotational motion of subatomic particles. The quantization of angular momentum is a crucial aspect of quantum theory.

3. Angular Momentum in Rotational Dynamics: Angular momentum plays a central role in the analysis of rotational dynamics, such as the motion of gyroscopes, the precession of a spinning top, and the stability of rotating systems.

4. Angular Momentum in Orbital Mechanics: In the study of orbital mechanics, angular momentum is used to describe the motion of planets, satellites, and other celestial bodies around a central body, such as the Sun or a planet.

5. Angular Momentum in Biomechanics: In the field of biomechanics, the analysis of angular momentum is essential for understanding the dynamics of human movement, such as the motion of limbs during sports activities or the stability of the human body during various tasks.

These advanced topics and applications of angular momentum require a deeper understanding of the underlying principles and the ability to apply them in more complex scenarios. As you continue your studies in physics, you may encounter these concepts and be able to build upon the foundation laid in this comprehensive guide.

Conclusion

In this comprehensive guide, we have explored the fundamental concepts of angular momentum and how to calculate it with mass. We have covered the formulas for finding angular momentum of a point mass, a system of particles, and a rigid body, along with relevant examples and numerical problems. Additionally, we have touched upon some advanced techniques and applications of angular momentum in various fields of physics.

By mastering the concepts presented in this guide, you will be well-equipped to tackle a wide range of physics problems involving rotational motion and angular momentum. Remember to practice regularly, apply the principles to different scenarios, and continuously expand your knowledge to become a true expert in this fascinating area of classical mechanics.

References

1. Physics LibreTexts: Angular Momentum In Two Dimensions
2. Dummies: How to Calculate Angular Momentum
3. Khan Academy: Angular Momentum (video)
4. YouTube: How to Calculate Moment of Inertia & Angular Momentum in Human Movement
5. Hyperphysics: Angular Momentum
6. MIT OpenCourseWare: Rotational Dynamics and Angular Momentum
7. University of Cambridge: Angular Momentum