In this article, we will discuss what zero velocity is, how and when does it come into the scenario with some examples.
An object standing fixed at a point, or on a rigid body and does not displace with time then the velocity of an object is zero.
What is Zero Velocity?
The velocity of the object is defined as a change in its position along with time.
When there is no displacement of the object, the velocity of the object is said to be zero velocity.
The following graph shows the relation between displacement v/s time for zero velocity.
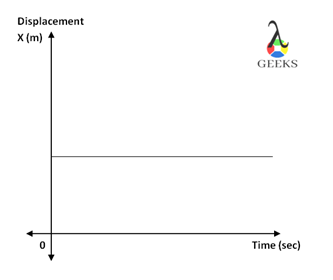
The above graph shows a straight line parallel to the x-axis, which says that the position of the object is the same for all the times; the position of the object does not change. This implies that the object is at rest, which means that the velocity of the object is nil.
When is Velocity Zero?
The object has zero velocity when it does not displace with time.
The velocity of the object is zero when there is no displacement of the object. The position of the object between two different time intervals remains the same.
The velocity is given by the relation v=(Δx/Δt)=(x2-x1)/(t2-t1)
For velocity to be zero =x2-x1; which is understood that the position of the object remains the same. Hence,
v=(x2-x1)/(t2-t1)=0
Problem: A block of mass ‘m’ was displaced at a distance of 300m and reaches point A at 12.05 pm. It was found that at 12.20 pm the block was present on the same position, that is 300 meters away from the original position. Find the velocity of the block.
Given: x1=300, x2=300, t1=12.05, t2=12.20
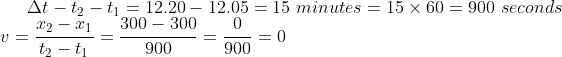
Hence, the velocity of the block is zero.
Zero Velocity Example
Objects at rest, have zero velocity. For example, a ball accelerating comes to a rest, a car climbs up the hill and a driver parks the car there, a coconut fell on the ground, a bird sitting on the branches of a tree, a rock standing on the edge of the mountain, etc.
The objects which are not movable are also examples of zero velocity. Examples are trees, mountains, tables, buildings, chairs, freezers, etc.
What is Zero Group Velocity?
A group, suggests the combination of two or more velocities. The velocity of the object is considered as a form of a wave when it is traveling, hence called a wave velocity.
Two or more waves traveling in a group modulates into a single wave. When the group velocity is zero, the waves diminish into a phase velocity that travels as a single wave, also when it travels through a node or vanishes.
Consider a wave propagating in the x-direction, and then the wave function associated with the wave is
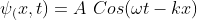
Where A is a amplitude of a wave
ω is a angular frequency which is given by the relation ω=2πt=2πf
k is a wave number, given by k=2πλ
λ is a wavelength
f is a frequency
When a single wave is propagating from a medium, then the velocity of that wave is called a phase velocity and is defined as the ratio of the angular frequency of the wave and the wave number, given by the equation
Vphase=ω/k
This is equal to the number of vibrations seen at two different points in the path length of the wave.
When two or more waves overlap and are modulated into a single wave pattern having the same velocity then the resultant velocity on a combination of all the waves forming a group is called group velocity.
Hence it is derivative of all the phase velocities of individual waves, given by the relation
Vgroup=dω/dk
When is Group Velocity Zero?
The group velocity is zero at the nodes of a modulated frequency, and when it overlaps with another wave.
When two waves of the same frequencies interfere with each other from the opposite direction, then the group velocity becomes zero.
The single wavelength of the same frequency and amplitude interfere with the group wave and propagates in the direction opposite to the group wave having the same phase velocity, then the group velocity of the waves vanishes and then merges into a single carrier wave.
Read more on Group Velocity.
Zero Instantaneous Velocity
The instantaneous velocity is stated as the displacement of the object that occurred in a very small time interval along its path.
The instantaneous center velocity is zero for the mass at the center of the object which is traveling along with the object moving at a certain velocity.
The instantaneous velocity is given by the formula

- Where Δt is a small interval of time
- Vi is Instantaneous Velocity
- x is a displacement
- t is a time
If an object accelerating in the x-direction, suddenly falls vertical down in negative y-direction, then the displacement of the object will be zero and hence the instantaneous velocity will be zero.
When is Instantaneous Velocity Zero?
The instantaneous velocity will be zero if there is a quick motion without acceleration in a short span.
If the body is in a motion but a part of it is connected rigidly to a certain point on another object, then the instantaneous velocity of that object is zero at that point.
Some examples of zero instantaneous velocity are an object rotating, skipping the rope with two ends of the rope fixed in hand, a woman doing a hula-hoop where the hula-hoop is in motion while the position of a woman is constant hence the velocity of a woman is nil, a point made by the tire of the vehicle attached to the road, the instantaneous velocity at that point is zero, ladder with clamp, compass and divider, and there are various other examples.
Zero Horizontal Velocity
When the object is in a projectile motion, we come across both horizontal and vertical velocity of the object. When the object does not move parallel to the ground then we have zero horizontal velocity.
The projectile motion of the object is shown in the below graph
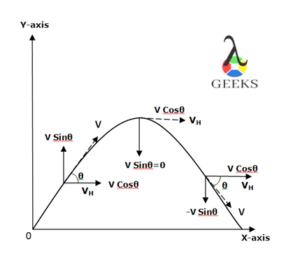
The y-axis represents the vertical motion of the object and the x-axis represents the horizontal displacement. The vertical velocity is given by the Sin function whereas the horizontal velocity is given by the Cosine function. When the object attains the highest position in its flight, at this point it has converted all its kinetic energy into potential energy and moves parallel to the surface and the vertical velocity of the object is nil. The object is for a longer duration in the air at this point.
When is Horizontal Velocity Zero?
If there is no horizontal displacement of an object the horizontal velocity will be equal to zero.
For a horizontal velocity to be zero, the object must not be in a projectile motion which is a two-dimensional motion, the object must be directed in a y-axis direction.
Lets us demonstrate zero horizontal velocity with a 2-D plot.
Consider a flight of the object of mass ‘m’ in the vertical direction from a fixed point on the horizontal surface. Consider the x-axis as a horizontal surface and the y-axis perpendicular to the x-axis.
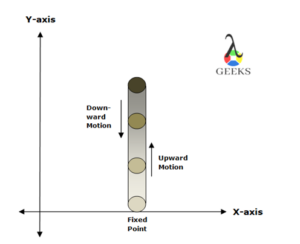
This position of the object in the horizontal axis remains fixed before and after the flight of the object. The object moves in a vertically upward direction due to kinetic energy, converts all the kinetic energy into potential energy, and returns back to the ground vertically downward without accelerating in a direction parallel to the surface.
Since there is no change in the position of the object even after the flight; the horizontal velocity of the object is zero. On contrary, there is a vertical displacement of the object which increases and decreases with time. Hence, the object is associated with both positive as well as negative velocity and acceleration.
Zero Velocity and Positive Acceleration
The velocity of the object is zero if there is no displacement, and we will have positive acceleration when there is a change in speed and the direction of motion of the object.
Hence, if the direction of the motion of the object changes frequently then the resultant velocity will be zero and the acceleration will be present.
The object decelerating will come to a rest where its velocity becomes zero and then move with the positive acceleration reversing its direction of the previous motion. Henceforth, we can have positive acceleration with zero velocity of the object.
Zero Uniform Velocity Motion
The object is said to have zero uniform velocity when there is no change in its motion with respect to time and it has no direction.
It is similar to the relative velocity where the velocity of the object appears to be constant for an observer moving at the same velocity and direction.
This is when the object is fixed to the rigid body and it does not displace with time and continue to be in the state of rest. The velocity of such an object is zero.
Consider a rectangular slab moving on a horizontal smooth surface. A donut shape articulate is attached on a rectangular slab which is moving along with the slab.
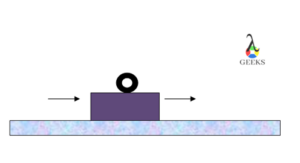
As the rectangular slab is displacing from one position to another, the position of the articulate remains fixed on the slab. Hence, the velocity of the articulate is zero.
Zero Relative Velocity
If the two objects are traveling at the same velocity and in the same direction then the relative velocity of each with respect to each other will be zero. This is represented as the zero relative velocity.
If two or more objects are traveling in the same direction then their speed cancels out and if the objects are moving in the opposite direction to each other, then their relative will be the sum of the speed of both the objects.
Let the velocities of two different objects be VA and VB. If these objects are moving in the same direction then their relative velocity is V= VA – VB; and if these objects are moving in the opposite direction, then their relative velocity will become V= VA – (-VB)= VA + VB.
Following is a position-time graph for two objects moving will equal speed and direction with time.

Since, both the objects are moving in the same direction their relative velocity is the vector difference of the velocities of both the objects. As both the objects are moving with the same velocities, the relative velocity of the object with respect to each other will be zero.
Consider two cars, Car A and Car B moving in the same lane driving at the same speed. A driver from car A can see a car B moving along with his car and the velocity of car B with respect to Car A is zero. The same is the case when a driver from Car B looks from his point of reference. Hence, the relative velocity of both cars with respect to each other is zero.
Problem: Consider two friends walking in the park with a velocity of 1.5 m/s. A man who is running at a speed of 2m/s in the park in a circle crosses the girls at a certain point. What is the relative velocity of a girl with respect to each other and that of a man?
Given: Velocity of both the girls VG=1.5m/s
The velocity of a man VM=2m/s
The direction of motion of both the girls in the same direction and velocity is equal.
V= VG-VG=1.5m/s – 1.5m/s=0
Hence, the relative velocity of girls with respect to each other is zero.
A man is also moving in the same direction but with unequal velocity. Therefore relative velocity of a man with that of girls is
V= VG-VM=1.5 m/s – 2 m/s= -0.5 m/s.
Hence, the relative velocity of girls with respect to a man is -0.5m/s which is negative. On the contrary, the relative velocity of a man with respect to girls is 0.5 m/s.
Read more on Negative Velocity And Zero Acceleration: How, When, Example And Problems.
Frequently Asked Questions
Q1. Find the instantaneous velocity of the object in a planar motion if the displacement of the object is given by the relation 2t3+2t+3 at time t= 5 seconds.
Given: The position of the object x=2t3+2t+3
The instantaneous velocity of the object is given by

The instantaneous velocity of the object is 152 m/s.
Q2. An object travels a distance of 6 meters in 2 seconds and then reverses its direction and moves again 6 meters in 2 seconds. Then calculate the displacement and the velocity of the object.
The object across 6 m in 2s, then the initial velocity of the object is
v1=x/t=6/2=3m/s
Then the object reverses its direction and travels the same distance in equal interval of time, hence the final velocity is
v2=x/t=-6/2=-3m/s
here displacement is negative because the direction of the motion of an object is in the opposite direction.
Hence, the resultant velocity is
V=v2+v1=-3+3=0
Since the resultant velocity of the object is zero, the displacement of the object is nil.
Q3. A ball is thrown in the air goes high vertically at a distance of 10 meters and returns down in the same plane after 10 seconds. Measure the vertical and horizontal velocity of the ball.
The time taken for a flight is 10 seconds and the distance covered by the ball in 10 seconds is 20 meters. Hence the velocity of the ball is
v=x/t=20/10=2m/s
Since there is no motion of an object in the horizontal direction; the horizontal velocity of the object is zero.
VH=0
An object round in shape is moving on a semi arc surface which is 40 cms long in 2 seconds. At what point the instantaneous velocity of the object will be seen?
The instantaneous velocity will be observed throughout the path of the motion.
Well, the velocity of the object will be maximum while accelerating down to a midpoint on the semi-arc surface.
Is trampoline an example of zero horizontal velocity?
A trampoline can be an example of zero horizontal velocity.
The motion of the body is in the vertical direction. The body is thrown upward and then returns down in the same vertical plane and there is no horizontal velocity and the direction attained by the body.
Also Read:
- How to determine velocity in molecular orbitals
- How to determine velocity in quantum decoherence
- How to determine velocity in cosmic inflation
- How to compute velocity in superstring theory
- What is the horizontal velocity of a projectile
- Negative velocity and zero acceleration
- Velocity of sound in air 2
- Centripetal acceleration and velocity
- How to find velocity of an object
- How to find delta velocity
Hi, I’m Akshita Mapari. I have done M.Sc. in Physics. I have worked on projects like Numerical modeling of winds and waves during cyclone, Physics of toys and mechanized thrill machines in amusement park based on Classical Mechanics. I have pursued a course on Arduino and have accomplished some mini projects on Arduino UNO. I always like to explore new zones in the field of science. I personally believe that learning is more enthusiastic when learnt with creativity. Apart from this, I like to read, travel, strumming on guitar, identifying rocks and strata, photography and playing chess.