Tension

In this article, we are going to discuss the dissimilarity between tension vs compression briefly and with detailed facts.

The following is a table differentiating between tension vs compression:-

Tension	Compression
Tensional force stretches the object tightly but the length of the object remains unchanged.	Compression is a force applied to reduce the volume or size of the object.
Tension is applied all across the string, rope, or spring due to pulling.	A string or rope can’t be compressed whereas the spring can be compressed.
The dimension of the object is unvaried.	The dimension of the object reduces on compression.
Stress on tension is called tensile stress that is responsible to pull the object away from each other.	Stress on compression is called compressive stress reduces the volume of the object.
The tension in one object makes action-reaction pairs in the opposite direction to each other.	The action-reaction pair due to the compression forces acts towards each other in one axis.
Tension on the string depends upon the mass and acceleration of the object it is attached to, and the net force acting on the object.	Compression depends upon the length, volume, area, density, and force applied to the object.
For an elastic object, the length of the object is increased on tension.	The length of the elastic object decreases on compression.
The force is transmitted through the object	The force is imposed on the object
The density of the object slightly reduces or remains unvaried	The density of the object increases
It is applicable only in 1 dimension	It is applicable in all the dimensions
Examples of tension forces are pendulums, rope bridges, hot air balloons, parachutes, rubber bands, elevators, kites, objects hanging on a hook, etc.	Examples of compression are squeezing a lemon, sponge, compressing spring, pumping, rolling a chapatti, concrete, etc.
Tension separates the objects away from each other.	Compression brings the objects closer to each other.
This is applicable only for string, springs, or ropes.	This is applicable to all materials except rope or strings.
Tension in the objects results in the deformation of the object	Compression results in contraction of the object
Tension is always positive.	The compression is a negative tension.

Tension and Compression Forces

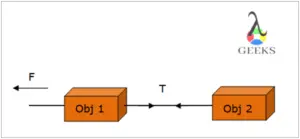
Basically, tension is created due to the action of pulling. The stretching of the rope or string does not change the length of the string, and the displacement between the objects connected by a string remains the same throughout that is if we observe object 2 from the frame of reference of object 1 then object 2 will appear to be stationary with respect to object 1.

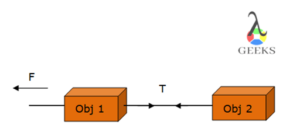
On contrary, the compression is a result of pressure exerted on the object from more than one direction, which consequences in the reduction of the volume and dimensions of the object. Due to a reduction in volume, the molecules per unit volume in the body of the object increases, and hence the density on compression increases. Well, this is not the case for the object undergoing tension.

Unlike tension, this is not exerted across the string or rope, the force due to tension is transmitted. Compression is also called a pushed force whereas tension occurs due to pulling. A tension is felt across the length between the two ends of the object whereas the compression takes place where the pressure on the area is imposed.

Read more on Tension Between Two Blocks: Several Entities And Problem Examples.

Tension and Compression in Bridges

Bridges undergo compression and tension at the same time. The tension comes into the act at the ends of the bridge and the tower of the bridge which supports the load of the bridge undergoes compression. Due to compression on one end of the pole, the tensional force is experienced on the other end of the pole.

When the heavy objects are carried from the bridge, the bridge is compressed due to a load, and the tension is felt underneath the base area of the bridge across the length between two poles of the bridge that support to withstand the load.

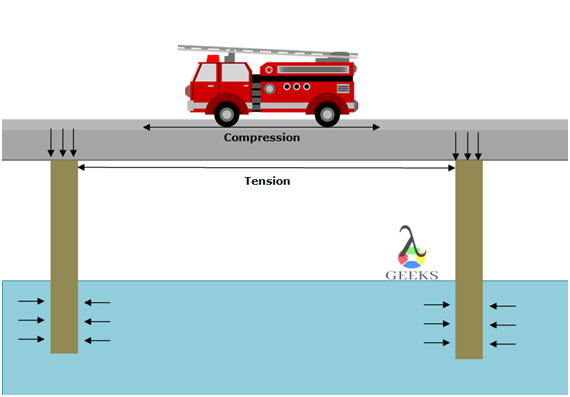
If the poles of the bridge are standing in the water bodies, then the water sagging on the walls of the poles also applies compressive force. The compressive force of the bridge is felt on the adjoining end of the poles. Tension is created across the length of the bridge between these two poles acting towards the poles. The tension forming in the bridge helps to withstand it with the compressive force exerting on it.

If you consider a suspension bridge, the cables are anchored on the bridge and are stretched and tightened to the pole. These cables go under tension when driven by the load across them, to sustain their position and provide enough tension to prevent it from collapsing and can prolong for a longer duration.

Read more on Negative Tension:What,Why,When,Examples,How To Find.

Compression and Tension Similarities

Both tension and compression are the main forces involved to determine any structure or construction. The presence of both gives better flexibility and durability for any object.

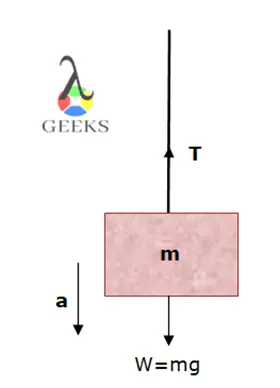
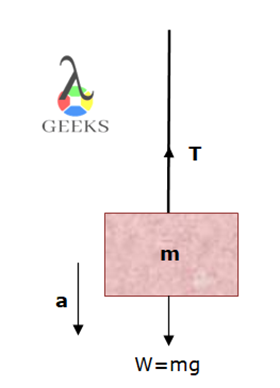
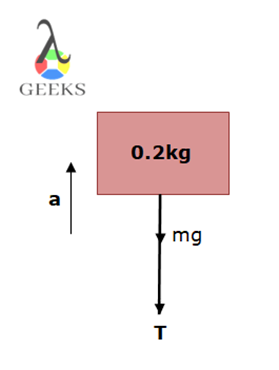
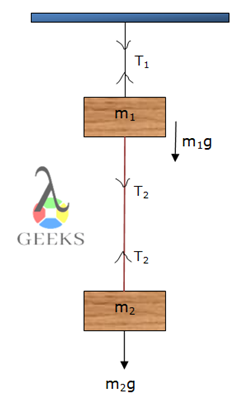
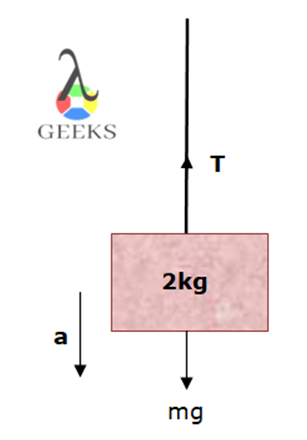
The compression and tension both are measured in the Newton. The tension in the rope due to the weight of mass ‘m’ attached to it in the below diagram is T=m(a+g).

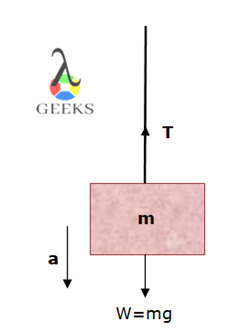
Because the force on the object is F=T-mg and since acceleration is in the negative y-axis direction, we have negative acceleration.

-ma=T-mg

If the acceleration of the object was zero then the tension in the string was just equal to the weight attached to it. That is,

T=mg

SI unit for tension is

T=kg.m/s²=Newton

Compression is also measured in Newton because it’s a force applied on the area and is formulated as

F(c)=ma

Hence, unit for compression is also F(c)=kg.m/s²=Newton.

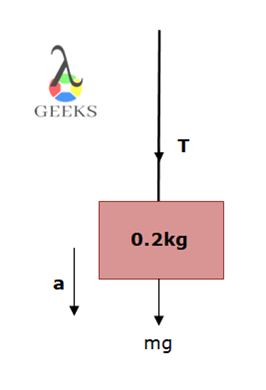
A spring or any elastic object undergoes both tension and compression. A tension is applied that results in the elongation of the object. On compression, the tension is acting downward, although changing the dimensions of the object.

The force due to compressing the elastic object is

F=-T-mg

-ma=-T-mg

As the object accelerates downward in the negative y-axis direction then the acceleration will be taken as negative and hence the negative sign.

Therefore the tension in object is

T=m(a-g)

In this case, the tension will be negative as a<g. This indicates that the negative tension in the object implies compression.

Read more on 15 List of Examples of Tension Force.

What is Better Tension or Compression?

Both, compression as well as tension led to the deformation of the objects. So, we cannot precisely say what is better among each.

If the object is undergoing both compression and tension then it will be better for an object. Because tension acts across the length of the object and acts outwards from the ends well this tensional force is canceled by the compression and hence the object is secured from getting deformed.

There are some materials that can resist the tensional force acting across them, and some materials can withstand compression.

Is Tension a Compressive Force?

Tension is not a compressive force, it is a tensile force.

Tension is opposite to the compression force, as it results in the elongation of the object whereas compression results in the contraction of the object.

Read more on Compression.

Frequently Asked Questions

What is a tension in string tied to the object of mass 5kg accelerating at a speed of 3 m/s²?

Given: m=5kg

a=3 m/s²

The tension in the string is

T=ma=5*3=15N

What will happen if there was no tension in the bridge?

Bridges are made such that they will withstand the heavy load on compression and resist the tension.

The heavy vehicle traveling on a bridge exerts a compression force on the bridge, the bridge would have bent sharply on the application of load on it.

Also Read:

• Tension between two blocks
• Surface tension
• Negative tension

In this article, we will discuss what is negative tension, when it comes into the picture, and how to find it along with examples.

The negative tension comes in the act if the tensional force across the string is less than the weight of the mass attached to it. This is also true, that the tension is acting across the string, making action-reaction pair, so if we consider positive tension in the positive axis then the tension in the opposite direction has to be a negative tension.

What is Negative Tension?

The tension is exerted all across the spring, rope, or strings, and varies depending upon the mass, position, and types of forces experienced on the object attached to it.

If the influence of the tension of the string on the object is less as compared to the weight of the object the string is attached to, that is W>T, then the tension on the string is negative.

Let us understand a valid condition for tension to be negative and how it is different from the other examples. Positive tension is act exactly opposite to the weight of the object attached to it if the object is fixed at a point.

Consider an object of mass ‘m’ attached to a string. A force due to the weight of the mass is acting downward and hence the tension on the string is acting upward across the string.

The net force on the object is

F=T-mg

A force due to weight is acting in a negative y-direction, hence the negative sign.

Now, the acceleration of the object is also in the negative y-direction as the object is accelerating downward.

Hence, we have,

-ma=T-mg

Therefore, the tension in the string is

T=mg-ma

T=m(g-a)

From the above equation, we can say that the tension is negative if a>g. But, this is not a valid case. Let us see further in this article, in which situations we can find negative tension.

Read more on Tension Between Two Blocks: Several Entities And Problem Examples.

When Tension is Negative?

The tension is imposed on the string in the direction opposite to the force acting due to the weight of the object.

The negative tension can be considered as the acceleration of the object due to compression force, a condition where the weight of the object and the tension, both are exerted in the same direction.

The tension will be negative in the following three cases that we are going to discuss below.

Case 1: When a body is accelerating down

Consider an object of mass ‘m’ attached to a string accelerating downward. The tension on the string is also acting in the negative y-axis direction.

The equation of force for the above diagram is

F=-T-mg

-ma=-T-mg

T=m(a-g)

If a<g or a=0,

Then T=-ve or T=-mg

Case 2: When a body is accelerating upward

Consider an object of mass ‘m’ accelerating upward. The tension on the string is also acting downward.

The equation of force for the above diagram is

F=-T-mg

ma=-T-mg

T=-m(a+g)

Here, in this case, the tension is clearly negative.

Case 3: An object in a vertical axis with zero acceleration

Consider an object accelerating in the vertical axis with the help of a rope. The object will experience centripetal force. Let us draw a free-body diagram for it.

The force experienced on the object in a centripetal motion is F=mv²/r which is equal to the tension on the rope if force due to weight is absent.

At a certain point while turning the object is felt heavier, during that time the tension in a rope is equal to the sum of centripetal force acting on the object and the weight of the object. At some point the object feels lighter that is when the tension acts outward, hence the equation of force becomes

F=T+mgSinθ

mv²/r=T+mgSinθ

Hence, the equation for tension becomes,

T=mv²/r-mgSinθ

A tension is negative if v=0 and θ=90⁰, that is the accelerating object stops at 90 degree angle.

Read more on How To Calculate Tension In A String:Exhaustive Insights.

Can Tension be Negative?

A tension is positive when the force is applied to pull the object with the help of a string, or rope.

If instead of pulling, a compressive force is applied, then the tension on the string can be negative. This could also be a case when the strength of the tension on the string is less compared to the weight attached to it.

This is also categorized as the compression force on the string. But string or rope can’t be compressed; only the spring can be compressed. Hence, on the application of the compressive force, the tension on the spring is negative.

Read more on Is tension a conservative force: Exhaustive Insight.

How to Find Negative Tension?

Negative tension is simply a compression force and acts always in the direction of the weight of the object.

The negative tension in the spring can be calculated by measuring the net force imposed on the object and then finding the acceleration of the object due to force.

Let us understand how to calculate the negative tension by solving the problem given below.

Problem: An object of mass 200 grams attached to a spring is compressed due to which the acceleration of the object is found to be 1m/s. Find the tension in the string.

Given: m=200 grams = 0.2kg

a=1m/s

g=9.8m/s²

Let us first draw a free-body diagram for the same.

Now, write the equation of force.

F=-T-mg

The acceleration of the object is in the negative y-axis plane, hence

-ma=-T-mg

Therefore, the tension on the spring is equal to

T=ma-mg

T=m(a-g)

Now, substitute the given values

T=0.2kg*(1-9.8)m/s²

T=0.2kg*(-8.8)m/s²

T=-1.76N

The tension on the sprig is -1.76N.

Read more on How To Find Normal Force With Tension: Several Approaches and Problem Examples.

Negative Tension Examples

There are various examples of the negative tension that we often come across. Let us ponder upon some examples.

Drowning of Bolt in the Water

Consider a bolt tied to a tread dropped in a glass of water. The molecular density of the bolt is more than the water, the bolt will immerse in the water accelerating down to the bottom of the glass.

If we write the equation of force for tension, then we have

F=-T-mg

T=-F-mg

The acceleration of the bolt is downward, hence,

T=-(-ma)-mg

T=m(a-g)

If the mass of the bolt is 4 grams, and the acceleration is 0.03m/s², then tension on the tread is

T=4*10^-3kg* (0.03-9.8)m/s²

T=4*10^-3kg* (-9.77)m/s²

T=-0.039N

The tension on the tread is -0.039 Newton.

Lantern Hanging on the Hook with String Suddenly Detach and Falls Down

When the string detached from the lantern, the weight of the lantern is larger than the tension across the string, and hence the lantern accelerates downward.

Spring Shoes or Jumping Shoes

These shoes come with a spring attached beneath the shoes or a bouncer. When the body weight falls on the shoe it compresses. This time the body accelerates little downward, and the tension applied on the spring is also acting downward. Well, due to the potential energy accumulation in the spring and because of its elastic nature it regains its shape. That is why the spring is used in shoes to jump higher.

A Ladder on the Helicopter

Imagine that there is no person standing on the latter and the helicopter is accelerating in the upward direction. The tension may be applicable to the latter due to the air resistance. Well, the acceleration is upward and the tension is in the negative direction.

The mass m=0, hence the equation of force will be

F=-T

That is T=-ma.

Skipping

Tension on a massless rope is always zero. Because the tension on one end of the rope is canceled out by the equal and opposite tension from the other end. While skipping, the tension is exerted across the rope, but it is not positive because no pulling force is applied on the rope. The rope undergoes air resistance and the tension is created in the rope due to centrifugal force.

Loosening a Guitar strings

The tension on the strings on the guitar is created to generate the sound by bending the string or strumming it. If we loosen the string, then the tension on the string will be negative.

Balloon Floating in the Air

A balloon is filled with helium gas which is very light and hence freely floats to rise above the air. The density of helium is very less compared to the air molecules.

The balloon experiences a buoy force that carries it in the upward direction. The net force on the balloon is given by the equation

F_buoy=ρ vg=-T-mg

Hence, tension is equal to

T=-ρvg-mg

T=-(ρ v+m)g

The tension on the tread of the balloon is negative.

Read more on Tension.

Frequently Asked Questions

Is stress a negative tension?

Stress is applied in such a way that it results in pulling two objects apart from each other, and it is called tensional stress.

Tensional stress is exerted in two opposite directions, separating or pulling the objects away from each other. If the tension is acting on the x-axis, then the tension in the left hand side is a negative tension.

Why compression is a negative tension?

The force applied to reduce the volume or size of the object is called compression.

On compression the tension is acting in the negative y-direction along with the weight of the object, then acceleration could be in positive or negative axis, the tension is always negative.

Also Read:

• Tension vs compression
• Surface tension
• Tension between two blocks

Dive into our example-rich guide on Tension Between Two Blocks, simplifying this key concept in physics for easy understanding

The tensional force acting on the string is not the same for all objects; it depends upon the mass and the acceleration of the object, and the force. Let us see how to find the tension between two blocks.

How to Find Tension between Two Blocks?

It is a force defined for strings, rope, or springs; tread like objects which experience tension on stretching.

The tension between two blocks can be found by knowing the net forces acting on the two blocks attached to the string, we can calculate the tension exerted on the string due to the two blocks.

Read more on 15 List of Examples of Tension Force.

Problem: Consider two blocks of masses ‘m₁’ and ‘m₂’ attached to a rope and suspended freely in the air. Calculate the tension imposed on the rope due to two blocks.

Solution: The tension felt on the rope is due to the blocks hanging on it, and relies upon the masses of the blocks.

Step1: Draw a free-body diagram for any problem

To calculate the tension on the rope, first draw the free body diagram understanding the problem, explaining the net forces acting on the blocks. Here, is a free body diagram of the two blocks for the above problem.

The diagram above gives us a rough idea of the tension generated in the rope due to two blocks. The tension T₁ is due to the mass ‘m₁’ and tension T₂ is exerted due to the mass ‘m₂’. The tension is felt across the length of the rope and in both the direction, in the positive y-axis and in the negative y-axis direction. The force due to gravity is acting downward due to both the weights is clearly indicated in the free-body diagram.

Step 2: Write the equation for net forces acting on each block.

The net force acting on the mass ‘m₂’ is the tensional force and the force due to gravity acting downward in the negative y-direction. So, we have the equation as below,

F=T₂-m₂g

m₂a=T₂-m₂g —-(1)

The net force acting on the mass ‘m₁’ is the tensional force and weight acting downward in the negative y-direction. So, we can write the equation as,

F=T₁ – T₂ – m₁g

m₁a=T₁ – T₂ – m₁g —(2)

Step 3: Frame the equation to find the net acceleration of the blocks.

The mass ‘m₂’ is fixed and is not accelerating, hence a=0. Therefore we can write Eqn(1) as,

T₂ – m₂g=0—(3)

The mass ‘m₁’ is also fixed at a point and is not accelerating, hence a=0. Therefore from Eqn(2), we have,

T₁-T₂-m₂g=0 —(4)

It doesn’t mean that if there is no acceleration in the rope then there is no tension in the rope, this is evident from the above equation that there is a tension exerting in the rope due to each block. Let us see further how to find this tension in the rope.

Step 4: Calculate the total tension on the rope

From the Eqn(3), we have

T₂ = m₂g

The tension T₂ is applicable due to mass ‘m₂’ and the acceleration due to gravity, which is equal to the weight of block 2.

From eqn (4) we have,

T₁ = T₂ + m₂g

Substituting the value to T₂, we now have,

T₁ = m₁g + m₂g

So, T₁=g(m₂+m₁)

The tension T₁ is due to the total mass attached to the string, as the rope exerting tension T₁ is exerting weight of both the blocks.

Step 5: Find the net tension experiencing on the rope

The net tension is the sum of all the tensions exerted on the rope. Hence, net tension T is equal to the addition of T₁ and T₂,

T=T₁+T₂

T=g(m₂+m₁)+m₂g

T=m₁g+2m₂g

T=(m₁+2m₂)g

This is a net tension in the rope due to two blocks suspended vertically above the ground.

Tension between Two Blocks on an Incline

Now, that we know how to calculate the tension between two blocks in a vertical direction, let us also ponder upon how to measure tension between the two blocks on an inclined slope.

Read more on How to calculate tension force: Exhaustive Insight.

Problem: Consider two blocks of masses 30kg and 45kg inclined on the slope attached to string on a pulley. The inclination angle of the slope on which mass of block ‘m₁’ lies is at angle 30⁰, and the slope on which mass ‘m₂’ relies is inclined at an angle 45⁰. Calculate the tension exerted on a string.

Solution: First, let us draw a free-body diagram of the two blocks inclined on the plane of different angles.

Now, write the equation for forces exerting on the blocks. The net force exerted on each body is the additional forces due to weight, gravity, the normal force which acts opposite to the weight of the body, and the tensional force exerted across the string.

The forces acting on mass m₁ are in 2 directions, in the x-direction is, m₁a=-m₁gSin30⁰+T, minus sign is because the force is acting in the negative x-axis; and in the y-direction is m₁a=-m₁gCos300+N.

The forces acting on mass m₂ are, in the x-direction is, m₂a=m₂gSin45⁰-T

The tension is exerted in the negative x-axis.

And, in the y-direction is m₂a=-m₂gcos45⁰+ N

The tension comes into existence in the x-direction; hence we will consider 2 equations,

m₁a=-m₁gSin30°+T

m₂a=m₂gSin45°-T

Adding these two equations, we have,

m₁a + m₂a=m₂gSin45°-T – m₁gSin30°+T

Let us calculate acceleration of the blocks, so let’s substitute the value given.

(30+45)a=9.8* (45*1/√2)-30* (1/2)

75a=9.8* (22.5√2-15)

75a=9.8*(31.82-15)

a=9.8*16.82/75

a=2.2 m/s²

Now, we know the acceleration of the blocks. Substituting this in any of the above equations we can find the tension in the rope due to two blocks.

Consider the equation, m₁a=-m₁gSin30°+T

T=m₁a+m₁gSin30°

T=m₁(a+gSin30°)

=30* (2.2+9.8*1/2)

=30* (2.2+4.9)

=30*7.1=213N

Hence, the tension in the rope is 213N.

Read more on How To Calculate Tension In A String:Exhaustive Insights.

Find Tension between Two Blocks on Horizontal Surface

The tension between the blocks placed on a horizontal surface comes into the picture when the pulling force is applied to one of the blocks. On pushing the object closer to each other or away from the other, the tension will be absent in the string joining the both.

Read more on Tension Force.

Problem: Consider two-block kept on a frictionless plane having mass m₁=3kg and m₂= 5kg. Both these masses are tied with a string, and a mass of 5kg is pulled in the positive x-direction applying a force of 230N. Measure the tension exerted on the string.

Solution: Let us draw a free body diagram considering the above situation,

The tension acting on block 1 is equal to the force due to acceleration, given by the equation,

T=m₁a=3a

The force applied on the block 2 is

F=T+m₂a

Tension due to block 2 is

T=F-m₂a

If we know the acceleration of the block, then it is easy to calculate the tensional force.

The net force applied on the blocks is

F= (m₁+m₂)a

Hence,a=F/m₁+m₂

From this, we can write the first equation as

T=3F/m₁+m₂

Hence, the tension exerted on the string is

T=3* 230/3+5

=3*230/8=86.25N

Tension of 86.25N is applied across the string.

Read more on Is tension a conservative force: Exhaustive Insight.

Frequently Asked Questions

A body of mass 2kg is attached to the string and is accelerating downward at a rate of 3m/s. What is tension on the string?

Given: m=2kg

a=3m/s

The force acting on the object is

F=T-mg

Since the acceleration of the body is downward F=-ma,

-ma=T-mg

T=m(g-a)

=2* (9.8-3)

=2*6.8=13.6N

The tension on a string is 13.6N.

What is a tension Force?

The force acting on every object is categorized depending upon the shape and size of the object and the direction of the force.

The tensional force is a contact force and acts on pulling the objects. The force acting across the length of the rope, strings, or springs is called the tension force.

Also Read:

• Negative tension
• Tension vs compression
• Surface tension