Mass

Mastering the Measurement of Gravitational Energy Effects Near Massive Celestial Bodies

by
how to measure gravitational energy effects near massive celestial bodies

Summary Exploring the intricate interplay between gravity and energy is crucial for understanding the dynamics of massive celestial bodies. This comprehensive guide delves into the key concepts, formulas, and practical applications for measuring gravitational energy effects near these colossal entities. From calculating gravitational potential energy and escape velocity to analyzing kinetic energy and total energy, … Read more

How To Find Mass In Centripetal Force: Problem And Examples

by
mass in centripetal force 0

Centripetal force is a fundamental concept in physics that describes the force required to keep an object moving in a circular path. It is essential to understand how to calculate centripetal force, as well as how to determine the mass of an object using centripetal force. In this blog post, we will explore step-by-step guides and examples for both scenarios.

How to Calculate Centripetal Force with Known Mass and Acceleration

The Formula for Calculating Centripetal Force

mass in centripetal force 3

To calculate centripetal force, we use the following formula:

F_c = frac{m cdot v^2}{r}

Where:
– F_c is the centripetal force in Newtons (N)
– m is the mass of the object in kilograms (kg)
– v is the velocity of the object in meters per second (m/s)
– r is the radius of the circular path in meters (m)

Step-by-Step Guide to Calculate Centripetal Force

how to find mass in centripetal force
Image by Cdang – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

To calculate centripetal force, follow these steps:

  1. Determine the mass of the object (m) in kilograms (kg).
  2. Measure the velocity of the object (v) in meters per second (m/s).
  3. Measure the radius of the circular path (r) in meters (m).
  4. Substitute the values of mass, velocity, and radius into the centripetal force formula F_c = frac{m cdot v^2}{r}.
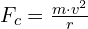  5. Calculate the centripetal force (Fc) using the formula.

Worked Out Example: Calculating Centripetal Force with Known Mass and Acceleration

Let’s work through an example to solidify our understanding. Suppose we have a mass (m) of 2 kg, a velocity (v) of 5 m/s, and a radius (r) of 3 meters. We can calculate the centripetal force (Fc) using the following steps:

  1. Mass (m) = 2 kg
  2. Velocity (v) = 5 m/s
  3. Radius (r) = 3 meters

Substituting these values into the centripetal force formula F_c = frac{m cdot v^2}{r}, we can calculate:

F_c = frac{2 cdot (5^2)}{3}
F_c = frac{2 cdot 25}{3}
F_c = frac{50}{3}
F_c approx 16.67 , text{N}

Therefore, the centripetal force required to keep the object moving in a circular path is approximately 16.67 Newtons (N).

How to Determine Mass Using Centripetal Force

The Formula for Finding Mass in Centripetal Force

To determine the mass of an object using centripetal force, rearrange the centripetal force formula as follows:

m = frac{F_c cdot r}{v^2}

Where:
– m is the mass of the object in kilograms (kg)
– F_c is the centripetal force in Newtons (N)
– r is the radius of the circular path in meters (m)
– v is the velocity of the object in meters per second (m/s)

Step-by-Step Guide to Find Mass Using Centripetal Force

To find the mass using centripetal force, follow these steps:

  1. Determine the centripetal force (Fc) in Newtons (N).
  2. Measure the radius of the circular path (r) in meters (m).
  3. Measure the velocity of the object (v) in meters per second (m/s).
  4. Substitute the values of centripetal force, radius, and velocity into the mass formula m = frac{F_c cdot r}{v^2}.
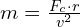  5. Calculate the mass (m) using the formula.

Worked Out Example: Finding Mass Using Centripetal Force

Let’s work through an example to illustrate how to find mass using centripetal force. Suppose we have a centripetal force (Fc) of 30 N, a radius (r) of 4 meters, and a velocity (v) of 6 m/s. We can determine the mass (m) using the following steps:

  1. Centripetal force (Fc) = 30 N
  2. Radius (r) = 4 meters
  3. Velocity (v) = 6 m/s

Substituting these values into the mass formula m = frac{F_c cdot r}{v^2}, we can calculate:

m = frac{30 cdot 4}{6^2}
m = frac{120}{36}
m approx 3.33 , text{kg}

Therefore, the mass of the object is approximately 3.33 kilograms (kg) based on the given centripetal force, radius, and velocity.

How to Calculate Centripetal Force without Known Mass

mass in centripetal force 1

The Concept of Centripetal Force without Mass

In some situations, we may need to calculate the centripetal force without knowing the mass of the object. This can be achieved by using Newton’s second law of motion, which states that the force acting on an object is equal to its mass multiplied by its acceleration. Since centripetal force is responsible for the acceleration of an object moving in a circular path, we can use this concept to calculate the centripetal force without known mass.

Step-by-Step Guide to Calculate Centripetal Force without Known Mass

mass in centripetal force 2

To calculate centripetal force without known mass, follow these steps:

  1. Determine the acceleration of the object (a) in meters per second squared (m/s^2).
  2. Measure the radius of the circular path (r) in meters (m).
  3. Substitute the values of acceleration and radius into the formula F_c = m cdot a.
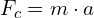  4. Calculate the centripetal force (Fc) using the formula.

Worked Out Example: Calculating Centripetal Force without Known Mass

Let’s work through an example to illustrate how to calculate centripetal force without known mass. Suppose we have an acceleration (a) of 10 m/s^2 and a radius (r) of 2 meters. We can calculate the centripetal force (Fc) using the following steps:

  1. Acceleration (a) = 10 m/s^2
  2. Radius (r) = 2 meters

Substituting these values into the centripetal force formula F_c = m cdot a, we can calculate:

F_c = m cdot 10

Since we don’t know the mass (m), we cannot obtain an exact value for the centripetal force. However, we can conclude that the centripetal force is proportional to the acceleration of the object and inversely proportional to the radius of the circular path.

By understanding how to calculate centripetal force with known mass and acceleration, determine mass using centripetal force, and calculate centripetal force without known mass, we can better comprehend the concept of centripetal force and its significance in physics. These formulas and step-by-step guides provide a solid foundation for solving various problems related to centripetal force, allowing us to analyze the motion of objects in circular paths with ease.

Keep practicing and exploring the applications of centripetal force in different scenarios to develop a deeper understanding of this fundamental concept in physics.

How can mass be determined using centripetal force and how does it relate to calculating constant acceleration using distance and time?

The concept of finding mass in centripetal force involves understanding the relationship between force, mass, and centripetal acceleration. On the other hand, the idea of “calculating constant acceleration using distance” explores how to determine constant acceleration based on distance and time measurements. By combining these themes, we can investigate how the mass of an object impacts its constant acceleration and utilize the relationship between centripetal force and constant acceleration to determine the mass of an object when given its distance and time measurements.

Numerical Problems on How to Find Mass in Centripetal Force

Problem 1:

how to find mass in centripetal force
Image by Cleontuni – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 3.0.

A car of mass 1200 kg is moving in a circular path with a radius of 40 m. If the car is experiencing a centripetal force of 1000 N, what is the speed of the car?

Solution:

Given:
– Mass of the car, m = 1200 kg
– Radius of the circular path, r = 40 m
– Centripetal force, F = 1000 N

We know that the centripetal force (F) is given by the equation:

F = frac{{mv^2}}{r}

where:
– m is the mass of the object
– v is the velocity of the object
– r is the radius of the circular path

To find the velocity (v), we rearrange the equation:

v = sqrt{frac{{Fr}}{m}}

Substituting the given values:

v = sqrt{frac{{1000 , text{N} times 40 , text{m}}}{1200 , text{kg}}}

Simplifying the equation:

v = sqrt{frac{40000 , text{N} cdot text{m}}{1200 , text{kg}}}

v = sqrt{33.33 , text{m}^2/text{s}^2}

Therefore, the speed of the car is approximately 5.77 m/s.

Problem 2:

A stone of mass 0.2 kg is tied to a string and is swung in a circular path of radius 0.5 m. If the stone completes one revolution in 2 seconds, what is the tension in the string?

Solution:

Given:
– Mass of the stone, m = 0.2 kg
– Radius of the circular path, r = 0.5 m
– Time taken for one revolution, T = 2 s

The period (T) of one revolution is the time taken for the stone to complete one full cycle. It is related to the frequency (f) using the equation:

T = frac{1}{f}

We can find the frequency using:

f = frac{1}{T}

Substituting the given values:

f = frac{1}{2 , text{s}}

f = 0.5 , text{Hz}

The centripetal force (F) acting on the stone is given by the equation:

F = frac{mv^2}{r}

where:
– m is the mass of the object
– v is the velocity of the object
– r is the radius of the circular path

We can find the velocity (v) using:

v = 2pi rf

Substituting the given values:

v = 2pi times 0.5 , text{m} times 0.5 , text{Hz}

v = pi , text{m/s}

Substituting the values of m, v, and r into the equation for centripetal force:

F = frac{0.2 , text{kg} times (pi , text{m/s})^2}{0.5 , text{m}}

Simplifying the equation:

F = 2pi^2 , text{N}

Therefore, the tension in the string is approximately 19.74 N.

Problem 3:

A satellite of mass 500 kg is in orbit around the Earth at a radius of 6.4 x 10^6 m. If the satellite is experiencing a centripetal force of 2 x 10^7 N, what is the speed of the satellite?

Solution:

Given:
– Mass of the satellite, m = 500 kg
– Radius of the orbit, r = 6.4 x 10^6 m
– Centripetal force, F = 2 x 10^7 N

Using the same equation as in Problem 1, we can find the velocity (v) by rearranging the equation:

v = sqrt{frac{{Fr}}{m}}

Substituting the given values:

v = sqrt{frac{{2 times 10^7 , text{N} times (6.4 times 10^6 , text{m})}}{500 , text{kg}}}

Simplifying the equation:

v = sqrt{frac{{128 times 10^{13} , text{N} cdot text{m}}}{500 , text{kg}}}

v = sqrt{256 times 10^{11} , text{m}^2/text{s}^2}

Therefore, the speed of the satellite is approximately 1.6 x 10^6 m/s.

Also Read:

Mastering Kinetic Energy: A Comprehensive Guide to Finding It Using Speed and Mass

by
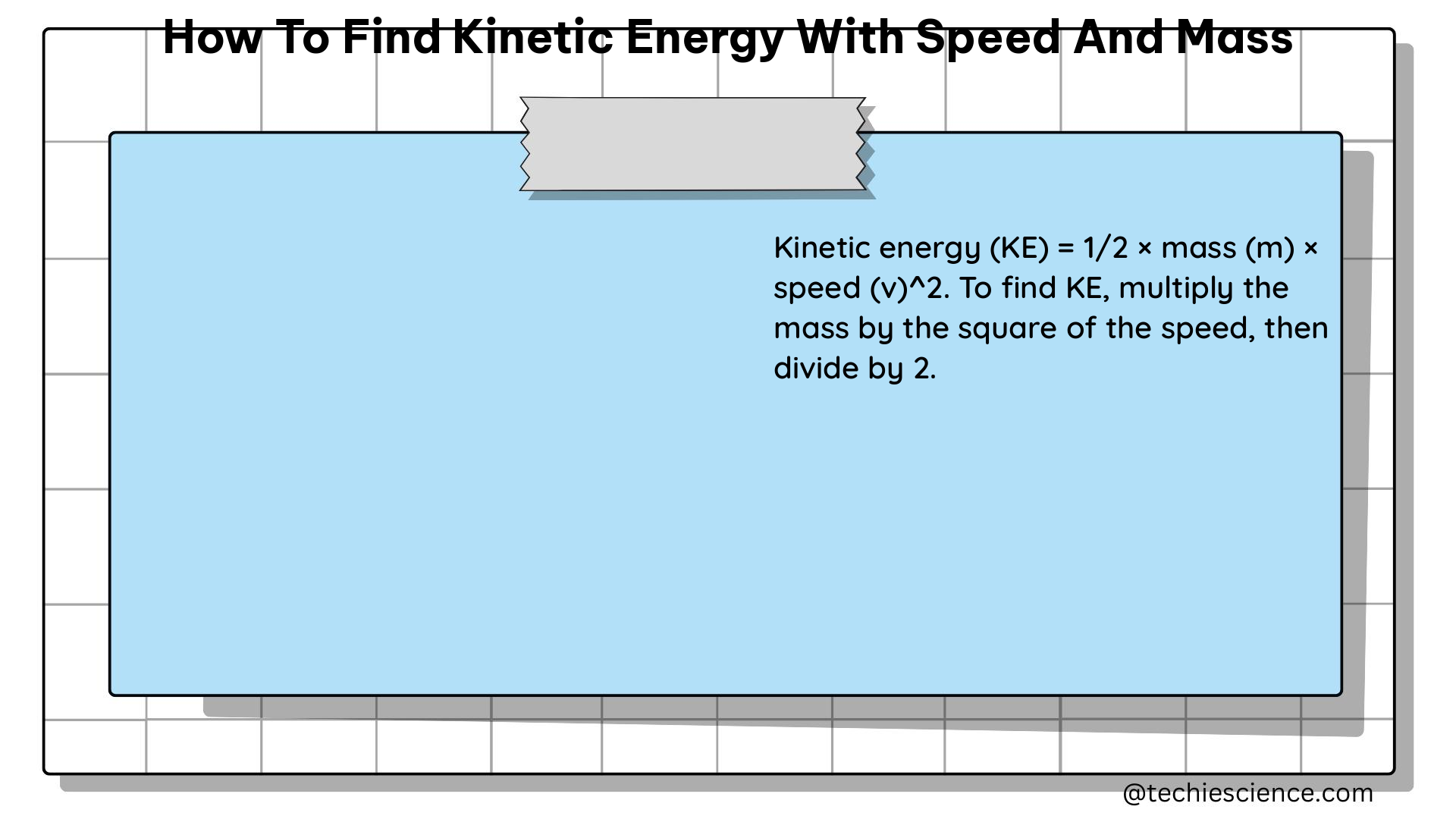
how to find kinetic energy with speed and mass

Kinetic energy is a fundamental concept in physics that describes the energy an object possesses due to its motion. Determining the kinetic energy of an object is crucial in various fields, from engineering and transportation to sports and everyday life. In this comprehensive guide, we will delve into the intricacies of calculating kinetic energy using … Read more

How to Find Net Force with Mass and Speed: Various Methods, Problems and Facts

by
net force with mass and speed 0

How to Find Net Force with Mass and Speed

In physics, understanding the concept of net force and how it relates to mass and speed is crucial. Net force refers to the overall force acting on an object, taking into account both magnitude and direction. By considering mass and speed, we can calculate the net force acting on an object and gain insights into its motion. Let’s dive deeper into the details of how to find net force with mass and speed.

Understanding the Basic Concepts

1. Definition of Net Force

Net force is the vector sum of all the forces acting on an object. A force can be defined as a push or pull that can cause an object to accelerate or change its motion. When multiple forces act on an object, their combined effect is the net force. The net force determines the object’s acceleration and subsequent movement.

2. Understanding Mass in Physics

In physics, mass is a measure of an object’s resistance to acceleration. It quantifies the amount of matter in an object. Mass is a scalar quantity and is typically measured in kilograms (kg). According to Newton’s second law of motion, the net force acting on an object is directly proportional to its mass. This means that as the mass of an object increases, the net force required to accelerate it also increases.

3. The Role of Speed in Calculating Net Force

Speed, on the other hand, refers to the rate at which an object covers distance. It is a scalar quantity and is typically measured in meters per second (m/s). While speed alone does not affect net force, it influences the momentum of an object. Momentum is the product of an object’s mass and velocity and is given by the equation:

text{Momentum} = text{Mass} times text{Velocity}

The Relationship between Net Force, Mass, and Speed

1. The Direct Proportionality of Force and Mass

According to Newton’s second law of motion, the net force acting on an object is directly proportional to its mass and acceleration. Mathematically, this can be expressed as:

text{Net Force} = text{Mass} times text{Acceleration}

This equation highlights that the net force acting on an object is directly proportional to its mass. As the mass of an object increases, a greater net force is required to accelerate it. Conversely, if the mass decreases, less net force is needed to produce the same acceleration.

2. The Impact of Speed on Net Force

While speed does not directly affect net force, it influences the kinetic energy of an object. Kinetic energy is the energy possessed by an object due to its motion and is given by the equation:

text{Kinetic Energy} = frac{1}{2} times text{Mass} times text{Velocity}^2

Since kinetic energy is directly proportional to the square of the velocity, an increase in speed results in a larger kinetic energy. This, in turn, can affect the net force required to bring about changes in an object’s motion.

The Mathematical Approach to Finding Net Force

1. The Formula for Calculating Net Force

To calculate the net force acting on an object, we can use the equation:

text{Net Force} = text{Mass} times text{Acceleration}

This formula allows us to determine the net force when the mass and acceleration of an object are known. By substituting the appropriate values, we can find the net force and understand how it impacts the object’s motion.

2. The Importance of Units in Calculations

When calculating net force, it is crucial to ensure that the units of mass, acceleration, and net force are consistent. For example, if the mass is given in kilograms (kg) and the acceleration in meters per second squared (m/s^2), the resulting net force will be in Newtons (N). Maintaining consistent units is essential for accurate calculations and meaningful interpretations of the results.

3. Worked Out Examples of Net Force Calculations

Let’s consider a couple of examples to illustrate how to find net force using mass and speed.

Example 1:
A car with a mass of 1000 kg is accelerating at a rate of 5 m/s^2. What is the net force acting on the car?

Using the equation text{Net Force} = text{Mass} times text{Acceleration} , we can substitute the given values:

text{Net Force} = 1000 , text{kg} times 5 , text{m/s}^2 = 5000 , text{N}

Therefore, the net force acting on the car is 5000 Newtons.

Example 2:
A tennis ball with a mass of 0.1 kg is hit with a speed of 20 m/s. What is the net force acting on the ball?

Since we are given the mass and speed, we can calculate the kinetic energy using the equation:

text{Kinetic Energy} = frac{1}{2} times text{Mass} times text{Velocity}^2

text{Kinetic Energy} = frac{1}{2} times 0.1 , text{kg} times (20 , text{m/s})^2 = 20 , text{J}

The kinetic energy of the tennis ball is 20 Joules. While this information alone does not provide the net force, it illustrates how speed influences the kinetic energy of an object.

Misconceptions and Common Errors in Calculating Net Force

net force with mass and speed 3

Misconception about the Role of Mass and Speed

A common misconception is that net force is solely determined by an object’s mass or speed. However, net force depends on both mass and acceleration. While speed affects other factors like kinetic energy, it does not directly determine net force.

Common Calculation Errors

When calculating net force, there are a few common errors to watch out for. These include incorrect unit conversions, using the wrong formula, and miscalculating values. It is essential to double-check calculations and review the given information to avoid these errors.

Tips to Avoid These Errors

To ensure accurate net force calculations, consider the following tips:
– Carefully read the problem and identify the given information.
– Convert units to ensure consistency.
– Use the appropriate formula for net force calculations.
– Double-check calculations and review the solution for reasonableness.

The Role of Acceleration in Net Force Calculations

Understanding Acceleration

Acceleration is the rate at which an object’s velocity changes with time. It is a vector quantity and is typically measured in meters per second squared (m/s^2). Acceleration can be positive or negative, depending on whether the object is speeding up or slowing down. The net force acting on an object is directly proportional to its acceleration, as stated by Newton’s second law.

The Relationship between Acceleration, Mass, and Net Force

According to Newton’s second law of motion, the net force acting on an object is equal to the product of its mass and acceleration. Mathematically, this relationship can be expressed as:

text{Net Force} = text{Mass} times text{Acceleration}

By understanding this relationship, we can determine the net force acting on an object when its mass and acceleration are known.

How to Incorporate Acceleration in Net Force Calculations

To incorporate acceleration in net force calculations, follow these steps:
1. Identify the mass and acceleration values given in the problem.
2. Use the equation text{Net Force} = text{Mass} times text{Acceleration} to calculate the net force.
3. Substitute the given values into the equation and solve for the net force.

Advanced Concepts Related to Net Force

net force with mass and speed 2

The Concept of Constant Speed and Constant Velocity

While speed refers to the rate at which an object covers distance, velocity includes both speed and direction. When an object moves at constant speed in a straight line, the net force acting on it is zero. This is because the forces acting on the object are balanced, resulting in no net force and no acceleration. However, if the object changes its speed or direction, the net force is no longer zero.

The Role of Distance in Net Force Calculations

The distance an object travels is not directly related to net force calculations. Net force primarily depends on mass, acceleration, and velocity. However, the distance an object travels can indirectly affect the net force by influencing the time it takes to cover that distance. Time, in turn, can impact the acceleration, and consequently, the net force required for an object to reach a certain speed or change its motion.

The Impact of Time on Net Force Calculations

Time plays a role in net force calculations by affecting the acceleration of an object. Acceleration is the rate at which velocity changes over time. By considering how long it takes for an object to reach a certain speed or change its motion, we can assess the magnitude of the net force required. It is important to note that time alone does not determine net force but influences the rate of change in velocity.

Practical Applications of Net Force Calculations

Real-life Scenarios where Net Force Calculations are Used

Net force calculations have practical applications in various fields, including physics and engineering. Some examples include:
– Calculating the forces acting on a moving vehicle to ensure it remains stable and safe.
– Determining the forces required for an object to accelerate or decelerate in industrial machinery.
– Analyzing the forces acting on structures, such as bridges or buildings, to ensure their stability.

The Importance of Net Force Calculations in Physics and Engineering

Understanding net force and its relationship with mass and speed is crucial in physics and engineering. It allows us to analyze and predict how objects will move and interact with their surroundings. By calculating net force, engineers can design structures and machines that operate safely and efficiently. Physicists can study the fundamental laws of nature and make meaningful observations about the universe.

By grasping the principles of net force, mass, and speed, we can better comprehend the forces at play in our world. Whether it’s a moving car, a rocket launching into space, or a structure standing tall, net force calculations provide us with insights into how objects behave and interact with their environment.

Remember, practice and application are key to mastering the calculation of net force. So keep exploring, solving problems, and discovering the fascinating world of physics!

What are the steps to calculate net force and how does it relate to mass and speed?

Net force is the vector sum of all the forces acting on an object. To calculate net force, you need to consider both magnitude and direction of individual forces. By using the formula F = m * a, where F is the force, m is the mass, and a is the acceleration, you can find the net force. The mass of an object affects the net force as a greater mass requires a larger force to cause the same acceleration. Similarly, speed also plays a role in net force, as a faster object will experience greater forces due to the effect of inertia. To dive deeper into these concepts and learn how to calculate net force more extensively, you can refer to the article on How to Calculate Net Force.

Numerical Problems on how to find net force with mass and speed

Problem 1:

net force with mass and speed 1

A car of mass 1000 kg is traveling at a speed of 20 m/s. Calculate the net force acting on the car.

Solution:
Given:
Mass of the car, m = 1000 , text{kg}
Speed of the car, v = 20 , text{m/s}

The formula to find net force is:

F_{text{net}} = m cdot a

where
F_{text{net}} = Net force
m = Mass
a = Acceleration

Since we are given the mass and speed, we need to find the acceleration first. We can use the formula:

a = frac{{Delta v}}{{Delta t}}

where
Delta v = Change in velocity
Delta t = Change in time

As the car is traveling at a constant speed, the change in velocity is zero. Therefore, the acceleration is also zero.

Substituting the values in the formula for net force:

F_{text{net}} = 1000 , text{kg} cdot 0 , text{m/s}^2

Simplifying the expression, we find:

F_{text{net}} = 0 , text{N}

Hence, the net force acting on the car is 0 N.

Problem 2:

A rocket of mass 5000 kg is accelerating at a rate of 8 , text{m/s}^2. Calculate the net force acting on the rocket.

Solution:
Given:
Mass of the rocket, m = 5000 , text{kg}
Acceleration of the rocket, a = 8 , text{m/s}^2

Using the formula for net force:

F_{text{net}} = m cdot a

Substituting the given values:

F_{text{net}} = 5000 , text{kg} cdot 8 , text{m/s}^2

Evaluating the expression, we find:

F_{text{net}} = 40000 , text{N}

Hence, the net force acting on the rocket is 40000 N.

Problem 3:

A cyclist of mass 75 kg is traveling at a speed of 10 , text{m/s}. The cyclist applies a force of 500 N in the forward direction. Calculate the net force acting on the cyclist.

Solution:
Given:
Mass of the cyclist, m = 75 , text{kg}
Speed of the cyclist, v = 10 , text{m/s}
Applied force, F_{text{applied}} = 500 , text{N}

To calculate the net force, we need to consider both the applied force and the force of friction.

The formula to find net force is:

F_{text{net}} = F_{text{applied}} - F_{text{friction}}

where
F_{text{net}} = Net force
F_{text{applied}} = Applied force
F_{text{friction}} = Force of friction

The force of friction can be calculated using the formula:

F_{text{friction}} = mu cdot F_{text{normal}}

where
mu = Coefficient of friction
F_{text{normal}} = Normal force

Since the cyclist is moving horizontally with a constant speed, the normal force is equal to the gravitational force acting on the cyclist:

F_{text{normal}} = m cdot g

where
g = Acceleration due to gravity (9.8 , text{m/s}^2)

Substituting the values:

F_{text{normal}} = 75 , text{kg} cdot 9.8 , text{m/s}^2

Evaluating the expression, we find:

F_{text{normal}} = 735 , text{N}

Now, we can calculate the force of friction:

F_{text{friction}} = mu cdot F_{text{normal}}

Substituting the given coefficient of friction:

F_{text{friction}} = 0.2 cdot 735 , text{N}

Evaluating the expression, we find:

F_{text{friction}} = 147 , text{N}

Finally, we can calculate the net force:

F_{text{net}} = F_{text{applied}} - F_{text{friction}}

Substituting the given applied force:

F_{text{net}} = 500 , text{N} - 147 , text{N}

Evaluating the expression, we find:

F_{text{net}} = 353 , text{N}

Hence, the net force acting on the cyclist is 353 N.

Also Read:

Does Mass Affect Potential Energy:Detailed Facts,Examples And FAQs

by

Does mass affect potential energy of an object? Before answering this question, we know that Potential energy can be affected by various things, including the mass of the object.

The mass has a direct relation with inertia, which is one reason for gaining or losing potential energy. The contribution of mass on the potential energy, how does mass affect potential energy, and what factors are responsible for the mass to influence the potential energy are discussed in detail in this post.

How does mass affect the potential energy

Consider a car, and a shot put is placed at the top of a hill. Does mass affect potential energy of the car and shot put? How? Which among them has more potential energy?

It isn’t easy to answer because both are at the same height. But by this question, we get a clear picture of how mass affects potential energy.

Generally, the mass of the car is more compared to the shot put. So that car needs an external force to trigger the motion. For any object, the stored potential energy is needed to trigger the first move. The car begins to move by converting its potential energy into work.

Since the mass of the car is more, the car has a lot of stored potential energy, which is responsible for the motion of the car. The work now has a new form of energy called kinetic energy.

does mass affect potential energy
Illustration to show how does mass affect potential energy

The shot put also has the potential energy that causes the motion, but it is comparatively less than the car because the mass of the shot put is less.

The effect of mass on potential energy can also be explained in terms of inertia since inertia is only due to mass.

If an object has more mass, the inertia acting on the body is more as the mass directly influences the inertia. This inertia makes the object possess more potential energy.

Consider a weight lifter is trying to lift the heavyweights. Since the mass of the weights is more than his body weight, he requires more energy to lift it.

The energy that a weight lifter needs to lift is nothing but potential energy. The lifter has more potential energy, which is transferred to the weights. Thus the body possesses more potential energy if it has more mass.

How does mass affect gravitational potential energy

The gravitational potential energy is largely influenced by the mass of the object.

By the formula of gravitational potential energy, given as

PE = m* g* h

The mass is directly corresponding to the potential energy. Thus increase in the mass makes the object possess more potential energy.

Consider the example of a rocket launch. The mass of the rocket is more; hence it requires a large amount of fuel to take off and escape from the earth’s gravitational pull. This implies that the rocket possesses more potential energy, so it requires a more external force to launch. As the fuel is burnt, the stored potential energy helps the rocket to take off by converting itself into kinetic energy.

How does doubling mass affect potential energy

Consider that an object of mass ‘m’ has the potential energy ‘PE’ and is ready to work. If another object of the same mass ‘m’ is attached to the first object, i.e., the total system has doubled mass as ‘2m’, does mass affect potential energy if it is doubled?

The effect of doubling mass on potential energy is similar to doubling the height. By doubling the mass, the potential energy is also doubled, which becomes the reason to begin the work.

For example, a person is working out in the gym by lifting a barbell. The person has the maximum potential to lift the barbell; hence the work is done on the barbell by the person.

weightlifter g54f52c2e7 640
Image credits: Image by mohamed Hassan from Pixabay 

Suppose the mass is doubled by attaching some more weights to the barbell, then potential energy is also doubled because now the man has to exert more force to do the work on the barbell. So it is clear that potential energy will also become doubled with the mass.

Frequently Asked Questions

Does mass affect potential energy of a spring?

No, in the case of spring, the mass has nothing to do with the potential energy.

According to the theory of elasticity, the potential energy of spring is due to the stretching or elongation of the spring. Other than that, the mass of the spring is very much less compared to other quantities involved in the process. So the mass does not affect the potential energy of the spring.

Does mass affect potential energy of a molecule required to break the chemical bond?

Potential energy is stored in all the chemical molecules or atoms, responsible for breaking the bond and causing the chemical reaction.

Let us consider an example of the water molecule, which has two hydrogens and oxygen covalently bonded. The hydrogen atom and the oxygen atom have a certain mass, contributing to their interaction to form the bond. It has stored potential energy, which may release in the form of heat by breaking the bond. Thus it is evident that mass has affected the chemical potential energy.

Give examples for each type of potential energy

The examples for potential energy are:

Does the mass remain the same even after the potential energy is converted into kinetic energy?

Yes, mass is constant whether the potential energy converts or not.

Suppose an object is at a stationary state, and after the application of force, it begins to move. The stationary object possesses potential energy, and the same object possesses kinetic energy if it is in motion. Only the energy is transformed when the object begins to move, but the mass does not change even though the form of energy changes.

What do you mean by zero-point potential energy?

The potential energy is a capacity of a stationary body that is ready to work by imposing some force on the body.

Generally, the body should possess a certain mass, and it has to place at a distance to begin the work. If the body is at the ground level, its height is zero, so potential energy becomes zero. Practically even the height is zero, and the body possesses a certain amount of stored potential energy. This is taken as a reference called zero-point potential energy.

Also Read:

How to Calculate Speed from Force and Mass: 11 Facts to know

by
quicklatex.com b3c8813c1b20a8b6b70416ea0b3a3db5 l3

How to Calculate Speed from Force and Mass

In this blog post, we will dive into the fascinating world of physics and learn how to calculate the speed of an object using force and mass. Understanding this concept is crucial for grasping the fundamental principles of motion and how objects behave in different scenarios. So, let’s get started!

Understanding the Basic Concepts

Before we delve into the calculations, let’s familiarize ourselves with a few key concepts:

1. Definition of Speed

Speed can be defined as the rate at which an object covers distance over a given time. It tells us how fast an object is moving and is typically measured in meters per second m/s or kilometers per hour km/h. Speed is a scalar quantity, meaning it only has magnitude and no direction.

2. Definition of Force

Force, on the other hand, is a vector quantity that describes the interaction between two objects. It can cause an object to accelerate, decelerate, or change direction. Force is measured in Newtons N and is represented by the symbol “F”.

3. Definition of Mass

mass refers to the amount of matter an object contains. It is a scalar quantity and is typically measured in kilograms kg. The mass of an object remains constant regardless of its location in the universe.

The Relationship Between Force, Mass, and Speed

To understand how force and mass contribute to an object’s speed, we need to explore Newton’s Second Law of Motion and the role of acceleration.

1. Newton’s Second Law of Motion

Newton’s Second Law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Mathematically, we can represent this relationship with the equation:

F = ma

Where:
– F represents the force acting on the object,
– m represents the mass of the object, and
– a represents the acceleration.

2. The Role of Acceleration

acceleration is the rate at which an object’s velocity changes over time. It is also a vector quantity and is typically measured in meters per second squared m/s². In the context of speed calculation, acceleration plays a crucial role as it determines how quickly an object’s velocity changes.

By rearranging the formula for Newton’s Second Law, we can solve for acceleration:

a = frac{F}{m}

Now that we have a grasp of the basic concepts, let’s move on to the steps involved in calculating speed from force and mass.

Steps to Calculate Speed from Force and Mass

Calculating the speed of an object requires a multi-step approach. We’ll break it down into two main components: calculating acceleration from force and mass, and then calculating speed from acceleration and time.

A. Calculating Acceleration from Force and Mass

To find the acceleration, we’ll use the formula derived from Newton’s Second Law:

a = frac{F}{m}

1. The Formula for Acceleration

Acceleration a can be determined by dividing the force F acting on an object by its mass m. The resulting value will represent the rate at which the object’s velocity changes. Remember, force is measured in Newtons N and mass in kilograms kg.

2. Worked Out Example

Let’s consider an example to illustrate the calculation of acceleration. Suppose we have an object with a mass of 5 kg and a force of 20 N acting upon it. Using the formula mentioned earlier, we can calculate the acceleration as follows:

a = frac{F}{m} = frac{20 , text{N}}{5 , text{kg}} = 4 , text{m/s²}

So, the acceleration of the object is 4 m/s².

B. Calculating Speed from Acceleration and Time

Once we have the acceleration, we can proceed to calculate the speed of the object. To do this, we’ll employ the formula for speed:

v = at

1. The Formula for Speed

Speed v can be obtained by multiplying the acceleration a by the time t for which the object is subjected to that acceleration. acceleration is measured in meters per second squared m/s², and time is measured in seconds s.

2. Worked Out Example

Let’s continue with our example and calculate the speed of the object. Suppose the object is subjected to the acceleration of 4 m/s² for a period of 6 seconds. Plugging in the values into the formula, we get:

v = at = 4 , text{m/s²} times 6 , text{s} = 24 , text{m/s}

Hence, the speed of the object is 24 m/s.

Additional Considerations in Calculating Speed from Force and Mass

While the steps mentioned earlier provide a basic understanding of speed calculation, there are a few additional factors we should take into account for a more comprehensive analysis.

A. Calculating Initial and Final Velocity

In some scenarios, you might need to calculate the initial or final velocity of an object instead of its average speed. The initial velocity v_i refers to the object’s velocity at the beginning of a given time period, while the final velocity v_f represents its velocity at the end of that time period.

To calculate the initial or final velocity, you’ll need to know either the object’s acceleration a, the time t for which the acceleration is applied, and its initial or final speed v_i or v_f. You can use the formulas below to calculate the unknown velocity:

For initial velocity v_i:

v_i = v_f - at

For final velocity v_f:

v_f = v_i + at

B. Calculating Speed with Force, Mass, and Distance

Sometimes, you may come across situations where you need to calculate the speed of an object using force, mass, and distance. In such cases, you can utilize the concept of work-energy principle for the calculation.

1. The Role of Distance in Speed Calculation

The distance traveled by an object plays a significant role in determining its speed. It helps us understand how far the object has moved under the influence of the applied force.

2. How to Calculate Speed with Distance

To calculate speed using force, mass, and distance, you need to consider the concept of work done. Work done is the product of force and displacement. It can be calculated using the formula:

W = Fd

where:
– W represents the work done,
– F represents the force applied, and
– d represents the distance traveled.

By using the work-energy principle, we can relate the work done to the kinetic energy of the object. The formula for kinetic energy KE is:

KE = frac{1}{2}mv^2

where:
– m represents the mass of the object, and
– v represents the speed of the object.

Now, we can equate the work done to the change in kinetic energy:

W = Delta KE

By substituting the formula for work done and kinetic energy, we get:

Fd = frac{1}{2}mv^2

Simplifying the equation, we find:

v = sqrt{frac{2Fd}{m}}

Here, we can calculate the speed v by knowing the force F, distance d, and mass m of the object.

How does net force relate to calculating speed from force and mass?

The “Comparison between Net Force and Force” explains the distinction between net force and force. Net force is the vector sum of all the individual forces acting on an object, while force refers to a single push or pull exerted on an object. When calculating speed from force and mass, the concept of net force becomes crucial. By utilizing Newton’s second law (F = ma), we can determine net force by multiplying mass and acceleration. This net force can then be used to calculate speed using the equation v = u + at, where v represents final velocity, u denotes initial velocity, a indicates acceleration, and t represents time.

Common Mistakes and Misconceptions in Calculating Speed from Force and Mass

While calculating speed from force and mass, it’s important to be aware of common misconceptions and errors that can arise. Let’s address a couple of them:

A. Misconception about the Interchangeability of Speed and Velocity

speed and velocity are often used interchangeably in everyday language, but in physics, they have distinct meanings. While speed only considers the magnitude of an object’s motion, velocity takes into account both magnitude and direction. When calculating speed, make sure to consider its scalar nature and that it does not account for direction.

B. Common Errors in Using the Formulas

When working with formulas, it’s easy to make mistakes. Some common errors include using incorrect units, misplacing decimal points, or misinterpreting the given values. To avoid these errors, double-check your calculations, pay attention to unit conversions, and carefully analyze the information provided.

And there you have it! We have covered the steps involved in calculating speed from force and mass, as well as additional considerations and common mistakes. With these concepts in mind, you can now confidently apply the formulas and equations to solve various speed-related problems. Physics and mathematics are fascinating subjects, and understanding the principles behind motion can open up a whole new world of knowledge. Keep practicing, and soon you’ll be a pro at calculating speed from force and mass!

Also Read:

How To Calculate Mass From Weight: Several Approaches and Problem Examples

by
mass from weight 0
mass from weight 3

Calculating mass from weight is a fundamental concept in physics and engineering. Weight is the force exerted by an object due to gravity, while mass is the amount of matter present in an object. In this blog post, we will explore the relationship between weight and mass, and learn how to calculate mass from weight using various formulas and examples.

How to Calculate Mass from Weight

The Formula to Calculate Mass from Weight

To calculate mass from weight, we can use the equation:

\text{mass} = \frac{\text{weight}}{\text{acceleration due to gravity}}

The acceleration due to gravity on Earth is approximately 9.8 m/s^2. However, this value can vary depending on the location and altitude. Therefore, if you’re performing calculations in a different environment, make sure to use the appropriate acceleration due to gravity value.

Step-by-step Guide on How to Calculate Mass from Weight

To calculate mass from weight, follow these steps:

  1. Determine the weight of the object in Newtons.
  2. Identify the acceleration due to gravity at the location.
  3. Divide the weight by the acceleration due to gravity to find the mass.

Let’s go through an example to make the process clearer.

Worked out Examples on Calculating Mass from Weight

Example 1:
An object has a weight of 500 N. Calculate its mass.

Solution:
Using the formula, we have:
\text{mass} = \frac{\text{weight}}{\text{acceleration due to gravity}}

Substituting the given values, we get:
\text{mass} = \frac{500 \, \text{N}}{9.8 \, \text{m/s}^2} \approx 51.02 \, \text{kg}

Therefore, the mass of the object is approximately 51.02 kg.

Example 2:
A person weighs 750 N on the surface of Mars. Calculate their mass on Mars.

Solution:
First, we need to determine the acceleration due to gravity on Mars. Let’s assume it is 3.7 m/s^2.

Using the formula, we have:
\text{mass} = \frac{\text{weight}}{\text{acceleration due to gravity}}

Substituting the given values, we get:
\text{mass} = \frac{750 \, \text{N}}{3.7 \, \text{m/s}^2} \approx 202.7 \, \text{kg}

Therefore, the mass of the person on Mars is approximately 202.7 kg.

Advanced Concepts in Calculating Mass from Weight

how to calculate mass from weight
Image by Rickjpelleg – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY 2.5.

How to Calculate Mass from Weight and Volume

mass from weight 1

In some cases, you may need to calculate mass from weight and volume. To do this, you need to know the density of the material. The formula for calculating mass from weight and volume is:

\text{mass} = \text{weight} \times \text{density}

How to Calculate Mass from Weight and Gravity

mass from weight 2

When dealing with objects in different gravitational fields, the formula to calculate mass from weight and gravity is:

\text{mass} = \frac{\text{weight}}{\text{acceleration due to gravity}}

How to Calculate Mass from Molecular Weight

how to calculate mass from weight
Image by Incnis Mrsi – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

In chemistry, you can calculate the mass of a substance using its molecular weight. The formula to calculate mass from molecular weight is:

\text{mass} = \text{molecular weight} \times \text{number of moles}

How to Calculate Mass from Weight and Density

To calculate mass from weight and density, you can use the formula:

\text{mass} = \frac{\text{weight}}{\text{density}}

Practical Applications of Calculating Mass from Weight

Calculating Mass and Weight on Different Planets

The ability to calculate mass from weight is crucial when studying celestial bodies. By applying the concept of calculating mass from weight, scientists can determine the mass of objects on different planets or moons, providing insights into their composition and gravitational forces.

Converting Mass to Weight and Vice Versa

Knowing how to convert mass to weight and vice versa is useful in various fields. For example, in engineering, understanding the relationship between mass and weight is essential for designing structures and determining the loads they can withstand.

Calculating Mass from Weight in Different Units (Kg, Newtons)

Calculating mass from weight can be done using different units, such as kilograms (kg) or Newtons (N). It’s important to understand the correct units and conversions to ensure accurate calculations.

How can we calculate mass from weight and force? What insights can we gain by considering the concept of ‘Calculating mass from force and more’?

Calculating mass from force and more allows us to understand how weight and force can be used to determine the mass of an object. By exploring this concept, we can gain insights into the relationship between weight, force, and mass. This understanding is crucial in various fields, such as physics and engineering. By utilizing the methods discussed in the article, we can accurately calculate the mass of an object based on its weight and the force applied to it. This knowledge opens up possibilities for solving complex problems and making informed decisions.

Numerical Problems on how to calculate mass from weight

Problem 1:

A box weighs 25 N on Earth. What is the mass of the box?

Solution:
Given:
Weight of the box, W = 25 N

We know that weight is given by the formula:
W = m \cdot g

where:
W = weight of the object (in Newtons)
m = mass of the object (in kilograms)
g = acceleration due to gravity (approximately 9.8 m/s² on Earth)

To calculate the mass, we rearrange the formula as:
m = \frac{W}{g}

Substituting the given values into the formula, we get:
m = \frac{25 \, \text{N}}{9.8 \, \text{m/s²}}

Hence, the mass of the box is approximately 2.55 kg.

Problem 2:

A person weighs 650 N on Earth. What is their mass?

Solution:
Given:
Weight of the person, W = 650 N

Using the same formula as before, we have:
W = m \cdot g

Rearranging the formula to solve for mass:
m = \frac{W}{g}

Substituting the given values:
m = \frac{650 \, \text{N}}{9.8 \, \text{m/s²}}

Thus, the mass of the person is approximately 66.33 kg.

Problem 3:

An object has a weight of 1500 N on Earth. Determine its mass.

Solution:
Given:
Weight of the object, W = 1500 N

Applying the formula:
W = m \cdot g

Rearranging to find the mass:
m = \frac{W}{g}

Substituting the given values:
m = \frac{1500 \, \text{N}}{9.8 \, \text{m/s²}}

Therefore, the mass of the object is approximately 153.06 kg.

Also Read:

How To Calculate Mass From Force: Several Approaches and Problem Examples

by
mass from force 0

How to Calculate Mass from Force

In physics, understanding the relationship between mass and force is essential. By knowing how to calculate mass from force, we can analyze the behavior of objects and predict their motion accurately. In this blog post, we will explore various scenarios and formulas that will enable us to calculate mass using different factors such as force, acceleration, gravity, and distance.

Understanding the Basic Concepts

Before we dive into the calculations, let’s define the basic concepts of mass and force.

  1. Definition of Mass:
    Mass is a fundamental property of matter that measures the amount of substance in an object. It determines an object’s resistance to changes in its motion or acceleration. Mass is typically measured in kilograms (kg).

  2. Definition of Force:
    Force, on the other hand, is an external influence that can change an object’s motion. It can cause an object to accelerate, decelerate, or change direction. Force is measured in Newtons (N).

The Relationship Between Mass, Force, and Acceleration

mass from force 2

To understand how mass and force are related, we need to explore Newton’s Second Law of Motion and the formula F=ma.

  1. Newton’s Second Law of Motion:
    Newton’s Second Law states that the acceleration of an object is directly proportional to the net force applied to it and inversely proportional to its mass. Mathematically, it can be expressed as:

F = ma

Where:
– F represents the net force applied to the object (in Newtons).
– m represents the mass of the object (in kilograms).
– a represents the resulting acceleration of the object (in meters per second squared).

  1. The Formula F=ma:
    This formula allows us to calculate the force acting on an object when the mass and acceleration are known. It can also be rearranged to calculate the mass when the force and acceleration are given. The formula is as follows:

m = frac{F}{a}

By rearranging the formula, we can calculate the mass of an object by dividing the force acting on it by its acceleration.

Now that we have a clear understanding of the basic concepts and the formula involved, let’s move on to calculating mass from force in different scenarios.

How to Calculate Mass from Force and Acceleration

how to calculate mass from force
Image by Guy vandegrift – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

Step-by-Step Guide

mass from force 3

To calculate the mass of an object given the force and acceleration, follow these steps:

  1. Identifying the Given Variables:
    Determine the force acting on the object (F) and the resulting acceleration (a). Make sure the units are consistent (Newton for force and meters per second squared for acceleration).

  2. Applying the Formula:
    Plug in the values of force (F) and acceleration (a) into the formula m = frac{F}{a} and perform the calculation. The result will be the mass of the object.

Worked Out Examples

Let’s work through a couple of examples to solidify our understanding.

Example 1: Calculating Mass with Known Force and Acceleration

Suppose we have an object being pushed with a force of 10 N and experiencing an acceleration of 5 m/s². What is the mass of the object?

By using the formula m = frac{F}{a}, we can calculate the mass:
m = frac{10 , text{N}}{5 , text{m/s²}}

Simplifying the equation, we find that the mass of the object is 2 kg.

Example 2: Calculating Mass with Resultant Force and Acceleration

Now, let’s consider a situation where an object is subjected to a resultant force of 40 N, causing it to accelerate at a rate of 8 m/s². What is the mass of the object?

Using the formula m = frac{F}{a}, we can determine the mass:
m = frac{40 , text{N}}{8 , text{m/s²}}

After simplifying the equation, we find that the mass of the object is 5 kg.

By following these step-by-step instructions and using the formula m = frac{F}{a}, we can easily calculate the mass of an object when the force and acceleration are known.

In the next section, we will explore how to calculate mass from force and gravity.

How to Calculate Mass from Force and Gravity

how to calculate mass from force
Image by Guy vandegrift – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

Understanding the Concept of Gravity

Gravity is a fundamental force that attracts objects toward each other. It plays a crucial role in calculating mass, as it can influence the weight of an object.

  1. Definition of Gravity:
    Gravity is the force of attraction between two objects with mass. On Earth, gravity pulls objects towards the center of the planet.

  2. The Role of Gravity in Calculating Mass:
    When we calculate mass from force and gravity, we are essentially determining the weight of an object, as weight is the force exerted on an object due to gravity. Weight is given by the formula:

W = mg

Where:
– W represents the weight of the object (in Newtons).
– m represents the mass of the object (in kilograms).
– g represents the acceleration due to gravity, which is approximately 9.8 m/s² on Earth.

Step-by-Step Guide

To calculate the mass of an object given the force and gravity, follow these steps:

  1. Identifying the Given Variables:
    Determine the force acting on the object (F) and the acceleration due to gravity (g). Ensure the units are consistent (Newton for force and meters per second squared for acceleration).

  2. Applying the Formula:
    Plug in the values of force (F) and the acceleration due to gravity (g) into the formula W = mg and solve for the mass (m).

Now, let’s dive into some worked-out examples to grasp the concept better.

Worked Out Examples

Example 1: Calculating Mass with Known Force and Gravity

Suppose we have an object experiencing a force of 50 N due to gravity. What is the mass of the object?

Using the formula W = mg, we can calculate the weight of the object. Since weight is equal to force, we have:
50 , text{N} = mg

Since we know that the acceleration due to gravity is approximately 9.8 m/s², we can rearrange the formula to solve for mass:
m = frac{50 , text{N}}{9.8 , text{m/s²}}

Evaluating the equation, we find that the mass of the object is approximately 5.1 kg.

Example 2: Calculating Mass on Different Planets

Let’s explore how to calculate the mass of an object on a different planet. Suppose an object has a weight of 60 N on a planet where the acceleration due to gravity is 20 m/s². What is the mass of the object on this planet?

Using the formula W = mg, we can rearrange the equation to solve for mass:
m = frac{W}{g}

Substituting the given values, we have:
m = frac{60 , text{N}}{20 , text{m/s²}}

Computing the equation, we find that the mass of the object on this planet is 3 kg.

By following these step-by-step instructions and applying the formula W = mg, we can easily calculate the mass of an object when the force and gravity are known.

In the next section, we will delve into calculating mass from force and distance.

How to Calculate Mass from Force and Distance

Understanding the Concept of Distance in Physics

In physics, distance refers to the amount of space between two points, typically measured in meters (m). Distance is a crucial factor when calculating mass, as it can affect the force exerted on an object.

  1. Definition of Distance:
    Distance is the measurement of the space between two points in a physical system.

  2. The Role of Distance in Calculating Mass:
    Distance plays a key role in determining the work done on an object, which is equal to the force exerted on the object multiplied by the distance it moves. The formula for work in this scenario is given by:

W = Fd

Where:
– W represents the work done on the object (in Joules).
– F represents the force acting on the object (in Newtons).
– d represents the distance the object moves (in meters).

Step-by-Step Guide

To calculate the mass of an object given the force and distance, follow these steps:

  1. Identifying the Given Variables:
    Determine the force acting on the object (F) and the distance it moves (d). Ensure the units are consistent (Newton for force and meters for distance).

  2. Applying the Formula:
    Plug in the values of force (F) and distance (d) into the formula W = Fd. Calculate the work done on the object.

Now, let’s explore a couple of examples to solidify our understanding.

Worked Out Examples

Example 1: Calculating Mass with Known Force and Distance

Let’s say we have an object subjected to a constant force of 20 N, causing it to move a distance of 5 meters. What is the mass of the object?

Using the formula W = Fd, we can calculate the work done on the object. Since work is equal to the force multiplied by the distance, we have:
W = 20 , text{N} times 5 , text{m}

Simplifying the equation, we find that the work done on the object is 100 J.

Since we know that work is equal to the force multiplied by the distance, we can rearrange the formula to solve for mass:
m = frac{W}{d}

Substituting the known values, we have:
m = frac{100 , text{J}}{5 , text{m}}

Evaluating the equation, we find that the mass of the object is 20 kg.

Example 2: Calculating Mass in Different Scenarios

Now, let’s consider a scenario where an object is acted upon by a force of 30 N and moves a distance of 10 meters. What is the mass of the object?

Using the formula W = Fd, we can first calculate the work done on the object:
W = 30 , text{N} times 10 , text{m}

Simplifying the equation, we find that the work done on the object is 300 J.

By rearranging the formula m = frac{W}{d}, we can solve for the mass:
m = frac{300 , text{J}}{10 , text{m}}

After evaluating the equation, we find that the mass of the object is 30 kg.

By following these step-by-step instructions and applying the formula W = Fd, we can calculate the mass of an object when the force and distance are known.

In the next section, we will explore how to calculate mass without force.

How to Calculate Mass without Force

Understanding the Concept of Mass without Force

In certain situations, we may need to calculate the mass of an object without having direct information about the force acting on it. Fortunately, there are other variables that we can utilize to determine the mass.

  1. The Role of Other Variables in Calculating Mass:
    When force is unknown, we can still use other variables such as momentum, kinetic energy, or gravitational potential energy to calculate the mass of an object. These variables are dependent on mass and other known quantities.

To calculate mass without force, we need to consider the specific scenario and select an appropriate formula. Let’s explore a general step-by-step guide to calculating mass without force.

Step-by-Step Guide

To calculate the mass of an object without knowing the force, follow these steps:

  1. Identifying the Given Variables:
    Determine the known variables in the given scenario. These can include factors such as momentum, kinetic energy, or gravitational potential energy.

  2. Applying the Formula:
    Select the appropriate formula based on the known variables and rearrange it to solve for mass. Depending on the scenario, you may need to refer to specific formulas related to momentum, kinetic energy, or potential energy.

Now, let’s work through a couple of examples to illustrate how to calculate mass without force.

Worked Out Examples

Example 1: Calculating Mass without Known Force

Suppose we have an object with a momentum of 25 kg·m/s. The force acting on the object is unknown. What is the mass of the object?

To calculate the mass without knowing the force, we can use the formula for momentum:
p = mv

Rearranging the formula, we can solve for mass:
m = frac{p}{v}

Substituting the given values, we have:
m = frac{25 , text{kg·m/s}}{v}

Since the velocity (v) is unknown, we cannot determine the mass in this scenario without additional information.

Example 2: Calculating Mass in Different Scenarios

Let’s consider a scenario where an object has a kinetic energy of 100 J but the force acting on it is unknown. What is the mass of the object?

The formula for kinetic energy is:
KE = frac{1}{2}mv^2

Rearranging the formula, we can solve for mass:
m = frac{2KE}{v^2}

Substituting the given values, we have:
m = frac{2(100 , text{J})}{v^2}

Without the value of velocity (v), we cannot determine the mass in this scenario.

By following this step-by-step guide and selecting the appropriate formula for the given variables, we can calculate the mass of an object even without knowing the force.

In this blog post, we explored the various methods of calculating mass from force. We started by understanding the basic concepts of mass and force, followed by exploring the relationship between mass, force, and acceleration using Newton’s Second Law of Motion. We then delved into calculating mass from force and acceleration, force and gravity, force and distance, and even without knowing the force. Throughout the post, we provided step-by-step instructions and worked-out examples to ensure a thorough understanding of the calculations involved.

Understanding how to calculate mass from force is crucial in physics and allows us to analyze and predict the behavior of objects. By mastering these calculations, you will be well-equipped to tackle a wide range of physics problems. Remember to practice these calculations regularly to reinforce your understanding and build confidence in your skills.

So, keep practicing, stay curious, and embrace the wonders of physics!

How can the concept of calculating mass from force be related to the process of calculating mass from weight?

Calculating mass from weight: step-by-step is an essential process in understanding the relationship between force and weight. To bridge the gap between these concepts, it is necessary to explore how force and weight are interconnected. The article Calculating mass from weight: step-by-step. provides a comprehensive explanation of the process, highlighting the significance of weight in determining mass. By understanding the relationship between force, weight, and mass, it becomes clear how these two topics intersect and contribute to a deeper understanding of physics.

Numerical Problems on how to calculate mass from force

mass from force 1

Problem 1:

A force of 20 N is applied to an object, causing it to accelerate at a rate of 5 m/s². Calculate the mass of the object.

Solution:

We can use Newton’s second law of motion to solve this problem. Newton’s second law states that the force acting on an object is equal to the mass of the object multiplied by its acceleration.

So, we have:

F = ma

where:
– F is the force (given as 20 N),
– m is the mass (to be determined), and
– a is the acceleration (given as 5 m/s²).

Now, let’s solve for the mass:

m = frac{F}{a} = frac{20, text{N}}{5, text{m/s²}} = 4, text{kg}

Therefore, the mass of the object is 4 kg.

Problem 2:

An object of mass 2 kg accelerates at a rate of 10 m/s². Calculate the force acting on the object.

Solution:

Again, we’ll use Newton’s second law of motion to solve this problem. Rearranging the equation, we have:

F = ma

where:
– F is the force (to be determined),
– m is the mass (given as 2 kg), and
– a is the acceleration (given as 10 m/s²).

Substituting the given values, we get:

F = 2, text{kg} cdot 10, text{m/s²} = 20, text{N}

Therefore, the force acting on the object is 20 N.

Problem 3:

An object with a mass of 5 kg experiences a force of 25 N. Calculate the acceleration of the object.

Solution:

Once again, we’ll use Newton’s second law of motion. Rearranging the equation, we have:

F = ma

where:
– F is the force (given as 25 N),
– m is the mass (given as 5 kg), and
– a is the acceleration (to be determined).

Substituting the given values, we have:

25, text{N} = 5, text{kg} cdot a

To solve for a , we can rearrange the equation:

a = frac{F}{m} = frac{25, text{N}}{5, text{kg}} = 5, text{m/s²}

Therefore, the acceleration of the object is 5 m/s².

Also Read:

How to Calculate Mass from Gravitational Force: Several Approaches and Problem Examples

by
mass from gravitational force 0

How to Calculate Mass from Gravitational Force

In this blog post, we will explore the concept of calculating mass from gravitational force. We will start by understanding the key terms related to this topic, such as gravitational force, mass in physics, and the concept of gravity. Then, we will dive into the gravity equation and its importance in calculations.

Definition of Key Terms

mass from gravitational force 2
  1. Understanding Gravitational Force:
    Gravitational force is the attractive force between two objects with mass. It is responsible for keeping planets in orbit around the sun and objects grounded on Earth. The force of gravity can be calculated using the equation:

F = frac{{G cdot m_1 cdot m_2}}{{r^2}}

where F is the gravitational force, G is the gravitational constant, m_1 and m_2 are the masses of the two objects, and r is the distance between them.

  1. Defining Mass in Physics:
    In physics, mass refers to the amount of matter an object contains. It is a fundamental property of an object and is measured in kilograms (kg). Mass can be calculated using the formula:

m = frac{F}{g}

where m is the mass, F is the gravitational force acting on the object, and g is the acceleration due to gravity.

  1. The Concept of Gravity:
    Gravity is the force that attracts two objects with mass towards each other. It is what gives weight to objects and keeps them grounded on the surface of the Earth. The force of gravity is directly proportional to the masses of the objects and inversely proportional to the square of the distance between them.

The Gravity Equation

  1. Breaking Down the Gravity Formula:
    The gravity formula, also known as Newton’s law of gravitation, is given by:

F = frac{{G cdot m_1 cdot m_2}}{{r^2}}

This equation allows us to calculate the gravitational force between two objects. F represents the gravitational force, G is the gravitational constant (6.67430 times 10^{-11} , text{Nm}^2/text{kg}^2), m_1 and m_2 are the masses of the two objects, and r is the distance between them.

  1. Importance of the Gravity Equation in Calculations:
    The gravity equation is crucial in various fields of science and engineering. It helps us understand the behavior of celestial bodies, calculate the gravitational force between objects, determine the motion of satellites, and even explore the universe. Without this equation, our understanding of the cosmos and the physical world would be severely limited.

The Relationship Between Gravitational Force and Mass

mass from gravitational force 1

A. Does Gravitational Force Depend on Mass?

  1. Exploring the Dependency of Gravitational Force on Mass:
    Yes, the gravitational force between two objects depends on their masses. According to Newton’s law of gravitation, the force of gravity is directly proportional to the product of the masses of the two objects (m_1 and m_2). As the masses increase, so does the gravitational force between them.

  2. How Mass Affects Gravitational Force:
    Increasing the mass of one or both objects involved in the gravitational interaction will result in a stronger gravitational force. Conversely, decreasing the mass will lead to a weaker force of gravity. This relationship highlights the importance of mass in determining the strength of gravitational interactions.

B. How Gravitational Force is Related to Mass and Distance

  1. The Role of Distance in Gravitational Force:
    The distance between two objects also plays a crucial role in determining the gravitational force between them. According to the inverse square law, the force of gravity decreases as the distance between the objects increases. In other words, the force is inversely proportional to the square of the distance (r).

  2. The Interplay Between Mass, Distance, and Gravitational Force:
    The interplay between mass and distance is evident in the gravity equation (F = frac{{G cdot m_1 cdot m_2}}{{r^2}}). As the masses of the objects increase, the force of gravity becomes stronger. Similarly, as the distance between the objects decreases, the force of gravity also increases. These relationships highlight how both mass and distance affect the gravitational force between two objects.

Calculating Mass Given Gravitational Force

how to calculate mass from gravitational force
Image by Karl-Ludwig Poggemann – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY 2.0.

A. Steps to Calculate Mass Using Gravitational Force

  1. Detailed Process of Calculating Mass:
    To calculate mass from gravitational force, we can rearrange the mass formula (m = frac{F}{g}) to solve for mass (m). The steps involved are as follows:
  2. Identify the gravitational force acting on the object (F).
  3. Determine the acceleration due to gravity (g).

  4. Substitute the values into the formula m = frac{F}{g} to calculate the mass.

  5. Worked Out Examples for Better Understanding:
    Let’s consider an example to demonstrate the calculation of mass from gravitational force. Suppose an object experiences a gravitational force of 50 N and the acceleration due to gravity is 9.8 m/s^2. Using the formula m = frac{F}{g}, we can calculate the mass as follows:

m = frac{50 , text{N}}{9.8 , text{m/s}^2} = 5.10 , text{kg}

Therefore, the mass of the object is 5.10 kg.

B. How to Use the Gravity Formula to Find Mass

  1. Practical Application of the Gravity Formula:
    The gravity formula (F = frac{{G cdot m_1 cdot m_2}}{{r^2}}) can also be used to find the mass of an object. By rearranging the equation, we can solve for mass (m_2) when the gravitational force (F), the mass of the first object (m_1), and the distance between the objects (r) are known.

  2. Examples of Using the Gravity Formula to Calculate Mass:
    Let’s consider an example where the gravitational force between two objects is 100 N, the distance between them is 2 meters, and the mass of one object is 5 kg. We can use the gravity formula to find the mass of the second object (m_2) as follows:

m_2 = frac{{F cdot r^2}}{{G cdot m_1}} = frac{{100 , text{N} cdot (2 , text{m})^2}}{{6.67430 times 10^{-11} , text{Nm}^2/text{kg}^2 cdot 5 , text{kg}}} approx 5.99 times 10^{11} , text{kg}

Therefore, the mass of the second object is approximately 5.99 times 10^{11} kg.

Calculating Gravitational Force Without Mass

mass from gravitational force 3

A. Understanding the Process of Calculating Gravitational Force

  1. Steps to Calculate Gravitational Force Without Mass:
    The gravitational force between two objects can be calculated even when the masses of the objects are unknown. If we know the acceleration due to gravity (g) and the mass of one of the objects (m_1), we can find the gravitational force (F). The steps involved are as follows:
  2. Identify the acceleration due to gravity (g).
  3. Determine the mass of one of the objects involved (m_1).

  4. Substitute the values into the formula F = G cdot frac{{m_1 cdot m_2}}{{r^2}} and solve for F.

  5. Examples to Illustrate the Calculation Process:
    Let’s consider an example where the acceleration due to gravity is 9.8 , text{m/s}^2, the mass of one object is 2 , text{kg}, and the distance between the objects is 3 , text{m}. Using the formula F = G cdot frac{{m_1 cdot m_2}}{{r^2}}, we can calculate the gravitational force as follows:

F = 6.67430 times 10^{-11} , text{Nm}^2/text{kg}^2 cdot frac{{2 , text{kg} cdot m_2}}{{(3 , text{m})^2}}

Since the mass of the second object (m_2) is unknown, we cannot calculate the exact value of the gravitational force. However, we can see that the force will be directly proportional to m_2 and inversely proportional to the square of the distance.

B. How to Calculate Gravitational Force Weight

  1. The Relationship Between Gravitational Force and Weight:
    Weight is the force experienced by an object due to gravity. The weight of an object can be calculated using the formula:

W = m cdot g

where W is the weight, m is the mass of the object, and g is the acceleration due to gravity.

  1. Steps and Examples to Calculate Weight from Gravitational Force:
    To calculate weight from gravitational force, we can rearrange the weight formula (W = m cdot g) to solve for the mass (m). The steps involved are as follows:
  2. Identify the gravitational force acting on the object (F).
  3. Determine the acceleration due to gravity (g).
  4. Substitute the values into the formula W = m cdot g to calculate the weight.

Let’s consider an example where the gravitational force acting on an object is 100 , text{N} and the acceleration due to gravity is 9.8 , text{m/s}^2. Using the formula W = m cdot g, we can calculate the weight as follows:

W = frac{F}{g} = frac{100 , text{N}}{9.8 , text{m/s}^2} approx 10.20 , text{kg}

Therefore, the weight of the object is approximately 10.20 , text{kg}.

Recap of How to Calculate Mass from Gravitational Force

In this blog post, we have discussed how to calculate mass from gravitational force. We started by understanding the key terms, such as gravitational force, mass in physics, and the concept of gravity. Then, we explored the gravity equation and its importance in calculations.

We also delved into the relationship between gravitational force and mass, highlighting how mass affects gravitational force and the interplay between mass, distance, and gravitational force. Additionally, we learned how to calculate mass given gravitational force and how to calculate gravitational force without mass.

Understanding these calculations is crucial in the fields of physics and engineering. They allow us to analyze the behavior of celestial bodies, calculate the motion of satellites, and comprehend the fundamental laws of nature. I encourage you to further explore and learn about these fascinating concepts to deepen your understanding of the universe and our place within it.

How can mass be calculated using both gravitational force and force and distance?

Calculating mass involves various methods depending on the available information. One method is calculating mass using gravitational force. This approach utilizes Newton’s law of universal gravitation to determine the mass of an object based on the gravitational force acting on it. Another method is calculating mass using force and distance. This technique involves applying Newton’s second law of motion and considering the force applied to an object and the distance it moves. By integrating these two methods, we can determine mass using both gravitational force and force and distance. To learn more about calculating mass using force and distance, visit Calculating mass using force and distance.

Numerical Problems on how to calculate mass from gravitational force

Problem 1:

A satellite is in orbit around a planet with a gravitational force of 2.5 N. If the distance between the satellite and the planet is 500 km, calculate the mass of the planet.

Solution:

Given:
Gravitational force (F) = 2.5 N
Distance (r) = 500 km = 500,000 m

Using the formula for gravitational force:

F = frac{{G cdot m_1 cdot m_2}}{{r^2}}

where:
G is the gravitational constant,
m_1 and m_2 are the masses of the two objects, and
r is the distance between the objects.

To calculate the mass of the planet (m_2), rearrange the formula:

m_2 = frac{{F cdot r^2}}{{G cdot m_1}}

Substituting the given values:

m_2 = frac{{2.5 cdot (500,000)^2}}{{G cdot m_1}}

The values for G and m_1 are constants, so let’s assume G = 6.67 × 10^-11 N m^2/kg^2 and m_1 = 1 kg for simplicity.

m_2 = frac{{2.5 cdot (500,000)^2}}{{(6.67 × 10^{-11}) cdot 1}}

m_2 = frac{{2.5 cdot 250,000,000,000}}{{6.67 × 10^{-11}}}

Simplifying the expression, we get:

m_2 = 9.375 times 10^{12} , text{kg}

Therefore, the mass of the planet is approximately 9.375 × 10^12 kg.

Problem 2:

The gravitational force between two objects is 6.7 × 10^-8 N. If the masses of the objects are 2 kg and 4 kg respectively, calculate the distance between them.

Solution:

Given:
Gravitational force (F) = 6.7 × 10^-8 N
Mass of object 1 (m_1) = 2 kg
Mass of object 2 (m_2) = 4 kg

Using the formula for gravitational force:

F = frac{{G cdot m_1 cdot m_2}}{{r^2}}

Rearranging the formula to solve for the distance (r):

r = sqrt{frac{{G cdot m_1 cdot m_2}}{{F}}}

Substituting the given values:

r = sqrt{frac{{(6.67 × 10^{-11}) cdot 2 cdot 4}}{{6.7 × 10^{-8}}}}

Simplifying the expression, we get:

r = sqrt{frac{{53.36 × 10^{-11}}}{{6.7 × 10^{-8}}}}

r = sqrt{frac{{53.36}}{{6.7}} times 10^{-11} times 10^{8}}

r = sqrt{{7.97 times 10^{-3}}} times 10^{8}

r = 2.82 times 10^{4} , text{m}

Therefore, the distance between the two objects is approximately 2.82 × 10^4 meters.

Problem 3:

The gravitational force between two objects is 9.8 N. If the distance between them is 10 meters, calculate the combined mass of the objects.

Solution:

Given:
Gravitational force (F) = 9.8 N
Distance (r) = 10 m

Using the formula for gravitational force:

F = frac{{G cdot m_1 cdot m_2}}{{r^2}}

Rearranging the formula to solve for the combined mass (m_1 + m_2):

m_1 + m_2 = frac{{F cdot r^2}}{{G}}

Substituting the given values and assuming G = 6.67 × 10^-11 N m^2/kg^2:

m_1 + m_2 = frac{{9.8 cdot 10^2}}{{6.67 × 10^{-11}}}

Simplifying the expression, we get:

m_1 + m_2 = frac{{98}}{{6.67}} times 10^9

m_1 + m_2 = 14.79 times 10^9

Therefore, the combined mass of the objects is approximately 14.79 × 10^9 kg.

Also Read:

How To Find Normal Force With Mass: Several Approaches And Problem Examples

by
normal force with mass 0
normal force with mass 3

When it comes to understanding the concept of normal force with mass, we need to delve into the fascinating world of physics. Normal force is the force exerted by a surface to support the weight of an object resting on it. In this blog post, we will explore how to calculate normal force with mass, including the role of gravity, the equation for finding normal force, and various factors that affect it. So, let’s dive in and unravel the mysteries of normal force with mass!

Calculating Normal Force with Mass

The Role of Gravity in Determining Normal Force

Before we delve into the calculations, it’s important to understand the role of gravity in determining the normal force. Gravity is the force that pulls objects towards the center of the Earth. When an object is at rest on a surface, the force of gravity acts vertically downwards. The normal force, on the other hand, acts perpendicular to the surface and counteracts the force of gravity. It prevents the object from sinking into the surface or falling through it.

The Equation for Finding Normal Force with Mass

To calculate the normal force with mass, we can use the equation:

\text{Normal Force (N)} = \text{Mass (kg)} \times \text{Gravity (m/s}^2)

The mass is measured in kilograms (kg), and the gravity is typically taken as 9.8 m/s^2 on the surface of the Earth. By multiplying the mass of an object by the acceleration due to gravity, we can determine the normal force acting on it.

Worked Out Examples on How to Find Normal Force with Mass

Let’s work through a couple of examples to solidify our understanding.

Example 1:

Suppose we have a block with a mass of 10 kg resting on a table. What is the normal force acting on the block?

We can use the equation we mentioned earlier:

\text{Normal Force (N)} = \text{Mass (kg)} \times \text{Gravity (m/s}^2)

Substituting the given values, we get:

\text{Normal Force (N)} = 10 \, \text{kg} \times 9.8 \, \text{m/s}^2 = 98 \, \text{N}

Therefore, the normal force acting on the block is 98 N.

Example 2:

Let’s consider a person with a mass of 60 kg standing on a bathroom scale. What is the reading on the scale?

Again, we can use the equation:

\text{Normal Force (N)} = \text{Mass (kg)} \times \text{Gravity (m/s}^2)

Plugging in the values, we have:

\text{Normal Force (N)} = 60 \, \text{kg} \times 9.8 \, \text{m/s}^2 = 588 \, \text{N}

Therefore, the reading on the bathroom scale would be 588 N.

Factors Affecting Normal Force

The Impact of Angle on Normal Force

The angle at which an object is placed on a surface can affect the normal force acting on it. When an object is on an inclined plane, the normal force is not equal to the object’s weight. Instead, it can be calculated using trigonometry. The normal force can be determined by multiplying the weight of the object by the cosine of the angle of inclination.

The Effect of Friction on Normal Force

Friction plays a crucial role in determining the normal force when there is relative motion or an impending motion between two surfaces. In such cases, the normal force can be reduced due to the opposing force of friction. The magnitude of the frictional force depends on the coefficient of friction, which is a measure of the friction between the two surfaces.

The Influence of Applied Force on Normal Force

When an external force is applied to an object, it can affect the normal force acting on it. If a force is applied in a direction perpendicular to the surface, it can alter the normal force. For example, if you push down on an object, the normal force will increase. Conversely, if you pull up on an object, the normal force will decrease.

Advanced Concepts in Normal Force

How to Determine Normal Force with Mass and Acceleration

In some cases, we may need to calculate the normal force when an object is accelerating. To do this, we need to consider the net force acting on the object. The net force is the vector sum of all the forces acting on the object. When an object is accelerating, the net force is given by the product of the mass and acceleration. The normal force can then be calculated by subtracting the force due to gravity from the net force.

How to Measure Normal Force with Mass and Coefficient of Friction

normal force with mass 1

In situations where there is friction between two surfaces, the normal force can be determined by considering the force of friction. The force of friction can be calculated by multiplying the coefficient of friction by the normal force. Rearranging this equation, we can solve for the normal force by dividing the force of friction by the coefficient of friction.

Worked Out Examples on Advanced Concepts

Let’s explore a couple of examples involving advanced concepts of normal force.

Example 3:

Suppose we have an object of mass 5 kg experiencing an acceleration of 2 m/s^2. What is the normal force acting on the object?

Using the equation for net force:

\text{Net Force} = \text{Mass} \times \text{Acceleration}

Substituting the given values, we have:

\text{Net Force} = 5 \, \text{kg} \times 2 \, \text{m/s}^2 = 10 \, \text{N}

Since the object is not accelerating vertically, the net force acting on it must be equal to the normal force. Therefore, the normal force is 10 N.

Example 4:

Consider a box with a coefficient of friction of 0.4. If the force of friction between the box and the surface is 20 N, what is the normal force acting on the box?

Using the equation for force of friction:

\text{Force of Friction} = \text{Coefficient of Friction} \times \text{Normal Force}

Rearranging the equation to solve for the normal force, we get:

\text{Normal Force} = \frac{\text{Force of Friction}}{\text{Coefficient of Friction}} = \frac{20 \, \text{N}}{0.4} = 50 \, \text{N}

Therefore, the normal force acting on the box is 50 N.

Understanding how to find normal force with mass is crucial when it comes to analyzing the forces at play in various situations. By considering the role of gravity, applying the equation for finding normal force, and being aware of the factors that affect it, we can accurately determine the normal force acting on an object. So, whether you’re studying physics or simply curious about the world around you, the concept of normal force with mass is an important piece of the puzzle that allows us to better understand the forces that shape our everyday experiences.

Can the normal force be at an angle? How does understanding normal force at an angle relate to finding normal force with mass?

The concept of normal force is commonly associated with finding the force exerted by a surface on an object. However, it is important to understand that the normal force can also exist at an angle. This understanding is crucial when exploring the relationship between finding normal force with mass and analyzing situations where the normal force is not purely vertical. To gain insights into the complexities of normal force at an angle, it is recommended to refer to the article on Understanding normal force at an angle. This article provides in-depth information about situations where the normal force deviates from being purely perpendicular to the surface, shedding light on how to accurately calculate and interpret such forces.

Numerical Problems on how to find normal force with mass

Problem 1:

A car of mass m is moving on a horizontal road with a constant velocity. Find the normal force exerted by the road on the car.

Solution:

The normal force \(N) exerted by the road on the car is equal in magnitude and opposite in direction to the gravitational force \(mg) acting on the car. Therefore, we can calculate the normal force using the equation:

N = mg

where:
m = mass of the car

Problem 2:

normal force with mass 2

A block of mass m is resting on a horizontal surface. Determine the normal force exerted by the surface on the block.

Solution:

When an object is at rest on a horizontal surface, the normal force \(N) exerted by the surface on the object is equal in magnitude and opposite in direction to the gravitational force \(mg) acting on the object. Thus, we can calculate the normal force using the equation:

N = mg

where:
m = mass of the block

Problem 3:

A person of mass m is standing on a weighing scale inside an elevator. Calculate the normal force exerted by the scale on the person when the elevator is:

a) Accelerating upwards with acceleration a
b) Accelerating downwards with acceleration a
c) Moving upwards with constant velocity
d) Moving downwards with constant velocity

Solution:

a) When the elevator is accelerating upwards, the normal force \(N) exerted by the scale on the person is given by:

N = mg + ma

where:
m = mass of the person
g = acceleration due to gravity
a = acceleration of the elevator

b) When the elevator is accelerating downwards, the normal force \(N) exerted by the scale on the person is given by:

N = mg - ma

where:
m = mass of the person
g = acceleration due to gravity
a = acceleration of the elevator

c) When the elevator is moving upwards with constant velocity, the normal force \(N) exerted by the scale on the person is equal in magnitude and opposite in direction to the gravitational force \(mg) acting on the person. Thus, we can calculate the normal force using the equation:

N = mg

where:
m = mass of the person

d) When the elevator is moving downwards with constant velocity, the normal force \(N) exerted by the scale on the person is equal in magnitude and opposite in direction to the gravitational force \(mg) acting on the person. Thus, we can calculate the normal force using the equation:

N = mg

where:
m = mass of the person

Also Read: