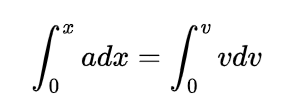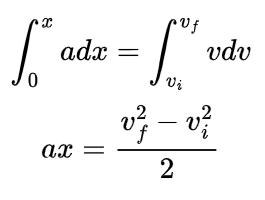Find - lambdageeks.com

How To Find Velocity With Height:Different Approaches,Problems,Examples

January 20, 2024January 8, 2022 by Keerthi Murthi

When an object is dropped from a certain height, the force of gravity largely influences the object to attain more velocity. So it is clear that height is an entity that influences motion.

A freely falling object initially attains zero velocity, and as it begins to move downward, it gains velocity. Suppose we know the only height of the falling object, how to find velocity with height, and also along with the height, how the other entities influence over velocity are explained in this post.

How to find velocity with Height?

Consider a book kept on a table at the height of h from the ground. When the book falls from the table, then how fast the book falls on the ground is given by velocity. Since the book is at the height of h, how to find the velocity with height?

v h 2 — Book falling from certain height to show how to find velocity with height

We know that velocity can be calculated from knowing the distance traveled by the body, and the time taken by it to reach that distance. Mathematically it can be written as,

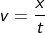
In the example given above, we are provided with the height h. The height of the body is associated with potential energy. So the basic equation is not valid.

Considering the potential energy possessed by the book before it falls, expression can be written as,

PE = mgh.

But the book is under motion; hence the potential energy is now turned into kinetic energy as

Thus, the potential energy and kinetic energy are equal by the conservation of energy. Hence the equation can be written as

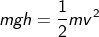
By rearranging the equation, we get velocity as

v² = 2gh

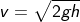
In the above equation, g is the acceleration due to gravity. Any object falling from a certain height is influenced by gravity and is constantly accelerating more due to gravity.

How to find velocity with acceleration and height?

We know how to find velocity with acceleration and distance from the previous article. But we have given with acceleration and height then how to find velocity with acceleration and height instead of distance?

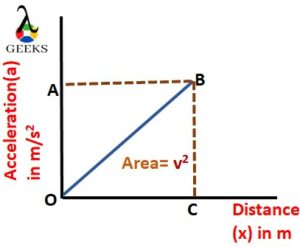
Acceleration and velocity are the proportional entities as the time derivative of velocity is acceleration. If we have acceleration means, on integrating the acceleration, we can have velocity. But in this case, we have acceleration and height. Let us discuss how to find velocity with height if acceleration is given.

Consider a ball is at a certain height above the ground. The ball is dropped from the height ‘h,’ and it begins to accelerate at ‘a’ is in the direction of acceleration due to gravity; this means that the ball is falling from the height h in the direction of gravitational pull.

Since both acceleration and acceleration due to gravity are in the same direction, the total acceleration of the body is equal to the sum of both accelerations of the body and acceleration due to gravity A = g+a. Now the ball’s velocity can be calculated using the equation of motion.

We know from the kinematic equation of motion, distance traveled by the body can be written in terms of the mathematical equation as,

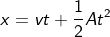
But, we have the height of the ball and the acceleration. The distance can be written in terms of height as,

The ball’s initial position when it begins to move and the final position of the ball gives the distance.

Therefore x = h – 0, i.e., x=h, we can say vertical distance as height. Now substituting the x = h, we have the equation as

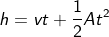
Rearranging the above equation, we have

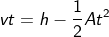
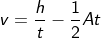
The equation obtained above gives the velocity of the ball given acceleration and height.

Let us set another example if a projectile moving towards the ground from the height h, and its acceleration is more than the acceleration due to gravity because the projectile is overcome from the air friction, then the equation of the velocity will be calculated as,

In the kinematics equations, the velocity is given by

v² = 2Ax

Where x is the distance. But here x = h, then

v² = 2Ah

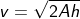
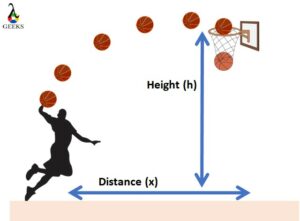
Consider another case; if you throw a ball in the air, after reaching the height h, the ball begins to accelerate downward due to gravity; the motion is called projectile motion; in this situation, how to find velocity with acceleration and height? The ball’s motion in the air is given in the below figure.

how to find velocity with acceleration and height — Diagram showing how find velocity with acceleration and height using projectile motion

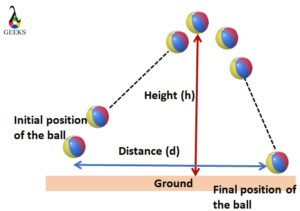
From the above figure, the object’s height is h, and distance is not the height, but we have height in terms of distance by using the equation of projectile motion. The relation between distance and height can be written as,

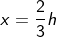
Substituting the value of distance in the equation of motion, we get

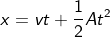
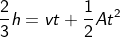
Rearranging the equation, we get velocity as

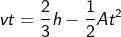
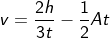
How to find initial velocity with acceleration and height?

The initial velocity can be derived from the acceleration and height, considering the equation of motion.

A body is accelerating means there must be a change in the velocity of the body with a given instance, which also tells that initially, the body has some velocity that keeps on changing with time. So to find the initial velocity, we need to know the final velocity of the body.

When we throw a ball in the air, it reaches a certain height h with a certain velocity and attains acceleration a. Initially; the ball moves with velocity vi. Finally, the velocity will be vf. The equation of initial velocity will be written using the equation of motion of the ball can be calculated as follow.

The velocity can be

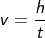
The final velocity of the ball is given as vf, hence from the average velocity.

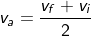
But at the height h, the ball acquires zero final velocity as it falls back to the ground due to gravity.

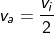
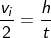
But we don’t know the time taken by the ball to reach the height h., so we can use the acceleration. Initially, the ball is accelerating against gravity; its acceleration will become negative.

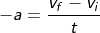
We know the final velocity is zero, then

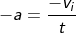
Therefore we get the time factor as

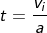
Substituting in the equation of average initial velocity, we get

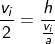
Rearranging the equation, we get

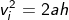
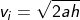
We can calculate the initial velocity when the final velocity is not zero. Consider the equation,

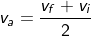
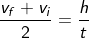
To above equation the substituting the value of t as

t=(v_f+v_i)/a

We get the equation as

(v_f+v_i) (v_f-v_i) = 2ah

The above equation can be written as

v_f²-v_i² = 2ah

Rearranging the terms to get initial velocity as

v_i² = v_f²– 2ah

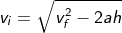
How to calculate velocity with height and time?

In vertical motion, the distance traveled by the body is equal to the height where the body begins to move.

The velocity can be calculated using height and time. The distance moved by the body with time always describes the body’s velocity. The physical entities such as acceleration and height also contribute to the finding the velocity.

We can calculate the velocity with height and time in three ways

By vertical motion of the body
By projectile motion of the body
By height vs. time graph

By vertical motion of the body

If the basketball is falling from the basket at height h, and is accelerating in the direction of gravity, then the velocity can be given as

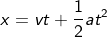
But the acceleration is given by

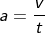
Substituting the value of a and replacing distance term as height h, we get

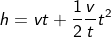
On rearranging the terms, the velocity with height and time is

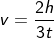
By Projectile motion

Consider another example; a basketball player shoots the ball to the basket standing at a distance d away from the basket. The ball makes the projectile motion to reach the basket; then we can calculate the velocity as follows:

The general expression of velocity is given by

v h 4 — Using Projectile motion picture illustrating how to find velocity with acceleration and height

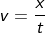
The ball travels a distance of d along with the height h; if we neglect the friction, distance can be written as

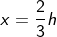
Substituting the value of x in the general equation of velocity, we get

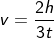
By height vs. time graph

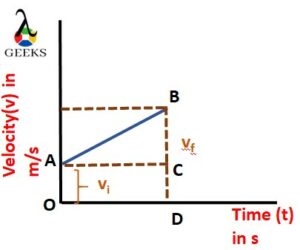
If we plot a graph with height in the y axis and time in the x-axis, the plot is called a height-time graph.

We can calculate the velocity from the height-time graph. The slope of the height-time graph gives the velocity of the body.

v h h vs t graph — Height Vs. Time graph to find velocity

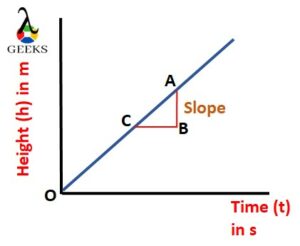
From the above graph, the slope is given by

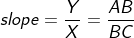
From the graph, AB is parallel to height h, and BC is parallel to time t; hence we can say that

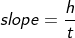
AB = h and BC = t;

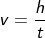
From the definition of velocity, we can say the slope is nothing but velocity. Thus the slope is equal to velocity.

How to find velocity with height and mass?

Though mass does not affect the velocity, it contributes the energy and force required to the body to attain a certain velocity.

The height and the mass are the entities associated with the object’s potential energy. Mass also contributes to the kinetic energy acquired by the object while moving. By knowing mass, let us understand how to find velocity with height.

The object at a certain height possesses potential, which makes the body move, and it is equal to the kinetic energy of the body while moving.

Since both potential energy and kinetic energy are equal, we can equate them.

E_p= E_k

The kinetic energy of the body is

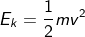
Rearranging the equation, we get

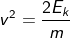
In the beginning, we have told that potential energy = kinetic energy,

Therefore the equation can be rewritten as

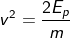
Generally, the potential energy is E_p= mgh.

The answer we got from potential energy can be substituted in the above equation to get the velocity of the body.

How to find velocity with height and gravity?

When you throw a stone in the air, it will fall back to the ground due to gravity. It is a general process. But have you observed that the speed of the ball? The speed of the stone while moving down is a little less than the speed of the same stone while it is falling back.

The above statement clarifies that velocity can vary due to gravity also. Gravity comes into action when a body is placed at a certain height; as gravity is an attractive force, it tries to bring the body at height towards the ground—so based on this data, how to find velocity with height and distance?

The earlier section discusses one way of finding the velocity with height and gravity. Let us discuss how to find velocity with height and distance by considering the kinematic equation of motion.

The height is always equal to the distance from the kinematic equation of distance. Hence we can consider the distance as height. So the equation will be

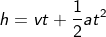
If the motion of the stone is in the direction of gravity, then the acceleration is only due to gravity; hence the equation can be rewritten as

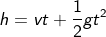
Rearranging the terms, the equation will be

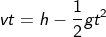
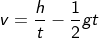
The above equation gives the velocity with height and gravity with the time factor. If the body is accelerating against gravity, then

g = -g

How to find velocity with height and angle?

When a body begins to fall from a certain height towards the surface, it makes some angle θ with the point of dropping. The angle made by the object helps us to find the answer for how to find velocity with height.

The displacement of the body in the vertical position is the height. The vertical component of velocity can be written as

v = v sinθ

If the body is making some horizontal displacement, then velocity is

v = v cosθ

From the equation of motion, the vertical and horizontal velocities can be written as

v_x = v cosθ

v_y = v sinθ-gt; where g is acceleration due to gravity

At maximum height, v_y= 0 = v sinθ –gt

v sinθ = gt

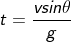
When a body is dropped at an angle θ and travels with velocity v, its range is given by

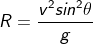
Therefore, using the value of R,

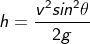
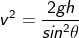
Therefore, the velocity can be rewritten as

Solved problems on how to calculate velocity with height

Problem 1) A ball is dropped from the height of 15m, and it reaches the ground with a certain velocity. Calculate the velocity of the ball.

Solution:

We are provided with only height h = 15m.

Since the ball moves towards the ground, the motion is due to acceleration due to gravity g. The value of acceleration due to gravity is g = 9.8 m/s². The velocity of the ball is

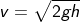
Substituting the values of h and g;

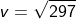
v = 17.14 m/s.

Problem 2) Calculate the initial velocity of the stone, which is falling from the height of 3m, and its acceleration is 2 m/s², and hence find the time taken by the stone to reach the ground.

Solution:

Given data: Height h = 3m

Acceleration of the stone a = 2 m/s².

The velocity of the stone is given by

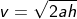
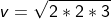
v = 3.46 m/s.

The time taken by the stone to reach the ground is given by the equation,

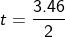
t = 1.79 s.

Problem 3) An object of mass 3 kg is dropped from the height of 7 m, accelerating due to gravity. Calculate the velocity of the object.

Solution:

The data are given –the mass of the object m = 3kg.

Height at which the object has dropped h = 7 m.

Acceleration due to gravity g = 9.8 m/s².

Since the object’s motion is due to mass, height, and gravity, so the work done is equal to potential energy. it is given by

E_p = mgh

The object is moving, so the object possesses kinetic energy; it is represented by the formula,

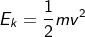
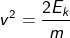
From the conservation of energy, when an object begins to move, its potential energy is now termed kinetic energy.

Therefore E_p= E_k

The potential energy is E_p = 3×9.8×7

E_p = 205.8 J

Substituting Ep = Ek = 205.8 J.

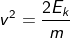
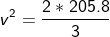
v² = 137.2

v = 11.71 m/s.

Problem 4) An athlete shoots a shot put in the air in the vertical direction, and it takes a time of 3 seconds to fall on the ground vertically from the height of 7 m from the ground. Calculate the velocity while the shot put is returning to earth.

Solution:

Given data – the height from the ground h = 7 m.

Time is taken to reach the ground = 3 seconds.

The velocity is given by

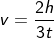
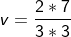
v = 2.33 m/s.

Problem 5) A body of mass 4 kg is dropped at the height of 11 meters above the ground by making an angle of 20°. Calculate the velocity of the body. (Take acceleration due to gravity as 10 m/s²)

Solution:

The data are given –the mass of the body m = 4 kg.

Height h = 11 m.

Angle θ = 20°.

Acceleration due to gravity g = 10 m/s².

The velocity is given by

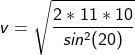
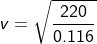
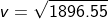
v = 43.45 m/s.

What is the formula to calculate velocity with height?

A: The formula to calculate velocity with height is v = √(2gh), where v is the velocity, g is the acceleration due to gravity, and h is the height.

How does calculus relate to finding velocity with height?

Derivatives: From Velocity to Acceleration

Velocity is a measure of how fast an object’s position changes over time. In calculus, we use the derivative to determine this rate of change. The derivative of an object’s position with respect to time gives us its velocity.

$v(t) = \frac{d}{dt}s(t)$

where:

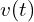$v(t)$ is the velocity as a function of time.
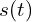$s(t)$ is the position as a function of time.
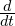$\frac{d}{dt}$ denotes the derivative with respect to time.

Acceleration: The Derivative of Velocity

Gravity affects the motion of objects by accelerating them at a constant rate towards the Earth. This acceleration (denoted as $g$ , approximately $9.81 m/s^2$ downward) is the rate of change of velocity. Using calculus, we express this as the derivative of velocity with respect to time.

$a(t) = \frac{d}{dt}v(t)$

For an object under only the influence of gravity, the acceleration is constant, so:

$a(t) = -g$

Integrals: From Acceleration to Velocity

If we know the acceleration, we can find the velocity by integrating the acceleration function. Since the acceleration due to gravity is constant, the integral of acceleration is a linear function of time:

$v(t) = \int a(t) , dt = \int -g , dt = -gt + C$

where $C$ is the integration constant, which can be determined if we know the initial velocity of the object.

Velocity and Height: The Integral Relationship

To relate velocity to height, we integrate the velocity function with respect to time, which gives us the position (height in this case) as a function of time.

$s(t) = \int v(t) , dt$

Substituting the expression for velocity we found by integrating the acceleration, we get:

$s(t) = \int (-gt + C) , dt = -\frac{1}{2}gt^2 + Ct + D$

Here, $D$ is another constant of integration, representing the initial height. By solving for these constants using initial conditions, we can fully determine the position function

What is free fall?

A: Free fall is the motion of an object under the influence of gravity alone. In free fall, the only force acting on the object is the force of gravity.

How can I calculate the height from which an object is dropped?

The formula to calculate the height ℎh from which an object is dropped without initial velocity is derived from the kinematic equation:

where:

ℎh is the height in meters (m),
g is the acceleration due to gravity (approximately 9.81 /29.81m/s2 on the surface of the Earth),
t is the time in seconds (s) it takes for the object to hit the ground.

If you have the time it took for the object to fall, you can simply plug the values into this equation to find the height. If you’re measuring the time it takes for an object to hit the ground, you can ignore air resistance for small heights and low speeds.

When calculating the height from which an object is dropped, we assume that it’s in free fall, which means the only force acting on it is gravity. The height can be calculated using the following kinematic equation:

$h = \frac{1}{2} g t^2$

In this formula:

ℎh represents the height from which the object is dropped (in meters, m).
g is the acceleration due to gravity, which is approximately 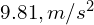$9.81 , m/s^2$ near the Earth’s surface.
t is the time in seconds (s) that it takes for the object to fall to the ground.

To find the height, simply measure the time from the moment the object is dropped until it hits the ground. Then, use that time in the formula above.

For example, if an object takes 3 seconds to hit the ground, the height from which it was dropped is calculated as follows:

$h = \frac{1}{2} \cdot 9.81 , m/s^2 \cdot (3 , s)^2$

$h = \frac{1}{2} \cdot 9.81 , m/s^2 \cdot 9 , s^2$

$h = \frac{1}{2} \cdot 9.81 \cdot 81$

$h = 4.905 \cdot 81$

$h = 397.305 , m$

So, the object was dropped from a height of approximately 397.305 meters.

How does height affect velocity?

A: The higher the object is, the greater its gravitational potential energy. As the object falls, this potential energy is converted into kinetic energy, leading to an increase in velocity.

What is the final velocity of an object that hits the ground?

A: The final velocity of an object that hits the ground is its velocity at impact. This velocity can be calculated using the formula v = √(2gh), where v is the final velocity, g is the acceleration due to gravity, and h is the height from which the object was dropped.

What role does gravity play in velocity with height?

A: Gravity is the force that pulls objects toward the center of the Earth. In the context of velocity with height, gravity is responsible for the acceleration of the object as it falls and increases its velocity.

How can I calculate the velocity of an object thrown vertically?

A: To calculate the velocity of an object thrown vertically, you can use the equation v = u + gt, where v is the final velocity, u is the initial speed, g is the acceleration due to gravity, and t is the time it takes for the object to reach its peak height.

Also Read:

How To Find Velocity With Acceleration And Distance:Different Approaches,Problems,Examples

January 20, 2024January 4, 2022 by Keerthi Murthi

In the kinematic theory, distance, velocity, acceleration, displacement, and time are the fundamental concepts to derive the equation of motion of in 2-dimensional space.

Generally, the distance traveled by a body per unit time gives the velocity. If the velocity changes with time during the motion, the body possesses the term acceleration. In this post, how velocity, acceleration, and distance are related is discussed in detail, and we get to know how to find velocity with acceleration and distance.

How to find velocity with acceleration and distance?

Suppose the body begins to move with initial velocity zero. The body is moving with acceleration ‘a’ and covers the distance ‘d’ meters; then, we need to find the velocity at which the body is moving. Now arise a question of how to find velocity with acceleration and distance?

Velocity gives how fast an object can move a distance over a given time period.

The expression is given by

v=x/t

But from the considering the equation

v = a*t

t=v/a

Substituting the value of t and rearranging, we get

v=x/(v/a)

v² = a*x

v=√ax

The equation obtained above is applicable if the body begins to move from zero velocity and then accelerates. The body is moving with constant acceleration to reach a distance d.

Using the general expression, we can find the body’s velocity with acceleration and distance with or without time.

how to find velocity with acceleration and distance — Image describing how to Velocity with Acceleration and Distance

How to find velocity from acceleration and distance without time?

The velocity of the body is always measured with the time taken by the body to travel a certain distance. If the time is not given by then, how to find velocity with acceleration and distance?

We follow two methods to find the velocity with given acceleration and distance. Generally, we consider the time in the very first equation; by eliminating the time factor, we get an equation of velocity without time.

By algebraic method:

To calculate the velocity without time, let us consider the equation of velocity with acceleration and time,

v = a * t

The ratio of distance traveled and time gives the velocity of the body. It is given by the equation,

v=x/t

Where x is the distance covered and t is the time taken to cover the distance d,

x/t=at

Substituting the value of v in the first equation; we get,

x = at²

From the kinematic theory, if the velocity of the body is changing with time, then we take the average of the velocity, therefore;

x= at²/2

But we can say that,t= v/a ,substituting in the above equation,

Solving and rearranging the terms we get,

x=v²/2a

v² = 2ax

v=√2ax

The above equation answers how to find velocity with acceleration and distance.

By integral calculus method:

The acceleration can be written as,

a=dv/dt

Velocity is nothing but the time derivative of distance covered by the body; it is given by,

dt=dx/v

Substituting the value of dt in the acceleration equation, we get

a=vdv/dx

a dx = v dv Since we have considered that the initial body possesses zero velocity, we integrate the above equation with the limit zero to a maximum value of the velocity and distance.

ax=v²/2

v² = 2 ax

v=√2ax

How to find velocity from acceleration and distance graph?

The plot of acceleration vs. distance gives the equation of motion under a specific time period.

The area under the acceleration–distance graph gives the square of the velocity of the moving body. From the definition of acceleration, it is the second-order derivative of the distance, so that the velocity will be two times the area.

vad graph 1 — Graph to show How to find velocity with acceleration and distance

For example, the acceleration displacement graph for a body moving with constant acceleration, after a certain time, the body decelerates and covers a certain distance, is given below, the velocity of the body can be calculated using the graph.

vad graph 2 — How to find velocity with acceleration and distance graph

The area covered by the a-d graph is a triangle; therefore, the area of the triangle is given by

A=1/2 hb

A=1/2 5*7

A = 17. 5 units

The velocity can be written as

A=√2*area

A=√35

Because 2A = 35 units.

v = 5.91 m/s.

How to find initial velocity from acceleration and distance?

Initial velocity is the velocity at which the body begins its motion.

In order to calculate the initial velocity, we have to consider the fundamental equation of the velocity; it is given by;

v=x/t

So the distance is given as; x = v*t

Here, the velocity is not constant; hence we can take the average value of the velocity as

v=v_i+v_f/2

So the equation will be

x=v_i+v_f/2t

But the equation of motion v_f = v_i + at, substituting the value of v_f, we get

x=v_i+(v_i+at)/2t

x=2v_i+at/2t

x=2v_i+a^t/2

2x = 2v_it+at²

On rearranging the above equation,

v_i = x/t – 1/2at

The above equation gives the initial velocity with acceleration and distance.

How to find final velocity from acceleration and distance?

The final velocity is the velocity attained by the body before the motion is stopped due to any hindrance.

When the moving body begins to accelerate means the velocity has been changed. This change in velocity is given by the initial and final velocity of the body. Suppose we have provided only initial velocity, then how to find velocity with acceleration and distance at the final point of the motion is answered below.

To derive the equation for final velocity, let us consider the motion of the car. The car is moving with initial velocity vi, and after some time t, the car begins to accelerate. The car attains the acceleration ‘a’ and covers the distance x.

The derivation can be done by three methods

By algebraic method
By calculus method
By graphical method

Let us study the above three methods in detail.

By algebraic method:

The distance traveled by the body is given by

x=v_i+v_f/2t

The velocity is not constant; it changes with the time period, so choose to take the average of the velocities.

From the kinematic equation of motion, we have

vf = vi + at

Let us rearrange the above equation to get the time as

t = v_f-v_i/2a

Substituting the value in the first equation,

x=v_f-v_i/2 v_f+v_i/a

The above equation is similar to (a+b)(a-b)= a²-b², then the required solution will be

x=v_f-v_i/2a

v_f²– v_i² = 2ax

v_f²= v_i² – 2ax

The equation obtained above is the required equation of final velocity. We can further simplify it by taking the square root on both sides; we get

v_f²=√(v_i²-2ax)

By calculus method:

We know that acceleration is given by the first-order derivative of velocity with respect to time t.

a=dv/dt

And the velocity as

v=dx/dt

Cross multiplying both equations and then integrating by choosing the limit x=0 to x=x and v=v_i to v=v_f we get;

v_f²– v_i² = 2ax

Rearranging the terms;

v_f²= v_i²– 2ax

By graphical method:

A plot of velocity vs. time can helps to find the final velocity of the body.

Generally the distance travelled by the body can be find finding the area covered by the body. Using these available data, we can calculate the distance traveled so that the equation of final velocity can be calculated.

vad graph 3 — How to find final velocity

From the above graph, the area of the trapezium OABD gives the distance traveled by the body,

x=OA+BD/2* OD

OA is the initial velocity vi, and BD is the Final velocity vf, and OD is the time, so the equation can be modified as,

x=v_f+v_i/2* t

But, we know that ]t = v_f-v_i/a

x=v_i+v_f/2* v_f-v_i/a

x=v_f²-v_i²/2a

v_f²– v_i² = 2ax

v_f²= v_i² – 2ax

The required equation of final velocity with the graphical method is obtained.

The final velocity equation from acceleration and distance can be rearranged to calculate the initial velocity of the body; it is shown below:

v_i²= v_f² – 2ax

How to find average velocity with acceleration and distance?

If the velocity keeps on changing, then we need to find the average velocity to describe the motion.

In order to establish an equation for average velocity, we must know initial and final velocity. But we can find average velocity even if the initial and final velocity is unknown by knowing acceleration and distance. Let us know how to find average velocity.

Let us suppose that a car is moving with initial velocity v_i and as it begins to accelerate after covering some distance x_i and travels a distance x_f at which it has the final velocity v_f.

The distance covered by the body is from xi to x_f, i.e., at the distance x_i, the velocity of the body is v_i, and at the point x_f, the velocity of the body is v_f, then.

A general expression of average velocity is given as,

v_a=v_i+v_f/2

Equation of motion for final velocity is v_f = v_i+ at

Substituting in the general equation, we have

v_a=v_i+v_i+at/2

v_a=2v_i+at/2

v_a=v_i+1/2 at

By considering the initial velocity expression, we get

v_i = x/t-1/2 at

v_a= x/t-1/2at+1/2 at

But t=√2x/a

Putting in the above expression, we get

v_a=x/√2x/a

Squaring on both sides, we get

v_a²=x²/2x/a

v_a²=ax²/2x

v_a²=ax/2

v_a=√ax/2

The above equation gives the average velocity of the moving body.

Solved Problems On How to find velocity with acceleration and distance

How to find velocity with acceleration and distance is given, if a motor vehicle is moving with a constant acceleration of 12 m/s² and covers a distance of 87 m, and hence find the time taken by the vehicle to cover the same distance.

Solution:

Given data – The distance covered by the vehicle x = 87 m.

Acceleration of the vehicle a = 12 m/s².

To find the velocity of the motor vehicle,

v=√ax

v=√12*87

v=√1044

v = 32.31 m/s.

From the relation between velocity, acceleration, distance, and time, we have the equation of velocity.

v= x/t

t= x/v

t= 87/32.31

t = 2.69 s.

In a race, the racer rides the bike with an initial velocity of 9 m/s. After time t, the velocity changes, and the acceleration is 3 m/s². The racer covers a distance of 10 m. calculate the final velocity of the bike to reach the given distance and hence find the average velocity of the bike.

Solution:

The equation to find the final velocity of the bike is given by;

v_f²= v_i² – 2ax

v_f²= (9)2 – 2(3 * 10)

v_f²= 81 – 60

v_f²= 21

v_f = 4.58 m/s.

The average velocity is given by

v_a=v_i+v_f/2

v_a=9+4.58/2

v_a=13.58/2

v = 6.79 m/s.

An athlete runs with an initial velocity of 10 m/s. He covers 10 m with a constant acceleration of 4 m/s². Find the initial velocity.

Solution:

Data are given for the calculation – the initial velocity v_i = 10 m/s.

Acceleration a = 4 m/s².

Distance x = 10 m

v_f²= v_i² – 2ax

v_f²= (10)² – 2( 4 *10)

v_f²= 100 – 80

v_f²= 20

v_f = 4.47 m/s.

Calculate the average velocity of particle moving with acceleration of 12 m/s² and the distance travelled by the particle is 26 meters.

Solution:

The formula gives the average velocity for given acceleration and distance.

v_a=√ax/2

The data are given – Acceleration of the particle a = 12 m/s².

Distance traveled by the particle x = 26 m.

Substituting the given values in the equation

√12*26/2

v_a=√156

v_a= 12.48 m/s.

A car travels a distance of 56 meters in 4 seconds. The acceleration of the car with the given time is 2 m/s². Calculate the initial velocity of the car.

Solution:

Given – the distance traveled by the car x = 56 m.

Time is taken by the car to cover the distance x t = 4 s.

Acceleration attain by the car a = 2 m/s².

The initial velocity of the car is given by the formula

v_i = x/t-1/2 at

Substituting the given values in the above equation,

v_i = 56/4-1/2*2*4

v_i = 14 – 4

v_i = 10 m/s.

A graph of acceleration and distance is plotted, then how to find velocity with acceleration and distance is given in the graph.

The distance traveled with acceleration given in the graph forms a trapezium, the area of the trapezium is given by

A=a+b/2* h

Where a and b are the adjacent side of the trapezium and h is the height.

From the above graph

a = 4.5 units

b = 9 units

h = 4 units

Substituting in the given equation,

A=(4.5+9/2)4

A = 27 units.

The velocity is given as

v=√2*area

v=√2*27

v=√56

v = 7.34 m/s.

How do you calculate displacement?

A: Displacement can be calculated using the equation s = ut + 1/2at^2, where s is the displacement, u is the initial velocity, a is the acceleration, and t is the time interval.

How do velocity and displacement relate in kinematics?

A: In kinematics, velocity and displacement are closely related. Velocity is the rate of change of displacement with respect to time. In other words, velocity represents the speed and direction of an object’s motion.

What is kinematics?

A: Kinematics is the branch of physics that deals with the motion of objects without considering the forces that cause the motion. It focuses on describing and analyzing the motion of objects using mathematical equations and concepts.

What happens when an object starts from rest?

A: When an object starts from rest, it means that its initial velocity is zero. In this case, the equation to find velocity simplifies to v = at, where v is the final velocity, a is the acceleration, and t is the time interval.

Also Read:

How To Find Velocity Without Time: Facts, Problems

January 20, 2024January 4, 2022 by AKSHITA MAPARI

Finding velocity without knowing the time may seem like a challenging task, but it is indeed possible. In this blog post, we will explore various methods to determine velocity without time. We will delve into the concept of velocity and understand why time is crucial in calculating it. We will also discuss special cases and common misconceptions related to finding velocity without time.

How to Find Velocity without Time

Understanding the Concept of Velocity

Before we dive into the methods of finding velocity without time, let’s first understand what velocity is. velocity is a vector quantity that measures the rate of change of an object‘s position with respect to time. It includes both the speed and direction of an object. Speed, on the other hand, is a scalar quantity that only measures the rate of change of distance traveled by an object.

The Importance of Time in Calculating Velocity

time plays a crucial role in calculating velocity. When we know the time taken by an object to travel a certain distance, we can easily determine its velocity using the formula:

$text{Velocity} = frac{text{Distance}}{text{Time}}$

However, there are situations where we may not have access to the time component, making it necessary to find velocity using alternative methods.

Methods to Determine Velocity without Time

Using Distance and Acceleration

One way to find velocity without time is by using the distance traveled and the acceleration of the object. If we know the initial and final velocities of the object, we can use the following formula:

$text{Velocity}^2 = text{Initial Velocity}^2 + 2 times text{Acceleration} times text{Distance}$

This equation is derived from the kinematic equation, (v^2 = u^2 + 2as), where (v) is the final velocity, (u) is the initial velocity, (a) is the acceleration, and (s) is the distance traveled.

Let’s consider an example to illustrate this method. Suppose an object starts from rest (initial velocity = 0) and undergoes constant acceleration of 5 m/s². If it travels a distance of 100 meters, we can find the velocity using the formula:

$text{Velocity}^2 = 0^2 + 2 times 5 times 100$

$text{Velocity}^2 = 1000$

$text{Velocity} = sqrt{1000}$

$text{Velocity} = 31.62 , text{m/s}$

In this example, we were able to find the velocity without knowing the time it took.

Using Initial and Final Velocity

Another method to find velocity without time is by using the initial and final velocities of the object. If we know the acceleration, we can use the following formula:

$text{Velocity} = frac{text{Final Velocity} - text{Initial Velocity}}{text{Time}}$

However, since we don’t have the value of time, we can modify the formula as follows:

$text{Velocity} = frac{text{Final Velocity} - text{Initial Velocity}}{text{Acceleration}}$

Let’s consider an example to illustrate this method. Suppose an object starts with an initial velocity of 10 m/s and undergoes constant acceleration of 2 m/s². If the final velocity is 30 m/s, we can find the velocity using the formula:

$text{Velocity} = frac{30 - 10}{2}$

$text{Velocity} = 10 , text{m/s}$

In this example, we were able to determine the velocity without knowing the time.

Using Angular Velocity and Acceleration

In certain cases involving rotational motion, we can find the velocity without time by using angular velocity and acceleration. Angular velocity measures the rate of change of angular displacement with respect to time. If we know the angular acceleration and the distance traveled, we can use the following formula:

$text{Velocity} = sqrt{2 times text{Acceleration} times text{Distance}}$

Let’s consider an example to illustrate this method. Suppose a wheel undergoes angular acceleration of 10 rad/s² and covers a distance of 5 revolutions. If we convert revolutions to radians (1 revolution = 2π radians), we can find the velocity using the formula:

$text{Velocity} = sqrt{2 times 10 times (5 times 2pi)}$

$text{Velocity} = sqrt{200pi}$

$text{Velocity} approx 25.13 , text{m/s}$

In this example, we were able to determine the velocity without knowing the time by utilizing angular velocity and acceleration.

Special Cases in Finding Velocity without Time

Image by Pradana Aumars – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

Finding Constant Velocity without Time

In the case of an object moving with constant velocity, the velocity remains the same throughout its motion. Therefore, if we know the initial velocity, we can directly use it as the velocity without the need for time. This applies to scenarios where there is no acceleration or the net acceleration is zero.

Finding Horizontal Velocity without Time

When an object is in projectile motion, its horizontal velocity remains constant throughout the motion. This means that even without knowing the time, we can use the initial horizontal velocity as the velocity of the object.

Finding Tangential Velocity without Time

In cases involving circular motion, tangential velocity is the velocity of an object traveling along the tangent to the circular path. If we know the radius of the circle and the angular velocity, we can find the tangential velocity without the need for time. The formula to calculate tangential velocity is:

$text{Tangential Velocity} = text{Angular Velocity} times text{Radius}$

How can I find the horizontal velocity without knowing the time?

If you are trying to determine the horizontal velocity of an object without knowing the time, you can use the concept of projectile motion. Projectile motion involves the motion of an object in the absence of external forces, where its motion in the vertical and horizontal directions are independent of each other. To find the horizontal velocity, you can use the equation v = d / t, where v represents the velocity, d is the horizontal distance traveled, and t is the time. By rearranging the formula as t = d / v, you can solve for time. However, if you desire to find the horizontal velocity without time, you can refer to the article “How to Find Horizontal Velocity”. It covers the necessary steps to calculate horizontal velocity using information such as the launch angle, initial velocity, and gravitational acceleration.

Common Misconceptions and Challenges in Finding Velocity without Time

How To Find Velocity Without Time: Facts, Problems 88

One common misconception is that velocity can always be determined without time. However, as we have seen, this is only possible when certain conditions are met, such as constant velocity, constant acceleration, or specific cases like projectile or circular motion. It is essential to understand the underlying concepts and apply the appropriate methods accordingly.

Another challenge in finding velocity without time arises when dealing with situations that don’t fall into the predefined categories. In such cases, it may be necessary to gather more information or use alternative approaches to determine the velocity accurately.

Finding velocity without knowing the time can be achieved through various methods, such as using distance and acceleration, initial and final velocity, or angular velocity and acceleration. It is crucial to understand the underlying concepts and apply the appropriate formulas accordingly. However, it is important to note that finding velocity without time is not always possible, and specific conditions must be met. By mastering these methods and understanding the limitations, we can effectively calculate velocity even in situations where time is unknown.

Also Read:

How to Find Momentum After Collision: Elastic, Inelastic, Formula and Problems

January 20, 2024December 30, 2021 by Manish Naik

The article discusses different formulas and problems on how to find momentum after collision.

An object’s velocity changes during a collision due to external force from another object. The velocity change causes a change in momentum after collision. So, we can find the momentum after collision using the impulse formula, laws of conservation of momentum, and conservation of energy.

The momentum before the collision is P_i =mu. The momentum after collision is also found by estimating a change in an object’s velocity v after the collision. P_f = mv

Read more about Momentum.

Suppose a stationary pull ball having a mass of 8kg is hit by another ball. After the collision, the ball is in motion at 5m/s. Determine the pool ball’s momentum after the collision.

**How to Find Momentum After Collision**

Given:

m = 8kg

v = 5m/s

To Find: ∆P =?

Formula:

∆P = P_f – P_i

Solution:

The momentum of ball after collision is calculated as,

∆P = P_f – P_i

∆P = mv – mu

Since pool ball at rest, i.e., u=0

∆P = mv

Substituting all values,

∆P = 8 x 5

∆P = 40

The pool ball’s momentum after collision is 40kg⋅m/s.

How to Find Momentum after Collision Formula?

The momentum after collision is determined using the impulse formula.

When we speak about finding momentum after collision of only one object, we can calculate it using the impulse formula. Impulse is the momentum change after collision due to the external force. Since collisions occur rapidly, it is tough to calculate the external force applied and time separately.

Once we computed momentum before P_i and after collision P_f, we can find impulse in terms of external force by another object as,

“Impulse (∆P) is the product of external force F and time difference (∆t) in which change in momentum occurs.”

What is Impulse — **Impulse – Change in Momentum**

Mathematically,

∆P = F ∆t

P_f – P_i = F ∆t

Read more about Types of Forces.

A football kicked the football having a mass of 5kg on the frictionless ground surface with a force of 30N over 5 sec. What is the velocity and momentum of football after kicking?

Given:

m = 5kg

F = 30N

∆t = 5 sec

To Find:

v₂=?
P_f=?

Formula:

P = mv
∆P = F ∆t

Solution:

The momentum of football before kicking is,

P_i = m₁v₁

Since football is at rest. i.e., v₁=0

Therefore, P_i = 0

The momentum of football before kicking is zero.

The momentum of football after kicking is calculated using the Impulse formula.

∆P = F ∆t

P_f-P_i = F ∆t

Since Pi = 0

P_f = F ∆t

Substituting all values,

P_f = 30 x 5

P_f = 150

The momentum of football after kicking is 150kg⋅m/s

The velocity of football after kicking is,

m₂v₂ = 150

v₂ = 150/5

v₂ = 30

The velocity of football after kicking is 30m/s.

How to Find Total Momentum of Two Objects after Collision?

The total momentum of two objects after collision is estimated using the law of conservation of momentum.

When two objects collide, their respective momentum changes because of their velocities, but their total momentum after collision remains the same. The total momentum after collision is summed by adding all the respective momentums of colliding objects.

In a closed or isolated system, when two objects holding different masses and velocities collide, they may move with each other or away, depending on the types of a collision – such as inelastic collision or elastic collision.

Types of Collision — **Elastic and Inelastic Collision**
(credit: shutterstock)

After the collision, their momentum, which is the product of their masses and velocities, is also varied. But when talking about the total momentum of an isolated system, it remains unchanged. During the collision, whatever momentum one object loses is gained by another object. That’s how the total momentum of colliding objects is conserved.

Suppose momentum of object 1 is P₁ = m₁u₁

Momentum of object 2 is P₂ = m₂u₂

Momentum of both objects before collision is P_i = P₁ + P₂ = m₁u₁ + m₂+u₂

If there is no net force involved during the collision, then momentum after collision Pf of both objects remains the same as before the collision.

Therefore, As per law of conservation of momentum,

P_i = P_f

m₁u₁ + m₂+u₂ = m₁v₁ + m₂+v₂ ……………………. (*)

Notice velocities of both objects changed after collision from u to v. That shows their respective momentum after collision also gets changed.

For an isolated system,

“The total momentum after collision is exactly as before collision as per the law of conservation of momentum.”

Suppose two marble pebbles having masses 10kg and 5kg moving at 8m/sec and 12 m/sec respectively; collide with each other. After the collision, both pebbles move away from each other with the same masses. If one pebble moves away with a velocity of 10m/sec, what is the second pebble’s velocity?

Given:

m₁ = 10kg

m₂ = 5kg

u₁= 8m/sec

u₂= 12m/sec

v₁= 10m/sec

To Find: v₂ =?

Formula:

m₁u₁ + m₂+u₂ = m₁v₁ + m₂+v₂

Solution:

The law of conservation of momentum calculates the velocity of the second pebble,

For isolated systems when no net force acts,

m₁u₁ + m₂+u₂ = m₁v₁ + m₂+v₂

Note that second objects move opposite to the first object. Therefore, the momentum of the second object must be negative.

Substituting all values,

10 x 8 + (- (5 x12) = 10 x 10 + (-(5xv2)

80 – 60 = 100 -5v2

5v₂ = 100 -20

v₂ = 80/5

v₂ = 16

The velocity of the second pebble after the collision is 16m/sec.

Read more about Relative Velocity.

How to Find Momentum after Elastic Collision?

The momentum after elastic collision is estimated using the law of conservation of energy.

The total momentum is conserved during the collision. The kinetic energy of a respective object may change after the collision, but the total kinetic energy after elastic collision stays the same. So, we can find momentum after elastic collision utilizing the law of conservation of energy.

Elastic collision

When the collision between objects is elastic, the total kinetic energy is conserved.

As per law of conservation of energy,

Rearranging equation (*) by terms with m1 on one side and terms with m2 on other.

Now rearranging equation (#) by terms with m1 on one side and the terms with m2 on other and cancel ½ common factor,

Recognize the first term on the left hand side is ‘1’ in the above equation, we get.

………………. (1)

Substitute above equation into equation (*), to eliminate v₂, we get

Finally rearrange above equation and solve for velocity v₁ of object 1 after collision,

Substitute above equation into equation (1) velocity v₂ of object 2 after collision,

Read more about Kinetic Energy.

When a 10kg ball moving at 2m/s elastically collides with another ball having mass 2kg oppositely moving at 4m/s. Calculate the final velocities of both balls after the elastic collision.

Given:

m₁ = 10kg

m₂ = 2kg

u₁ = 2m/s

u₂ = -4m/s

To Find:

v₁ =?
v₂ =?

Formula:

Solution:

The velocity of ball 1 after elastic collision is calculated as,

Substituting all values,

v₁ = 0

That means, the elastic collision stopped the ball 1.

The velocity of ball 2 after elastic collision is calculated as,

Substituting all values,

v₂= 6 m/s

That means the elastic collision changes the velocity of the second ball to 6m/s.

How to Find Momentum after Inelastic Collision?

The momentum after collision is determined using the law of conservation of momentum.

The total momentum is conserved during the collision. But the total kinetic energy of the system is also changed like the kinetic energy respective object, and the collision is said to be inelastic. So, we can find momentum after inelastic collision using the law of conservation of momentum.

**How to Find Momentum after Inelastic Collision?** (credit: shutterstock)

If the collision is elastic, both objects move away from each other with different velocities v₁, v₂ in opposite directions.

But if the collision is inelastic, both objects move with one final velocity V in the same direction.

Therefore, the momentum P_f after inelastic collision becomes m₁V + m₂V or V(m₁+m₂)

So, the equation of conservation of momentum for inelastic collision is,

m₁u₁ + m₂+u₂= V(m₁+m₂)

The formula for final velocity after inelastic collision is,

V=(m₁u₁ + m₂+u₂)/(m₁+m₂)

Read more about Speed.

Two boys are playing on the playground slide in the park. The first boy having a mass of 20kg sliding at 10m/s on the slide. Since the first boy becomes slower at certain portions latterly collides with another boy having a mass of 30kg who slides down at 12 m/s. What will be the velocity of both boys who slide down together after collision?

Given:

m₁ = 20kg

m₂ = 30kg

u₁ = 10m/s

u₂ = 12m/s

To Find: V =?

Formula:

V=(m₁u₁ + m₂+u₂)/(m₁+m₂)

Solution:

The final velocity of both boys sliding after collision is calculated as,

V=(m₁u₁ + m₂+u₂)/(m₁+m₂)

Substituting all values,

V = 11.2

The final velocity of both boys sliding after an inelastic collision is 11.2m/s.

Quick Facts

What is momentum and why is it important in collisions?

A: Momentum is a fundamental concept in physics that describes the motion of an object. It is calculated by multiplying an object’s mass by its velocity. In collisions, momentum is important because it determines how objects interact and how their motion changes.

What is the law of conservation of momentum?

A: The law of conservation of momentum states that the total momentum of a system of objects remains constant if no external forces act on it. This means that the total momentum before a collision is equal to the total momentum after the collision.

How do you calculate the momentum of an object?

A: The momentum of an object is calculated by multiplying its mass (in kilograms) by its velocity (in meters per second). The formula for momentum is: momentum = mass × velocity.

What are elastic and inelastic collisions?

Property	Elastic Collisions	Inelastic Collisions
Kinetic Energy	Conserved. Total kinetic energy before and after the collision is the same.	Not conserved. Total kinetic energy after the collision is less than before.
Momentum	Conserved. Total momentum before and after the collision remains constant.	Conserved. Total momentum before and after the collision remains constant, just as in elastic collisions.
Colliding Objects	Objects bounce off each other with no permanent deformation or generation of heat.	Objects may stick together or deform, generating heat and possibly sound or light.
Examples	Billiard balls colliding, an atom striking a perfectly rigid surface.	Car crashes, a lump of clay hitting a wall and sticking to it.
Energy Conversion	No conversion of kinetic energy into other forms of energy.	Kinetic energy is partially converted into other forms of energy, such as heat, sound, or potential energy (in the case of deformation).
Mathematical Complexity	Relatively simple to calculate final velocities using conservation laws.	More complex due to the need to consider energy dissipation and possible sticking together of objects.
Post-Collision Velocities	Can be calculated precisely using conservation laws.	Less predictable; it often requires additional information about the energy conversion and possible sticking.
Coefficient of Restitution	Equal to 1 (perfectly elastic).	Less than 1, indicating some energy loss.
Real-World Occurrence	Rare—most real-world collisions have some degree of inelasticity.	Common, as most collisions convert some kinetic energy into other forms.

Momentum in Elastic Collsion

Momentum in InElastic Collsion

What is the impulse-momentum theorem?

A: The impulse-momentum theorem states that the change in momentum of an object is equal to the applied impulse, which is the product of the force applied to the object and the time interval over which the force is applied.

What happens to the momentum of two objects in a collision?

A: In a collision between two objects, the momentum of the system is conserved. This means that the total momentum before the collision is equal to the total momentum after the collision. If the objects stick together after the collision, they move together with a combined momentum.

What is Newton’s third law and how does it relate to momentum?

A: Newton’s third law states that for every action, there is an equal and opposite reaction. In the context of collisions, this means that the forces exerted by the objects on each other are equal and opposite, resulting in a change in momentum for both objects.

How do you find the momentum after a collision?

A: To find the momentum after a collision, you need to calculate the final momentum of the system. This can be done by adding up the individual momenta of the objects involved in the collision. The formula for momentum is: momentum = mass × velocity.

What happens to the kinetic energy in a collision?

A: In general, the kinetic energy is not conserved in a collision. In an elastic collision, however, the kinetic energy is conserved, meaning that it remains the same before and after the collision. In an inelastic collision, some of the kinetic energy is lost as heat, sound, or deformation.

Is momentum conserved in all types of collisions?

A: Yes, momentum is conserved in all types of collisions. Whether it is an elastic or inelastic collision, the total momentum of the system before the collision is equal to the total momentum after the collision.

Also Read:

How To Find The Slope Of A Graph: Exhaustive Insights And Facts

January 20, 2024November 29, 2021 by Rabiya Khalid

Understanding how to find the slope of a graph is an essential skill in mathematics and physics. The slope of a graph represents the rate at which the dependent variable changes with respect to the independent variable. It tells us how steep or shallow a line or curve is. In this blog post, we will explore various methods to find the slope of a graph, including straight lines and curves. So let’s dive in!

How to Find the Slope of a Graph

Identifying the Rise and Run on a Graph

Before we can calculate the slope of a graph, we first need to understand the concepts of rise and run. Rise refers to the vertical change between two points on the graph, while run represents the horizontal change. The slope is then defined as the ratio of rise to run.

To identify the rise and run on a graph, choose two points on the line or curve. Let’s consider the following example:

Suppose we have a graph with two points, A(x₁, y₁) and B(x₂, y₂). The rise between these points is given by the difference in the y-coordinates: rise = y₂ – y₁. Similarly, the run is determined by the difference in the x-coordinates: run = x₂ – x₁.

Calculating the Slope of a Straight Line Graph

Calculating the slope of a straight line graph is relatively straightforward. We can use the formula:

$text{Slope} = frac{text{rise}}{text{run}} = frac{y₂ - y₁}{x₂ - x₁}$

Let’s work through an example to illustrate this:

Example: Find the slope of the line passing through the points (-2, 5) and (4, 9).

Solution: We can plug the values into the slope formula:

$text{Slope} = frac{9 - 5}{4 - (-2)} = frac{4}{6} = frac{2}{3}$

Therefore, the slope of the line is $frac{2}{3}$ .

Worked Out Examples on Finding the Slope of a Straight Line Graph

Let’s practice finding the slope of a straight line graph with a few more examples:

Example 1: Find the slope of the line passing through the points (-3, 2) and (1, 8).

Solution: Using the slope formula, we have:

$text{Slope} = frac{8 - 2}{1 - (-3)} = frac{6}{4} = frac{3}{2}$

Therefore, the slope of the line is $frac{3}{2}$ .

Example 2: Find the slope of the line passing through the points (2, 7) and (2, -3).

Solution: Here, we can observe that the x-coordinates of both points are the same. In such cases, the slope is undefined, as the run is zero. Therefore, the line is vertical, and its slope is undefined.

Finding the Slope of a Curve

Understanding the Concept of Slope for Curved Lines

Finding the slope of a curve requires a slightly different approach compared to straight lines. In the case of a curve, the slope at any point is given by the tangent line to the curve at that particular point. The tangent line represents the instantaneous rate of change at that point.

Techniques to Calculate the Slope of a Curve

Image by David Eppstein – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

To calculate the slope of a curve, we can use calculus and differentiate the equation of the curve with respect to the independent variable. The derivative, at any given point, represents the slope.

Let’s consider a simple example to illustrate this:

Example: Find the slope of the curve represented by the equation y = x² at the point (2, 4).

Solution: To find the slope at a point on a curve, we need to differentiate the equation with respect to x. In this case, differentiating y = x² gives us:

$frac{dy}{dx} = 2x$

Substituting x = 2 into the derivative:

$frac{dy}{dx} bigg|_{x=2} = 2(2) = 4$

Therefore, the slope of the curve at the point (2, 4) is 4.

Worked Out Examples on Finding the Slope of a Curve

Let’s solve a couple more examples to solidify our understanding of finding the slope of a curve:

Example 1: Find the slope of the curve represented by the equation y = 3x³ + 2x² – 5x + 6 at the point (1, 6).

Solution: Differentiating the equation y = 3x³ + 2x² – 5x + 6 with respect to x, we get:

$frac{dy}{dx} = 9x² + 4x - 5$

Substituting x = 1 into the derivative:

$frac{dy}{dx} bigg|_{x=1} = 9(1)² + 4(1) - 5 = 8$

Therefore, the slope of the curve at the point (1, 6) is 8.

Example 2: Find the slope of the curve represented by the equation y = sin(x) at the point (π/2, 1).

Solution: Taking the derivative of y = sin(x) with respect to x, we have:

$frac{dy}{dx} = cos(x)$

Substituting x = π/2 into the derivative:

$frac{dy}{dx} bigg|_{x=pi/2} = cos(pi/2) = 0$

Hence, the slope of the curve at the point (π/2, 1) is 0.

Special Cases in Finding the Slope of a Graph

how to find the slope of a graph — Image by TentativeTypist – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

Determining the Slope of a Horizontal Line

A horizontal line has the same y-coordinate at every point, meaning there is no vertical change (rise). Therefore, the slope of a horizontal line is always 0.

Determining the Slope of a Vertical Line

A vertical line has the same x-coordinate at every point, resulting in no horizontal change (run). In this case, the slope is undefined.

How to Handle Undefined and Zero Slopes

When the slope is undefined, it means the curve or line is vertical. When the slope is zero, it indicates a horizontal line. These special cases are important to note when analyzing a graph.

How is finding the slope of a graph related to finding average velocity in physics?

When studying the concepts of calculus and motion in physics, both finding the slope of a graph and calculating average velocity play important roles. By determining the slope of a graph, we can understand the rate of change of a variable over a given interval. This concept is closely related to velocity, which represents the rate at which an object changes its position. In physics, average velocity is calculated by dividing the change in position by the time taken. By understanding how to find the slope of a graph, we can gain insights into finding average velocity in physics. To learn more about the calculation of average velocity, please refer to the article on Finding average velocity in physics.

Numerical Problems on how to find the slope of a graph

Problem 1

Find the slope of the line passing through the points (2, 4) and (5, 10).

Solution:

To find the slope of a line passing through two points, we can use the formula:

$text{Slope} = frac{{text{change in } y}}{{text{change in } x}}$

Given the points (2, 4) and (5, 10), we can calculate the change in y and change in x as follows:

$text{change in } y = 10 - 4 = 6$

$text{change in } x = 5 - 2 = 3$

Substituting these values into the slope formula:

$text{Slope} = frac{6}{3} = 2$

Therefore, the slope of the line passing through the points (2, 4) and (5, 10) is 2.

Problem 2

Determine the slope of the line that passes through the points (3, -1) and (7, 5).

Solution:

Using the slope formula:

$text{Slope} = frac{{text{change in } y}}{{text{change in } x}}$

We can calculate the change in y and change in x:

$text{change in } y = 5 - (-1) = 6$

$text{change in } x = 7 - 3 = 4$

Substituting these values into the slope formula:

$text{Slope} = frac{6}{4} = frac{3}{2}$

Hence, the slope of the line passing through the points $3, -1) and (7, 5) is (frac{3}{2}$ .

Problem 3

Find the slope of the line that passes through the points (-2, -3) and (4, 1).

Solution:

By using the slope formula:

$text{Slope} = frac{{text{change in } y}}{{text{change in } x}}$

We can calculate the change in y and change in x:

$text{change in } y = 1 - (-3) = 4$

$text{change in } x = 4 - (-2) = 6$

Substituting these values into the slope formula:

$text{Slope} = frac{4}{6} = frac{2}{3}$

Therefore, the slope of the line passing through the points $-2, -3) and (4, 1) is (frac{2}{3}$ .

Also Read:

How To Find Slope Of Position Time Graph: Exhaustive Insights And Facts

January 20, 2024November 25, 2021 by Rabiya Khalid

How to Find the Slope of a Position Time Graph

In physics, slope refers to the steepness or incline of a line on a graph. It measures how much one variable changes in relation to another variable. In the context of a position-time graph, the slope represents the rate at which an object’s position changes over time.

The Relationship between Position and Time

A position-time graph is a graphical representation that shows how the position of an object changes over time. The position is usually plotted on the vertical axis, while time is plotted on the horizontal axis. By analyzing the graph, we can determine the object’s motion, direction, and velocity.

The Importance of Slope in Position Time Graphs

The slope of a position-time graph provides valuable information about an object’s motion. It indicates the object’s velocity at a specific point in time. A positive slope indicates motion in the positive direction, while a negative slope indicates motion in the negative direction. A horizontal line with zero slope represents a stationary object.

Calculating the Slope of a Position Time Graph

Image by MikeRun – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY-SA 4.0.

Step-by-Step Guide to Finding the Slope

To calculate the slope of a position-time graph, we need to find the change in position and the change in time between two points on the graph. The slope is determined by dividing the change in position by the change in time.

Let’s consider two points on the graph, Point A with coordinates (t1, x1) and Point B with coordinates (t2, x2). The slope can be calculated using the formula:

$slope = \frac{{x2 - x1}}{{t2 - t1}}$

The Role of Units in Calculating Slope

When calculating the slope of a position-time graph, it is crucial to consider the units of measurement. The units of position are usually meters (m), while time is typically measured in seconds (s). To obtain an accurate slope value, ensure that both the position and time values are in the correct units.

Common Mistakes to Avoid When Calculating Slope

When calculating the slope of a position-time graph, it is essential to avoid common mistakes. Some common errors include:

Switching the order of the coordinates when using the slope formula.
Not converting the position and time values to the correct units.
Using the wrong formula or equation to calculate the slope.

To prevent these mistakes, double-check your calculations and ensure that you have correctly followed the steps outlined in the guide.

Practical Examples of Finding the Slope on a Position Time Graph

Example Problem 1: Simple Position Time Graph

Let’s consider a position-time graph where the object starts at position 2 meters at time 0 seconds and moves to position 8 meters at time 4 seconds. To find the slope, we can use the formula:

$slope = \frac{{8 - 2}}{{4 - 0}} = \frac{{6}}{{4}} = 1.5$

The slope of the graph is 1.5, indicating that the object is moving at a constant velocity of 1.5 meters per second.

Example Problem 2: Complex Position Time Graph

Now let’s consider a more complex position-time graph. Suppose an object starts at position 0 meters at time 0 seconds and moves to position 10 meters at time 5 seconds. Then, it changes direction and moves back to position 5 meters at time 10 seconds. To calculate the slope, we can divide the change in position by the change in time for each segment of the graph.

For the first segment from 0 to 5 seconds:

$slope = \frac{{10 - 0}}{{5 - 0}} = \frac{{10}}{{5}} = 2$

For the second segment from 5 to 10 seconds:

$slope = \frac{{5 - 10}}{{10 - 5}} = \frac{{-5}}{{5}} = -1$

The slope of the first segment is 2, indicating motion in the positive direction, while the slope of the second segment is -1, indicating motion in the negative direction.

Example Problem 3: Position Time Graph with Multiple Slopes

Consider a position-time graph where an object starts at position 2 meters at time 0 seconds. It then moves to position 8 meters at time 4 seconds and stays at that position until time 8 seconds. Finally, it moves back to position 2 meters at time 12 seconds. To calculate the slope, we divide the change in position by the change in time for each segment of the graph.

For the first segment from 0 to 4 seconds:

$slope = \frac{{8 - 2}}{{4 - 0}} = \frac{{6}}{{4}} = 1.5$

For the second segment from 4 to 8 seconds:

$slope = \frac{{8 - 8}}{{8 - 4}} = \frac{{0}}{{4}} = 0$

For the third segment from 8 to 12 seconds:

$slope = \frac{{2 - 8}}{{12 - 8}} = \frac{{-6}}{{4}} = -1.5$

The slope of the first segment is 1.5, indicating motion in the positive direction. The slope of the second segment is 0, indicating a stationary object. The slope of the third segment is -1.5, indicating motion in the negative direction.

How can understanding the slope of a position-time graph help in analyzing motion?

Understanding the slope of position-time graphs is crucial in analyzing motion. By studying the rate at which an object’s position changes over time, we can determine important properties such as velocity and acceleration. The article on LambdaGeeks.com titled Understanding the slope of position-time provides detailed insights into the concept. By internal linking, we can gain a deeper understanding of how the slope of a position-time graph relates to the object’s motion and its implications.

The Relationship between Slope and Velocity

Understanding Velocity in Physics

Velocity is a measure of an object’s speed in a given direction. It indicates how fast an object is moving and in which direction it is moving. In physics, velocity is often represented by the symbol ‘v’ and is measured in meters per second (m/s).

How Slope Represents Velocity on a Position Time Graph

On a position-time graph, the slope represents the object’s velocity at a particular point in time. If the slope is positive, it indicates that the object is moving in the positive direction. If the slope is negative, it indicates that the object is moving in the negative direction. The steeper the slope, the greater the velocity.

The Difference between Positive and Negative Slopes

A positive slope on a position-time graph indicates that the object is moving in the positive direction, while a negative slope indicates motion in the negative direction. A zero slope represents a stationary object. The magnitude of the slope indicates the object’s velocity. A steeper slope indicates a higher velocity, while a shallower slope indicates a lower velocity.

To summarize, the slope of a position-time graph is a crucial concept in physics. It allows us to determine an object’s velocity, direction, and motion. By understanding the relationship between slope and velocity, we can analyze and interpret position-time graphs effectively. Remember to follow the step-by-step guide for calculating the slope, pay attention to the units, and avoid common mistakes. With practice, you’ll become adept at finding the slope of position-time graphs and interpreting their meaning in the context of physics.

Also Read:

How to find instantaneous velocity from average velocity: Detailed Insights

January 20, 2024November 24, 2021 by Raghavi Acharya

instantaneous velocity from average velocity 0

How to Find Instantaneous Velocity from Average Velocity

instantaneous velocity from average velocity 1

Velocity is an important concept in physics that measures how fast an object is moving and in which direction. It plays a crucial role in understanding the motion of objects and calculating various other quantities such as acceleration, displacement, and momentum. In this blog post, we will explore the relationship between average velocity and instantaneous velocity, and learn how to find instantaneous velocity from average velocity.

How to Calculate Average Velocity

Average velocity is defined as the displacement of an object divided by the time it takes for that displacement to occur. It gives us a measure of the overall change in position of an object over a specific time interval. The formula for average velocity is:

$v_{avg} = frac{Delta x}{Delta t}$

where $v_{avg}$ represents the average velocity, $Delta x$ represents the change in position, and $Delta t$ represents the change in time.

To calculate average velocity, simply subtract the initial position from the final position and divide it by the time interval. For example, if an object travels a distance of 100 meters in a time of 20 seconds, the average velocity can be calculated as:

$v_{avg} = frac{100 , text{m}}{20 , text{s}} = 5 , text{m/s}$

How to Determine Instantaneous Velocity

instantaneous velocity from average velocity 3

While average velocity gives us an overall measure of an object’s motion over a specific time interval, instantaneous velocity provides us with information about the object’s motion at a specific point in time. It is the velocity of an object at an exact moment or instant. To determine instantaneous velocity, we need to consider the concept of limit.

The Concept of Limit in Calculating Instantaneous Velocity

The concept of limit involves finding the value that a function approaches as the input approaches a certain value. In the context of instantaneous velocity, we want to find the velocity of an object at a particular moment, which corresponds to an infinitesimally small time interval. By taking smaller and smaller time intervals, we can approximate the instantaneous velocity.

The Formula for Instantaneous Velocity

Instantaneous velocity can be calculated using calculus, specifically by taking the derivative of the position function with respect to time. In mathematical terms, the formula for instantaneous velocity is:

$v(t) = lim_{Delta t to 0} frac{Delta x}{Delta t}$

where $v(t)$ represents the instantaneous velocity at time $t$ , $Delta x$ represents the change in position, and $Delta t$ represents the change in time. Taking the limit as $Delta t$ approaches zero allows us to calculate the velocity at an exact moment.

Worked out Example on Instantaneous Velocity Calculation

Let’s consider an example to better understand how to find instantaneous velocity from average velocity. Suppose an object is moving along a straight line, and its position at time $t$ is given by the equation $x(t) = 3t^2 + 2t + 1$ . We want to find the instantaneous velocity at $t = 2$ seconds.

To find the instantaneous velocity, we need to take the derivative of the position function with respect to time:

$v(t) = frac{d}{dt} (3t^2 + 2t + 1)$

Using the power rule of differentiation, we can differentiate each term of the equation:

$v(t) = 6t + 2$

Now, we can substitute $t = 2$ into the equation to find the instantaneous velocity at that moment:

$v(2) = 6(2) + 2 = 14 , text{m/s}$

Therefore, the instantaneous velocity at $t = 2$ seconds is $14 , text{m/s}$ .

Comparing Instantaneous Velocity and Average Velocity

Instantaneous velocity and average velocity are related but represent different aspects of an object’s motion.

Situations when Instantaneous Velocity equals Average Velocity

In certain cases, the instantaneous velocity and average velocity of an object can be equal. This occurs when the object is moving at a constant velocity over a specific time interval. For example, if a car travels at a constant speed of $50 , text{km/h}$ for $2 , text{hours}$ , the average velocity over the entire time interval would be $50 , text{km/h}$ . Since the car maintains a constant velocity, the instantaneous velocity at any point during the $2 , text{hours}$ would also be $50 , text{km/h}$ .

Practical Examples Illustrating the Comparison

To further illustrate the difference between instantaneous velocity and average velocity, let’s consider a couple of practical examples.

Example 1: A car travels at a speed of $60 , text{km/h}$ for $1 , text{hour}$ . During the first $30 , text{minutes}$ , it maintains a constant velocity of $60 , text{km/h}$ . However, during the second $30 , text{minutes}$ , it comes to a complete stop and remains stationary. In this case, the average velocity over the entire $1 , text{hour}$ would still be $60 , text{km/h}$ , but the instantaneous velocity during the first $30 , text{minutes}$ would be $60 , text{km/h}$ and during the second $30 , text{minutes}$ would be $0 , text{km/h}$ .

Example 2: A ball is thrown upwards with an initial velocity of $20 , text{m/s}$ . As it rises, its velocity gradually decreases until it reaches its peak height and starts falling back down. At the highest point, the ball momentarily comes to a stop before accelerating downwards. In this case, the average velocity over the entire trajectory would be $0 , text{m/s}$ since the ball starts and ends at the same height with the same velocity. However, the instantaneous velocity would be positive during the ascent, $0 , text{m/s}$ at the highest point, and negative during the descent.

Understanding the relationship between average velocity and instantaneous velocity is crucial for analyzing the motion of objects. By calculating average velocity, we can determine the overall change in position over a specific time interval. To find instantaneous velocity, we need to consider the concept of limit and take the derivative of the position function with respect to time. It is important to remember that instantaneous velocity provides information about an object’s motion at an exact moment, while average velocity gives an overall measure of its motion over a specific interval.

What is the difference between instantaneous velocity and average velocity? Provide insight into the content of the article Difference between instantaneous velocity and average velocity.

The difference between instantaneous velocity and average velocity is explored in detail in the article Difference between instantaneous velocity and average velocity. Instantaneous velocity refers to the velocity of an object at a specific moment in time, while average velocity is the total displacement of an object divided by the total time taken. The article further delves into the calculation methods, applications, and significance of these two concepts in physics. By understanding the difference between instantaneous velocity and average velocity, one can gain a comprehensive understanding of how velocity is measured and analyzed.

Numerical Problems on how to find instantaneous velocity from average velocity

instantaneous velocity from average velocity 2

Problem 1:

A car travels along a straight road for 4 hours and covers a distance of 320 km. Find the instantaneous velocity at the end of the second hour if the average velocity during the first 3 hours is 80 km/hr.

Solution:

Let’s assume that the instantaneous velocity at the end of the second hour is $v_2$ km/hr.

The average velocity during the first 3 hours is given by:

$v_{text{avg}} = frac{text{Total distance}}{text{Total time}}$

Substituting the given values, we have:

$80 , text{km/hr} = frac{320 , text{km}}{3 , text{hours}}$

Solving the above equation, we find that the total distance covered in the first 3 hours is 240 km.

To find the instantaneous velocity at the end of the second hour, we need to determine the distance covered in the second hour. Since the car has covered a total distance of 240 km in the first 3 hours, the distance covered in the second hour is given by:

$240 , text{km} - 80 , text{km/hr} times 2 , text{hours} = 80 , text{km}$

Therefore, the instantaneous velocity at the end of the second hour is 80 km/hr.

Problem 2:

A cyclist covers a distance of 150 km in 5 hours. Find the instantaneous velocity after 3 hours if the average velocity during the first 4 hours is 40 km/hr.

Solution:

Let’s assume that the instantaneous velocity after 3 hours is $v_3$ km/hr.

The average velocity during the first 4 hours is given by:

$v_{text{avg}} = frac{text{Total distance}}{text{Total time}}$

Substituting the given values, we have:

$40 , text{km/hr} = frac{150 , text{km}}{4 , text{hours}}$

Solving the above equation, we find that the total distance covered in the first 4 hours is 160 km.

To find the instantaneous velocity after 3 hours, we need to determine the distance covered in the third hour. Since the cyclist has covered a total distance of 160 km in the first 4 hours, the distance covered in the third hour is given by:

$160 , text{km} - 40 , text{km/hr} times 3 , text{hours} = 40 , text{km}$

Therefore, the instantaneous velocity after 3 hours is 40 km/hr.

Problem 3:

A train covers a distance of 600 km in 8 hours. Find the instantaneous velocity after 6 hours if the average velocity during the first 5 hours is 70 km/hr.

Solution:

Let’s assume that the instantaneous velocity after 6 hours is $v_6$ km/hr.

The average velocity during the first 5 hours is given by:

$v_{text{avg}} = frac{text{Total distance}}{text{Total time}}$

Substituting the given values, we have:

$70 , text{km/hr} = frac{600 , text{km}}{5 , text{hours}}$

Solving the above equation, we find that the total distance covered in the first 5 hours is 350 km.

To find the instantaneous velocity after 6 hours, we need to determine the distance covered in the sixth hour. Since the train has covered a total distance of 350 km in the first 5 hours, the distance covered in the sixth hour is given by:

$350 , text{km} - 70 , text{km/hr} times 5 , text{hours} = 50 , text{km}$

Therefore, the instantaneous velocity after 6 hours is 50 km/hr.

Also Read:

How to Find Time with Acceleration and Distance: A Comprehensive Guide

June 18, 2024October 3, 2021 by Shambhu Patil

Summary

To find the time taken for an object to travel a certain distance with a given acceleration, you can use the formula: t = √((2d)/a) - (v₀/a), where t is the time, d is the distance, a is the acceleration, and v₀ is the initial velocity. If the initial velocity is zero, the formula simplifies to t = √((2d)/a). This guide will provide a detailed explanation of the formula, its derivation, and practical examples to help you master the concept of finding time with acceleration and distance.

Understanding the Formula

The formula to find time with acceleration and distance is derived from the equations of motion, which describe the relationship between an object’s position, velocity, and acceleration over time. The formula is:

t = √((2d)/a) - (v₀/a)

Where:
– t is the time (in seconds)
– d is the distance (in meters)
– a is the acceleration (in meters per second squared)
– v₀ is the initial velocity (in meters per second)

If the initial velocity is zero, the formula simplifies to:

t = √((2d)/a)

This formula assumes that the acceleration is constant throughout the motion, which is often the case in physics problems.

Derivation of the Formula

The formula can be derived from the equations of motion, which are:

v = v₀ + at
d = v₀t + (1/2)at²

Rearranging the second equation, we get:

t = √((2d)/a) - (v₀/a)

This is the formula for finding the time with acceleration and distance.

Assumptions and Limitations

The formula assumes that:
– The acceleration is constant throughout the motion.
– The initial velocity is known or can be assumed to be zero.

If these assumptions are not met, the formula may not provide accurate results. In such cases, you may need to use more complex equations of motion or numerical methods to find the time.

Practical Examples

Let’s consider some practical examples to illustrate the use of the formula.

Example 1: Calculating Time with Constant Acceleration

Suppose an object is traveling a distance of 1,000,000 meters with a constant acceleration of 10 meters per second squared, and the initial velocity is zero.

Using the formula:
t = √((2d)/a)
t = √((2 × 1,000,000)/10)
t = 632.46 seconds

Therefore, the time taken for the object to travel 1,000,000 meters with a constant acceleration of 10 meters per second squared and an initial velocity of zero is 632.46 seconds.

Example 2: Calculating Time with Non-zero Initial Velocity

Now, let’s consider a scenario where the initial velocity is not zero.

Suppose an object is traveling a distance of 500 meters with a constant acceleration of 5 meters per second squared, and the initial velocity is 20 meters per second.

Using the formula:
t = √((2d)/a) - (v₀/a)
t = √((2 × 500)/5) - (20/5)
t = 10 seconds - 4 seconds
t = 6 seconds

Therefore, the time taken for the object to travel 500 meters with a constant acceleration of 5 meters per second squared and an initial velocity of 20 meters per second is 6 seconds.

Example 3: Calculating Time with Varying Acceleration

In some cases, the acceleration may not be constant throughout the motion. Let’s consider an example where the acceleration varies.

Suppose an object is traveling a distance of 1,000 meters with an initial velocity of 10 meters per second. The acceleration starts at 5 meters per second squared for the first 500 meters, and then changes to 10 meters per second squared for the remaining 500 meters.

In this case, you would need to split the motion into two parts and use the formula for each part separately. The total time would be the sum of the times for the two parts.

For the first 500 meters:
t₁ = √((2 × 500)/5) - (10/5)
t₁ = 10 seconds - 2 seconds
t₁ = 8 seconds

For the remaining 500 meters:
t₂ = √((2 × 500)/10) - (18/10) (where 18 is the final velocity from the first part)
t₂ = 5 seconds - 1.8 seconds
t₂ = 3.2 seconds

The total time is the sum of the two parts:
t = t₁ + t₂
t = 8 seconds + 3.2 seconds
t = 11.2 seconds

Therefore, the total time taken for the object to travel 1,000 meters with varying acceleration is 11.2 seconds.

Conclusion

In this comprehensive guide, we have explored the formula for finding time with acceleration and distance, its derivation, and practical examples to help you understand the concept better. Remember, the formula assumes constant acceleration and known initial velocity, and if these assumptions are not met, you may need to use more complex equations or numerical methods to find the time.

By mastering the use of this formula, you will be able to solve a wide range of physics problems involving motion and time, which is essential for students and professionals in various scientific and engineering fields.

Reference:

How to Find the Magnitude of Acceleration: A Comprehensive Guide

June 18, 2024September 21, 2021 by Alpa P. Rajai

Acceleration is a fundamental concept in physics, describing the rate of change in an object’s velocity over time. Determining the magnitude of acceleration is crucial in various fields, from engineering and robotics to aerospace and sports science. In this comprehensive guide, we will explore three primary methods to calculate the magnitude of acceleration, providing you with a deep understanding and practical applications.

1. Newton’s Second Law: Relating Force, Mass, and Acceleration

According to Newton’s second law of motion, the acceleration (a) of an object is directly proportional to the net force (F) acting on it and inversely proportional to the object’s mass (m). Mathematically, this relationship can be expressed as:

a = F/m

where the bolded symbols represent vectors, and the vertical lines denote the magnitude of the vector, which is always positive (or equals zero).

To use this method, you need to know the net force acting on the object and its mass. Once you have these values, you can simply plug them into the equation and solve for the magnitude of acceleration.

Example: If a force of 50 N is acting on an object with a mass of 100 kg, the magnitude of acceleration can be calculated as:

a = F/m
a = 50 N / 100 kg
a = 0.5 m/s²

In this case, the magnitude of acceleration is 0.5 m/s².

2. Summing Up the Acceleration Components

Acceleration is a vector quantity, meaning it has both magnitude and direction. To find the magnitude of acceleration, you can sum up the components of the acceleration vector.

In a Cartesian coordinate system, the acceleration vector can be broken down into its x and y components (ax and ay). If you are working with circular motion, the acceleration vector can be decomposed into tangential (at) and centripetal (ac) components.

Regardless of the coordinate system, the magnitude of acceleration can be calculated using the following formulas:

|a| = √(ax² + ay²)    (for 2-D space)
|a| = √(ax² + ay² + az²)    (for 3-D space)

where |a| represents the magnitude of the acceleration vector.

Example: Suppose an object is moving in a 2-D plane, and its acceleration components are ax = 2 m/s² and ay = 3 m/s². The magnitude of acceleration can be calculated as:

|a| = √(ax² + ay²)
|a| = √(2² + 3²)
|a| = √(4 + 9)
|a| = √13 m/s²

In this case, the magnitude of acceleration is approximately 3.61 m/s².

3. Calculating Acceleration from Velocity Change

Acceleration is the rate of change in an object’s velocity. If you know the initial velocity (v0) and the final velocity (v1) of an object, as well as the time interval (Δt) over which the velocity change occurred, you can calculate the magnitude of acceleration using the following formula:

a = (v1 - v0) / Δt

This method is particularly useful when you have information about the object’s velocities and the time interval, but not the forces or masses involved.

Example: Suppose an object’s initial velocity is 10 m/s, and its final velocity is 20 m/s, with a time interval of 2 seconds. The magnitude of acceleration can be calculated as:

a = (v1 - v0) / Δt
a = (20 m/s - 10 m/s) / 2 s
a = 10 m/s / 2 s
a = 5 m/s²

In this case, the magnitude of acceleration is 5 m/s².

Additional Considerations and Applications

Accelerometers: Accelerometers are devices that measure the acceleration of an object. They are widely used in various applications, such as smartphones, fitness trackers, and inertial navigation systems.
Circular Motion: When an object is moving in a circular path, the acceleration can be decomposed into tangential and centripetal components. The magnitude of the acceleration vector in this case is the vector sum of the tangential and centripetal accelerations.
Rotational Motion: For objects undergoing rotational motion, the magnitude of the angular acceleration can be used to calculate the linear acceleration at a specific point on the object.
Numerical Problems: Solving numerical problems involving the magnitude of acceleration can help you develop a deeper understanding of the concepts and their practical applications.

Conclusion

Determining the magnitude of acceleration is a fundamental skill in physics and engineering. By mastering the three primary methods discussed in this guide – Newton’s second law, summing up the acceleration components, and calculating acceleration from velocity change – you will be equipped to solve a wide range of problems involving the motion of objects. Remember to practice applying these methods to various scenarios, as hands-on experience is key to developing a strong grasp of this important concept.

How to find velocity with Height?

How to find velocity with acceleration and height?

How to find initial velocity with acceleration and height?

How to calculate velocity with height and time?

How to find velocity with height and mass?

How to find velocity with height and gravity?

How to find velocity with height and angle?

Solved problems on how to calculate velocity with height

Problem 1) A ball is dropped from the height of 15m, and it reaches the ground with a certain velocity. Calculate the velocity of the ball.

Problem 2) Calculate the initial velocity of the stone, which is falling from the height of 3m, and its acceleration is 2 m/s2, and hence find the time taken by the stone to reach the ground.

Problem 3) An object of mass 3 kg is dropped from the height of 7 m, accelerating due to gravity. Calculate the velocity of the object.

Problem 4) An athlete shoots a shot put in the air in the vertical direction, and it takes a time of 3 seconds to fall on the ground vertically from the height of 7 m from the ground. Calculate the velocity while the shot put is returning to earth.

Problem 5) A body of mass 4 kg is dropped at the height of 11 meters above the ground by making an angle of 20°. Calculate the velocity of the body. (Take acceleration due to gravity as 10 m/s2)

What is the formula to calculate velocity with height?

How does calculus relate to finding velocity with height?

What is free fall?

How can I calculate the height from which an object is dropped?

How does height affect velocity?

What is the final velocity of an object that hits the ground?

What role does gravity play in velocity with height?

How can I calculate the velocity of an object thrown vertically?

How to find velocity with acceleration and distance?

How to find velocity from acceleration and distance without time?

How to find velocity from acceleration and distance graph?

How to find initial velocity from acceleration and distance?

How to find final velocity from acceleration and distance?

How to find average velocity with acceleration and distance?

Solved Problems On How to find velocity with acceleration and distance

How to find velocity with acceleration and distance is given, if a motor vehicle is moving with a constant acceleration of 12 m/s2 and covers a distance of 87 m, and hence find the time taken by the vehicle to cover the same distance.

In a race, the racer rides the bike with an initial velocity of 9 m/s. After time t, the velocity changes, and the acceleration is 3 m/s2. The racer covers a distance of 10 m. calculate the final velocity of the bike to reach the given distance and hence find the average velocity of the bike.

An athlete runs with an initial velocity of 10 m/s. He covers 10 m with a constant acceleration of 4 m/s2. Find the initial velocity.

Calculate the average velocity of particle moving with acceleration of 12 m/s2 and the distance travelled by the particle is 26 meters.

A car travels a distance of 56 meters in 4 seconds. The acceleration of the car with the given time is 2 m/s2. Calculate the initial velocity of the car.

A graph of acceleration and distance is plotted, then how to find velocity with acceleration and distance is given in the graph.

How do you calculate displacement?

How do velocity and displacement relate in kinematics?

What is kinematics?

What happens when an object starts from rest?

How to Find Velocity without Time

Understanding the Concept of Velocity

The Importance of Time in Calculating Velocity

Methods to Determine Velocity without Time

Using Distance and Acceleration

Using Initial and Final Velocity

Using Angular Velocity and Acceleration

Special Cases in Finding Velocity without Time

Finding Constant Velocity without Time

Finding Horizontal Velocity without Time

Finding Tangential Velocity without Time

How can I find the horizontal velocity without knowing the time?

Common Misconceptions and Challenges in Finding Velocity without Time

Suppose a stationary pull ball having a mass of 8kg is hit by another ball. After the collision, the ball is in motion at 5m/s. Determine the pool ball’s momentum after the collision.

How to Find Momentum after Collision Formula?

A football kicked the football having a mass of 5kg on the frictionless ground surface with a force of 30N over 5 sec. What is the velocity and momentum of football after kicking?

How to Find Total Momentum of Two Objects after Collision?

Suppose two marble pebbles having masses 10kg and 5kg moving at 8m/sec and 12 m/sec respectively; collide with each other. After the collision, both pebbles move away from each other with the same masses. If one pebble moves away with a velocity of 10m/sec, what is the second pebble’s velocity?

How to Find Momentum after Elastic Collision?

When a 10kg ball moving at 2m/s elastically collides with another ball having mass 2kg oppositely moving at 4m/s. Calculate the final velocities of both balls after the elastic collision.

How to Find Momentum after Inelastic Collision?

Quick Facts

What is momentum and why is it important in collisions?

What is the law of conservation of momentum?

How do you calculate the momentum of an object?

What are elastic and inelastic collisions?

What is the impulse-momentum theorem?

What happens to the momentum of two objects in a collision?

What is Newton’s third law and how does it relate to momentum?

How do you find the momentum after a collision?

What happens to the kinetic energy in a collision?

Is momentum conserved in all types of collisions?

How to Find the Slope of a Graph

Identifying the Rise and Run on a Graph

Calculating the Slope of a Straight Line Graph

Worked Out Examples on Finding the Slope of a Straight Line Graph

Finding the Slope of a Curve

Understanding the Concept of Slope for Curved Lines

Techniques to Calculate the Slope of a Curve

Worked Out Examples on Finding the Slope of a Curve

Special Cases in Finding the Slope of a Graph

Determining the Slope of a Horizontal Line

Problem 2) Calculate the initial velocity of the stone, which is falling from the height of 3m, and its acceleration is 2 m/s², and hence find the time taken by the stone to reach the ground.

Problem 5) A body of mass 4 kg is dropped at the height of 11 meters above the ground by making an angle of 20°. Calculate the velocity of the body. (Take acceleration due to gravity as 10 m/s²)

How to find velocity with acceleration and distance is given, if a motor vehicle is moving with a constant acceleration of 12 m/s² and covers a distance of 87 m, and hence find the time taken by the vehicle to cover the same distance.

In a race, the racer rides the bike with an initial velocity of 9 m/s. After time t, the velocity changes, and the acceleration is 3 m/s². The racer covers a distance of 10 m. calculate the final velocity of the bike to reach the given distance and hence find the average velocity of the bike.

An athlete runs with an initial velocity of 10 m/s. He covers 10 m with a constant acceleration of 4 m/s². Find the initial velocity.

Calculate the average velocity of particle moving with acceleration of 12 m/s² and the distance travelled by the particle is 26 meters.

A car travels a distance of 56 meters in 4 seconds. The acceleration of the car with the given time is 2 m/s². Calculate the initial velocity of the car.