In this article, we are going to discuss the relationship between frequency and energy, along with it we will solve some problems related to the topic with examples.
The frequency of the particle is relative to its energy. If the particle possesses a higher amount of energy, then, the frequency of the particle will be lofting, and hence the speed will be more.
Relationship between Frequency and Energy of Wave
The energy of a wave is characterized by the frequency of the occurrence of particles in a wave. The energy of any body is related to its frequency by the equation
E=hnu
Where h is a Planck’s constant h=6.626 * 10-34 J.s
nu is a frequency of the wave
The energy and the frequency are directly related to each other. If the energy possessed by the particle oscillating in a wave is more, then the frequency of the particle will be more.
It is also evident that a particle having greater energy will travel at high speed thus the wavelength of the propagating wave is less.
Problem 1: Find the energy of the particle having a frequency of 66PHz.
Given: h=6.626*10-34J.s
nu =66PHz= 66*1015 Hz
We have,
E=hnu
= 6.626 *10-34*66*1015
= 437.3*10-19Joules
The energy of the particle of frequency 66PHz is 437.3 *10-19Joules.
Read more on Energy And Wavelength Relationship: Problems, Example And Detailed Facts.
Graph of Energy and Frequency of Wave
The particle will travel at high speed if the amount of kinetic energy acquired by the particle is more. The speed of the particle is directly proportional to its wavelength. If the length of the wave of the particle is more, then the frequency of its occurrence will be lessened. The wavelength is inversely related to the energy of the particle.
The following is a graph of the energy v/s frequency of the waves.
The energy of the wave is directly related to the frequency. As the frequency of the wave increases, the energy will simultaneously increase, hence we have a linear slope of the graph.
Read more on What Is Constant In Velocity Time Graph: Detailed Facts.
Relationship between Frequency and Energy of Radiation
The frequency of the wave radiated from the object is more, when the radiations received by the surface of the object are high. The frequency of the wave is reduced at cooler temperatures as the wavelength of the radiated wave increases. At cooler temperatures, the emission of radiations is less, and radiations are emitted at the greater wavelengths.
Based on the wavelength and the frequencies of the wave, the waves are classified as follows:-
| Name | Radio Waves | Microwaves | Infrared | Visible | Ultra Violet | X-rays | Gamma rays |
| Wavelength | >1m | 1mm-1m | 700nm-1mm | 400nm-700nm | 10nm-380nm | 0.01nm-10nm | <0.01nm |
| Frequency | <300MHz | 300MHz-300GHz | 300GHz-430THz | 430THz-750THz | 750THz-30PHz | 30PHz-30EHz | >30Ehz |
From the above table, it is clearly indicating that as the wavelength of the radiations decreases the frequency of the wave increases. As the frequency of the waves increases, it implies that the energy of the waves also increases because the energy is linearly proportional to the frequency of the radiations.
The emissivity of the radiations is dependent on the dimensions of the object, the composition, and the color. The power of the emitted radiation is directly dependent upon the fourth power of the temperature the surface of the system is subjected to. The energy of the emitted radiations is given by the equation
U=ɛΣT4A
Where U is a radiated energy
ɛ is the emissivity of radiation from the object
Σ is the Stefan-Boltzmann constant and is equal to Σ=5.67*10-8W/m2K4
T is an absolute temperature
A is the area of the object
The black-colored objects are said to have an emissivity 1 because no radiations received by the black body are emitted by the object. All the radiations are completely absorbed by the black body. Whereas the white-colored object has the emissivity 0, as all the radiations that fall on the white objects are reflected back hence no radiations are absorbed by the objects.
As the temperature of the system increases, the frequency of the radiations is also increased parallelly.
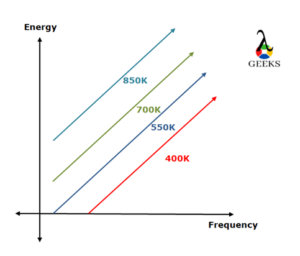
The above graph shows that as the temperature of the system increases, the energy of the emitted radiations increases with temperature. At low temperatures, the energy associated with the emitted radiations from the surface will be less; hence the radiations of higher wavelengths are emitted. Due to this, the frequency of the waves is decreased.
But, during the higher temperatures of the surrounding, the system will receive more amount of energy from the incident photons, hence the waves of fewer wavelengths will be given out, thus the frequency of the waves will increase. Well, the frequency linearly increases with increasing energy.
Read more on Radiation.
Problem 2: An object having a surface area of 28 sq.m is subjected to the temperature of 1120 Kelvin. The emissivity of the surface is 0.3. Calculate the rate of energy radiated from the object.
Given: ɛ =0.3
Σ=5.67*10-8W/m2K4
T=1120 K
A= 28 sq.m
The energy radiated by the box is
U=ɛΣT4A
=0.3*5.67*10-8*11204*28
= 2.67*104 Watts
= 26.7 KW
The power of the emitted radiations is 26.7KW.
Read more on Radiation Heat Transfer Examples:Critical Facts.
Relationship between Frequency and Energy of the Photon
The photon is a quantum particle of light that has zero rest mass. The energy of the photon in the electromagnetic radiation is directly proportional to the frequency of the photon and is given by the relation,
E=hnu
Where ‘h’ is a Planck’s constant h=6.626 * 10-34 J.s
nu is a frequency of the photon
The frequency of the photon is correlated to the speed and wavelength of the electromagnetic wave.
nu =v/λ
Since a photon is massless, the velocity of the photon is equal to the speed of light. Hence, the frequency of the photon is,
nu =c/λ
Therefore, the energy of the photon is related to the wavelength by the equation,
E=hc/λ
h=6.626 * 10-34 J.s
c is a velocity of light c=3*108m/s and
λ is a wavelength of the photon
If we know the wavelength of the particular light, then we can calculate the frequency and thereof the energy of the photons emitted by the source of light.
Problem 3: The wavelength of the sodium light beam is 588 nm. Calculate the frequency of the photon emitted from the sodium beam. Also, calculate the energy of the emitted photons.
Given: λ=588 nm
h=6.626 *10-34J.s
c=3 *108m/s
The frequency of the emitted photons is
nu =c/λ
=3 *108/ 588 *10-9
=176.4 THz
The frequency of the photon is 176.4 THz.
Now, the energy of the photon is
E=hnu
= 6.626 *10-34*1.764 *1014
= 11.67 *10-20 Joules
The energy of the photons is 11.67 * 10-20 Joules
Read more on What is Negative Frequency: Exhaustive Insights.
Relation between the Kinetic Energy and the Frequency
The kinetic energy of the particle having a mass ‘m’ and travelling with velocity ‘v’ is given by the formula
K.E=1/2 mv2
The velocity of the particle is directly related to the wavelength and the frequency of the wave of the particle. The frequency of the particle is given by the relation
f=v/λ
Where f is a frequency of the particle
V is a velocity and
λ is a wavelength of the particle
Hence,v=fλ
Using this in the above equation,
E=1/2 mf2λ2
2E = mf2λ2
2E/m = f2λ2
f2=2E/mλ2
f=√(2E/mλ2)
f=1/λ √(2E/mλ)
The above equation gives the relation between the energy and the frequency of the particle.
Read more on Why the coefficient of static friction is always greater than kinetic friction.
Example: Calculate the frequency of the electron possessing energy of 0.511 MeV. The transiting electrons are traveling with the wavelength of 530 nm.
Given: E = 0.511 MeV
E=0.511*106*1.6*10-19=0.817*10-13Joules
λ =530nm
m = 9.1 × 10-31 kg
We have,
f=1/λ √2ME
=1/(530 * 10-9) √2(0.18*1018)
=0.42*109/530*10-9
=0.79*1015
=0.79 PHz
The frequency of the electron is 0.79 PHz.
Frequently Asked Questions
What is the frequency of the photon having the energy of 16 × 10-10 Joules?
Given: E = 16 × 10-10 Joules
h=6.626 * 10-34.Js
We have,
E=hnu
nu =E/h
=16*10-10/6.626 *10-34
=2.41*1024 Joules
The energy of the photon is 2.41*1024 Joules.
What is the wavelength of the particle of mass 1.67 × 10-27 kg traveling at the speed of 2.5 × 108 m/s?
Given: v = 2.5 × 108 m/s
h=6.626 *10-34J.s
c=3 *108m/s
The kinetic energy of the photon is
K.E=1/2 mv2
=1/2 * 1.67*10-27 ( 2.5*108 )2
= 5.22*10-11Joules
Using de Broglie’s equation,
λ=h/p
The momentum of the particle,
p=√2ME
Hence,
λ =h/ √2ME
=6.626 * 10-34/√(2*1.67* 10-27*5.22*10-11
=6.626* 10-34/√17.43*10-38
=1.58 * 10-15m
The wavelength of the particle moving with velocity 2.5 × 108 m/s is 1.58 × 10-15 m.
What is a speed of the particle having a wavelength 2.68 pm and energy of 0.45MeV?
Given: E=0.45MeV=0.45*106* 1.6*10-19=0.72*10-13Joules
h=6.626 *10-34 J.s
c=3 *108m/s
We have E=hnu
nu =E/h
=0.72*10-13/6.626 *10-34
=0.108*1021=108EHz
Now, frequency is related to the speed by the relation
nu =v/λ
v=nuλ
v=108* 1018*2.68*10-12
=2.89*108 m/s
The speed of the particle is 2.89*108m/s.
How does the frequency affect the energy of the particle?
The energy is directly related to the frequency of the particle.
As the frequency of the wave increases, the energy of the particle propagating in the wave also increases.
Does the speed of the wave vary with the energy?
The speed of the particle increases on gaining the higher energy.
The frequency of the particle depends upon the energy which is directly proportional to the speed of the particle.
How does the frequency affect the power of the radiations?
The power of the radiations depends upon the emissivity of the objects and the temperature at which they are exposed.
At higher frequencies, the power of radiations is the maximum and at lower frequencies of the radiating photons, the power of the radiations is the minimum.
Also Read:
- Gravitational energy examples
- Motion energy examples
- Example of mechanical to radiant energy
- Is kinetic energy conserved
- Is potential energy stored energy
- Is mechanical energy conserved
- Mechanical energy to radiant energy
- Types of kinetic energy
- Kinetic energy to mechanical energy
- Example of mechanical energy to chemical energy
Hi, I’m Akshita Mapari. I have done M.Sc. in Physics. I have worked on projects like Numerical modeling of winds and waves during cyclone, Physics of toys and mechanized thrill machines in amusement park based on Classical Mechanics. I have pursued a course on Arduino and have accomplished some mini projects on Arduino UNO. I always like to explore new zones in the field of science. I personally believe that learning is more enthusiastic when learnt with creativity. Apart from this, I like to read, travel, strumming on guitar, identifying rocks and strata, photography and playing chess.