Image Credit: Schwarzbeck Mess-Elektronik, Schwarzbeck BBHA 9120 D, CC BY-SA 3.0
Points for Discussion: Horn Antenna
- Introduction
- Use of horn antenna
- Elements of a horn antenna and Types of horn antenna
- Horn antenna design
- Directivity of horn antenna
- Horn antenna radiation pattern
- Horn antenna gain
- Horn antenna beamwidth
- Few mathematical problems related to Horn Antenna
Introduction
To define a horn antenna, we should know the proper definition of the antenna. According to IEEE standard definitions of antennas,
“An antenna is a means for radiating or receiving radio waves”.
Horn antenna is the most popular type of Aperture antenna. Aperture antennas are specially designed for microwave frequencies. These types of aperture antennas are widely used and most unadorned other than any kinds.
Though horn antenna usage was started back in the 1800s, the rapid application was created in the 1930s. These antennas had also undergone drastic modification during this time. Numerous thesis and research were done to describe the horn-antenna’s design, find out the radiation pattern of horn-antenna, and applications in different sectors. The applications in microwave and waveguide transmission domain made horns antenna famous. That is why horn- antennas are often interpreted as a microwave horn-antenna.
What is Transmission Line? How it is related to antenna? Know here!
Use of Horn Antenna
Horn-antennas have found impactful applications as feed elements for hefty radio astronomy, satellite tracking, communication dishes, and many other places. It is used as a feed for reflector and lenses and also used in phased arrays. These antennas are preferred over different types of aperture antennas, because of its fair and straightforward design, better gain, versatility, and overall performance.
Elements of a horn antenna
Horn antenna is a resonating pipe of various designs which can be shaped for making a larger opening. The overall performance of the antenna is affected by the direction, taper’s amount, directivity.
Types of horn antenna
Horn-antennas have different forms for operations. They are –
· Sectoral Horn Antenna
- E-Plane
- H-Plane
· Pyramidal Horn Antenna

· Conical Horn Antenna

· Corrugated horn antenna

· Diagonal horn antenna

· Ridged horn antenna

· Dual-mode conical horn antenna
· Septum horn antenna
· Aperture-limited horn antenna
Horn antenna design (Pyramidal Horn Antenna)
Pyramidal horn-antenna is the most used and popular types of the horn-antenna. It is known as a standard gain horn (that is why we choose pyramidal horn for describing). The pyramidal horn’s radiation pattern is the combination of E- and H- sectoral horn-antennas. Let us discuss the design of a pyramidal horn-antenna.
Design Procedure
- The designer/ engineer should know the gain (G0). Also the measurements of ‘a’, ‘b’, of the quadrilateral waveguide (used as feed) should be known.
- The designing aims to derive dimensions such as – a1, b1, ρe, ρh, Pe, Ph. The calculation should lead the designer to the optimum gain of the horn- antenna.
- The selection of a1 and b1 should also be in a guided way so that they will help to find the optimum gain, and we can derive the design equations.
- The efficiency of a horn- antenna including the apertures is about 50%. Now, we know that –
a1 ≈ √ (3λρ2)
b1 ≈ √ (2λρ1)
The directivity is given as – D0
D0 = Aem [ 4π / λ2]
Aem is the maximum effective area and has a relationship with the physical area (abbreviated as Ap).
Aem = εap Ap
εap is the aperture efficiency, 0 ≤ εap ≤ 1
Gain = G0
G0 = (1/2) * (4π / λ2) * (a1 b1)
Or, G0 = (2π / λ2) * √ (3λρ2) * √ (2λρ1)
Or, G0 ≈ (2π / λ2) * √ (3λρh * 2λρe) — (1)
As we assume ρ2 ≈ ρh and ρ1 ≈ ρe for long horn-antennas.
Now, to realize the physical horn- antenna, Pe and Ph must be equal.
We know that,
Pe = (b1 – b) [ (ρe / b1)2 – ¼]1/2
Ph = (a1 – a) [ (ρh / a1)2 – ¼]1/2
Now, we can rewrite the equation (1) as below.
[√ (2χ) – b/ λ]2 (2χ -1) = [{(G0 /2π√χ) * √ (3/2π)} – (a/ λ)]2 * [(G02 / 6π3χ) – 1] — (2)
Where,
ρe / λ = χ and,
ρh / λ = G02 / 8π3χ
Equation (2) is known as the horn- antenna design equation.
- At first, we have to calculate the value of χ, which will gratify the value of gain. An iterative approach with a trial value is considered to find out the value χ.
χ (trail) = χ1 = G0 /2π√2π
- Once the correct value is calculated, the value of ρe and ρh are calculated.
- The a1 and b1 related to the designs are calculated after that.
a1 = √ (3λρ2) ≈ √ (3λρh) = (G0 /2π) * √ (3λ/2πχ)
b1 = √ (2λρ1) ≈ √ (2λρe) = √ (2λχ)
- The values of pe and ph are calculated at last.
Directivity of Horn Antenna
Before we step into finding out the directivity of a horn-antenna, let us know the directivity of an antenna? An antenna’s directivity is defined as the ratio of radiation intensity of an antenna in a particular direction to the averaged radiation intensity over all the directions. Directivity is considered as a parameter for calculating the figure of merit of the antenna.
The following mathematical expression describes the directivity.
D = U / U0 = 4πU / Prad
When the direction is not given, the default direction is the direction of maximum radiation intensity.
Dmax = D0 = Umax / U0 = 4πUmax / Prad
Here, ‘D’ is the directivity, and it has no direction as it is a ratio. U is the radiation intensity. Umax is the maximum radiation intensity. U0 is the radiation intensity of the isotropic source. Prad is the total radiated power. Its unit is Watt (W).
As earlier said, the horn-antenna is of three types. All the classes have different directivity. Let us discuss all of them.
E-Plane Sectoral Horn
The following expression gives the directivity of the E-Plane horn-antenna.
DE = 4πUmax /Prad = (64aρ1 * | F(t) | 2)/πλ b1
Where, | F(t) | = [C2b1 / √ (2λρ1) + S2b1 / √ (2λρ1)]
H-Plane Sectoral Horn
The following expression gives the directivity of the H-plane sectoral horn-antenna.
DH = 4πUmax /Prad = [4πbρ2 /a1 λ]* {[ C(u) – C(v)]2 + [S(u) – S(v)]2}
Where,
u = (1/√2) * [{√ (λρ2)/a1 + a1/ √ (λρ2)}]
v = (1/√2) * [{√ (λρ2)/a1 – a1/ √ (λρ2)}]
Pyramidal Horn Antenna
The directivity of pyramidal horn- antenna depends on both the directivity of E & H plane sectoral horn. The equation is given below.
DP = 4πUmax /Prad = [8πρ1ρ2 /a1b1] * {[ C(u) – C(v)]2 + [S(u) – S(v)]2} * {[C2b1 / √ (2λρ1) + S2b1 / √ (2λρ1)]}
It can be written as –
DP = [π λ2 / 32ab] * DEDH
Horn Antenna Radiation Pattern
Radiation Pattern is the angular dependence of the strength of the radio waves from any electromagnetic source. The below image shows the radiation pattern of a pyramidal horn-antenna.
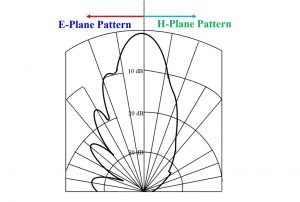
Image depicting Horn antenna radiation pattern
Horn Antenna Gain
An antenna’s gain would refer to as the ratio of the intensity in a particular direction to the radiation intensity if the antenna were radiated isotopically. It is an essential parameter for measuring an antenna’s performance and has a close relationship with the antenna’s directivity. The gain of a horn- antenna lies around 25 dBi and the range is typically 10 – 20 dBi.
Horn antenna beamwidth
Antenna bandwidth is the angular distance between two matching points on the reverse side of the outline supreme. The horn-antenna beamwidth gets decreased if the frequency of the process gets increased.
The bandwidth of a practical horn-antenna stays in a range of 10:1 to 20:1.
Few mathematical problems related to Horn Antenna
1. Find the directivity of the E-plane sectoral horn-antenna. The details for the antenna are given below. a = 0.5λ, b = 0.25λ, b1 = 6λ, ρ1 = 6λ
Solution:
b1 / √ (2λρ1) = 6λ / √ (2λ*6λ) = 6 / √12 = 1.73
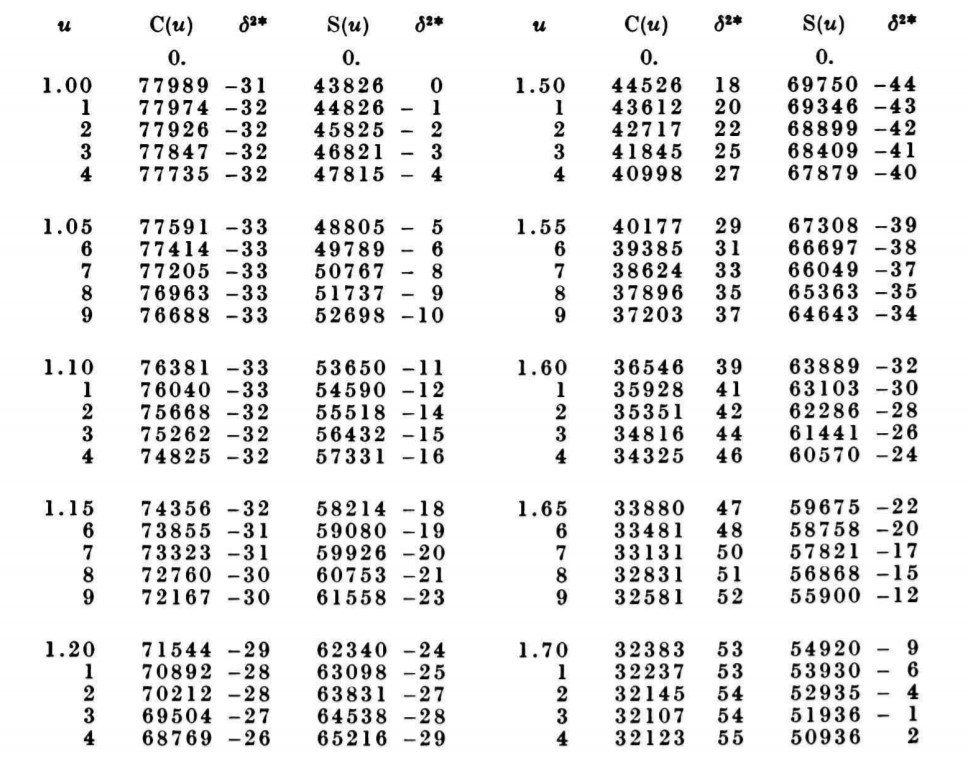
A part of Fresnel Integral Chart; Image Credit – A. VAN WIJNGAARDEN and W. L. SCHEEN
Now, [C (1.73)]2 = (0.32)2 = 0.1024 [from the chart of Fresnel integrals]
And, [S (1.73)]2 = (0.54)2 = 0.2916 [from the chart of Fresnel integrals]
We know that, DE = 4πUmax /Prad = (64aρ1 * | F(t) | 2)/πλb1
Where, | F(t) | = [C2b1 / √ (2λρ1) + S2b1 / √ (2λρ1)]
DE = [{64 (0.5) * 6 * (0.1024 + 0.2916)} / 6π]
Or, DE = 4.01 dB.
So, the directivity of the given E-Plane Sectoral Horn-Antenna is 4.01 dB.
2. Find the directivity of the H-plane sectoral horn-antenna. The details of the antenna are given below. a = 0.5λ, b = 0.25λ, a1 = 6λ, ρ2 = 6λ
Solution:
We know that,
u = (1/√2) * [{√ (λρ2)/a1 + a1/ √ (λρ2)}]
v = (1/√2) * [{√ (λρ2)/a1 – a1/ √ (λρ2)}]
Now, u = (1/√2) * [{√ (6)/6 + 6/ √ (6)}] = 2.02
And, v = (1/√2) * [{√ (6)/6 – 6/ √ (6)}] = – 1.44
Using Fresnel integrals,
C (u) = C (2.02) = 0.48825
C (v) = C (-1.44) = -C (1.44) = – 0.54310
S (u) = S (2.02) = 0.3434
S (v) = S (-1.44) = -S (1.44) = – 0.71353
We know that directivity of H-plane sectoral horn- antenna is
DH = 4πUmax /Prad = [4πbρ2 /a1 λ]* {[C(u) – C(v)]2 + [S(u) – S(v)]2}
Or, DH = [4π (0.25)6/6] * [ (0.488 + 0.543)2 + (0.343 + 0.713)2]
Or, DH = (3.141) * (1.0629 + 1.1151)
Or, DH = 6.84 dB
So, the directivity of the given H-plane Sectoral Horn-Antenna is 6.84 dB.
3. Designing details of a pyramidal horn-antenna is given below. ρ2 = 6λ = ρ1 = 6λ; a = 0.5λ, b = 0.25λ; a1 = 6λ = b1 = 6λ; Check if a practical horn-antenna can be designed with those details. Also, find out the directivity of the pyramidal horn- antenna.
Solution:
Now, ρe = λ √ ([62+ (6 / 2)2] = 6.708λ
And, ρh = λ √ ([62+ (6 / 2)2] = 6.708λ
We know that,
Pe = (b1 – b) [ (ρe / b1)2 – ¼]1/2
Ph = (a1 – a) [ (ρh / a1)2 – ¼]1/2
Now, Pe = (6λ– 0.25λ) [ (6.708 / 6)2 – ¼]1/2 = 5.74λ
And, Ph = (6λ– 0.5λ) [ (6.708 / 6)2 – ¼]1/2 = 5.12λ
As we can see, Pe is not equal to Ph, so the design is not possible to implement.
We know that the directivity of a pyramidal horn-antenna is
DP = [π λ2 / 32ab] * DEDH
Now, DP = [π / 32 * (0.5) * (0.25)] * 6.84 * 4.01]
[The value of DEDH is has been calculated previously]
Or, DP = 21.54
Converting it to the dB value, DP = 10log21.54 = 13.33 dB
So, the directivity of the given Pyramidal Horn-antenna is 13.33 dB.

Hi, I am Sudipta Roy. I have done B. Tech in Electronics. I am an electronics enthusiast and am currently devoted to the field of Electronics and Communications. I have a keen interest in exploring modern technologies such as AI & Machine Learning. My writings are devoted to providing accurate and updated data to all learners. Helping someone in gaining knowledge gives me immense pleasure.
Let’s connect through LinkedIn –