Mechanical Engineering

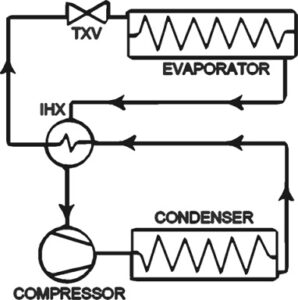
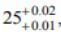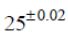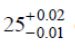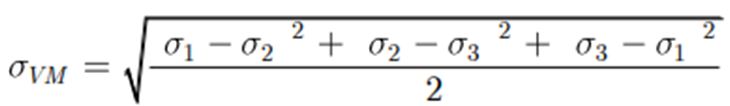Specific Enthalpy vs Enthalpy

Enthalpy is a fundamental concept in thermodynamics that measures the total heat content of a system. It is often used to describe the energy changes that occur during chemical reactions or phase transitions. However, there is another term closely related to enthalpy known as specific enthalpy. While both terms are used to quantify energy changes, they have distinct differences in their definitions and applications. In this article, we will explore the differences between specific enthalpy and enthalpy, and understand how they are used in various fields of science and engineering. So, let’s dive in and unravel the mysteries behind these two important concepts in thermodynamics.

Key Takeaways

• Enthalpy is a thermodynamic property that represents the total heat content of a system, while specific enthalpy is the enthalpy per unit mass of a substance.
• Specific enthalpy is useful in engineering applications as it allows for more accurate calculations and comparisons between different substances.
• Enthalpy is typically measured in units of energy, such as joules or calories, while specific enthalpy is measured in units of energy per unit mass, such as joules per kilogram.
• The specific enthalpy of a substance can be calculated by dividing the enthalpy by the mass of the substance.
• Both enthalpy and specific enthalpy are important concepts in thermodynamics and are used to analyze and design various processes and systems.

Enthalpy vs Specific Enthalpy

Enthalpy: Definition and Components (Internal Energy and Pressure-Volume Work)

Enthalpy is a fundamental concept in thermodynamics that helps us understand the energy content of a system. It is denoted by the symbol “H” and is defined as the sum of the internal energy (U) and the product of pressure (P) and volume (V) of the system. In other words, enthalpy accounts for both the heat energy and the work done by the system.

The internal energy represents the total energy stored within the system, including the kinetic and potential energies of its particles. On the other hand, the pressure-volume work accounts for the energy transferred to or from the system due to changes in its volume under constant pressure.

Specific Enthalpy: Definition as Enthalpy per Unit Mass

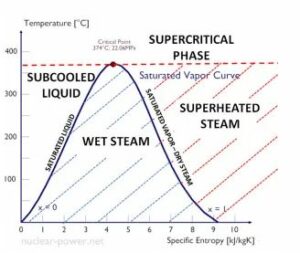
Specific enthalpy, denoted as “h,” is the enthalpy per unit mass of a substance. It is obtained by dividing the enthalpy (H) of the system by its mass (m). Specific enthalpy allows us to analyze the energy content of a substance on a per-unit-mass basis, which is particularly useful in engineering and thermodynamic calculations.

By expressing enthalpy in terms of mass, specific enthalpy enables us to compare the energy content of different substances or different amounts of the same substance.

Comparison between Enthalpy and Specific Enthalpy

The main difference between enthalpy and specific enthalpy lies in their units and the way they are used. Enthalpy is an extensive property, meaning it depends on the size or amount of the system. On the other hand, specific enthalpy is an intensive property, which remains constant regardless of the system size.

Enthalpy allows us to analyze the total energy content of a system, taking into account both the internal energy and the work done. It is commonly used in thermodynamic calculations, such as determining the heat transfer in chemical reactions or phase changes.

Specific enthalpy, on the other hand, provides a more detailed analysis by considering the energy content on a per-unit-mass basis. It is particularly useful in engineering applications, such as calculating the energy required for heating or cooling a specific mass of a substance.

Units of Measurement for Enthalpy and Specific Enthalpy

Enthalpy is typically measured in units of energy, such as joules (J) or calories (cal). The SI unit for enthalpy is joule, while the calorie is commonly used in the field of chemistry.

Specific enthalpy is expressed in the same units as enthalpy but divided by mass. Therefore, the units for specific enthalpy are joules per kilogram (J/kg) or calories per gram (cal/g).

To summarize, enthalpy and specific enthalpy are both important concepts in thermodynamics. Enthalpy provides a comprehensive analysis of the energy content of a system, while specific enthalpy allows for a more detailed examination on a per-unit-mass basis. Understanding these concepts is crucial for engineers, scientists, and anyone working with energy systems.

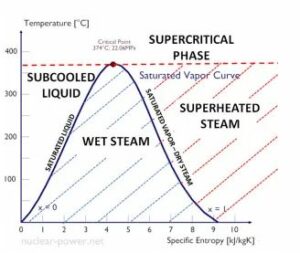
Specific Enthalpy of Steam Water System

The specific enthalpy of a steam water system is a crucial thermodynamic property that helps us understand the energy content of the system. It is defined as the amount of heat energy per unit mass of a substance, and it plays a significant role in various engineering applications, particularly in the field of thermodynamics.

Specific Enthalpy Values for Vaporization and Saturation of Water

When water undergoes a phase change from a liquid to a vapor state, it requires a certain amount of energy. This energy is known as the specific enthalpy of vaporization. It represents the heat energy needed to convert one unit mass of liquid water into vapor at a given temperature and pressure.

Similarly, the specific enthalpy of saturation refers to the energy content of water when it exists in a saturated state. In this state, water is at the boiling point corresponding to a specific pressure. The specific enthalpy of saturation is the sum of the specific enthalpy of liquid water and the specific enthalpy of vaporization.

Calculation of Specific Enthalpy for Saturated Steam at Atmospheric Pressure

To calculate the specific enthalpy for saturated steam at atmospheric pressure, we need to consider the specific enthalpy of liquid water and the specific enthalpy of vaporization. The specific enthalpy of liquid water can be determined using tables or equations based on temperature. The specific enthalpy of vaporization can also be obtained from tables or correlations.

By adding the specific enthalpy of liquid water and the specific enthalpy of vaporization, we can determine the specific enthalpy of saturated steam at atmospheric pressure. This value represents the energy content of steam in its saturated state.

Increase in Specific Enthalpy with System Pressure

As the pressure of a steam water system increases, the specific enthalpy also increases. This is because higher pressures require more energy to convert water into steam. The specific enthalpy of steam at a given pressure is higher than that at atmospheric pressure due to the additional energy required for vaporization.

The increase in specific enthalpy with system pressure is an important consideration in various industrial processes, such as power generation and steam-driven machinery. Understanding the relationship between pressure and specific enthalpy allows engineers to design efficient systems and optimize energy usage.

Calculation of Specific Enthalpy for Superheated Steam

Superheated steam refers to steam that has been heated beyond its saturation point. To calculate the specific enthalpy for superheated steam, we need to consider the specific enthalpy of saturated steam and the specific enthalpy of superheating.

The specific enthalpy of saturated steam can be determined as mentioned earlier. The specific enthalpy of superheating represents the additional energy required to heat the steam beyond its saturation point. This value can be obtained from tables or correlations based on the temperature and pressure of the superheated steam.

By adding the specific enthalpy of saturated steam and the specific enthalpy of superheating, we can determine the specific enthalpy of superheated steam. This value represents the total energy content of steam in its superheated state.

Molar Enthalpy vs Specific Enthalpy

Definition of Molar Enthalpy and Specific Enthalpy

Enthalpy is a fundamental concept in thermodynamics that measures the total energy of a system. It is denoted by the symbol “H” and is often used to describe heat transfer and energy changes in chemical reactions. Molar enthalpy and specific enthalpy are two related but distinct concepts that are commonly used in different contexts.

Molar enthalpy, also known as molar heat capacity, is the amount of heat required to raise the temperature of one mole of a substance by one degree Celsius. It is represented by the symbol “Cp” and has units of joules per mole per degree Celsius (J/mol·°C). Molar enthalpy takes into account the mass of the substance and is used to calculate the enthalpy change in reactions.

On the other hand, specific enthalpy, also known as specific heat capacity, is the amount of heat required to raise the temperature of a unit mass of a substance by one degree Celsius. It is represented by the symbol “cp” and has units of joules per kilogram per degree Celsius (J/kg·°C). Specific enthalpy is used for heat balance calculations in engineering and is independent of the mass of the substance.

Differences between Molar Enthalpy and Specific Enthalpy

The main difference between molar enthalpy and specific enthalpy lies in the units of measurement and the quantity being considered. Molar enthalpy is expressed in terms of moles of a substance, while specific enthalpy is expressed in terms of kilograms of a substance.

Molar enthalpy takes into account the mass of the substance and is used to calculate the enthalpy change in reactions. It is particularly useful in chemical reactions where the quantities involved are often measured in moles. Specific enthalpy, on the other hand, is used for heat balance calculations in engineering, where the focus is on the energy required to heat or cool a given mass of a substance.

Molar Enthalpy used for calculating enthalpy change in reactions

Molar enthalpy is commonly used in chemical reactions to calculate the enthalpy change, also known as the heat of reaction. The enthalpy change is the difference in enthalpy between the products and the reactants in a chemical reaction. By knowing the molar enthalpies of the reactants and products, it is possible to calculate the enthalpy change using the principle of conservation of energy.

For example, in the combustion of methane (CH4), the molar enthalpy of methane is -890.3 kJ/mol, and the molar enthalpy of carbon dioxide (CO2) is -393.5 kJ/mol. By subtracting the molar enthalpy of the reactants from the molar enthalpy of the products, the enthalpy change of the reaction can be determined.

Specific Enthalpy used for heat balance calculations in engineering

Specific enthalpy is widely used in engineering for heat balance calculations. Heat balance calculations involve determining the amount of heat energy required to heat or cool a given mass of a substance. Specific enthalpy allows engineers to calculate the energy requirements for various processes, such as heating water or cooling air.

For example, in HVAC (Heating, Ventilation, and Air Conditioning) systems, specific enthalpy is used to calculate the energy required to heat or cool air as it flows through the system. By knowing the specific enthalpy of the incoming and outgoing air, engineers can determine the amount of energy needed to achieve the desired temperature change.

Units of measurement for Molar Enthalpy and Specific Enthalpy

Molar enthalpy is measured in joules per mole per degree Celsius (J/mol·°C), while specific enthalpy is measured in joules per kilogram per degree Celsius (J/kg·°C). These units reflect the different quantities being considered – moles for molar enthalpy and kilograms for specific enthalpy.

Calculation of total enthalpy change using Molar Enthalpy and Specific Enthalpy

To calculate the total enthalpy change in a system, both molar enthalpy and specific enthalpy can be used. The molar enthalpy is used to determine the enthalpy change at the molecular level, while the specific enthalpy is used to determine the enthalpy change at the mass level.

The total enthalpy change can be calculated by multiplying the molar enthalpy by the number of moles involved in the reaction and adding it to the product of the specific enthalpy and the mass of the substance. This allows for a comprehensive understanding of the energy changes occurring in a system.

Different Types of Enthalpy Change

Enthalpy change refers to the amount of heat energy transferred during a chemical reaction or physical process. There are various types of enthalpy changes that occur in different scenarios. Let’s explore some of the most common types of enthalpy changes.

Explanation of Various Types of Enthalpy Changes

1. Enthalpy of Reaction: The enthalpy change associated with a chemical reaction is known as the enthalpy of reaction. It represents the difference in enthalpy between the products and the reactants. This value can be positive or negative, depending on whether the reaction is exothermic (releases heat) or endothermic (absorbs heat).

2. Enthalpy of Combustion: The enthalpy change that occurs during the combustion of a substance is called the enthalpy of combustion. It measures the heat energy released when a substance reacts with oxygen to form carbon dioxide and water.

3. Enthalpy of Formation: The enthalpy change when one mole of a compound is formed from its constituent elements in their standard states is known as the enthalpy of formation. It provides information about the stability and energy content of the compound.

4. Enthalpy of Neutralization: The enthalpy change that occurs when an acid reacts with a base to form a salt and water is called the enthalpy of neutralization. It represents the heat energy released or absorbed during the neutralization process.

5. Enthalpy of Solution: The enthalpy change associated with the dissolution of a solute in a solvent is known as the enthalpy of solution. It measures the heat energy released or absorbed when a solute dissolves to form a solution.

6. Enthalpy of Fusion: The enthalpy change when a substance changes from a solid to a liquid state at its melting point is called the enthalpy of fusion. It represents the heat energy required to overcome the intermolecular forces holding the solid together.

7. Enthalpy of Sublimation: The enthalpy change when a substance changes directly from a solid to a gaseous state without passing through the liquid state is known as the enthalpy of sublimation. It measures the heat energy required to overcome the forces holding the solid together and convert it into a gas.

8. Enthalpy of Vaporization: The enthalpy change when a substance changes from a liquid to a gaseous state at its boiling point is called the enthalpy of vaporization. It represents the heat energy required to overcome the intermolecular forces holding the liquid together.

9. Enthalpy of Mixing: The enthalpy change that occurs when two or more substances are mixed together is known as the enthalpy of mixing. It measures the heat energy released or absorbed during the mixing process.

By understanding these different types of enthalpy changes, we can gain insights into the energy transformations that occur during chemical reactions and physical processes. These values play a crucial role in various scientific and engineering applications, such as designing efficient energy systems and understanding the thermodynamics of chemical reactions.

Favorable Enthalpy

Enthalpy is a fundamental concept in thermodynamics that helps us understand the energy changes that occur during chemical reactions. It plays a crucial role in determining whether a reaction is favorable or not. In this section, we will explore the relationship between enthalpy change and reaction favorability, as well as introduce the concept of Gibbs free energy.

Favorability of a reaction based on enthalpy change

The enthalpy change of a reaction, often denoted as ΔH, is a measure of the heat energy absorbed or released during a chemical reaction. It represents the difference in enthalpy between the products and the reactants. By analyzing the sign and magnitude of ΔH, we can determine whether a reaction is exothermic or endothermic.

An exothermic reaction releases heat energy to the surroundings, resulting in a negative ΔH value. On the other hand, an endothermic reaction absorbs heat energy from the surroundings, leading to a positive ΔH value. The magnitude of ΔH indicates the amount of heat energy involved in the reaction.

Relationship between enthalpy change and entropy change

Entropy, denoted as ΔS, is a measure of the disorder or randomness in a system. It accounts for the number of ways in which the particles of a system can be arranged. A positive ΔS value indicates an increase in disorder, while a negative ΔS value suggests a decrease in disorder.

The relationship between enthalpy change (ΔH) and entropy change (ΔS) is described by the equation:

ΔG = ΔH – TΔS

where ΔG is the Gibbs free energy change and T is the temperature in Kelvin. The Gibbs free energy change determines the spontaneity of a reaction. If ΔG is negative, the reaction is spontaneous and favorable. If ΔG is positive, the reaction is non-spontaneous and unfavorable. If ΔG is zero, the reaction is at equilibrium.

Gibbs free energy (ΔG) is a thermodynamic potential that combines the effects of enthalpy change (ΔH) and entropy change (ΔS) to determine the spontaneity of a reaction. It provides a more comprehensive understanding of reaction favorability compared to enthalpy alone.

The equation ΔG = ΔH – TΔS tells us that for a reaction to be favorable, the enthalpy change must be negative (exothermic) and the entropy change must be positive (increase in disorder). However, the temperature also plays a crucial role. At low temperatures, a negative enthalpy change dominates, making the reaction favorable. At high temperatures, a positive entropy change dominates, making the reaction favorable.

Frequently Asked Questions

1. Why are enthalpy values different?

Enthalpy values can vary depending on the specific process or reaction being considered. Factors such as temperature, pressure, and the presence of other substances can influence the enthalpy of a system, leading to differences in the measured values.

2. Is enthalpy the same as specific heat?

No, enthalpy and specific heat are different properties. Enthalpy is a measure of the total energy of a system, including both its internal energy and the work done on or by the system. Specific heat, on the other hand, is a measure of the amount of heat required to raise the temperature of a unit mass of a substance by a certain amount.

3. What is the difference between specific heat capacity and enthalpy?

Specific heat capacity refers to the amount of heat required to raise the temperature of a unit mass of a substance by a certain amount. Enthalpy, on the other hand, is a measure of the total energy of a system, including both its internal energy and the work done on or by the system. While specific heat capacity is a property of a substance, enthalpy is a property of a system.

4. Why is the experimental enthalpy higher than the theoretical value?

There can be several reasons for the experimental enthalpy to be higher than the theoretical value. Experimental errors, incomplete reactions, side reactions, and impurities in the reactants can all contribute to the deviation between the experimental and theoretical enthalpy values.

5. What is the difference between standard enthalpy and enthalpy?

Standard enthalpy refers to the enthalpy change that occurs under standard conditions, which typically include a temperature of 25°C and a pressure of 1 bar. Enthalpy, on the other hand, is a more general term that refers to the total energy of a system, including both its internal energy and the work done on or by the system.

6. What is specific enthalpy?

Specific enthalpy is the enthalpy per unit mass of a substance. It is a measure of the total energy of a unit mass of a substance, including both its internal energy and the work done on or by the substance.

7. What is the difference between enthalpy change and standard enthalpy change?

Enthalpy change refers to the difference in enthalpy between the reactants and the products in a chemical reaction. It can be positive (endothermic) or negative (exothermic). Standard enthalpy change, on the other hand, refers to the enthalpy change that occurs under standard conditions, typically at a temperature of 25°C and a pressure of 1 bar.

8. What is the difference between specific enthalpy and enthalpy?

Specific enthalpy refers to the enthalpy per unit mass of a substance, while enthalpy is a more general term that refers to the total energy of a system. Specific enthalpy takes into account the mass of the substance, whereas enthalpy does not.

9. What is the difference between enthalpy of formation and enthalpy of reaction?

Enthalpy of formation refers to the enthalpy change that occurs when one mole of a compound is formed from its constituent elements in their standard states. Enthalpy of reaction, on the other hand, refers to the enthalpy change that occurs in a chemical reaction, regardless of the formation of new compounds.

10. What is the difference between enthalpy of mixing and enthalpy of solution?

Enthalpy of mixing refers to the enthalpy change that occurs when two or more substances are combined to form a mixture. Enthalpy of solution, on the other hand, refers to the enthalpy change that occurs when a solute is dissolved in a solvent to form a solution.

This article discusses about bending strength of steel. Bending strength is the ability of a material to resist or withstand the bending stress applied.

Strength is ability to withstand or resist a particular amount of stress. A material has a particular amount of strength, only that much stress it can withstand. Any amount of stress which exceeds the strength can lead to material failure. Simply put, the applied stress should be lesser than the strength of the material for minimizing failure.

What is bending strength?

Bending strength or flexural rigidity is the ability of a work piece to withstand bending stress. The flexural strength depends on the failure load, effective length of the work piece and the dimensions of the cross section of the beam.

Mathematically the bending strength is given as-

σ_b = M.y/I

where,

sigma is bending strength or maximum allowable bending stress that can be applied before fracture

M is the bending moment

I is the moment of inertia of the cross section of the work piece

What is bending stiffness?

Bending stiffness and bending strength are not same. As discussed above, bending strength is the ability of the work piece to withstand a given amount of bending stress.

On the other hand, bending stiffness tells the amount of deflection the work piece will undergo under a given amount of bending stress. The bending stiffness depends on moment of inertia of cross section the work piece and the modulus of rigidity of the material of work piece.

Mathematically, bending stiffness can be given as-

Bending stiffness = E x I

Where, E is the Young’s modulus or modulus of rigidity

I is the moment of inertia of the cross section of the work piece

Bending strength of stainless steel

The bending strength not only depends on the material but the dimensions of the work piece too. The table below shows the bending strength of a stainless steel bar.

Bending strength of steel pipe

Steel pipes are used at a large scale in industries. It is very important to know the physical properties of steel pipe and the behaviour of these pipes under different types of loads.

Bending strength of steel pipe can be found using the formula given below-

σ = 32MD/π(D⁴-d⁴)

where,

D is the outer diameter of pipe

d is the inner diameter of pipe

Pipe is simply a hollow cylinder.

Bending strength of steel plate

Let us assume a steel plate having a depth d and breadth b. The permissible load acting it is P.

The bending strength of this steel plate is given by following-

σ = 3M/bd²

Plate has a rectangular cross section where,

b is the breadth

d is the depth of rectangle

M is the bending moment

Bending strength of steel rod

Steel rods are widely used in construction industry for reinforcement purpose. They are used in aircrafts as well. To avoid construction failure, it is very important to know the mechanical properties of rods being used.

Let us consider a steel rod of diameter d. The bending strength can be given by the following formula-

σ = 32M/πd³

Bending strength of steel bar

Let us assume a circular steel bar of diameter d having permissible force value P. Then the bending strength formula for steel bar will be same as that of steel rod.

The bending strength of steel rod is discussed in above sections.

Bending strength of steel channel

Let us consider a “I” steel channel as shown in the figure below.

To find the moment of inertia of the entire cross section, we add the individual moment of inertia of the parts A, B and C.

The bending strength of this channel can be written from the basic formula. That is,

σ_b =M.y/I

Bending strength of steel square tube

Square tube is simply a hollow square cross section tube. These tubes are used in construction industry and interior designing. It is very important to know the bending strength of square tube before taking into use.

The section modulus of a square tube can be given by-

σ = bd³/3

Hence the bending strength becomes,

σ = 3M/ bd³

How to calculate bending strength of steel

Bending strength can be found using flexural test. Flexural tests can be performed with a single axial load, three point loading set up and four point loading set up.

Let us consider a three point set up. The given data for the set up is given below-

The work piece is a rectangular bar having breadth of 10cm and depth of 10 cm. The length of the bar is 1m and the load at failure is 10kN.

To find the bending strength of in a three point flexural test, following formula is used-

σ = 3FL/ 2bd²

Substituting all the values in above formula we have,

Bending strength= 15 MPa

How to calculate yield strength of steel

Yield strength of any material can be found using a tensile test on universal testing machine. The machine pulls the work piece from its ends and provides us with a stress strain graph from which we can easily make out the tensile strength of the material.

Let us consider the given data-

Load at failure- 5kN

Area of cross section- 1mm^2

The yield strength can be calculated using the formula-

S_yt = P/A

Substituting the values in above equation we get,

Yield strength= 500Mpa

The diagram obtained from this test is commonly called as stress strain diagram.

Stress strain diagram

The graph which shows relationship between stress and strain is called as stress strain diagram.

This graph gives information like yield point, proportional limit, fracture point and ultimate tensile strength of the specimen. This diagram makes it easy to measure the mechanical properties of the specimen.

In this article we will discuss about the “Low discharge superheat” and its related factors.

The Low discharge superheat is when the refrigerant liquid flooding to the compressor or in the screw compressor in the very low oil temperature. The insufficient amount of air flows through the evaporator coils causes low discharge superheat.

With a high ambient temperature the refrigerant liquid go back to the compressor which causes the leakage to the heat exchangers and liquid injection device if it is fitted. This condition also point to an Actuator or Check valve issue. A dirty air filter, evaporator coil or air flow causes discharge measure low. The heat which is carried by the coils is low which result in low discharge superheat.

Process:

The low discharge superheat can be obtaind by the following,

• At first we need to run the refrigeration system minimum for 10 min.
• When the system running for a while we have to attach the pipe clamp thermocouple in one side of the refrigerant line which actually separate the thermal expansion valve and the condenser discharge valve.
• Connect with the refrigerant manifold gauges with discharge service valve.
• Read refrigerant manifold gauge to check the discharge service valve.
• Check the thermocouple temperature using a digital thermometer.
• Measure the pressure chart and temperature for the refrigerant.
• Now need to turn over the condenser pressure reading to a condenser saturation temp.
• Pressure takes from the thermocouple and the temperature of the condenser saturation from it.

Formula:

The low discharge superheat is calculated in the way as any other discharge superheat calculated on a system, by measuring the low discharge superheat and have to subtract the suction superheat and then then leaves with a figure of how much low superheat the compressor has given through compression and mechanical/electrical inefficiencies.

Work:

Prevent damage the machine from worn rings, acid formation and oils breakdowns and make it run more effective.

Example:

Let, the Discharge Temperature = 152, Condensing Sat. Temp. = 91

Then the discharge superheat would be = 61

Exhaustive facts:

In the discharge superheat refrigerant is saturated with oil causes low discharge superheat. Low discharge superheat can causes low temperature to the compressor, if the condition goes more low and low then it could damage the compressor too.

What does a low superheat indicate?

The low discharge of a system means refrigerant liquid floods to the compressor for the load is present through the evaporator coil.

When excess amount of refrigerant is enter into the coil or excessive amount of heat present into coil to vaporize the refrigerant properly,that time this condition appear.

Read more about Low Superheat: Important Terms and 3 FAQs

What causes low discharge superheat?

• Flooding to the compressor with the refrigerant liquid through the evaporator coil. The situation mostly happened when the expansion valve overfeeding to the evaporator or faulty of an actuator.
• Pressure is too high.
• Low evaporator air flow.
• Temperature is low.
• The shape of the system is over sized during discharge of a superheated liquid.
• Reduced airflow through the evaporator.
• Due to low cooling water flow or dirty tubes the refrigerant charge may be excess.
• Over charged of refrigerant liquid or oil.

Low discharge superheat trane chiller:

With the help of the compressor’s discharge temperature the inside condition of the refrigeration or air conditioning system easily can be recognize. In other term the discharge temperature describe as a measurement of the superheated refrigerant’s vapour temperature.

Formula-

Discharge Superheat = Temperature of discharge connection – Saturated temperature of the liquid line.

Purpose:

This is used to point an actuator or check the valve issue. The Trane chillers are used to system for improve the efficiency mechanical or electrical to the compressor,deliver the correct amount of the temperature, humidity. During the flooding of the refrigerant liquid or oil the sound of the system is increases, with the Trane chillers the sound became less which impact is good for the environment .The Trane chillers deliver ventilation for the space and also helps to minimize the operating cost.

York yvaa low discharge superheat:

The low discharge superheat faults due to reason of the quantity of oil in the oil separator causes York Yvaa low discharge superheat. For this reason the oil charge is reduced in these specific circuits to correct the nuisance superheat trips. The change is only applicable to the circuits.

Procedure:

• The first step is to identify the unit and the amount of the oil. The oil should be taken as that much quantity with which it could be removed as per the corresponding compressor.
• As per the correct size the compressors are verified.
• Need to walkout the unit.
• After that need to discharge the unit.
• A container is used which should be have measuring indicators gradually.
• In the next step required oil is removed from the container.
• The oil is separate from the compressor on the oil line.
• In the starting if the refrigerant was removed from the low discharge superheat then make sure to correct the refrigerant level.
• Adding the adjusted refrigerant to the system.
• Apply unit to the system.
• For about one hour the unit should be operate at full load.
• Finally need to note down the oil level from the oil separator.

York low discharge superheat:

Low discharge superheat usually the situation occurs because of overcharge of refrigerant or overcharge of oil. Both condition gives lower discharge temperature. Once the refrigerant is saturated with oil low discharge will continue to occur.

Low discharge superheat sensor:

In the low discharge superheat all chillers will have a certain amount of the oil in the refrigerant, a little amount of oil is good but the system but too much is not good for the entire system. An excess amount of present of oil can cut blade from the impeller and reduce the efficiency of the compressor and also minimize the percentage of the heat transfer. For the recovery from this unwanted situation in the low discharge superheat’s chillers recovery equipment is needed, the recovery equipment is called the low discharge superheat sensor.

The main purpose of the sensor is to sense the oil which is float on the top of the refrigerant. The low discharge superheat condition is happened when the refrigerant liquid flooding into the compressor, or in the case of screw compressor, low cold oil temperature.

Low discharge superheat in chiller :

In the application field after doing the investigation we could find that the performance of the chillers attached with an electronic expansion valve. The chillers mainly work in steady state and transient condition. .The chillers capacity works in both hot and cold starts.

In low pressure the chillers start to work, at this condition the refrigerant enter to the evaporator. In case of low discharge superheat the capacity is very fast. In the cooling condition the chillers leading to low off/on cycling losses. The expansion valve works on the both steady and transient state of the chillers.

The capacity of the chillers is about 25 kW.  The chillers mainly consists four components. The components are compressor, evaporator, expansion unit and condenser. Every chillers system has refrigerant.

What is good discharge superheat?

The temperature of the ideal discharge superheat is about 10K-15K.

Frequently Asked Questions:

Q.What is low discharge superheat?

When a little amount of air could passes to the system for the reason of stopping the head load entry through the evaporator coils,which occur low discharge superheat.

The low discharge indicates that the quantity of refrigerant liquid or oil present in the compressor.

Dive into our comprehensive guide designed to clarify your doubts on ‘How to Calculate Superheat.’ This article provides step-by-step instructions, practical examples, and essential tips to accurately measure superheat in various systems, ensuring a clear understanding of this crucial HVAC concept.

It is calculated by obtaining the difference between two temperatures. The one temperature is the outlet temperature of the evaporator, and the second temperature is converted with pressure.

The temperature measurement is done by using the contact type thermometer.

The superheat level indicates the level of the refrigerant present in the evaporator. If the superheat is higher than the average level, the refrigerant is less than the required level in the evaporator.

The following are the reason for the lower refrigerant in the system,

• The technician has charged low refrigerant than an actual level requirement
• the device resists refrigerants like orifices, thermocouples etc.
• The heat load on the evaporator is higher than the average level

How to calculate target superheat?

The target superheat of the air conditioning system can be obtained by the following.

The target can be calculated with wet bulb temperature near to evaporator inlet and the outside dry bulb temperature.

After obtaining both temperatures, the following formula calculates the target superheat.

Target superheat = (3 * Wet bulb temperature – 80 – Dry bulb temperature)/2

The instrument used for the indoor wet bulb temperature measurement is a digital psychrometer. The instrument used for outside dry bulb temperature measurement is the digital temperature measuring instrument.

The dry bulb temperature remains same in the most case. The target can vary with the change in the wet bulb temperature. At the time of refrigerant charging, the wet bulb temperature is changing.

To obtain proper refrigerant charging, the target superheat is maintained near the actual superheats.

Lets’s understand target superheat with the following calculation,

Suppose, Wet bulb temperature = 64 ° F

Dry bulb temperature = 86 ° F

An equation to calculate target superheat

Target superheat = (3 * Wet bulb temperature – 80 – Dry bulb temperature)/2

Target superheat = (3 * 64 – 80 – 86)/2

Target superheat = (192 – 80 – 86)/2

Target superheat = (26)/2

Target superheat = 13° F

How to calculate superheat in a freezer?

The calculation of the superheat in the freezer is similar to the refrigerator.

The superheat in the freezer is the difference between saturation temperature and freezer outlet temperature.

A pressure-temperature chart obtains the saturation temperature. The evaporator’s outlet temperature is measured with a digital thermocouple. Take the difference between both temperatures.

The answer to the difference is the value of the superheat for the freezer.

How to calculate superheat in a chiller?

The superheat of the chiller can be calculated with the following steps

• Identify the suction line for measurement of pressure.
• To obtain the pressure of the suction line, Fix the pressure gauge near the condenser coil.
• Attach the thermocouple at the outlet of the evaporator coil. The service port is provided for the thermocouple.
• Note the reading of pressure after the system achieves steady flow.
• Note the reading of the temperature at the same time.
• Convert the reading of pressure into the corresponding temperature using a pressure-temperature saturation chart.
• Take the difference between the corresponding temperature and the evaporator’s outlet temperature reading.
• The answer to the difference is the value of the superheat.

This process of calculating the superheat remains the same for refrigeration and another similar system.

How to calculate superheat on a heat pump?

The heat pump is functioning opposite to the refrigerant. The superheat can be calculated with the following steps.

• Identify the suction line in the system as the suction line always has more cross-sectional area than another line
• To measure the suction line pressure in the system, install the pressure gauge neat to the condenser coil.
• Attach the temperature measuring device to the outlet of the evaporator coil. The service port is provided for the measuring device.
• Note the reading of pressure after the system achieves steady flow.
• Note the reading of the temperature at the same time.
• Convert the reading of pressure into the corresponding temperature using a pressure-temperature saturation chart.
• Take the difference between the corresponding temperature and the evaporator’s outlet temperature reading.
• The answer to the difference is the value of the superheat.

This process of calculating the superheat remains the same for refrigeration and another similar system.

For example :

If the low side pressure reading of the gauge is 120 PSIG.

The corresponding conversion of the pressure into temperature with a pressure-temperature chart. The value of temperature is 42 ° F.

The temperature measurement at the outlet of the evaporator is 50 ° F.

Now, take a difference between the corresponding temperature and the saturation temperature at the evaporator.

Superheat = Corresponding temperature at the low side – Temperature measured at the evaporator

Superheat = 50 – 42

Superheat = 8 ° F

So, With these simple steps, we can calculate the superheat of the system. The superheat in this example is 8 ° F.

How to calculate evaporator superheat?

The evaporator superheat calculation remains the same as in the refrigerator.

It is a difference between the measured evaporator outlet temperature and the corresponding saturation temperature.

The vapour line temperature is measured by identifying the large cross-section of the suction line. The temperature measurement is not the same in the refrigeration and the air conditioning.

The temperature and the low side pressure of the system are measured after achieving the steady flow condition. The measurement of the system will change if measured immediately after starting.

How to calculate superheated steam temperature?

The superheated steam is generally generated in the higher pressure boiler.

The degree of superheat is obtained by using either a steam table or Mollier diagram. The energy is required to raise the temperature of the saturated steam.

The temperature of the superheated steam is always greater than 100 ° C at the standard pressure condition.

How to calculate superheat R22?

The superheat in the system with R22 is calculated by the following equation

Total Superheat with R22 = Corresponding temperature at suction pressure – Temperature measured at a suction line or outlet of the evaporator

The superheat is nearby 10 ° F  in most cases. If the superheat is high, then it causes an increase in the heat of compression. This increase in temperature can affect the performance of the compressor. It is required to maintain and monitor the superheat continuously on the system.

How to calculate superheat 404a?

There are two types of superheat in the refrigeration system.

Total Superheat with R404a = Corresponding temperature at suction pressure – Temperature measured at a suction line or outlet of the evaporator

The refrigeration system can be analyzed with evaporator superheat, and the compressor superheat. The evaporator superheat always less than the compressor superheat. The compressor superheat also called the total superheat.

To obtain total superheat for R404, one has to measure temperature at the inlet of temperature with a temperature measuring device. Also, measure the pressure at that location.

The compressor superheat is the sum of the evaporator superheat and vapour line or suction line superheat.

The range of low side pressure for the R404 is nearby 20 psig in the usual case, and the inlet temperature of the compressor is 25° C approx.

For the safe operation of a system with R404 refrigerant, the recommended superheat should be in the range of 20° C to 30° C. If the superheat with R404 is more than the above value, then it can deteriorate the performance of the compressor or system.

The thermal expansion valve is the device used to control the superheat in the refrigeration system. The expansion of TXV can control the evaporator superheat. It can reduce the total superheat at the desired level for efficient working of the system.

How to calculate superheat 410a?

The superheat in the system with R410a is calculated by the following equation

Total Superheat with R410a = Corresponding temperature at suction pressure – Temperature measured at a suction line or outlet of the evaporator

To obtain total superheat for R410a, one must measure temperature at the inlet of temperature with a temperature measuring device. Also, measure the pressure at that location.

This article discusses about bending stress formula for different types of beam configurations. We all know that when an object curves due to application of load then it is said to be subjected under bending.

It is very important to know the amount of bending stress being experienced by the work piece. The work piece will break if the applied bending stress exceeds more than the maximum allowable bending stress. The bending strength of the material is the maximum amount of bending strength that can be applied on the work piece before the work piece starts to fracture.

What is bending stress?

Let us start our discussion with the definition of bending stress. It is simply the stress which is responsible for bending of the work piece.

In further sections we shall see the mathematical forms of bending stress for various beam configurations and cross sectional shapes.

What is a beam?

A beam is a structural element that is mainly used for supporting the primary structure. The beam is not necessarily a support, it can itself be a structure for example bridges and balconies.

Most commonly used beams in industry are cantilever beams, simply supported beams and continuous beams.

Bending stress formula for beam

The bending stress depends on the bending moment moment of inertia of cross section and the distance from the neutral axis where the load is applied.

Mathematically, it can be represented as-

σ = My/I

y it he distance from the neutral axis

I is the moment of inertia of cross section

In terms of section modulus-

σ = M/Z

where,

Z is the section modulus of the beam

M is the bending moment

Bending stress formula units

The formula of bending stress can be given as-

σ = My/I

The formula in terms of units of each quantity can be given as-

Units = N – mm x mm/mm⁴

From above, we can derive that the units of bending stress is-

Units = N/mm²

Allowable bending stress formula

The allowable stress is the value of stress beyond which stress should not be applied for safety reasons. The allowable bending stress depends on the flexural rigidity of the material.

The allowable bending stress formula can be given as-

σ_allowable = σ_max/F_s

where,

Fs is the factor of safety

Bending stress formula derivation

Let us consider a beam section as shown in the diagram below-

Let us assume a moment, M is applied on the beam. The beam curves by an angle theta and makes a radius of curvature R as shown in figure below-

The strain in neutral axis is zero. Whereas the strain acting on the line where force is applied experiences strain. Balancing all strain values we get total strain,

(R + y)θ – Rθ/Rθ = y/R

Strain is also given by-

Strain = σ/E

from above equations we can conclude that,

σ/y = E/R

Now,

M = Σ E/R x y²

and,

δA = E/R Σ y² δA

M = E/R x I

From above equations we conclude that,

σ/y = E/R = M/I

Hence derived.

Bending stress formula for rectangular beam

Depending upon the cross section of the beam, the moment of inertia changes and hence the bending stress formula.

The moment of inertia of rectangle is given as-

I = bd³/12

From above, bending stress formula for a rectangular beam can be written as-

σ = 6M/ bd²

Bending stress formula for hollow rectangular beam

Hollow beams are used to reduce the weight of the beam. These beams can be used in light weight applications.

Let us consider a beam with hollow rectangular cross section with outside length as D and inner length as d, outside breadth as B and inner breadth as b.

The section modulus of this cross section will be-

Z = 1/6D x (BD³ – bd³)

Hence the bending stress formula for a hollow beam can be given by-

σ = 3M/(BD³ – bd³)

Bending stress formula for circular cross section

Let us consider a beam having a circular cross section of diameter D.

The moment of inertia of circular section can be given by-

I = πD⁴/64

From above, we can write the bending stress formula for circular beam as-

σ = 32M/ bd³

Bending stress formula for hollow shaft

Let us consider a hollow circular shaft having inner diameter d and outside diameter D.

The moment of inertia of hollow circular section can be given as-

I = π (D⁴-d⁴)/64

From above, the bending stress can be written as-

σ = 32MD/π(D⁴-d⁴)

Bending stress formula for pipe

A pipe is simply a hollow circular shaft. So the bending stress formula is same as that of hollow circular shaft.

That is,

σ = 32MD/π(D⁴-d⁴)

Maximum bending stress for simply supported beam

The general formula for bending stress remains the same that is-

σ = My/I

However, the formula is modified as per the type of loading. The loading can be in the form of point load, uniformly distributed load or uniformly variable load. In further sections we shall see the different formulae for simply supported beams in different forms of loading.

What is bending moment?

The reaction induced in a structural element or the bending effect produced when an external load is applied on the beam (structural element).

Bending moment formula for different beam configurations under different types of loading is discussed in below sections.

Bending moment formula for fixed beam

A fixed beam is a type of beam which is fixed at both the ends. At both the ends the reaction forces are present. The bending moment formula for fixed beam under different types of loading is given below-

• Bending moment under UDL or Uniformly distributed load

The formula for bending moment of fixed beam under UDL is given as-

M = ωL²/12

• Bending moment under point load

The formula for bending moment of fixed beam under point load is given as-

M = ωL/8

• Bending moment under trapezoidal load or UVL or uniformly variable load

The formula for bending moment of fixed beam under trapezoidal load is given as-

M₁ = ωL²/30

For other side,

M₂ = ωL²/20

Bending moment formula for continuous beam

The bending moment of continuous under different types of loading is shown below-

• Bending moment under UDL

To find the bending moment of continuous beam under uniformly distributed load, we need to find the reaction forces at the end points. After that we have to apply equilibrium conditions that is sum of all horizontal and vertical forces is zero as well as moments is zero. To solve UDL, we multiply the length with the magnitude of UDL. For example, if 2N/m of UDL is applied till 4m length of work piece then the net load acting will be 2×4= 8N at center that is at 2m.

• Bending moment under point load

The procedure is same as for UDL. The only difference is that here we know the magnitude of force and the distance at which it is acting so we need not convert it into point load as we did for UDL.

• Bending moment under UVL or uniformly varied load

To solve UVL, we need to find the area of the triangle formed by UVL. The area is the magnitude of point load that will be acting due to UVL. The distance from vertex will be L/3 at which the point load will act. Rest of the procedure is discussed above.

Bending moment formula for rectangular beam

Bending moment of the beam does not depend on the shape of the beam. The bending moment will change as per the loading conditions and the type of beam (whether continuous, cantilever simply supported etc).

Only the moment of inertia changes with the shape of the cross section of the beam. This way the bending stress formula changes. The bending stress formula for rectangular cross section is discussed in above section.

Bending moment formula for UDL

UDL or uniformly distributed load is the type of load which is applied to a certain length of the work piece and is equal in magnitude wherever applied.

The bending moment formula for UDL of different beam configurations are given below-

• For simply supported beam-

The formula for bending moment of simply supported beam under UDL is given as-

M = ωL²/8

• For cantilever beam-

The formula for bending moment of cantilever beam under UDL is given as-

M = ωL²/2

Bending moment formula for point load

Point load is the type of load which acts only at a particular point on the surface of the work piece.

The bending moment formulae for point loads for different beam configurations are given below-

• For simply supported beam: The formula for bending moment of simply supported beam under point load is given as- M = ωL/4

• For cantilever beam: The formula for bending moment of cantilever beam under point load is given as- M = ωL

For other beam configurations, the formula for bending moment is discussed in above sections.

Bending moment formula for trapezoidal load

Trapezoidal load is a type of load which is applied to a certain length of the work piece and varies linearly with length. Trapezoidal load is combination of both UDL and UVL. Lets assume magnitude of UDL as zero to ease our calculations.

The bending moment for different beam configurations under trapezoidal load are given below-

• For simply supported beam– The bending moment of simply supported beam under trapezoidal load is given as- M = ωL²/12

• For cantilever beam– The bending moment of cantilever beam under trapezoidal load is given as- M = ωL²/6

For other beam configurations, the formula is discussed in above section

Summary of bending moment formula

Table below shows a brief summary of formula for different beam configurations under different types of loading

Summary of bending stress formula

Table below shows a brief summary of formula for bending stresses of different beam cross sections