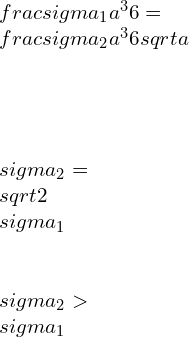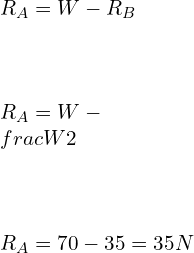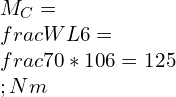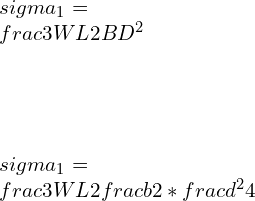Introduction to the Brayton Cycle
The Brayton Cycle, also known as the gas turbine cycle, is a thermodynamic cycle used in power generation and jet engines. It is named after George Brayton, an American engineer who patented the first version of the cycle in 1872. The Brayton Cycle is widely used in gas turbines, which are commonly found in aircraft engines, power plants, and even some automobiles.
Definition of the Brayton Cycle
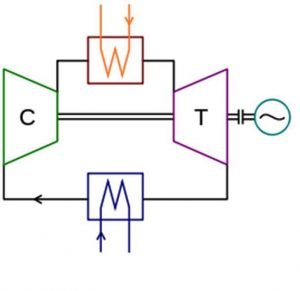
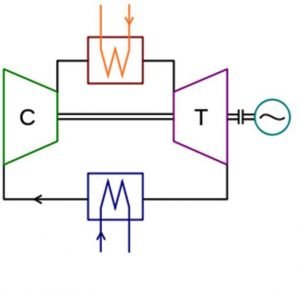
The Brayton Cycle is a closed-loop thermodynamic cycle that consists of four main components: a compressor, a combustion chamber, a turbine, and a heat exchanger. It operates on the principles of the ideal gas law and follows a series of processes to convert thermal energy into mechanical work.
The cycle begins with the compressor, which takes in ambient air and compresses it to a higher pressure. This compressed air then enters the combustion chamber, where fuel is injected and ignited. The resulting high-temperature and high-pressure gases expand, driving the turbine. The turbine extracts energy from the expanding gases, converting it into mechanical work to drive the compressor and any external load, such as an aircraft’s propeller or a power generator.
The exhaust gases from the turbine then pass through a heat exchanger, where they transfer some of their heat to the incoming air before being expelled to the atmosphere. This heat exchange process increases the overall efficiency of the cycle by preheating the air before it enters the combustion chamber.
Diagram of the Brayton Cycle
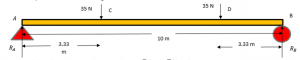
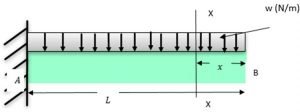
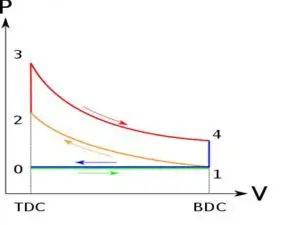
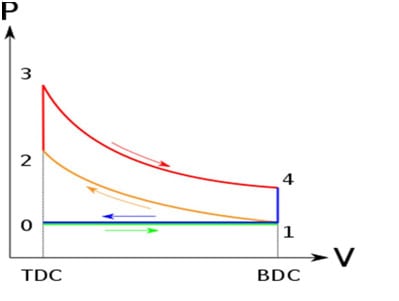
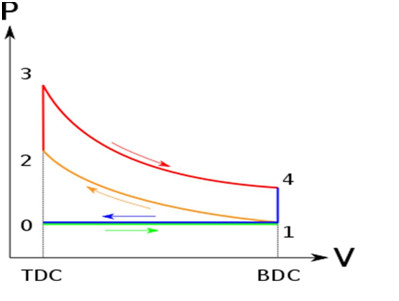
To better understand the Brayton Cycle, let’s take a look at a simplified diagram of the cycle:

As shown in the diagram, the cycle consists of four main processes:
-
Process 1-2 (Isentropic Compression): The compressor takes in ambient air at point 1 and compresses it to a higher pressure at point 2. This process is isentropic, meaning there is no heat transfer or change in entropy.
-
Process 2-3 (Constant Pressure Heat Addition): The compressed air enters the combustion chamber, where fuel is injected and ignited. This process occurs at constant pressure, resulting in a significant increase in temperature.
-
Process 3-4 (Isentropic Expansion): The high-temperature and high-pressure gases from the combustion chamber expand through the turbine, driving it and producing mechanical work. This expansion process is also isentropic.
-
Process 4-1 (Constant Pressure Heat Rejection): The exhaust gases from the turbine pass through a heat exchanger, where they transfer some of their heat to the incoming air. This process occurs at constant pressure, reducing the temperature of the exhaust gases before they are expelled to the atmosphere.
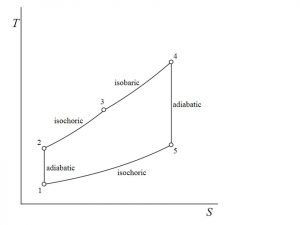
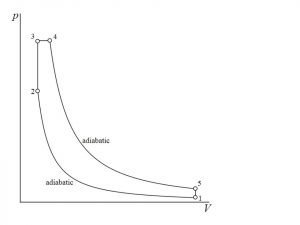
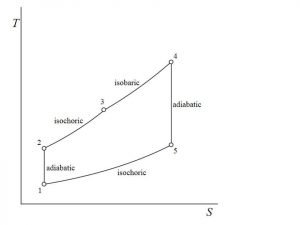
P-V and T-S Diagrams of the Brayton Cycle
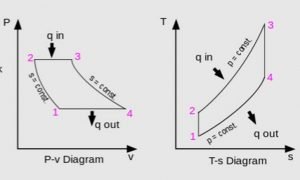
P-V (Pressure-Volume) and T-S (Temperature-Entropy) diagrams are commonly used to visualize the Brayton Cycle. These diagrams provide a graphical representation of the cycle’s processes and help in analyzing its performance.
In the P-V diagram, the vertical axis represents pressure, while the horizontal axis represents volume. The cycle’s processes are represented by lines on the diagram, allowing us to see how pressure and volume change throughout the cycle.
On the other hand, the T-S diagram plots temperature against entropy. It helps us understand the heat transfer and energy exchange that occur during the cycle. The T-S diagram shows the cycle’s processes as curves, allowing us to analyze the changes in temperature and entropy.
Both diagrams provide valuable insights into the performance of the Brayton Cycle, allowing engineers to optimize its efficiency and power output.
In the next sections, we will explore the important relationships within the Brayton Cycle and answer some frequently asked questions about this thermodynamic cycle.
Steps of the Brayton Cycle
The Brayton Cycle is a thermodynamic cycle that is commonly used in gas turbine engines and power generation systems. It consists of four main processes that work together to produce power efficiently. Let’s take a closer look at each step of the Brayton Cycle.
Process 1-2: Reversible Adiabatic Compression
In this first step of the Brayton Cycle, the air is drawn into the compressor, where it is compressed to a higher pressure. The compression process is adiabatic, meaning that no heat is added or removed from the system. As the air is compressed, its temperature increases. This step is crucial as it prepares the air for the subsequent combustion process.
Process 2-3: Constant Pressure Heat Addition
After the air is compressed, it enters the combustion chamber, where fuel is injected and ignited. The high-pressure air from the compressor mixes with the fuel, and combustion occurs. This process is carried out at a constant pressure, allowing for efficient heat transfer from the combustion products to the working fluid. As a result, the temperature and pressure of the working fluid increase significantly.
Process 3-4: Reversible Adiabatic Expansion
Once the air-fuel mixture has undergone combustion and reached its maximum temperature, it enters the turbine. In the turbine, the high-pressure, high-temperature gases expand, driving the turbine blades and producing useful work. The expansion process is adiabatic, meaning that no heat is added or removed from the system. As the gases expand, their temperature and pressure decrease.
Process 4-1: Constant Pressure Heat Rejection
In the final step of the Brayton Cycle, the low-pressure gases from the turbine enter the heat exchanger, where heat is rejected to the surroundings. This process occurs at a constant pressure, allowing for efficient heat transfer. As the gases cool down, their temperature and pressure decrease further, preparing them to re-enter the compressor and start the cycle again.
By following these four processes, the Brayton Cycle can continuously produce power in a gas turbine engine or power generation system. The cycle is highly efficient, as it maximizes the conversion of heat energy into useful work. The thermal efficiency of the Brayton Cycle can be improved by increasing the pressure ratio and temperature ratio, which can be achieved through design modifications and advanced technologies.
In summary, the Brayton Cycle is a fundamental thermodynamic cycle used in gas turbine engines and power generation systems. It consists of four main processes: reversible adiabatic compression, constant pressure heat addition, reversible adiabatic expansion, and constant pressure heat rejection. Each step plays a crucial role in the overall efficiency of the cycle, allowing for the continuous production of power.
Brayton Cycle Refrigeration
Introduction to Brayton Refrigeration Cycle
The Brayton Cycle, also known as the gas turbine cycle, is a thermodynamic cycle that is widely used in power generation, jet engines, and gas turbines. It consists of four main components: compressor, combustion chamber, turbine, and heat exchanger. The cycle operates on the principle of converting thermal energy into mechanical work.
In the context of refrigeration, the Brayton Cycle can be modified to create a refrigeration cycle known as the Brayton Refrigeration Cycle. This cycle utilizes the same components as the traditional Brayton Cycle but with a different configuration. Instead of producing work output, the goal of the Brayton Refrigeration Cycle is to remove heat from a low-temperature reservoir and reject it to a high-temperature reservoir.
The Brayton Refrigeration Cycle is commonly used in cryogenic applications, such as liquefaction of gases and air separation. It offers several advantages over other refrigeration cycles, including high efficiency, compact size, and the ability to achieve very low temperatures.
Inverted Brayton Cycle
The Inverted Brayton Cycle, also known as the Brayton Heat Pump Cycle, is a variation of the traditional Brayton Cycle. In this cycle, the roles of the hot and cold reservoirs are reversed compared to the Brayton Refrigeration Cycle. The goal of the Inverted Brayton Cycle is to absorb heat from a low-temperature reservoir and reject it to a high-temperature reservoir, thus providing heating instead of cooling.
The Inverted Brayton Cycle finds applications in heat pumps, where it can be used for space heating, water heating, and industrial processes. It offers advantages such as high efficiency, low operating costs, and the ability to provide both heating and cooling.
Joule Brayton Cycle
The Joule Brayton Cycle, also known as the simple Brayton Cycle, is the basic form of the Brayton Cycle. It operates on the principle of constant pressure combustion and is commonly used in gas turbine engines. The cycle consists of a compressor, combustion chamber, turbine, and heat exchanger.
In the Joule Brayton Cycle, air is compressed by the compressor, then heated in the combustion chamber where fuel is burned, resulting in a high-temperature, high-pressure gas. This gas expands through the turbine, producing work output, and then passes through the heat exchanger to reject heat to the surroundings. The cycle is then repeated.
The Joule Brayton Cycle is widely used in power generation, where it converts the energy of a fuel into mechanical work to drive a generator. It offers high thermal efficiency and is capable of generating large amounts of power.
Reverse Brayton Cycle
The Reverse Brayton Cycle, also known as the Brayton Cryocooler Cycle, is a modification of the traditional Brayton Cycle that is used for cryogenic cooling applications. In this cycle, the roles of the hot and cold reservoirs are reversed compared to the Brayton Refrigeration Cycle. The goal of the Reverse Brayton Cycle is to absorb heat from a high-temperature reservoir and reject it to a low-temperature reservoir, thus achieving cryogenic temperatures.
The Reverse Brayton Cycle finds applications in cryogenic systems, such as cooling of superconducting magnets, infrared detectors, and medical imaging devices. It offers advantages such as high cooling capacity, compact size, and the ability to achieve very low temperatures.
In conclusion, the Brayton Cycle and its variations play a crucial role in various industries, including power generation, refrigeration, heating, and cryogenics. Each variation of the cycle offers unique advantages and is tailored to specific applications. Understanding the principles and applications of the Brayton Cycle is essential for engineers and researchers working in these fields.
Brayton Cycle vs. Rankine Cycle
Comparison of Brayton Cycle and Rankine Cycle
The Brayton Cycle and Rankine Cycle are two thermodynamic cycles commonly used in power generation and propulsion systems. While both cycles involve the conversion of heat into work, they differ in several aspects.
| Brayton Cycle | Rankine Cycle |
|---|---|
| Used in gas turbine engines and jet engines | Used in steam power plants |
| Operates on an open cycle | Operates on a closed cycle |
| Uses a compressor, combustion chamber, and turbine | Uses a pump, boiler, and turbine |
| Utilizes a gas as the working fluid | Utilizes a liquid (usually water) as the working fluid |
| Higher thermal efficiency | Lower thermal efficiency |
| Higher power-to-weight ratio | Lower power-to-weight ratio |
Differences in Heat Addition and Rejection
One of the key differences between the Brayton Cycle and Rankine Cycle lies in the way heat is added and rejected. In the Brayton Cycle, heat addition occurs in the combustion chamber, where fuel is burned, and the resulting high-temperature gases expand through the turbine, producing work. The heat rejection takes place in the heat exchanger, where the exhaust gases transfer their heat to the surroundings.
On the other hand, the Rankine Cycle involves heat addition in the boiler, where the working fluid is heated by the combustion of fuel. The high-pressure liquid then expands through the turbine, generating work. Heat rejection occurs in the condenser, where the working fluid is cooled and condensed back into a liquid state.
Handling of Low-Pressure Gas
Another notable difference between the Brayton Cycle and Rankine Cycle is the handling of low-pressure gas. In the Brayton Cycle, the low-pressure gas is discharged directly into the atmosphere after passing through the turbine. This open cycle allows for continuous operation without the need for a condenser.
In contrast, the Rankine Cycle is a closed cycle, which means the low-pressure liquid is pumped back to the boiler to be reheated and undergo the cycle again. This closed-loop system requires the use of a condenser to cool and condense the working fluid back into a liquid state before it is pumped back to the boiler.
Overall, while both the Brayton Cycle and Rankine Cycle are thermodynamic cycles used for power generation, they differ in terms of their applications, working fluids, heat addition and rejection processes, and handling of low-pressure gas. Understanding these differences is crucial in designing and optimizing power generation systems and propulsion systems for various applications.
Brayton Cycle Explained
The Brayton cycle, also known as the gas turbine cycle, is a thermodynamic cycle used in power generation and jet engines. It consists of four main components: a compressor, a combustion chamber, a turbine, and a heat exchanger. In this section, we will explore the different aspects of the Brayton cycle, including its ideal form, derivation and analysis, regeneration, and modifications for actual applications.
Ideal Brayton Cycle and Thermal Efficiency
The ideal Brayton cycle is a theoretical model that assumes perfect conditions and no losses. It consists of two reversible adiabatic processes and two isobaric processes. The cycle starts with the compression of air by the compressor, followed by the addition of heat in the combustion chamber. The high-pressure and high-temperature gases then expand through the turbine, producing work output. Finally, the gases are cooled in the heat exchanger before returning to the compressor.
The thermal efficiency of the ideal Brayton cycle can be calculated using the temperature and pressure ratios. The temperature ratio, denoted by T3/T2, represents the ratio of the turbine inlet temperature to the compressor inlet temperature. The pressure ratio, denoted by P3/P2, represents the ratio of the turbine inlet pressure to the compressor inlet pressure. The thermal efficiency, denoted by ηth, is given by the formula:
ηth = 1 – (1 / (P3/P2)((γ-1)/γ))
where γ is the specific heat ratio of the working fluid.
Derivation and Analysis of Brayton Cycle
To derive the Brayton cycle, we consider the first law of thermodynamics and apply it to each component of the cycle. By assuming ideal gas behavior and neglecting kinetic and potential energy changes, we can derive the expressions for work and heat transfer in each process. This allows us to analyze the performance of the cycle and calculate important parameters such as the work output and heat input.
The analysis of the Brayton cycle involves evaluating the net work output, thermal efficiency, and specific work output. These parameters depend on the pressure ratio, temperature ratio, and specific heat ratio of the working fluid. By varying these ratios, we can optimize the cycle for different applications, such as power generation or aircraft propulsion.
Brayton Cycle with Regeneration


Regeneration is a technique used to improve the thermal efficiency of the Brayton cycle. It involves recovering some of the waste heat from the exhaust gases and using it to preheat the compressed air before it enters the combustion chamber. This reduces the amount of fuel required to reach the desired turbine inlet temperature, resulting in higher thermal efficiency.
In a regenerative Brayton cycle, a heat exchanger, known as a regenerator, is placed between the compressor and the combustion chamber. The regenerator transfers heat from the hot exhaust gases to the cold compressed air, increasing its temperature. This preheated air then enters the combustion chamber, where fuel is added and combustion occurs. The rest of the cycle remains the same as the ideal Brayton cycle.
Actual Brayton Cycle and Efficiency Modifications
In real-world applications, the Brayton cycle deviates from the ideal model due to various losses and inefficiencies. These include pressure losses in the compressor and turbine, heat losses to the surroundings, and combustion inefficiencies. To account for these factors, modifications are made to the ideal Brayton cycle to improve its efficiency and performance.
One common modification is the use of intercooling and reheating. Intercooling involves cooling the compressed air between stages of the compressor, reducing its temperature and increasing its density. Reheating, on the other hand, involves adding heat to the gases between stages of the turbine, increasing their temperature and expanding them further. These modifications help to mitigate the effects of irreversibilities and improve the overall efficiency of the cycle.
Another modification is the inclusion of a bypass system, commonly used in aircraft engines. This allows a portion of the compressed air to bypass the combustion chamber and directly mix with the exhaust gases, reducing fuel consumption and increasing thrust.
In conclusion, the Brayton cycle is a fundamental thermodynamic cycle used in gas turbines and jet engines. Understanding its ideal form, derivation, regeneration, and modifications is crucial for optimizing its performance and efficiency in various applications. By continuously improving and refining the Brayton cycle, engineers can enhance power generation, propulsion systems, and other industrial processes.
Frequently Asked Questions (FAQ) about the Brayton Cycle
How to Increase Efficiency of Brayton Cycle
The efficiency of the Brayton cycle, also known as the gas turbine cycle, can be improved by implementing certain measures. Here are some ways to increase the efficiency of the Brayton cycle:
-
Increasing the Pressure Ratio: The efficiency of the Brayton cycle is directly proportional to the pressure ratio. By increasing the pressure ratio, the cycle can extract more work from the same amount of heat input, resulting in higher efficiency.
-
Increasing the Temperature Ratio: Similar to the pressure ratio, increasing the temperature ratio also improves the efficiency of the Brayton cycle. This can be achieved by using more efficient combustion techniques or by utilizing advanced materials that can withstand higher temperatures.
-
Utilizing Regenerative Heating: In a regenerative Brayton cycle, a heat exchanger is used to preheat the compressed air before it enters the combustion chamber. This reduces the amount of heat required in the combustion process, resulting in improved efficiency.
-
Optimizing the Compressor and Turbine Design: The efficiency of the compressor and turbine plays a crucial role in the overall efficiency of the Brayton cycle. By optimizing the design and using advanced materials, the losses in these components can be minimized, leading to higher efficiency.
Application of Brayton Cycle
The Brayton cycle finds its application in various fields, including power generation and jet engines. Here are some key applications of the Brayton cycle:
-
Gas Turbines: Gas turbines are widely used in power generation, aviation, and industrial applications. The Brayton cycle forms the basis of gas turbine engines, where the combustion of fuel produces high-temperature gases that drive the turbine, generating power or thrust.
-
Jet Engines: Jet engines, commonly used in aircraft, also operate on the Brayton cycle. The incoming air is compressed, mixed with fuel, and ignited in the combustion chamber. The resulting high-velocity exhaust gases propel the aircraft forward, providing thrust.
-
Power Generation: Gas turbine power plants utilize the Brayton cycle to generate electricity. The combustion of fuel in the gas turbine produces high-pressure and high-temperature gases that drive the turbine, which is connected to a generator, converting mechanical energy into electrical energy.
Brayton Cycle Problems and Solutions
While the Brayton cycle offers numerous advantages, it also presents some challenges. Here are some common problems encountered in the Brayton cycle and their solutions:
-
Compressor Surge: Compressor surge occurs when the flow rate through the compressor decreases abruptly, leading to a disruption in the cycle’s operation. To prevent compressor surge, anti-surge control systems are employed, which regulate the flow and maintain stable compressor operation.
-
Combustion Instability: Combustion instability can cause fluctuations in the flame, leading to reduced efficiency and increased emissions. Advanced combustion techniques, such as lean premixed combustion, are employed to mitigate combustion instability and improve overall performance.
-
Heat Exchanger Fouling: Fouling of the heat exchanger surfaces can reduce the efficiency of the Brayton cycle. Regular maintenance and cleaning of the heat exchanger surfaces help prevent fouling and ensure optimal heat transfer.
Power Calculation and Compressor Efficiency
Calculating the power output and compressor efficiency is essential to assess the performance of the Brayton cycle. Here’s how these parameters are determined:
-
Power Calculation: The power output of the Brayton cycle can be calculated using the equation: Power Output = Mass Flow Rate * Specific Work Output. The mass flow rate is the rate at which air passes through the cycle, and the specific work output is the work done by the turbine per unit mass of air.
-
Compressor Efficiency: Compressor efficiency is a measure of how effectively the compressor compresses the air. It is calculated as the ratio of the actual work done by the compressor to the ideal work done. Compressor efficiency can be improved by optimizing the compressor design and reducing losses.
Comparison of Simple and Regenerative Brayton Cycles
The Brayton cycle can be implemented in two configurations: simple and regenerative. Here’s a comparison between the two:
| Parameter | Simple Brayton Cycle | Regenerative Brayton Cycle |
|---|---|---|
| Heat Exchanger | Not present | Present |
| Preheating of Compressed Air | Not applicable | Achieved through a heat exchanger |
| Efficiency | Lower efficiency compared to regenerative cycle | Higher efficiency due to preheating of compressed air |
| Implementation Complexity | Simple | More complex |
| Cost | Relatively lower cost | Higher cost due to the additional heat exchanger |
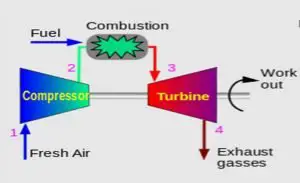
Brayton Cycle in Gas Turbines
The Brayton cycle forms the basis of gas turbine engines used in power generation and aviation. Here’s how the Brayton cycle is implemented in gas turbines:
-
Compressor: The incoming air is compressed by the compressor, increasing its pressure and temperature.
-
Combustion Chamber: The compressed air is mixed with fuel and ignited in the combustion chamber, resulting in the release of high-temperature gases.
-
Turbine: The high-temperature gases expand through the turbine, driving its blades and extracting work to generate power or thrust.
-
Exhaust: The exhaust gases, after passing through the turbine, are expelled into the atmosphere, completing the Brayton cycle.
Gas turbines offer high power-to-weight ratios, making them suitable for applications where weight and size are critical factors, such as aircraft propulsion and mobile power generation.
In conclusion, the Brayton cycle, with its various applications and potential for efficiency improvements, plays a vital role in power generation and aviation. Understanding the key concepts, challenges, and solutions related to the Brayton cycle is essential for optimizing its performance and exploring future advancements in this thermodynamic cycle.
Frequently Asked Questions
Q: What is the Brayton cycle?
A: The Brayton cycle, also known as the gas turbine cycle, is a thermodynamic cycle used in power generation and jet engines. It consists of four main components: a compressor, combustion chamber, turbine, and heat exchanger.
Q: What are the steps involved in the Brayton cycle?
A: The Brayton cycle involves four steps: compression, combustion, expansion, and exhaust. During compression, the air is compressed by the compressor. In the combustion step, fuel is added and ignited in the combustion chamber. Expansion occurs as the high-pressure gas passes through the turbine, generating work output. Finally, the exhaust step involves releasing the remaining gas to the environment.
Q: How does the Brayton cycle work in refrigeration?
A: The Brayton cycle can be used in refrigeration systems by reversing the direction of heat transfer. Instead of generating power, the cycle absorbs heat from a low-temperature source and rejects it to a high-temperature sink, providing cooling.
Q: Why is 1 Decembrie not considered in the FAQ terms?
A: The term “why not 1 Decembrie” is not relevant to the topics of Brayton cycle, gas turbine cycle, or power generation. Therefore, it is not included in the FAQ terms.
Q: What is the difference between the Brayton cycle and the Rankine cycle?
A: The Brayton cycle is an open cycle used in gas turbines, while the Rankine cycle is a closed cycle used in steam power plants. The Brayton cycle uses air or gas as the working fluid, while the Rankine cycle uses water or steam.
Q: What are the working principles of the Brayton cycle?
A: The working principles of the Brayton cycle involve compressing the working fluid, adding heat through combustion, expanding the fluid to generate work, and then exhausting the fluid. This cycle enables the conversion of thermal energy into mechanical work.
Q: Can you explain the Brayton cycle in more detail?
A: Certainly! The Brayton cycle starts with the compression of air by a compressor, increasing its pressure and temperature. The compressed air then enters the combustion chamber, where fuel is added and ignited, resulting in a high-temperature gas. This gas expands through the turbine, producing work output. Finally, the exhaust gas is released, and the cycle repeats.
Q: What is the role of gas turbines in the Brayton cycle?
A: Gas turbines are the key components of the Brayton cycle. They consist of a compressor, combustion chamber, and turbine. The compressor compresses the air, the combustion chamber adds fuel and ignites it, and the turbine extracts work from the expanding gas.
Q: How does the pressure ratio affect the Brayton cycle?
A: The pressure ratio, defined as the ratio of the compressor outlet pressure to the inlet pressure, affects the performance of the Brayton cycle. A higher pressure ratio leads to increased thermal efficiency and work output, but it also requires a more robust and efficient compressor.
Q: How is the thermal efficiency of the Brayton cycle calculated?
A: The thermal efficiency of the Brayton cycle is calculated as the ratio of the net work output to the heat input. It can be expressed as the difference between the compressor and turbine work divided by the heat input from the combustion chamber.
![Rendered by QuickLaTeX.com \\eta_{dual}=1-\\frac{1}{r_k^{\\gamma -1}}[\\frac{r_pr_c^\\gamma -1}{(r_p-1)+r_p\\gamma (r_c-1)}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ef5d62cb8110d7b8f13b61f35836bb06_l3.png)

![Rendered by QuickLaTeX.com \\\\\\eta=1-\\frac{(T_5-T_1)}{([T_3-T_2 ]+\\gamma[T_4-T_3])}\\\\\\\\ \\eta_{dual}=1-\\frac{1}{r_k^{\\gamma -1}}[\\frac{r_pr_c^\\gamma -1}{(r_p-1)+r_p\\gamma (r_c-1)}]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-8d7a6e6fd77001105b5968b92751f278_l3.png)
![Rendered by QuickLaTeX.com M.E.P=\\frac{(P_1 [\\gamma r_p r_k^\\gamma (r_c-1)+r_k^\\gamma (r_p-1)-r_k (r_p r_c^\\gamma-1) ] )}{(\\gamma-1)(r_k-1) }](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-b84ee279a3d25c3e77b699126299c702_l3.png)

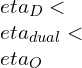

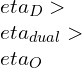

![Rendered by QuickLaTeX.com \\\\Q_v=C_v [T_3-T_2 ]=0.718*[1199-671]=379kJ/kg\\\\\\\\ (2/3)*Q=Q_v\\\\\\\\ Q=(3/2)*379=568.5 kJ/kg\\\\\\\\ C_p [T_4-T_3 ]=Q/3\\\\\\\\ 1.005*[T_4-1199]=568.5/3\\\\\\\\ T_4=1387.55 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-16101adc0e9d29571aa2ae5394d2b62b_l3.png)

![Rendered by QuickLaTeX.com \\\\r_c=[T_4/T_3 ]=[1873/1433]=1.307\\\\\\\\ Also \\;\\\\\\\\ r_c=[V_4/V_3] =1.307\\\\\\\\ V_4=1.307*0.004=5.228*10^{-3} m^3](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-b809892b3aac2d862e3a5f4e08ca9735_l3.png)
![Rendered by QuickLaTeX.com \\\\T_5/T_4 =[V_4/V_5] ^{\\gamma-1}\\\\\\\\ (T_5/1873)=[\\frac{(5.228*10^{-3})}{0.07}]^{1.4-1}\\\\\\\\ T_5=663.48 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-3c2788b7142d2658ebd2be9ada56a46a_l3.png)
![Rendered by QuickLaTeX.com \\\\Q_s=C_v [T_3-T_2 ]+C_p [T_4-T_3 ]\\\\\\\\ Q_s=0.717*(1433-942.6)+1.005*(1873-1433)\\\\\\\\ Q_s=793.81 kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-e98662763e1036e6adb2d3e4c2f5db76_l3.png)




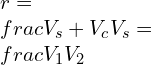


![Rendered by QuickLaTeX.com \\\\\\eta=1-\\frac{[T_4-T_1]}{[T_3-T_2]}\\\\\\\\ \\frac{T_2}{T_1}=\\frac{T_3}{T_4}\\\\\\\\ \\frac{T_4}{T_1}=\\frac{T_3}{T_2}\\\\\\\\ \\eta=1-\\frac{1}{r^{\\gamma-1}}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f49c7bd3e52c0f607a4e2c504e1ab46b_l3.png)

![Rendered by QuickLaTeX.com \\\\1000=0.717*[473-1188+T_3-T_4]\\\\\\\\ 1000=0.717*[473-1188+2.512 T_4-T_4]\\\\\\\\ T_4=1395 K](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-7b3a245ad98e31383d6f4d9583e34a18_l3.png)
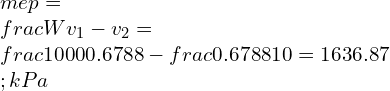
![Rendered by QuickLaTeX.com \\\\\\frac{\\mathrm{d} C_v}{C_v}=0.02\\\\\\\\ \\eta=1-\\frac{1}{r^{\\gamma -1}}=1-\\frac{1}{6^{1.4 -1}}=0.511\\\\\\\\ \\gamma -1=\\frac{R}{C_v}\\\\\\\\ \\eta=1-[\\frac{1}{r}]^\\frac{R}{C_v}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-757291f702fb1983830f344901562518_l3.png)
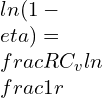
![Rendered by QuickLaTeX.com \\\\\\frac{d\\eta}{1-\\eta}=\\frac{-R}{C_v^2}*dC_v*ln[1/r]\\\\\\\\ \\frac{d\\eta}{1-\\eta}=\\frac{-R}{C_v}*\\frac{dC_v}{C_v}*ln[1/r]\\\\\\\\ \\frac{d\\eta}{\\eta}=\\frac{1-\\eta}{\\eta}*\\frac{-R}{C_v}*\\frac{dC_v}{C_v}*ln[1/r]\\\\\\\\ \\frac{d\\eta}{\\eta}=\\frac{1-0.511}{0.511}*\\frac{-0.287}{0.718}*0.02*ln[1/6]\\\\\\\\ \\frac{d\\eta}{\\eta}=-0.0136\\\\\\\\ \\frac{d\\eta}{\\eta}*100=-0.0136*100=-1.36\\%](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ef306304ee4e226f05089530564c7534_l3.png)

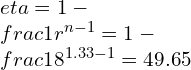
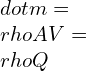
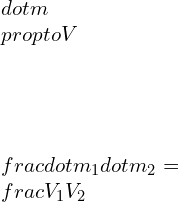
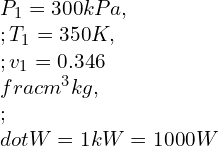
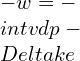
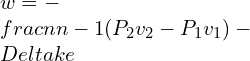
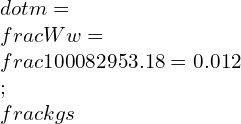
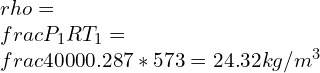
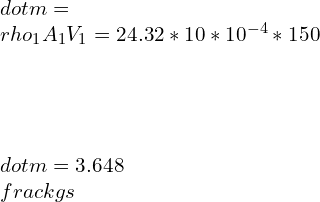
![Rendered by QuickLaTeX.com \\\\\\dot{m}h_1+Q=\\dot{m}h_2+W\\\\ \\\\\\dot{m}[h_1-h_2]=W-Q\\\\ \\\\\\dot{m}C_p[T_1-T_2]=W-Q\\\\ \\\\\\dot{m}=\\frac{W-Q}{C_p[T_1-T_2]}=\\frac{4600+300}{1100-400}=7\\;\\frac{kg}{s}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-ab801810045c79c44023956f8f7184db_l3.png)


![Rendered by QuickLaTeX.com \\\\P=\\dot{m}[h_1-h_2]\\\\ \\\\\\dot{m}=\\frac{P}{h_1-h_2}\\\\ \\\\\\dot{m}=\\frac{P}{C_p[T_1-T_2]}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f9d3656cc8e9eecbd79512180f849452_l3.png)
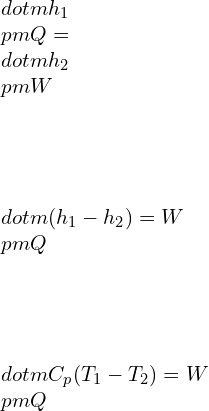
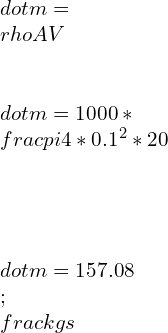


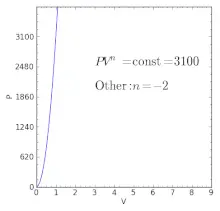

![Rendered by QuickLaTeX.com \\\\P_1V_1^n=P_2V_2^n\\\\ \\\\\\frac{P_2}{P_1}=[\\frac{V_1}{V_2}]^n](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-2f79f958a45d3de1b856d5a94f13b960_l3.png)
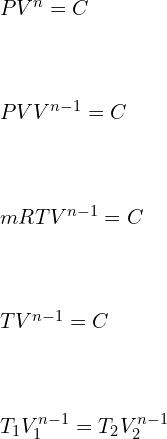
![Rendered by QuickLaTeX.com \\\\W=\\int_{1}^{2}Pdv\\\\ \\\\W=\\int_{1}^{2}\\frac{C}{V^n}dv\\\\ \\\\W=C[\\frac{V^{-n+1}}{-n+1}]^2_1\\\\ \\\\W=\\frac{P_1V_1V_1^{-n+1}-P_2V_2V_2^{-n+1}}{n-1}\\\\ \\\\W=\\frac{P_1V_1-P_2V_2}{n-1}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-34673bf8e32b5351c5b578248dee5bc8_l3.png)
![Rendered by QuickLaTeX.com \\\\dQ=mC_v [T_2-T_1 ]+\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=\\frac{mR}{\\gamma -1} [T_2-T_1 ]+\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=\\frac{P_1 V_1-P_2 V_2}{\\gamma-1}+\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=P_1 V_1 [\\frac{1}{n-1}-\\frac{1}{\\gamma-1}]-P_2 V_2 [\\frac{1}{n-1}-\\frac{1}{\\gamma-1}]\\\\ \\\\dQ=\\frac{\\gamma -n}{\\gamma -1}\\frac{P_1 V_1-P_2 V_2}{n-1}\\\\ \\\\dQ=\\frac{\\gamma -n}{\\gamma -1}W_{poly}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-30c37e1c1015acd433b3e3770a8fe0c2_l3.png)
![Rendered by QuickLaTeX.com H_p=53.3*z_{avg}*\\frac{T_s}{S}(\\frac{\\gamma \\eta _p}{\\gamma -1})[(\\frac{P_d}{P_s})^\\frac{\\gamma -1}{\\gamma \\eta _p}-1]](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-9c919db20c42b8e740e81a820f601ceb_l3.png)

![Rendered by QuickLaTeX.com \\\\W=\\frac{P_1V_1-P_2V_2}{n-1}\\\\W=\\frac{mR[T_2-T_1]}{n-1}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-e851f1e9ecda47f4624cdfbe61caf7a5_l3.png)
![Rendered by QuickLaTeX.com \\\\\\frac{P_1V_1}{T_1} =mR \\\\mR=\\frac{200*10^3*0.1}{200}\\\\ \\\\mR=100 J/(kg. K) \\\\ \\\\W=\\frac{100*[400-200]}{1.22-1}\\\\ \\\\W=90.909 kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-4a2c065006d2428fe2857f0a0f21c6fa_l3.png)
![Rendered by QuickLaTeX.com W=\\frac{1*208.1[90-30]}{1.33-1}\\\\ \\\\W=37.836\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f983a3808c53dd20f2f92333dd859293_l3.png)
![Rendered by QuickLaTeX.com \\\\W=\\frac{10*63.33*[259.63-500]}{1.28-1}\\\\ \\\\W=-543.66\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f3ef4aecd99714fbc6ce8f1b80373ad1_l3.png)
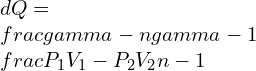

![Rendered by QuickLaTeX.com dQ=\\frac{\\gamma -n}{\\gamma -1}\\frac{mR[T_2-T_1]}{n-1}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-9623d0173cc15e05297ccd524759531a_l3.png)
![Rendered by QuickLaTeX.com \\\\dQ=\\frac{1.4 -1.15}{1.4 -1}\\frac{1*518.2*[311.52-293]}{1.15-1}\\\\\\\\dQ=39.997\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-0ddd733cda78faa73a241c473fe6bf77_l3.png)
![Rendered by QuickLaTeX.com \\\\W=\\frac{2077.1*[400-303]}{1.24-1}=839.494\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-58fbc142958923099feceb48f6431e40_l3.png)

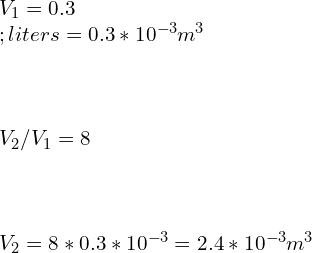
![Rendered by QuickLaTeX.com \\\\\\frac{P_2}{3}=[\\frac{0.3}{2.4}]^{1.7}\\\\\\\\P_2=0.0874\\;MPa](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-a09eba21348fdf1e95edca72e436526b_l3.png)
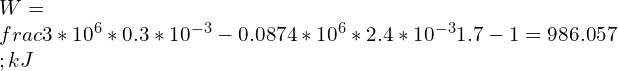
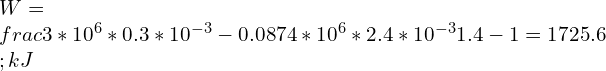
![Rendered by QuickLaTeX.com \\\\\\frac{800}{120}=[\\frac{200}{V_2}]^{1.29} \\\\\\\\V_2=45.95\\;L](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-41323679bbdf82666782c64b16cfa457_l3.png)
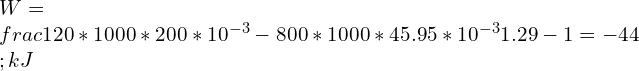
![Rendered by QuickLaTeX.com dQ=\\frac{1.4-1.1}{1.4 -1}\\frac{12*518.2*[30-150]}{1.1-1}=-5.596\\;MJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-6ebe82b84e38a99ceddb14a01559df47_l3.png)
![Rendered by QuickLaTeX.com W=\\frac{1*81.49*[100-10]}{1.33-1}=22.224\\;kJ](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-f99d83d9c42cc7b2180db4866e1d97ed_l3.png)
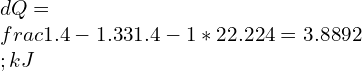
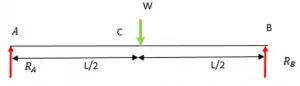
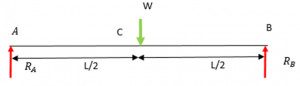

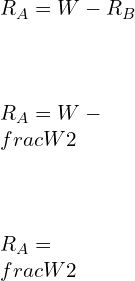



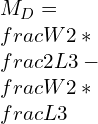
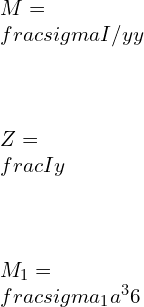
![Rendered by QuickLaTeX.com \\\\I=\\frac{bd^3}{12}*2\\\\ \\\\I=\\sqrt{2}a*[\\frac{a}{\\sqrt{2}}]^3*\\frac{2}{12}\\\\\\\\ \\\\Z=\\frac{I}{y}=\\frac{a^3}{6\\sqrt{a}}\\\\\\\\ \\\\M_2=\\frac{\\sigma _2 a^3}{6\\sqrt{a}}](https://lambdageeks.com/wp-content/ql-cache/quicklatex.com-82a207ef63fe59582dca98a0a941f99d_l3.png)