In physics, finding the constant velocity with friction is an essential skill that allows us to understand the motion of objects in the presence of frictional forces. friction plays a significant role in determining the velocity of an object, and it is crucial to consider its effects when analyzing motion. In this blog post, we will explore how to calculate constant velocity with friction, understand the role of friction force, and clarify common misconceptions related to this topic. So, let’s dive in!
III. How to Calculate Constant Velocity with Friction
A. The Role of Friction Force in Velocity
friction is a force that opposes the motion of an object when it comes into contact with a surface. It arises due to the interaction between the atoms or molecules of two surfaces in contact. When an object is in motion, the frictional force acts in the opposite direction to its velocity. This force can either be static friction or kinetic friction, depending on whether the object is at rest or in motion, respectively.
To calculate constant velocity with friction, we need to consider the effects of both static and kinetic friction. Static friction comes into play when an object is at rest and prevents it from moving until an external force overcomes it. On the other hand, kinetic friction acts when the object is already in motion and opposes its movement.
B. The Importance of the Coefficient of Friction
The coefficient of friction is a dimensionless quantity that represents the interaction between two surfaces in contact. It quantifies the level of friction between the surfaces and helps us calculate the frictional force. There are two types of coefficients of friction: the coefficient of static friction (μs) and the coefficient of kinetic friction (μk).
The coefficient of static friction represents the maximum frictional force between two surfaces before one starts sliding over the other. It is typically denoted by μs and can vary depending on the nature of the surfaces in contact. The coefficient of kinetic friction, denoted by μk, represents the frictional force between two surfaces when they are in relative motion.
C. Steps to Calculate Constant Velocity with Friction
To calculate constant velocity with friction, follow these steps:
- Determine the coefficient of friction (either μs or μk) between the surfaces in contact.
- Identify the forces acting on the object and determine their magnitudes and directions.
- Use Newton’s second law of motion, F = ma, to calculate the net force acting on the object. Take into account both the forces influencing the motion and the frictional force.
- If the object is at rest, calculate the maximum static frictional force using the equation F(static friction) = μs * N, where N is the normal force acting on the object.
- If the object is already in motion, calculate the kinetic frictional force using the equation F(kinetic friction) = μk * N.
- Equate the net force to the product of the object’s mass and acceleration (F = ma) and solve for acceleration.
- Finally, calculate the constant velocity by using the formula v = u + at, where v represents the final velocity, u the initial velocity, a the acceleration, and t the time taken to reach the constant velocity.
IV. Worked Out Examples

Now, let’s work through a few examples to solidify our understanding of how to calculate constant velocity with friction.
A. Example of Calculating Constant Velocity with Given Friction
Suppose we have an object with a mass of 5 kg on a horizontal surface. The coefficient of kinetic friction between the object and the surface is 0.3. If an external force of 20 N is applied to the object, what will be its constant velocity?
First, let’s calculate the kinetic frictional force using the equation F(kinetic friction) = μk * N. Here, the normal force acting on the object is equal to its weight, which is given by N = mg, where m is the mass of the object and g is the acceleration due to gravity (approximately 9.8 m/s^2).
N = 5 kg * 9.8 m/s^2 = 49 N
Next, plug in the values into the equation:
F(kinetic friction) = 0.3 * 49 N = 14.7 N
The net force acting on the object is the difference between the applied force and the kinetic frictional force:
Net force = 20 N – 14.7 N = 5.3 N
Now, use Newton’s second law of motion, F = ma, to find the acceleration:
5.3 N = 5 kg * a
a = 5.3 N / 5 kg = 1.06 m/s^2
Finally, we can calculate the constant velocity using the formula v = u + at, where u is the initial velocity (0 m/s), a is the acceleration (1.06 m/s^2), and t is the time taken to reach constant velocity (which we assume to be a sufficiently long duration):
v = 0 m/s + (1.06 m/s^2) * t
As t approaches infinity, the final velocity (or constant velocity) becomes:
v = 0 m/s + (1.06 m/s^2) * ∞ = 1.06 m/s
Hence, the object will have a constant velocity of 1.06 m/s.
B. Example of Finding Friction Coefficient with Known Velocity
Suppose an object is moving with a constant velocity of 8 m/s on a horizontal surface. The applied force on the object is 30 N, and the mass of the object is 2 kg. What is the coefficient of kinetic friction between the object and the surface?
To find the coefficient of kinetic friction, we need to calculate the kinetic frictional force. Given that the object is moving with a constant velocity, the net force acting on it is zero. Hence, the applied force is equal to the kinetic frictional force:
Applied force = Kinetic frictional force
30 N = μk * N
Since the normal force N is equal to the weight of the object (N = mg), we can rewrite the equation as:
30 N = μk * mg
Divide both sides of the equation by mg:
μk = 30 N / (2 kg * 9.8 m/s^2) ≈ 1.53
Therefore, the coefficient of kinetic friction between the object and the surface is approximately 1.53.
C. Example of Determining Acceleration with Velocity and Friction Coefficient
Let’s consider an object with an initial velocity of 10 m/s on a horizontal surface. The coefficient of kinetic friction between the object and the surface is 0.2. If no external forces act on the object, what will be its acceleration?
Since no external forces act on the object, the only force opposing its motion is the kinetic frictional force. To find the acceleration, we can use Newton’s second law of motion, which states that the net force is equal to the product of mass and acceleration:
Net force = Mass * Acceleration
The kinetic frictional force can be calculated using the equation F(kinetic friction) = μk * N. As mentioned before, the normal force N is equal to the weight of the object (N = mg). Therefore, the equation becomes:
F(kinetic friction) = μk * mg
Substituting the values into the equation, we have:
F(kinetic friction) = 0.2 * mg
Since the net force is equal to the kinetic frictional force:
mg = ma
Rearranging the equation, we find:
a = g
Therefore, the acceleration of the object is equal to the acceleration due to gravity, which is approximately 9.8 m/s^2.
V. Common Misconceptions and Clarifications

A. Does Constant Velocity Mean No Friction?
No, constant velocity does not mean there is no friction. Even when an object is moving at a constant velocity, it can still experience a frictional force. However, since the object’s velocity is constant, the frictional force is balanced by other forces acting on the object, resulting in a net force of zero. This means that the object continues to move at a constant velocity, overcoming the frictional force.
B. Is There Friction with Constant Velocity?
Yes, there can be friction with constant velocity. friction always exists between two surfaces in contact, regardless of whether the object is at rest, in motion, or moving at a constant velocity. The frictional force opposes the object’s motion and can affect its velocity. However, when the object reaches a constant velocity, the frictional force is balanced by other forces, resulting in no change in velocity over time.
C. Clarifying the Misconceptions
To clarify, constant velocity does not mean there is no friction or that friction disappears. friction is always present between surfaces in contact, even when an object is moving at a constant velocity. However, when an object reaches a constant velocity, it means that the frictional force is balanced by other forces, allowing the object to maintain a steady speed. This balance of forces ensures that the object’s velocity remains unchanged over time.
Understanding how to calculate constant velocity with friction is crucial for analyzing the motion of objects in the presence of frictional forces. By considering the role of friction force, the importance of the coefficient of friction, and following the steps outlined, we can accurately determine the constant velocity of an object in the presence of friction. Remember that even when an object is moving at a constant velocity, friction is still at play, and it’s essential to consider its effects. So, next time you encounter a situation involving constant velocity with friction, you’ll be well-equipped to tackle it confidently!
Also Read:
- How to calculate drift velocity in semiconductors
- How to find average velocity on a acceleration time graph
- Constant acceleration graph velocity vs time
- Rpm to angular velocity
- Velocity vs acceleration graph
- Negative velocity positive acceleration graph
- Velocity
- How to determine velocity in space time curvature
- How to find velocity using huygens principle
- Can velocity be negative













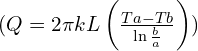 , where ( Q ) represents the heat transfer rate.
, where ( Q ) represents the heat transfer rate.