Points of Discussions: AC Circuit Analysis
Introduction to Advanced AC Circuit Analysis
In the previous article of the AC circuit, we have discussed some of the basic ac circuit analysis. We have studied about the circuit, the phasor diagrams, power calculations, and some essential terminologies. In this article, we will learn some advanced AC circuit analysis like – RC Series circuit, RL series circuit, RLC series circuit, etc. These advanced circuits are essential and have more applications in electrical analysis. All of these circuits can be said another level of primary ac circuit as the more complex circuit can be built using these. Please check out the introductory circuit article before studying this advanced ac circuit analysis.
Basic AC Circuit Analysis: Read Here!
RC Series Circuit
If a pure resistor is placed in a series with a pure capacitor in an AC circuit, then the ac circuit will be called RC AC Series Circuit. An ac voltage source produces sinusoidal voltages and the current passes through the resistor and the capacitor of the circuit.
- Circuit diagram of RC series circuit
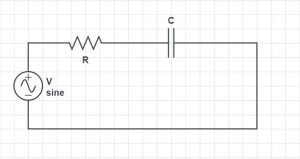
VR gives the voltage across the resistance, and – VC gives the voltage across the capacitor. The current through the circuit is I. R is the resistance and C is the capacitance value. XC denotes the capacitive reactance of the capacitor.
- Phasor diagram of RC series circuit
The process to draw the phasor diagram of RC Circuit.
The phasor diagram is an essential analytical tool which helps to study the behaviour of the circuit. Let us learn the steps to draw the phasor.
Step 1. Find out the r.m.s value of the current. Mark that as the reference vector.
Step 2. As we know that for a purely resistive circuit, voltage and current remains in the same phase, here as well voltage drop across the resistor stays in phase with the current value. It is given as V = IR.
Step 3. Now for the capacitive circuit, we know that voltage lags by 90 degrees and current leads. That is why voltage drop across the capacitor in this circuit, stays 90 degrees behind than the current vector.
Step 4. The applied voltage thus comes as the vector sum of the voltage drops of capacitor and resistances. So, it can be written as:
V2 = VR2 + VC2
Or, V2 = (IR)2 + (IXC)2
Or, V = I √ (R2 + XC2)
Or, I = V / √ (R2 + XC2)
Or, I = V / Z
Z is the aggregate impedance of the RC circuit. The following equation represents the mathematical form.
Z = √ (R2 + XC2)
Now from the phasor diagram, we can observe there is an angle as – ϕ.
So, tan ϕ will be equal to IXC / IR.
So, ϕ = tan-1 (IXC / IR)
This angle ϕ is known as phase angle.
- RC Series Circuit Power calculation
The power of the circuit is calculated by P = VI formula. Here we will calculate the instantaneous value of power.
So, P = VI
Or, P = (Vm Sinωt) * [Im Sin (ωt+ ϕ)]
Or, P = (Vm Im / 2) [ 2Sinωt * Sin (ωt+ ϕ)]
Or, P = (Vm Im / 2) [ cos {ωt – (ωt+ ϕ)} – cos {ωt – (ωt+ ϕ)}]
Or, P = (Vm Im / 2) [ cos (- ϕ) – cos (2ωt+ ϕ)]
Or, P = (Vm Im / 2) [ cos (ϕ) – cos (2ωt+ ϕ)]
Or, P = (Vm Im / 2) cos (ϕ) – (Vm Im / 2) cos (2ωt+ ϕ)
We can observe that the power equation has two sections. One is a constant part another is the variable section. The mean of the variable part comes to be zero over a full cycle.
So, the average power for an RC series circuit, over a full cycle is given as :
P = (Vm Im / 2) cos (ϕ)
Or, P = (Vm / √2) * (Im / √2) * cos (ϕ)
Or, P = VI cos (ϕ)
Here, V and I are considered as RMS values.
The power factor of RC Series Circuit
The RC series circuit’s power factor is given by the ratio of active power to the apparent power. It is represented by cosϕ and expressed as below given expression.
cos ϕ = P / S = R / √ (R2 + XC2)
RL Series Circuit
If a pure resistor is placed in a series with a pure inductor in an AC circuit, then the ac circuit will be called RL AC Series Circuit. An ac voltage source produces sinusoidal voltages and the current passes through the resistor and the inductor of the circuit.
- Circuit Diagram of RL circuit
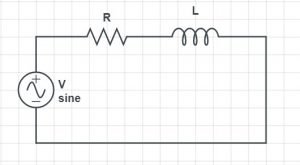
VR gives the voltage across the resistance, and – VL gives the voltage across the inductor. The current through the circuit is I. R is the resistance and L is the inductance value. XL denotes the inductive reactance of the inductor.
- Phasor Diagram of RL circuit
The process to draw the phasor diagram of RL Circuit.
Step 1. Find out the r.m.s value of the current. Mark that as the reference vector.
Step 2. As we know, for a purely resistive circuit, voltage and current remain in the same phase, here as well voltage drop across the resistor stays in phase with the current value. It is given as V = IR.
Step 3. Now for the inductive circuit, we know that voltage leads by 90 degrees and the current lags. That is why voltage drop across the inductor in this circuit, stays 90 degrees ahead than the current vector.
Step 4. The applied voltage comes as the vector sum of the voltage drops of inductor and resistances. So, it can be written as:
V2 = VR2 + VL2
Or, V2 = (IR)2 + (IXL)2
Or, V = I √ (R2 + XL2)
Or, I = V / √ (R2 + XL2)
Or, I = V / Z
Z is the aggregate impedance of the RL circuit. The following equation represents the mathematical form.
Z = √ (R2 + XL2)
Now from the phasor diagram, we can observe there is an angle as – ϕ.
So, tan ϕ will be equal to IXL / IR.
So, ϕ = tan-1 (XL / R)
This angle ϕ is known as phase angle.
- RL Series Circuit Power calculation
The power of the circuit is calculated by P = VI formula. Here we will calculate the instantaneous value of power.
So, P = VI
Or, P = (Vm Sinωt) * [Im Sin (ωt- ϕ)]
Or, P = (Vm Im / 2) [ 2Sinωt * Sin (ωt – ϕ)]
Or, P = (Vm Im / 2) [ cos {ωt – (ωt – ϕ)} – cos {ωt – (ωt – ϕ)}]
Or, P = (Vm Im / 2) [ cos (ϕ) – cos (2ωt – ϕ)]
Or, P = (Vm Im / 2) cos (ϕ) – (Vm Im / 2) cos (2ωt – ϕ)
We can observe that the power equation has two sections. One is a constant part another is the variable section. The mean of the variable part comes to be zero over a full cycle.
So, the average power for an RL series circuit, over a full cycle is given as :
P = (Vm Im / 2) cos (ϕ)
Or, P = (Vm / √2) * (Im / √2) * cos (ϕ)
Or, P = VI cos (ϕ)
Here, V and I are considered as RMS values.
LC Series Circuit
An LC series circuit is an AC circuit consisting of inductor and capacitor, placed in a series connection. An LC circuit has several applications. It is also known as a resonant circuit, tuned circuit, LC filters. As there is no resistor in the circuit, ideally this circuit doesn’t suffer any losses.
LC Circuit as Tuned Circuit: The flow of current means flows of charges. Now in an LC circuit, charges keep flowing behind and ahead of the capacitor plates and through the inductor. Thus, a type of oscillation gets created. That is why these circuits are known as tuned or tank circuit. However, the internal resistance of the circuit prevents the oscillation in real.
- Circuit diagram of LC Series Circuit
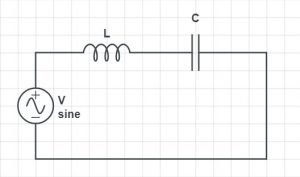
In a series circuit, the current value is the same across the whole circuit. So we can write that, I = IL = IC.
The voltage can be written as V = VC + VL.
- Resonance in series LC Circuit
Resonance is refereed to as a particular condition of this LC circuit. If the frequency of the current increases, the value of inductive reactance also gets increased, and the value of capacitive reactance gets decreased.
XL = ωL = 2πfL
XC = 1 / ωC = 2πfC
At the resonance condition, the magnitude of capacitive reactance and inductive reactance is equal. So, we can write that XL = XC
Or, ωL = 1 / ωC
Or, ω2C = 1 / LC
Or, ω = ω0 = 1 / √LC
Or, 2πf = ω0 = 1 / √LC
Or, f0 = ω0 / 2π = (1/2π) (1 / √LC)
f0 is the resonant frequency.
- The impedance of the circuit
Z = ZL + ZC
Or, Z = jωL + 1 / jωC
Or, Z = jωL + j / j2ωC
Or, Z = jωL – j / ωC

Hi, I am Sudipta Roy. I have done B. Tech in Electronics. I am an electronics enthusiast and am currently devoted to the field of Electronics and Communications. I have a keen interest in exploring modern technologies such as AI & Machine Learning. My writings are devoted to providing accurate and updated data to all learners. Helping someone in gaining knowledge gives me immense pleasure.
Let’s connect through LinkedIn –