The article discusses about what is speed of a transverse wave with some solved problems and examples.
The particles within the transverse wave move perpendicular to wave propagating. When the wave moves, its particles oscillate from their equilibrium position, which we call the ‘speed of a transverse wave’. It depends on the wavelength and frequency properties of the transverse wave.
The particles oscillation from equilibrium or mean position sets up the properties of the transverse, and it is measured as the particle’s ‘displacement’ (s). The maximum displacement from their mean position gives rise to its ‘Amplitude‘ (denoted as A).
The peaks emerge above the mean position due to maximum displacement called ‘crest’, whereas the peaks emerge lower than the mean position due to maximum displacement called ‘trough’. The shape of the crest and trough is a natural process when transverse waves propagate.
So when we estimate the horizontal distance the transverse wave travels, we get another wave property called ‘Wavelength’, denoted by symbol lambda (λ). It is the distance between either two crests or two troughs; hence it is measured in a metre (m).
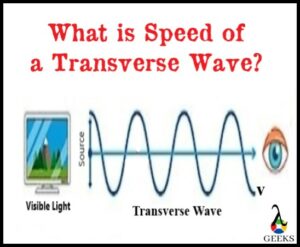
The time is taken by an entire wavelength or two successive crests to pass through a fixed point called ‘Period’ (denoted as T). Whereas the number of wavelengths travelling in one second through a given point is called ‘Frequency’ (denoted as f), and it has a measuring unit as Hertz (denoted by Hz).

(credit: shutterstock)
Speed of a Transverse Wave Formula
The speed of a transverse wave is obtained from its properties like wavelength, frequency and period.
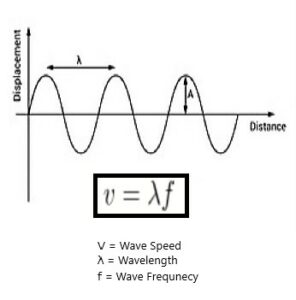
The distance travelled by a transverse wave in unit time describes its speed. Hence, the distance between two crests or troughs in the transverse wave is calculated as one wavelength, whereas the unit time is one period. Therefore, the speed of the transverse wave formula is the ratio of its wavelength to period.
Math
v = λ/t ……………..(*)
But as per definitions, the period (T) and frequency (f) are reciprocal. i.e., f = 1/T
Equation (*) becomes,
v = λ/T
The speed of a transverse wave formula is,
v = λ/f
(credit: shutterstock)
What is the speed of a transverse wave, which has a wavelength of 50m and a frequency of 100Hz?
Given:
λ = 50m
f = 100Hz
To Find:
v =?
Formula:
v = λ/f
Solution:
The speed of a transverse wave is calculating as,
v = λ/f
Substituting all values,
v = 50 x 100
v = 500
The speed of a transverse wave is 500m/s.
If the sound wave has a frequency of 200Hz, what is its time period to pass successive wave crests? Also, calculate the speed of a sound wave if its wavelength is 80m.
Given:
f = 200Hz
λ = 80m
To Find:
T =?
v =?
Formula:
f =1/T
v = λ/f
Solution:
The time period of sound wave is calculated as,
f = 1/T
T= 1/f
Substituting values,
T= 1/200
T = 5 x 10-3
T = 5ms
The time period of a transverse sound wave is 5ms.
The speed of a transverse wave is calculating as,
v =λf
Substituting all values,
v = 80 x 200
v = 1600
The speed of a sound waves is 1600m/s.
When the guitar string is plucked, it produces transverse waves. If the waves having a wavelength of 40m moves at 200m/s, what is the time period of waves?
Given:
λ = 40m
v = 200m/s
To Find:
T =?
Formula:
v = λf
f= 1/T
Solution:
First we calculate the frequency of transverse of wave as,
v = λf
f = v/λ
Substituting all values,
f = 200/40
f = 50
The frequency of the transverse wave produced on the guitar string is 50Hz.
The time period of transverse wave is calculated as,
T= 1/f
T= 1/50
T = 20 x 10-3
The time period of a transverse wave is 20ms.
Read more about How to Calculate Speed.
What is the Speed of a Transverse Wave on a Stretched String?
The speed of a transverse wave generated on a stretched string is the ratio of its tension and linear density quantities.
When we pluck the stretched string tied at both ends, it vibrates to create the number of sound waves as transverse waves. The sound waves move with higher speed on a stretched strings than other mediums because of the string’s high tension values and low mass per unit length.
The string is one of the flexible connectors that transmit the disturbance to both ends when stretched. The disturbance is reflected from both ends and creates sound waves on the string. Tension (denoted as T) is the main kay that makes the disturbance travel throughout the string. It is one of the types of force that transmits the applied force and prevents the flexible connector from breaking.
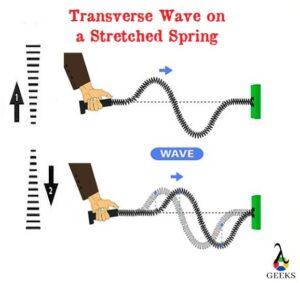
Even though string has different thicknesses, it is made of the same material. Its mass per unit length is what we termed as linear density (denoted as μ). So,
mu =m/I
Instead of its frequency, the speed of a transverse wave created on a stretched string depends on its tension and linear density.
“The transverse wave speed is directly proportional to the square root of tension (T) and inversely proportional to the square root of the linear density μ.”
v = √T/mu
The rope is also one of the flexible connectors like a string. Hence, the speed of a transverse wave formula for the rope is the same as for the stretched string.

(credit: shutterstock)
Read more about Tension in Flexible Connectors.
What is the speed of a transverse wave on a stretched string with a tension of 300N and a linear density of 0.15kg/m?
Given:
T = 300N
μ = 0.15kg/m
To Find:
v =?
Formula:
v = √T/mu
Solution:
The speed of a transverse wave is,
v = √T/mu
Substituting all values,
v =√300/0.15
v = √2000
v = 44.72
The speed of a transverse wave is 44.72m/s.
A guitar string has a mass of 2kg and 10m. What should be the tension on the string so that the speed of a sound waves equals 300m/s.
Given:
m = 2kg
l = 10m
v = 300m/s
To Find:
T =?
Formula:
v = √T/mu
Solution:
First we need to calculate the linear density as,
mu = m/I
Substituting all values,
mu = 2/10
mu = 0.2kg/m
The tension on string is calculated as,
v = √T/mu
Squaring both sides,
v2 = T/mu
T = v2mu
Substituting all values,
T = 3002 x 0.2
T = 900 x 0.2
T = 180
The tension on the string is 180N.
What is the tension on the rope of 5kg and 8m long on which the produced transverse wave travels 20m in 5s?
Given:
m = 5kg
l = 8m
d = 20m
t = 5s
To Find:
T =?
Formula:
v = √T/mu
Solution:
First we need to calculate the linear density as,
mu = m/I
Substituting all values,
mu = 5/8
mu = 0.62
The tension on the rope is calculated as,
v = √T/mu
But speed formula is v= d/t, hence
Squaring both sides,
20/5 = √T/0.62
4 = √T/0.62
Squaring both sides,
16 = √T/0.62
T = 16 x 0.62
T = 9.92
The tension on the rope is 9.92N.
Read more about How to Calculate Mass.
Do all Transverse Waves have Same Speed?
All transverse waves have the same speed in vacuum only, not in medium.
Electromagnetic (EM) waves are transverse waves that move at the same vacuum speed, i.e., 3×108m/s. But when it passes through any medium, its speed decreases as a wave-particle interacts with particles of the medium.
The permittivity or permeability quantity of the medium affects the constant speed of a transverse waves. Although the wave’s frequency stays intact in the medium, its wavelength varies slightly. That’s the reason when the white light passes through a dispersed medium like a prism; it splits into different colors as its speed changes into the prism.
“The amount of change in speed of a transverse waves is given by the formula of the index of refraction (n) as waves get refracted into the medium.”
(credit: shutterstock)
n = c/v
where c is the light speed in a vacuum.
v is the light speed in the medium.
Read more about Speed Vs. Velocity.
What is the speed of a transverse wave in glass with the index of refraction as 1.5?
Given:
n = 1.5
c = 3×108m/s
To Find:
v =?
Formula:
n = c/v
Solution:
The speed of a transverse wave in a glass is calculated as,
n = c/v
v = 3.8 x 108/1.5
v = 2.53 x 108
The speed of a transverse wave in the glass is 2.53 x 108m/s.
Also Read:
- Electromagnetic waves examples
- Telescope in gravitational wave research
- Can longitudinal waves travel through a vacuum
- Why does energy exhibit wave particle duality
- How to find frequency of transverse wave
- Does amplitude increase in a wave
- Longitudinal wave example
- How to find energy with given wavelength
- Does wavelength affect diffraction
- How did the concept of wave particle duality come about

Hello, I’m Manish Naik completed my MSc Physics with Solid-State Electronics as a specialization. I have three years of experience in Article Writing on Physics subject. Writing, which aimed to provide accurate information to all readers, from beginners and experts.
In my leisure time, I love to spend my time in nature or visiting historical places.
Looking forward to connecting you through LinkedIn –