Velocity - lambdageeks.com

The Velocity Formula: A Comprehensive Guide for Physics Students

June 25, 2024March 4, 2022 by Core SME lambdageeks.com

The velocity formula is a fundamental concept in physics that measures the rate of change of an object’s position with respect to time. This comprehensive guide will provide you with a deep understanding of the velocity formula, its applications, and practical examples to help you master this essential topic. Definition and Formula Velocity is defined … Read more

Discover How to Find Velocity with Force: A Comprehensive Guide for Physics Students

June 25, 2024March 1, 2022 by Core SME lambdageeks.com

Summary Discovering how to find velocity with force is a fundamental concept in physics that is crucial for understanding the motion of objects. This comprehensive guide will provide you with a deep dive into the various formulas, principles, and examples related to calculating velocity using force. From understanding the relationship between force and stretch to … Read more

How To Find Constant Velocity: Different Approaches And Problem Examples

January 21, 2024February 28, 2022 by Abhishek

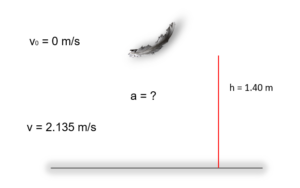
Constant velocity refers to the motion of an object where its speed remains unchanged and its direction of motion remains constant over time. It is an essential concept in physics and is often used to analyze various kinds of motion, such as linear motion or motion along a curve. In this blog post, we will explore how to find constant velocity, the factors that influence it, and its practical applications.

How to Calculate Constant Velocity

how to find constant velocity — Image by en:User:Anrp – Wikimedia Commons, Wikimedia Commons, Licensed under CC BY 2.5.

The Equation for Constant Velocity

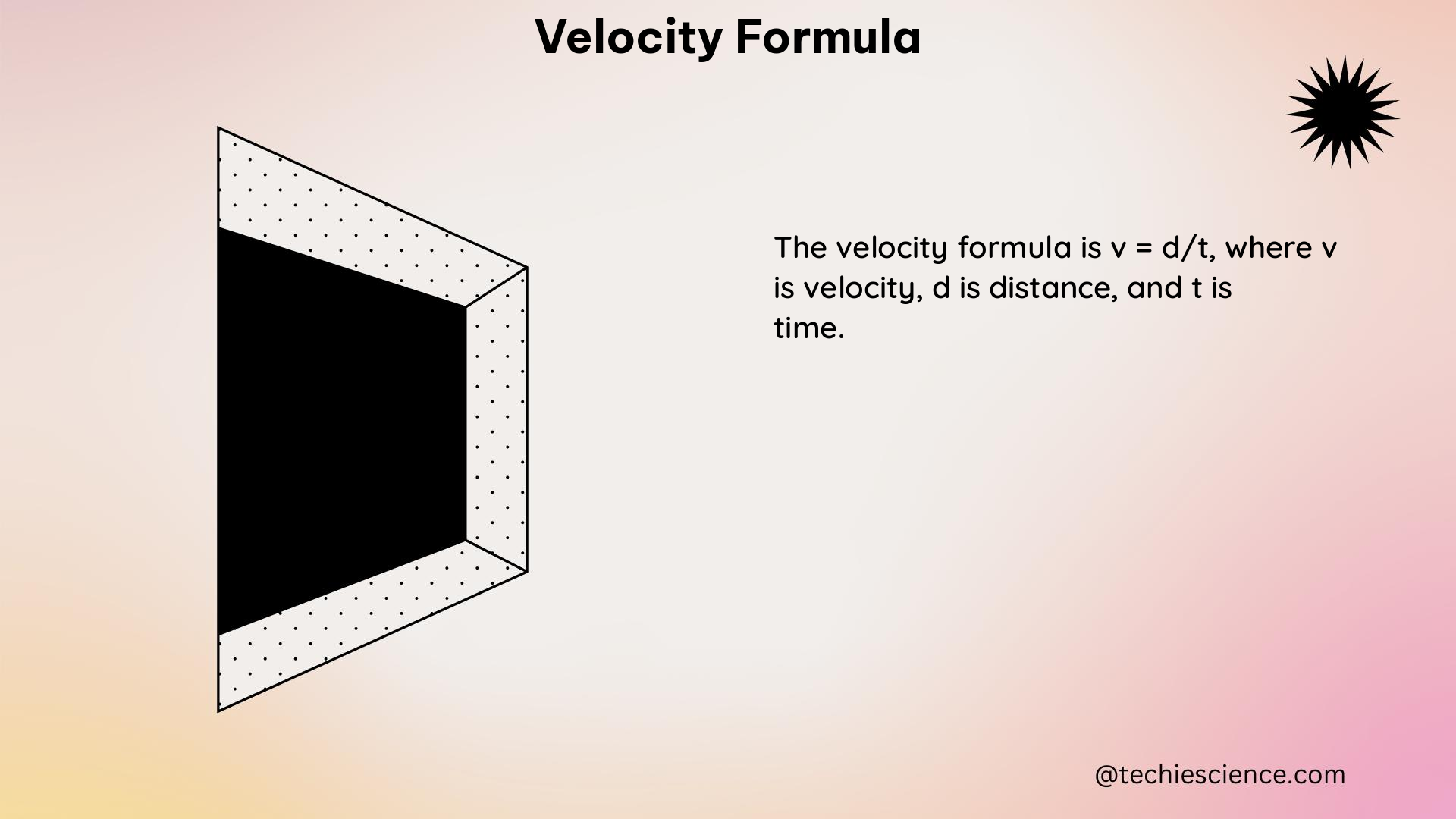
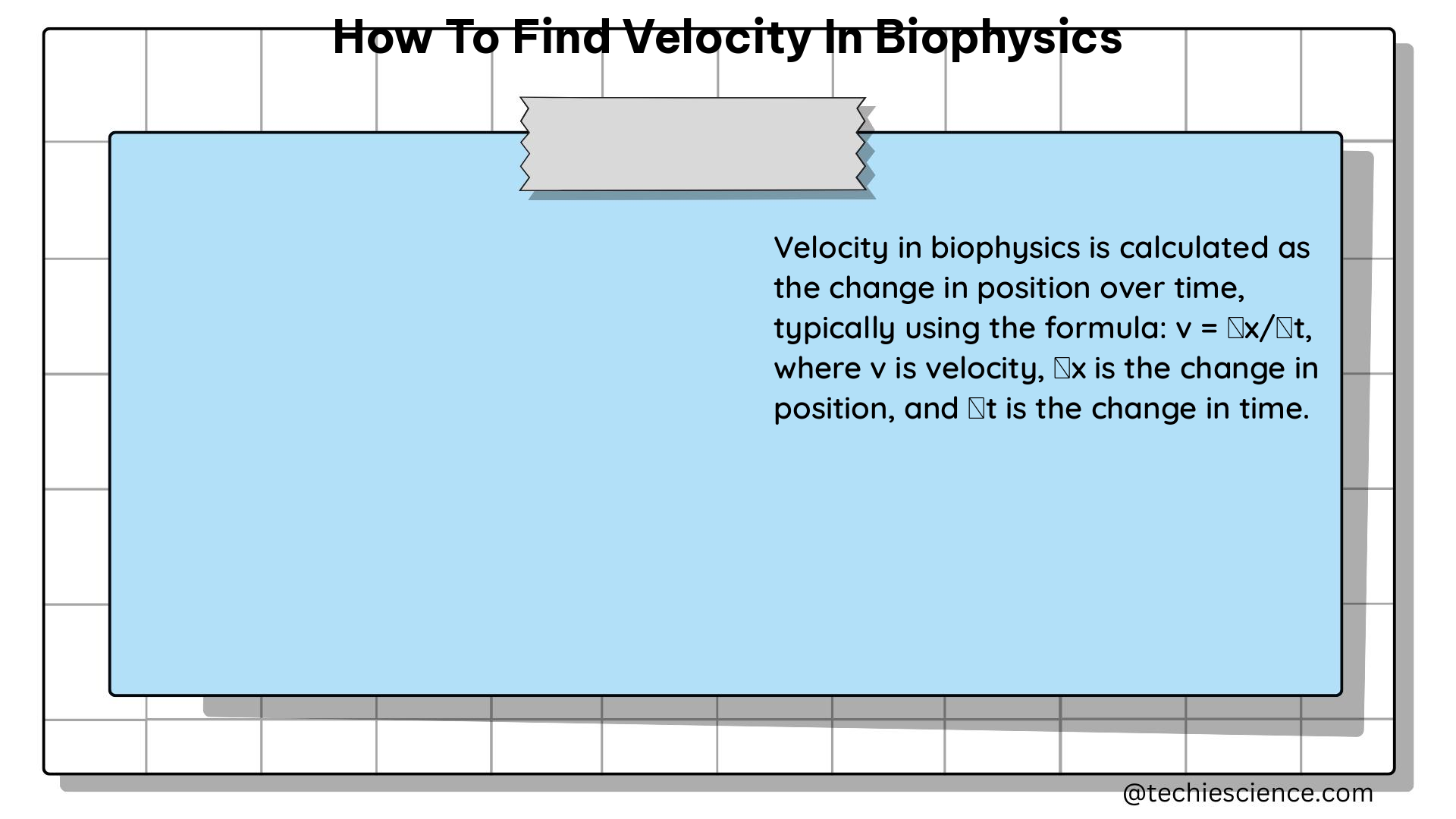
To calculate constant velocity, we use the equation:

$\text{Constant Velocity (v)} = \frac{\text{Change in Position (Δx)}}{\text{Change in Time (Δt)}}$

This equation states that the constant velocity is equal to the change in position divided by the change in time. It provides a straightforward way to determine the velocity of an object when its speed remains constant.

How to Use the Constant Velocity Formula

Let’s break down the steps involved in using the constant velocity formula:

Determine the initial and final positions of the object.
Calculate the change in position (Δx) by subtracting the initial position from the final position.
Determine the time elapsed between the initial and final positions.
Calculate the change in time (Δt) by subtracting the initial time from the final time.
Substitute the values of Δx and Δt into the constant velocity formula to find the velocity.

Worked Out Examples on Calculating Constant Velocity

Now, let’s work through a couple of examples to solidify our understanding of constant velocity calculations.

Example 1:

Suppose a car travels 100 meters in 20 seconds along a straight road. What is its constant velocity?

Given:
Initial position (x1) = 0 meters
Final position (x2) = 100 meters
Initial time (t1) = 0 seconds
Final time (t2) = 20 seconds

Using the formula, we can calculate the constant velocity:

$\text{Constant Velocity (v)} = \frac{\text{Change in Position (Δx)}}{\text{Change in Time (Δt)}}$

$v = \frac{100 \, \text{m} - 0 \, \text{m}}{20 \, \text{s} - 0 \, \text{s}} = \frac{100 \, \text{m}}{20 \, \text{s}} = 5 \, \text{m/s}$

Therefore, the car’s constant velocity is 5 meters per second.

Example 2:

Suppose a person walks a total distance of 1200 meters in 10 minutes. What is their constant velocity?

Given:
Initial position (x1) = 0 meters
Final position (x2) = 1200 meters
Initial time (t1) = 0 minutes
Final time (t2) = 10 minutes

Converting minutes to seconds:
Initial time (t1) = 0 minutes × 60 seconds/minute = 0 seconds
Final time (t2) = 10 minutes × 60 seconds/minute = 600 seconds

Using the formula, we can calculate the constant velocity:

$v = \frac{1200 \, \text{m}}{600 \, \text{s}} = 2 \, \text{m/s}$

Therefore, the person’s constant velocity is 2 meters per second.

Factors Influencing Constant Velocity

Role of Acceleration in Constant Velocity

In the context of constant velocity, it is important to note that acceleration is zero. Acceleration is defined as the rate of change of velocity with respect to time. Since constant velocity implies a constant speed, there is no change in velocity over time, resulting in zero acceleration.

Impact of Friction on Constant Velocity

Friction plays a crucial role in determining the constant velocity of an object. In the absence of external forces, such as friction, an object in motion will continue to move at a constant velocity. However, when friction is present, it opposes the motion of the object, potentially causing a decrease in velocity. In some cases, the force of friction can balance with other forces, resulting in a constant velocity despite its presence.

How Distance and Time Affect Constant Velocity

The concept of constant velocity heavily relies on the relationship between distance and time. If an object covers the same distance in the same amount of time, it indicates a constant velocity. However, any changes in distance or time can lead to a change in velocity. Therefore, it is important to analyze changes in these factors when considering constant velocity.

Practical Applications of Constant Velocity

Checking Constant Velocity Joint

Constant velocity (CV) joints are commonly used in vehicles to transmit torque smoothly while allowing for a range of motion. The ability to maintain constant velocity is crucial for smooth and efficient operation. By checking the velocity of the CV joint, mechanics can ensure that it is functioning properly and not causing any issues, such as vibrations or jolts during acceleration.

Finding Constant Velocity in Physics

In physics, constant velocity is often used to analyze the motion of objects in various scenarios. By determining the constant velocity of an object, physicists can make predictions about its future behavior and understand the underlying principles governing the motion.

Using Constant Velocity in Real-World Scenarios

Constant velocity has practical applications in many real-world scenarios. For example, in sports such as athletics or swimming, measuring the constant velocity of an athlete can provide insights into their performance and potential improvements. Additionally, in transportation and logistics, understanding the constant velocity of vehicles can help optimize routes and improve efficiency.

These are just a few examples of how constant velocity is applied in different fields, highlighting its significance in various aspects of our lives.

By understanding how to find constant velocity, the factors that influence it, and its practical applications, we can gain a deeper insight into the world of motion and its implications across different disciplines.

Remember, constant velocity is not just a mathematical concept, but a fundamental aspect of how objects move and interact in the world around us.

Numerical Problems on how to find constant velocity

Problem 1:

A car travels a distance of 200 meters in 10 seconds. Determine its constant velocity.

Solution:

Given:
Distance, $d = 200 \, \text{m}$
Time, $t = 10 \, \text{s}$

We know that velocity $\(v$ ) is given by the formula:

$v = \frac{d}{t}$

Substituting the given values, we get:

$v = \frac{200}{10}$

Hence, the constant velocity of the car is 20 m/s.

Problem 2:

A cyclist covers a distance of 5 kilometers in 30 minutes. Find the constant velocity of the cyclist.

Solution:

Given:
Distance, $d = 5 \, \text{km}$
Time, $t = 30 \, \text{min}$

First, we need to convert the time from minutes to hours. Since 1 hour equals 60 minutes, we have:

$t = \frac{30}{60} = \frac{1}{2} \, \text{hour}$

Now, we can calculate the constant velocity using the formula:

$v = \frac{d}{t}$

Substituting the given values, we get:

$v = \frac{5}{\frac{1}{2}}$

Simplifying, we get:

$v = 10 \, \text{km/h}$

Therefore, the constant velocity of the cyclist is 10 km/h.

Problem 3:

A train covers a distance of 500 miles in 5 hours. Determine its constant velocity.

Solution:

Given:
Distance, $d = 500 \, \text{miles}$
Time, $t = 5 \, \text{hours}$

We can calculate the constant velocity using the formula:

$v = \frac{d}{t}$

Substituting the given values, we get:

$v = \frac{500}{5}$

Simplifying, we get:

$v = 100 \, \text{miles/hour}$

Hence, the constant velocity of the train is 100 miles/hour.

Also Read:

The Escape Velocity of Earth: A Comprehensive Guide

June 25, 2024February 26, 2022 by Core SME lambdageeks.com

The escape velocity of Earth is the minimum speed required for an object to overcome the planet’s gravitational pull and escape its gravitational influence. This critical velocity is a fundamental concept in astrophysics and space exploration, as it determines the feasibility of launching spacecraft and satellites into orbit or beyond Earth’s atmosphere. In this comprehensive … Read more

Is Angular Velocity Constant?

June 25, 2024February 25, 2022 by Abhishek

Angular velocity is a fundamental concept in physics that describes the rate of change of an object’s angular displacement. The question of whether angular velocity is constant depends on the specific context and the motion being studied.

Uniform Circular Motion

In uniform circular motion, the angular velocity is constant. This means that the object moves in a circle at a constant speed, and the angular displacement changes at a constant rate. The angular velocity (ω) is defined as the rate of change of the angular displacement (θ) with respect to time (t):

\omega = \frac{\text{d}\theta}{\text{d}t}

For uniform circular motion, ω is constant, which implies that the angular displacement changes at a constant rate over time.

Examples of Uniform Circular Motion

Spinning Top: A spinning top maintains a constant angular velocity as it rotates around its central axis.
Ferris Wheel: The angular velocity of a Ferris wheel is constant, as each passenger car completes one full revolution in the same amount of time.
Centrifuge: In a centrifuge, the samples rotate at a constant angular velocity, which is crucial for separating substances based on their density.

Formulas and Calculations

The constant angular velocity (ω) in uniform circular motion can be used to calculate other important quantities:

Angular Displacement (θ): θ = ω * t
Tangential Velocity (v): v = ω * r, where r is the radius of the circular path.
Centripetal Acceleration (a): a = ω^2 * r

For example, if a Ferris wheel has an angular velocity of 0.2 rad/s and a radius of 20 meters, the tangential velocity of a passenger car would be:

v = ω * r
v = 0.2 rad/s * 20 m
v = 4 m/s

Angular Velocity in Rotating Systems

In rotating systems, such as a spinning disk or the Earth’s atmosphere, the angular velocity can also be constant. This means that all points on the rotating body have the same angular velocity, regardless of their radial distance from the center of rotation. The angular velocity is a property of the body or the reference frame and does not depend on the location where it is measured.

Examples of Constant Angular Velocity in Rotating Systems

Earth’s Atmosphere: The atmosphere rotates with the same angular velocity as the Earth, which is approximately 15 degrees per hour or 7.27 × 10^(-5) rad/s.
Spinning Disk: The angular velocity of a spinning disk remains constant for all points on the disk, regardless of their radial distance from the center. This is because every point on the disk completes one full revolution in the same amount of time.
Rotating Machinery: In industrial machinery, such as turbines and generators, the rotating components often maintain a constant angular velocity to ensure efficient and stable operation.

Theoretical Explanation

The constancy of angular velocity in rotating systems can be explained by the definition of angular velocity as the rate of change of angular displacement. Since all points on the rotating body complete one full revolution in the same amount of time, their angular velocity remains constant. This is in contrast to tangential velocity, which varies with radial distance due to the increasing circumference of the circle at greater distances from the center.

Formulas and Calculations

The key formulas and theorems related to constant angular velocity in rotating systems are:

Angular Velocity: ω = dθ/dt
Tangential Velocity: v = ω * r
Angular Displacement: θ = Δs/r

For example, if a spinning disk has an angular velocity of 10 rad/s and a radius of 0.5 meters, the tangential velocity of a point on the disk’s edge would be:

v = ω * r
v = 10 rad/s * 0.5 m
v = 5 m/s

Numerical Problems and Data Points

Spinning Top: A spinning top has an initial angular velocity of 50 rad/s. If the top maintains a constant angular velocity, calculate the angular displacement after 10 seconds.

“`
Given:
Initial angular velocity (ω) = 50 rad/s
Time (t) = 10 s

Angular displacement (θ) = ω * t
θ = 50 rad/s * 10 s
θ = 500 rad
“`

Ferris Wheel: A Ferris wheel has a radius of 20 meters and a constant angular velocity of 0.2 rad/s. Calculate the tangential velocity of a passenger car at the top of the wheel.

“`
Given:
Radius (r) = 20 m
Angular velocity (ω) = 0.2 rad/s

Tangential velocity (v) = ω * r
v = 0.2 rad/s * 20 m
v = 4 m/s
“`

Earth’s Atmosphere: The Earth’s atmosphere rotates with a constant angular velocity of 7.27 × 10^(-5) rad/s. Calculate the time it takes for the atmosphere to complete one full revolution around the Earth.

“`
Given:
Angular velocity (ω) = 7.27 × 10^(-5) rad/s

Time for one full revolution (T) = 2π / ω
T = 2π / (7.27 × 10^(-5) rad/s)
T = 24 hours
“`

Spinning Disk: A spinning disk has a radius of 0.5 meters and a constant angular velocity of 10 rad/s. Calculate the centripetal acceleration of a point on the disk’s edge.

“`
Given:
Radius (r) = 0.5 m
Angular velocity (ω) = 10 rad/s

Centripetal acceleration (a) = ω^2 * r
a = (10 rad/s)^2 * 0.5 m
a = 50 m/s^2
“`

These examples demonstrate the application of the formulas and theorems related to constant angular velocity in both uniform circular motion and rotating systems.

Conclusion

In summary, angular velocity can be constant in two main scenarios:

Uniform Circular Motion: In uniform circular motion, the angular velocity is constant, meaning the object moves in a circle at a constant speed, and the angular displacement changes at a constant rate.
Rotating Systems: In rotating systems, such as a spinning disk or the Earth’s atmosphere, the angular velocity can also be constant, with all points on the rotating body having the same angular velocity, regardless of their radial distance from the center of rotation.

The constancy of angular velocity in these cases can be explained by the definition of angular velocity as the rate of change of angular displacement. Understanding the concept of constant angular velocity is crucial in various fields of physics, engineering, and astronomy, as it underpins the analysis and design of many rotating systems and mechanisms.

References

Biomechanics of Human Movement. (n.d.). Retrieved from https://pressbooks.bccampus.ca/humanbiomechanics/chapter/6-1-rotation-angle-and-angular-velocity-2/
Constant Angular Velocity. (n.d.). Retrieved from https://www.sciencedirect.com/topics/engineering/constant-angular-velocity
Constant Angular Velocity. (n.d.). Retrieved from https://www.sciencedirect.com/topics/computer-science/constant-angular-velocity
Why Does the Atmosphere Rotate with Constant Angular Velocity?. (2016, June 18). Retrieved from https://www.physicsforums.com/threads/why-does-atmosphere-rotate-w-constant-angular-velocity.875999/
Why Is Angular Velocity the Same for All Points on a Spinning Disk?. (2020, May 2). Retrieved from https://physics.stackexchange.com/questions/548631/why-is-angular-velocity-the-same-for-all-points-on-a-spinning-disk-even-though

How to Compute Velocity in Neutron Stars: A Comprehensive Guide

June 25, 2024February 23, 2022 by Core SME lambdageeks.com

Neutron stars are the ultra-dense remnants of massive stars that have undergone gravitational collapse, making them fascinating objects to study. Determining the velocity of these celestial bodies is crucial for understanding their dynamics, evolution, and interactions with the surrounding environment. In this comprehensive guide, we will delve into the various methods and models used to … Read more

Drag Coefficient And Velocity: Relation,Different Aspects And Facts

January 21, 2024February 20, 2022 by Keerthi Murthi

The drag is a force associated with the object in motion in a fluid environment. Drag force is specified by a dimensionless entity called drag coefficient, which helps describe the nature of the motion in the fluid.

The drag coefficient always defines the resistance offered to the object under motion in a fluid. Since the object under motion possesses a certain velocity, the drag coefficient and velocity are related. This post briefly explains the relationship between drag coefficient and velocity in various aspects.

Relation between drag coefficient and velocity

Drag coefficient C_D is always defined using the terms such as density of the fluid, reference area of cross-section of the object, velocity, and the Reynolds number; thus, the relation between the drag coefficient and velocity can be written using the equation.

C_D=2F_D/v²Aρ

Where FD is the drag force, ρ is the mass density of the fluid; A is the reference area, and v is the relative velocity of the object in the fluid.

From the above expression, the relation between the drag coefficient CD and relative velocity v is given as

C_D∝ 1/v²

The above expression means that a square increase in velocity decreases the drag coefficient. Thus drag coefficient and velocity are inversely related to each other.

Drag force and velocity relationship

The drag force always retards the flow of the object in the fluid. As the velocity increases, the drag force associated with it changes proportionally. The drag force acting on the object in a fluid is given by

F_D=1/2 C_Dv²Aρ

From the above equation, in fluid mechanics, the relation between drag and velocity is explained by considering the object’s speed as low and high speed. The drag force varies differently for low and high speeds.

For low-speed flow, the drag force is proportional to the velocity given by

F_D∝ v

For high-speed flow, the drag force is proportional to the square of the velocity given as

F_D∝ v²

How does velocity affect drag?

The dependency of the drag on the square of the velocity is quite natural in the fluid dynamics, as the velocity shows some deviation in the drag when it changes.

The object floating in the fluid is associated with doubling velocity –this means as the velocity is increased to its square value, the drag increases by quadruple. The quadruple increase in the drag is due to other entities associated with the drag. The effect of velocity on drag is given by

D∝ v²

Thus we can write the above proportionality as

D=constant×v²

The constant in the above expression is regarded with the density, area, and drag coefficient associated with the drag.

Thus as the relative velocity increases to its square value, the drag increases by four times.

Drag force and angular velocity

Angular velocity is always associated with the rotating motion of the object. In order to describe drag force with the angular velocity, we have to consider linear drag expression; it is given below:

F_D=1/2 C_Dv²Aρ

However, we are talking about rotational motion, the torque related to the drag force given as

τ ∝ rv²Aρ

Since the motion is rotational motion, thus the angular velocity of the object can be related to the linear velocity as

v=ω×r, where r is the radius of the rotational path and ω is the angular velocity associated with the rotating object.

fairground gbbdbc9801 640 — **Image Credits: Image by dday1971 from Pixabay**

Substituting the value of v, we get

τ ∝ r³ ω²Aρ

From the above expression, the drag force is equivalent to the torque acting on the rotating object.

Thus the drag force can be written as

F_D=1/2 C_Dr³ ω²Aρ

Drag force and terminal velocity

When an object falls freely from the fluid, the maximum velocity acquired by the object is called terminal velocity.

Consider an example of a skydiver; when he dives, he falls under the influence of gravity. There are two forces are acting on the diver, one is force of gravity, and another one is drag force. However, as the velocity of the diver increases, the magnitude of the drag force is also increased until it becomes equal to the magnitude of gravitational force.

sky diving ga4188940f 640 — **Image credits: Image by Dimitris Vetsikas from Pixabay**

As the magnitude of drag and gravitational force becomes equal, the net force acting on the diver is nullified, making the acceleration also zero. At this instance, the diver has attained the constant velocity called terminal velocity.

Relationship between drag force and terminal velocity

In the previous section, we have discussed the relation between the drag coefficient and velocity and drag force and angular velocity. Similarly the relation between the drag force and the terminal velocity can be given by considering the falling object.

As we know, when the object attains the terminal velocity, it experiences two forces, drag and gravitational force. The gravitational force can be given by as weight of the object. So the net force is given by

F_net=W-F_D, where W=mg

As the object attains terminal speed, the net force F_net=ma=0

Thus F_D=W=mg

Substituting the above equation we get

F_D=1/2 C_{D V}T² Aρ

mg=1/2 C_{D V}T² Aρ

Rearranging the terms, we get terminal velocity as

v_T²=2mg/C_DAρ

v_T=√2mg/C_DAρ

What is drag force?

There is always a force of hindrance acting on the moving object, which offers resistance to the motion.

Drag force is exerted on the moving object in the fluid (liquid or gas). It can be defined as the force acting on the solid object moving in a fluid exerted opposite to the relative motion of the fluid.

Solved Problems On Drag force, Drag coefficient and Velocity

The drag force acting on a body is 235N, the density is given as 1.11kg/m³, and the cross-sectional area of the body is 2.33m². The body’s drag coefficient is calculated as 0.14 hence calculating the body’s velocity.

Solution:

The drag force F_D=235N

Density ρ=1.11kg/m³.

Cross-sectional are A=2.33m²

Drag coefficient C_D=0.14

The velocity of the body

v=√2F_D/C_D Aρ

v= √2(235)/(0.14) * 1.11 Aρ

v=36.02m/s.

Calculate the drag force of an object rotating in a circular path of radius 3m in the air with a speed of 12m/s. The area of cross-section is 3.4m², and the drag coefficient is 0.55.

Solution:

Drag coefficient C_D=0.55

Radius of the path r=3m

Cross-sectional area A=3.4m²

Angular velocity ω=12m/s

Density of air ρ=1.21kg/m³

F_D=1/2 C_Dr³ ω²Aρ

F_D=1/2 * 0.55 * 3³ * 12²* 3.4* 1.21

F_D=4.3×10³N

A diver of mass 79kg is diving from the parachute. The drag coefficient of the diver is given as 0.73, and the area of the cross-section is considered as 0.17m². Calculate the terminal velocity of the diver.

Solution:

Given –mass of the diver m=79kg

Drag coefficient C_D=0.73

Area of cross-section A=0.17m²

From the above data, the terminal velocity can be given as

v_T=√2mg/C_D Aρ

The density of air ρ=1.21kg/m³

Acceleration due to gravity g=9.8m/s²

v_T=√2(79*9.8)/0.73*0.17*1.21

v_T=101.600m/s.

Also Read:

How to Calculate Velocity in Topological Defects: A Comprehensive Guide

June 25, 2024February 18, 2022 by Core SME lambdageeks.com

Calculating the velocity of topological defects is a crucial aspect in understanding the dynamics of various systems, from liquid crystals to active matter. This comprehensive guide will provide you with the necessary tools and formulas to accurately determine the velocity of topological defects in your research. Dynamical Theory of Topological Defects The dynamics of topological … Read more

How To Find Acceleration With Velocity And Distance:3 Probs!

January 28, 2024February 16, 2022 by Alpa P. Rajai

To compute acceleration $a$ using initial velocity $u$ , final velocity $v$ , and distance $d$ , apply the formula $a = \frac{v^2 - u^2}{2d}$ . This equation originates from the kinematic relation $v^2 = u^2 + 2ad$ , assuming linear motion and constant acceleration. Acceleration, being a vector, encompasses both magnitude and direction; this formula calculates the magnitude. In cases of non-uniform acceleration, integration of the velocity function $v(t)$ is necessary. Consistent unit usage is crucial: $v$ and $u$ in meters per second ( $\text{m/s}$ ), $d$ in meters ( $\text{m}$ ), yielding $a$ in meters per second squared ( $\text{m/s}^2$ ).

How to find acceleration with velocity and distance without time

To find acceleration without time, use $a = \frac{v^2 - u^2}{2s}$ , where $a$ is acceleration, $v$ final velocity, $u$ initial velocity, $s$ distance. This derives from $v^2 = u^2 + 2as$ , a kinematic equation for constant acceleration, ensuring precise calculation when time data is unavailable.

How to find acceleration with distance time and initial velocity

To find acceleration with distance, time, and initial velocity, use $a = \frac{2(s - ut)}{t^2}$ . Here, $a$ is acceleration, $s$ distance, $u$ initial velocity, $t$ time. This formula accurately calculates acceleration, particularly in linear motion with uniform acceleration, providing a precise assessment in scenarios where final velocity is unknown.

Acceleration: A Quantitative Overview

Formula Derivation

Acceleration, denoted as a, is defined as the rate of change of velocity (v) over time (t). In situations where only velocity and distance (s) are known, the equation used is:

$a=2sv2−u2$

Here, v is the final velocity, u is the initial velocity, and s is the distance covered.

Underlying Physics

This formula is derived from kinematic equations under constant acceleration, integrating the principle of work-energy where the kinetic energy difference equates to the work done against the force causing acceleration.

Advanced Calculation Techniques

Case Study: Variable Acceleration

In cases of variable acceleration, calculus is employed. The velocity function v(t) is integrated over time to find distance, and its derivative gives acceleration:

$\int f(x) \, dx$

$s = \int v(t) \, dt$

$a(t) = \frac{dv(t)}{dt}$

Real-World Example: A Car’s Acceleration

For instance, a car accelerating from 0 to 60 km/h over 100 meters. Using our formula:

$a = \frac{(60^2 - 0^2) \times \left(\frac{5}{18}\right)^2}{2 \times 100} \approx 2.47 \, \text{m/s}^2$
$a = \frac{2 \times 100}{(60^2 - 0^2) \times \left(\frac{18}{5}\right)^2} \approx 2.47 \, \text{m/s}^2$

Practical Application: Experimental Approach

Setup and Measurement Techniques

Equipment: Motion sensor, track, and data analysis software.
Procedure: Release an object on the track, recording its velocity.
Data Analysis: Plot velocity vs. time, calculate acceleration.

Experiment: Verifying Theoretical Values

Conduct experiments, e.g., an object sliding down an inclined plane, measure the distance and final velocity, then calculate and compare the theoretical and experimental acceleration.

Challenges in Accurate Determination

Factors Affecting Accuracy

Air Resistance: Affects results, especially at high velocities.
Measurement Errors: Inaccurate distance or velocity measurements lead to erroneous acceleration calculations.
Friction: Introduces opposing force, affecting acceleration.

The Constant Acceleration Equations OR The Kinematics Formulas:

Kinematics formulas that are only relevant when an object or body moves with a constant acceleration within a given time interval are known as constant acceleration equations. When it comes to constant acceleration, the acceleration caused by gravity is the best real world example. It is commonly symbolized by the letter ‘g,’ whose value on the earth’s surface is 9.8 m/s².

The kinematic formulas, often known as constant acceleration equations, are a series of formulas that link the five kinematic variables given below.

a Constant Acceleration
v₀ Initial Velocity
v Finale Velocity
t Time Interval
ð›¥x Distance traveled by an object in one direction

Suppose an object or body is under constant acceleration, and three of these five kinematic variables (a, v, v₀, t, x) are known. In that case, we can use the kinematic equations given below to solve one of the unknown variables.

1. v = v₀ + at

2. ð›¥x = v₀t + (1/2)at²

3. v² = v₀² + 2að›¥x

How do you choose and apply a constant acceleration formula?

In kinematics, we have three equations of constant acceleration. Out of five kinematic variables, four are present in each equation.

We must select the constant acceleration equation that incorporates both the unknown variable we are looking for and three of the known kinematic variables. By introducing known variable values into the equation, we can find the unknown variable that is only unknown in the equation.

Consider the case of dragging a box that was initially steady. After 5 seconds, its velocity had increased to 10 m/s. Consider a constant acceleration for 5 seconds. Because we have v₀, v, and t, we can find the value of the unknown constant acceleration by applying the equation v = v₀ + at.

Let us see some problems of finding acceleration using velocity and distance.

But our primary concern for this article is to figure out how to calculate acceleration using velocity and distance. So, let us now talk about how to find acceleration with velocity and distance.

How to find acceleration with velocity and distance?

The constant acceleration equation is the one that is used in kinematics to find acceleration using velocity and distance.

If we have an initial velocity, a final velocity, and a distance but don’t know the time interval, we can apply the constant acceleration equation v² = v₀² + 2að›¥x to get the acceleration.

We have three known quantities and one unknown quantity in the above equation. We can calculate the constant acceleration by placing all three known values in an equation and making acceleration the subject of the equation. As a result, acceleration is determined by rearranging the above equation and given by:

We can find acceleration with velocity and distance using the equation above. Keep in mind that the constant acceleration equations only work if the acceleration is constant (as the name suggests) and in one direction. When dealing with two-dimensional or three-dimensional motion, things become more complicated. However, by applying the above equations for constant acceleration, one may build equations of motion for each direction separately. These simple equations aren’t used when acceleration is changing; instead, complex calculus is used.

Problem: A bike constantly accelerates from rest to a speed of 10 m/s across a distance of 20 m. Determine the acceleration of the bike.

Given:

The initial velocity of the bike v₀ = 0 m/s (As initially, the bike is at rest)

Finale velocity of the bike v = 10 m/s

Distance traveled by the bike ð›¥x = 20 m

To Find:

Constant acceleration of the bike a = ?

Solution:

Putting the values in the above equation:

âˆ´ a = 2.5 m/s²

As a result, the bike’s acceleration is 2.5 m/s².

Problem: From a height of 1.40 meters, a feather is dropped onto the moon. If the feather’s velocity is 2.135 m/s, then determine the acceleration of gravity on the moon.

Image Credits: Wikipedia

Given:

Initial velocity of the feather v₀ = 0 m/s (As in free falling initial velocity is zero)

Finale velocity of the feather v = 2.135 m/s

Distance traveled by the feather ð›¥x = 1.40 m

To Find:

Acceleration due to gravity on the surface of the moon a = ?

Solution:

Putting the values in the above equation:

âˆ´ a = 1.625 m/s²

Problem: At a speed of 12 m/s, a racing boat crosses the finish line and continues straight ahead. It came to a halt 18 meters from the finish line. What is the magnitude of the acceleration of the racing boat if it instantly decelerates till it comes to a stop?

Given:

Initial velocity of the racing boat v₀ = 12 m/s

Explore the advanced science and research posts to learn more.

Finale velocity of the racing boat v = 0 m/s (As it comes to a stop)

Distance traveled by the racing boat ð›¥x = 18 m

To find:

Constant acceleration of the racing boat a = ?

Solution:

Putting the values in the above equation:

âˆ´ a = -4 m/s²

The negative sign indicates that the racing boat’s acceleration decreases and its value is 4 m/s².

We hope we have answered all of your questions on how to find acceleration with velocity and distance.

Explore the advanced science and research posts to learn more.

Also Read:

A Comprehensive Guide on How to Find Velocity in Biophysics

June 25, 2024February 16, 2022 by Core SME lambdageeks.com

Summary Biophysics is a multidisciplinary field that combines the principles of biology and physics to study the physical aspects of living organisms. One of the fundamental quantities in biophysics is velocity, which is crucial for understanding various biological processes, from blood flow to cellular dynamics. In this comprehensive guide, we will explore several measurable and … Read more

How to Calculate Constant Velocity

The Equation for Constant Velocity

How to Use the Constant Velocity Formula

Worked Out Examples on Calculating Constant Velocity

Factors Influencing Constant Velocity

Role of Acceleration in Constant Velocity

Impact of Friction on Constant Velocity

How Distance and Time Affect Constant Velocity

Practical Applications of Constant Velocity

Checking Constant Velocity Joint

Finding Constant Velocity in Physics

Using Constant Velocity in Real-World Scenarios

Numerical Problems on how to find constant velocity

Problem 1:

Problem 2:

Problem 3:

Uniform Circular Motion

Examples of Uniform Circular Motion

Formulas and Calculations

Angular Velocity in Rotating Systems

Examples of Constant Angular Velocity in Rotating Systems

Theoretical Explanation

Formulas and Calculations

Numerical Problems and Data Points

Conclusion

References

Relation between drag coefficient and velocity

Drag force and velocity relationship

How does velocity affect drag?

Drag force and angular velocity

Drag force and terminal velocity

Relationship between drag force and terminal velocity

What is drag force?

Solved Problems On Drag force, Drag coefficient and Velocity

The drag force acting on a body is 235N, the density is given as 1.11kg/m3, and the cross-sectional area of the body is 2.33m2. The body’s drag coefficient is calculated as 0.14 hence calculating the body’s velocity.

Calculate the drag force of an object rotating in a circular path of radius 3m in the air with a speed of 12m/s. The area of cross-section is 3.4m2, and the drag coefficient is 0.55.

A diver of mass 79kg is diving from the parachute. The drag coefficient of the diver is given as 0.73, and the area of the cross-section is considered as 0.17m2. Calculate the terminal velocity of the diver.

How to find acceleration with velocity and distance without time

How to find acceleration with distance time and initial velocity

Acceleration: A Quantitative Overview

Formula Derivation

Underlying Physics

Advanced Calculation Techniques

Case Study: Variable Acceleration

Real-World Example: A Car’s Acceleration

Practical Application: Experimental Approach

Setup and Measurement Techniques

Experiment: Verifying Theoretical Values

Challenges in Accurate Determination

Factors Affecting Accuracy

The Constant Acceleration Equations OR The Kinematics Formulas:

How do you choose and apply a constant acceleration formula?

How to find acceleration with velocity and distance?

Problem: A bike constantly accelerates from rest to a speed of 10 m/s across a distance of 20 m. Determine the acceleration of the bike.

Problem: From a height of 1.40 meters, a feather is dropped onto the moon. If the feather’s velocity is 2.135 m/s, then determine the acceleration of gravity on the moon.

Problem: At a speed of 12 m/s, a racing boat crosses the finish line and continues straight ahead. It came to a halt 18 meters from the finish line. What is the magnitude of the acceleration of the racing boat if it instantly decelerates till it comes to a stop?

The drag force acting on a body is 235N, the density is given as 1.11kg/m³, and the cross-sectional area of the body is 2.33m². The body’s drag coefficient is calculated as 0.14 hence calculating the body’s velocity.

Calculate the drag force of an object rotating in a circular path of radius 3m in the air with a speed of 12m/s. The area of cross-section is 3.4m², and the drag coefficient is 0.55.

A diver of mass 79kg is diving from the parachute. The drag coefficient of the diver is given as 0.73, and the area of the cross-section is considered as 0.17m². Calculate the terminal velocity of the diver.