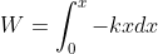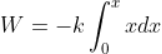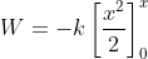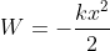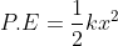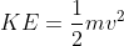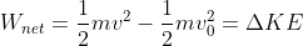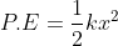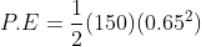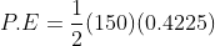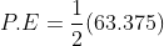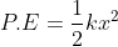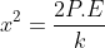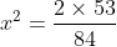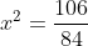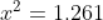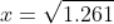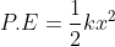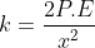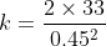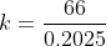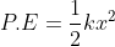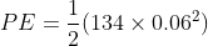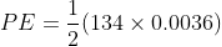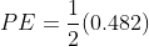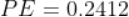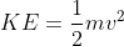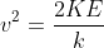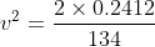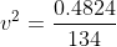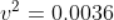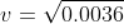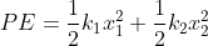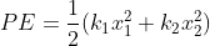Physics

Force being a vector quantity has both magnitude and direction. The measure or size of force acting on an object is known to be the magnitude of force.

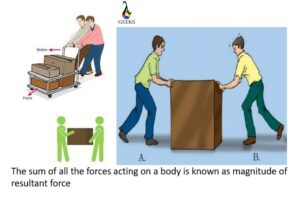
The vector sum of forces that act on a body is the magnitude of resultant force. At a given time, there are always multiple forces working on a body. Either they act in the same direction or the opposite directions. The combination of all the forces keeps the object stable and does the work.

In physics, the single force that generates the same effect as multiple forces are known as the magnitude of the resultant force. Force, being a vector quantity, is important to consider the direction of a force. The forces that act in the same direction are taken as positive, and those acting in opposite directions are negative. The restaurant force is also known as the net force.

To understand the concept of the magnitude of resultant force, let us take a simple example.

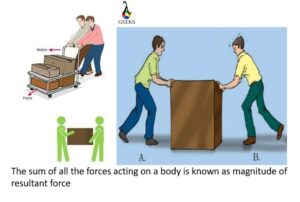
Two to three people are required to lift a heavy box. But if there is an extremely strong bodybuilder, he can easily lift the box. Hence the force exerted by the bodybuilder would be almost equal to the force exerted by all the other people. And it would be the magnitude of resultant force

Numerically the resultant force is written as;

F = f₁ + f₂+ f₃

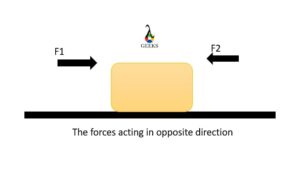
When the force on the body acts in the opposite direction, they are subtracted to generate the net force.

F = f₁ – f₂

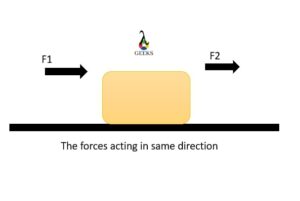
When the force acts in a particular direction, they add up to get the magnitude of the resultant force.

F = f₁ + f₂

Classification of Resultant Force

The magnitude of the resultant force classifies it into;

• Balanced Force
• Unbalanced Force

Balanced Force

When the net force acting on a body equals zero, it is known as balanced force. Here forces are equal in magnitude but act in the opposite direction. If the force is balanced, the body will continue to remain in the position of rest or motion. There would be no acceleration.

Some instances of balanced force are;

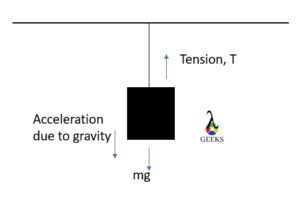
In the above diagram, we can see that the weight of the body pulls it downwards, but due to the tension on the rope, it does not fall. Hence the magnitude of the resultant force acting on the body is zero.

Even the log floating on water is possible due to the balanced force. The weight of the log acts downwards, but the upthrust pulls it upwards. Hence the net force is zero, and the log floats on water. If the weight exceeds the upthrust, then the log will sink into the water.

A box resting on a table experiences a normal force that acts upwards and gravity downwards. Both the forces balance each other, and hence the magnitude of resultant force is zero.

Unbalanced Force

The unbalanced force has a magnitude not equal to zero. When the force acting in opposite or the same direction sums up generation acceleration, it is known to be the magnitude of the resultant force. The unbalanced force either moves a stationary object or changes the velocity of the body. The acceleration or change in a direction totally depends on the measure of the resultant force. Greater magnitude generates great deflection.

To understand the concept of an unbalanced force, look at these everyday activities;

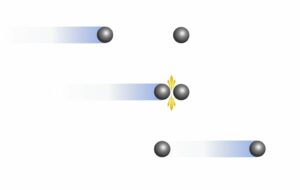
The tug of war is the most basic instance of the resultant force. Once the two teams exert the same measure of force, but in opposite directions, no one moves. But the second any team generates more force than the other, the resultant force gets unbalanced, and they are able to pull the other team.

The moving car also experiences multiple forces. The engine applies a force that moves the car forward, but at the same time, the friction opposes its motion. Since the magnitude of the forward force is much greater than the friction force, it gets unbalanced. Hence the car moves towards the direction of restaurant force.

The apple falling on the ground is due to the magnitude of the resultant force. The gravity pulls the apple downwards, and the normal force acts upwards. But the strength of gravity is much greater than the normal force that the net force acts downwards.

Therefore, to sum up, the balanced and unbalanced force;

• Forces of equal magnitude acting in the opposite direction have resultant magnitude zero and no acceleration.
• Forces of unequal magnitude acting in opposite directions are subtracted, and the body accelerates towards the greater force.
• Force of unequal magnitude acting in the same direction adds up, and the body accelerates towards the resultant force.

Frequently Asked Question (FAQs)

What is the magnitude of force?

The external or internal strength acting on a body to bring necessary changes is known to be the force.

The measure of force is known as its magnitude. It is the numerical value that provides us with the idea of how much energy or strength is applied to do the work. For example, the force applied on the brake to stop the car is its magnitude.

What is the magnitude of resultant force?

The size or measure of force is known as the magnitude of force.

When two or more force acts on a body the total sum of the force that generates an effect on it, is known as the magnitude of resultant force. In simpler words, the sum of the total force is the resultant force. For example, when two people try to push the box in the same direction, their forces add up to generate resultant force. It helps them to push the box easily.

Are net force and resultant force equal?

The sum of all the forces acting on a body is known as resultant force.

The net force is the addition of the total force. Numerically it is the same as the resultant force. The net force is just the other name for the resultant force.

What happens when the magnitude of the resultant force is zero?

All the force acting on a body is added up to get the magnitude of resultant force.

When the magnitude of resultant force is zero, the body does not move, or there is no acceleration. The body remains in the same position of rest or motion. For example, the book kept on a table experiences normal force and gravitational pull. Both the forces are equal in magnitude and opposite in direction, and hence the resultant force adds up to zero.

How do balanced and unbalanced forces differ?

The resultant force is of two types; balanced and unbalanced force.

The balanced force has a net magnitude of zero, and the body does not accelerate. The unbalanced force has non-zero magnitude, and the body changes the velocity. When the cyclist rides a bicycle, he generates an unbalanced force that makes the cycle move. When he stops pedaling, the bicycle stops as the friction force and applied force gets balanced.

Is air resistance a balanced force?

The opposing force generated by the air on the moving body is air resistance.

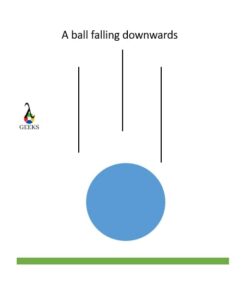
To answer this question, let us take an example. When a ball falls downwards, it experiences air resistance and gravitational pull. The pull is of greater extent, and therefore the ball accelerates downwards. But there comes a time when the ball stops accelerating and just keeps falling down with the same velocity. It is at this time that the force becomes balanced.

How do unbalanced forces accelerate the body?

When the sum of force acting in the same or opposite direction is not zero, it is known as an unbalanced force.

When the net force is not zero, then there is some force acting on a body that will cause changes. Through a simple physics concept, we know that the body moves in the direction of greater magnitude. Hence the body changes velocity and accelerates towards the resultant force. It proves Newton’s First Law of Motion.

The magnitude of force refers to the strength or intensity of a force. It is a crucial concept in physics that helps us understand how objects interact with each other. The magnitude of force can be measured in various units, such as Newtons (N) or pounds (lbs). In this article, we will explore different examples of magnitude of force and how it affects the motion and behavior of objects. Understanding the magnitude of force is essential in fields like engineering, mechanics, and even everyday life situations. So, let’s dive in and explore some fascinating examples of the magnitude of force in action.

Key Takeaways

• The magnitude of force is a measure of the strength or intensity of a force.
• Examples of forces with large magnitudes include the force exerted by a rocket engine, the force of a car crashing into a wall, and the force exerted by a weightlifter lifting heavy weights.
• Forces with small magnitudes include the force exerted by a person pushing a door open, the force of gravity pulling an object downward, and the force of a pencil resting on a table.
• The magnitude of force can be calculated using Newton’s second law, which states that force is equal to mass multiplied by acceleration.

How to Find Magnitude of Force Examples

In the world around us, forces are constantly at play. From the gentle push of a breeze to the powerful pull of gravity, forces shape our everyday experiences. Understanding the magnitude of these forces is crucial in many fields, such as physics, engineering, and even sports. In this section, we will explore how to find magnitude of force examples by identifying everyday situations involving force, analyzing the forces involved in each situation, and determining the magnitude of force exerted in each situation.

Identifying Everyday Situations Involving Force

To begin our exploration of force examples, let’s take a moment to consider the various situations in which forces are at play. Forces can be found in countless scenarios, both big and small. Here are a few examples to help illustrate the point:

1. Throwing a Ball: When you throw a ball, you exert a force on it. The force you apply determines how far and how fast the ball will travel.

2. Lifting a Weight: When you lift a weight at the gym, you are exerting a force against the force of gravity. The heavier the weight, the greater the force required to lift it.

3. Driving a Car: When you press the accelerator pedal in a car, you apply a force that propels the vehicle forward. The force you exert determines how quickly the car accelerates.

4. Opening a Door: When you push or pull a door to open it, you apply a force to overcome the resistance of the door’s hinges and any friction present.

5. Jumping: When you jump, you exert a force against the ground, propelling yourself upward. The force you apply determines how high you can jump.

These examples highlight just a few everyday situations where forces are at play. By recognizing these scenarios, we can delve deeper into analyzing the forces involved.

Analyzing the Forces Involved in Each Situation

Now that we have identified some everyday situations involving force, let’s take a closer look at the forces at play in each scenario. By analyzing these forces, we can gain a better understanding of their magnitude. Let’s examine the forces involved in the examples mentioned earlier:

1. Throwing a Ball: When you throw a ball, several forces come into play. The force of your arm propels the ball forward, while gravity pulls it downward. Air resistance also acts upon the ball, opposing its motion through the air.

2. Lifting a Weight: When you lift a weight, the force you exert opposes the force of gravity pulling the weight downward. The magnitude of the force required depends on the weight of the object.

3. Driving a Car: When you press the accelerator pedal, the engine exerts a force that propels the car forward. Friction between the tires and the road also affects the force required to move the car.

4. Opening a Door: When you push or pull a door, the force you exert overcomes the resistance of the door’s hinges and any friction present. The force required depends on the weight and size of the door.

5. Jumping: When you jump, the force you apply to the ground propels you upward. Gravity acts as a downward force, opposing your upward motion. The force required to jump higher depends on factors such as leg strength and technique.

By analyzing the forces involved in each situation, we can now move on to determining the magnitude of force exerted.

Determining the Magnitude of Force Exerted in Each Situation

To determine the magnitude of force exerted in each situation, we need to consider the relevant factors and apply the appropriate formulas or calculations. Here are some ways to determine the magnitude of force in the examples we discussed:

1. Throwing a Ball: The magnitude of the force exerted when throwing a ball can be calculated using Newton’s second law of motion, which states that force equals mass multiplied by acceleration. By measuring the mass of the ball and the acceleration it experiences, we can determine the force exerted.

2. Lifting a Weight: The magnitude of the force required to lift a weight can be determined by measuring the weight of the object. The force exerted is equal to the weight of the object multiplied by the acceleration due to gravity.

3. Driving a Car: The magnitude of the force exerted when driving a car can be calculated by considering factors such as the mass of the car, the acceleration applied, and any resistive forces like friction. Newton’s second law of motion can be applied to determine the force exerted.

4. Opening a Door: The magnitude of the force required to open a door can be determined by considering factors such as the weight of the door, the distance from the hinges, and any friction present. By applying the principles of torque and equilibrium, we can calculate the force required.

5. Jumping: The magnitude of the force exerted when jumping can be determined by considering factors such as the mass of the person, the acceleration applied, and the height of the jump. Again, Newton’s second law of motion can be applied to calculate the force exerted.

By applying the appropriate formulas and calculations, we can determine the magnitude of force exerted in each situation. This knowledge is valuable in various fields and can help us better understand the world around us.

Magnitude of Force Examples

Pushing a Table

Pushing a table may seem like a simple task, but it involves various forces at play. When you push a table, you exert a force on it to overcome the force of static friction. Static friction is the force that prevents the table from moving when it is at rest.

Muscles in your body generate the necessary force to push the table. When you contract your muscles, they pull on your tendons, which in turn pull on your bones. This action creates a force that is transmitted to your hands, allowing you to exert force on the table. The magnitude of force you apply depends on factors such as the weight of the table and the coefficient of friction between the table and the floor.

Friction plays a crucial role in determining the magnitude of force required to push the table. If the coefficient of friction is high, it will be more challenging to move the table, and you will need to apply a greater force. On the other hand, if the coefficient of friction is low, it will be easier to push the table, and a smaller force will be sufficient.

Lifting a Box

Lifting a box off the ground involves overcoming the force of gravity. When you lift a box, you exert an upward force that counteracts the downward force of gravity. This force is generated by the muscles in your body.

Your muscles contract, pulling on your tendons and bones, which allows you to generate the necessary force to lift the box. The magnitude of force required depends on the weight of the box. Heavier boxes require a greater force to lift, while lighter boxes require less force.

Drawing Water from a Well

Drawing water from a well often involves the use of ropes and pulleys to exert force. When you pull on the rope, the force is transmitted through the rope to the pulley system. The pulleys multiply the force, making it easier to lift the water.

The magnitude of force required to draw water from a well depends on various factors, such as the weight of the water and the efficiency of the pulley system. A well-designed pulley system can significantly reduce the force needed to lift the water.

Swimming in a Pool

Swimming in a pool involves experiencing several forces. One of these forces is buoyant force, which acts in the upward direction and counteracts the weight of your body. Buoyant force allows you to float in the water.

To move forward while swimming, you need to overcome fluid friction. When you move your arms and legs, you generate a force that propels you through the water. The magnitude of force required to swim depends on factors such as your body size, swimming technique, and the resistance offered by the water.

Playing Cricket

Cricket involves various forces that come into play during the game. When a bowler throws the ball, it experiences the force of air resistance. Air resistance acts in the opposite direction to the ball’s motion, slowing it down.

To hit the ball, a batsman needs to generate a force with the cricket bat. The magnitude of force required depends on factors such as the speed and trajectory of the ball, as well as the desired distance and direction of the hit.

Riding a Bicycle

Riding a bicycle involves the application of force to move forward. When you pedal, you convert the energy from your muscles into kinetic energy, propelling the bicycle forward. The force you apply to the pedals is transmitted through the chain to the wheels, causing them to rotate.

Friction plays a crucial role in maintaining speed and starting the bike. The force of friction between the tires and the road allows the bike to grip the surface and move forward. Without friction, it would be challenging to ride a bicycle.

Squeezing a Lemon

Squeezing a lemon involves applying force to extract the juice. When you squeeze the lemon, you apply a muscular force to compress it. This force causes the lemon to deform, releasing the juice contained within.

The magnitude of force required to squeeze a lemon depends on factors such as the ripeness of the fruit and the desired amount of juice. Ripe lemons are easier to squeeze, requiring less force, while unripe lemons may require more force to extract the juice.

Applying Brake to a Vehicle

Applying the brake to a vehicle involves the generation of friction force to stop its motion. When you press the brake pedal, it activates the brake system, which applies friction to the wheels. This friction force opposes the vehicle‘s motion, eventually bringing it to a stop.

The magnitude of force required to stop a vehicle depends on factors such as its speed, mass, and the efficiency of the braking system. Higher speeds and heavier vehicles require a greater force to stop within a given distance.

Towing a Car

When it comes to towing a car, there are various forces at play that allow for the successful movement of one vehicle by another. Let’s take a closer look at the different aspects involved in this process.

Description of the Force Involved in Towing

Towing a car requires the application of a force known as tension force. This force is exerted on the tow bar, which is connected to both the towing vehicle and the car being towed. The tension force acts in the direction of the tow, allowing the towing vehicle to pull the other car along.

Role of Tension Force in Accelerating the Vehicles

The tension force plays a crucial role in accelerating both the towing vehicle and the car being towed. As the towing vehicle exerts a force on the tow bar, the tension force transfers this force to the car being towed. This transfer of force causes the car to accelerate and move in the same direction as the towing vehicle.

Balancing Tension Force on the Tow Bar

To ensure a smooth and safe towing experience, it is important to maintain a balanced tension force on the tow bar. If the tension force is too high, it can lead to excessive strain on the tow bar and potentially cause damage. On the other hand, if the tension force is too low, the car being towed may not move effectively. Finding the right balance is crucial for a successful towing operation.

Frequently Asked Questions

Q1: What is the magnitude of force?

The magnitude of force refers to the size or strength of a force. It is a scalar quantity that represents the amount of push or pull exerted on an object.

Q2: How can I find the magnitude of a force?

To find the magnitude of a force, you can use the formula: magnitude = mass × acceleration. This formula applies to forces acting in a straight line.

Q3: Can you provide some examples of force magnitude?

Certainly! Here are a few examples of force magnitude:

• Pushing a car with a force of 500 Newtons.
• Pulling a suitcase with a force of 50 Newtons.
• Lifting a weight with a force of 1000 Newtons.

Q4: Are there any illustrations or demonstrations of force magnitude?

Yes, there are various ways to illustrate or demonstrate force magnitude. For example, you can use a spring scale to measure the force required to stretch or compress a spring. Another demonstration involves using a force sensor to measure the force exerted by an object.

Q5: Can you provide some instances or cases of force magnitude?

Certainly! Here are a few instances or cases of force magnitude:

• Calculating the force required to accelerate a rocket into space.
• Determining the force needed to lift a heavy object.
• Measuring the force exerted by a person while pushing a shopping cart.

Q6: How can I find the magnitude and direction of a resultant force?

To find the magnitude and direction of a resultant force, you can use vector addition. This involves adding the individual forces together using the rules of vector addition. The magnitude of the resultant force can be found using the Pythagorean theorem, and the direction can be determined using trigonometry.

Q7: Are there any examples of magnitude and direction of resultant force?

Certainly! Here are a few examples of magnitude and direction of resultant force:

• Two forces of 10 Newtons and 15 Newtons acting at an angle of 30 degrees to each other.
• Three forces of 20 Newtons, 30 Newtons, and 40 Newtons acting at different angles to each other.

Q8: Can you provide some force magnitude exemplifications?

Certainly! Here are a few force magnitude exemplifications:

• Calculating the force required to stop a moving car.
• Determining the force needed to launch a rocket into orbit.
• Measuring the force exerted by a person while lifting weights.

Q9: Are there any force magnitude representations?

Yes, there are various ways to represent force magnitude. One common representation is using vector diagrams, where the length of the arrow represents the magnitude of the force. Another representation is using numerical values with appropriate units, such as Newtons (N) or pounds (lb).

Q10: Can you provide some force magnitude samples?

Certainly! Here are a few force magnitude samples:

• Calculating the force required to move a heavy object across a frictional surface.
• Determining the force needed to stretch a spring to a certain length.
• Measuring the force exerted by a person while rowing a boat.

Force can be classified as internal or external forces. We will be discussing the types of the latter, one that is an external force.

The external force is exerted between the body and the surrounding. It occurs when the force is applied to any object from outside and is non-conservative. The change in velocity is the basic effect caused by external forces. The types of external forces are:

• Friction Force
• Normal Force
• Air Resistance Force
• Applied Force
• Tension

Friction force

When an object moves over a surface, then a restricting force emerges that tries to oppose the motion of the body. This force is known as the Force of Friction or Frictional Force. Some of the kinetic energy of the body is converted into heat energy to obstruct the motion and get lost. Hence frictional force is non-conservative.

The basic example of friction is the lightning of a matchstick. When we rub the stick on the surface, friction comes into play and converts kinetic energy into heat that ignites the matchstick. Friction also helps us to walk and write.

The friction force is dependent on the factors; normal force and a coefficient of friction µ.

The straightforward formula for friction is:

Where,

N is the normal force acting perpendicularly to the surface

µ is the coefficient of friction, and its value completely depends on the surface.

The frictional force can be classified into given four categories:

• Static Friction
• Sliding Friction
• Rolling Friction
• Fluid Friction

Normal Force

The normal force acts on every object perpendicularly to keep them from falling off and at a stable position. It only comes into the act when the body and surface are in contact with each other. For example, a book lying on a table experiences gravitational force downwards but does not fall. The normal force pulls upwards to keep it off from falling. It is generated by the surface of the object. Every object, even humans too, experiences the normal force, and it is a non-conservative force.

From the diagram we can see:

Where,

N is the normal force

m is the mass of the body

g is the acceleration due to gravity.

From the free-body diagram:

On splitting W into two components, we get:

Here,

N = normal force

m = mass

g = acceleration due to gravity

Θ = angle between the inclined surface

Air Resistance Force

The external force caused by the body flying or moving through the air is known as air resistance force or air drag. It acts in the opposing direction of the motion of the object.  The resistance is also caused due to the collision of air molecules and the object’s surface. Hence, this force depends on two factors; the velocity of the moving body and the area of the object. That is why all the aircraft and birds have a streamlined front to reduce the area, which leads to less air resistance force and hence their easy movement. 

The force of air resistance is given as:

Here,

F_air = air resistance force

c = force constant

v = velocity of the object

The negative sign indicates that the direction of the force air resistance is opposite to the motion of the object.

Applied Force

The simple external push and pull force that is applied to the object is applied force. It tends to move the body at rest or change the velocity of the moving body. The applied force can be classified into contact and non-contact forces. The contact force is the type of external force. The applied force can be differentiated as:

• Pull: When the force is applied to move the object towards oneself. Example: Pulling the rope

• Push: When the force is applied in such a way to move the object in the forward direction and away from oneself. Example: Pushing the box.

• Collision: when two bodies collide with each other, they both exert force on each other. The collision tends to change the velocity and direction of the collided bodies. The collision can be elastic and inelastic.

According to the second law of motion, the formula of applied force is:

Where,

F = applied force

m = mass of the body

a = acceleration produced.

Tension

When a load is attached to any kind of string, cable, rope, or similar object, a pulling force is exerted along the length of the object in the upward direction. In physics, this force is known as tension. It is important to remember that tension does not apply on its own; it has to be provided to the system. While explaining the concept of tension force, we take the string to be massless so that the applied tension is equally transmitted to the whole string. Some of the examples of tension force are:

• Tug of war
• Towing of car
• Pulling a box with the help of a rope.

From the free diagram, the formula for tension can be determined as:

Where,

T= tension force

m=mass of the body

g= acceleration due to gravity

Types of Friction Force

Static Friction

Static friction comes into play when the body and the surface area are at the rest position with respect to each other. This force helps the object to avoid any trigger caused by applied forces. The object only comes into motion when the applied force exceeds the static force.

The basic example of static friction is pushing a heavy box. The static friction does not allow the motion of the box. It is only when two or three people come together and apply greater force than the static friction that the box moves. 

Other examples are:

• Book on a table
• Clothes hanging on the rack
• A car parked on a hill

The value of static friction is calculated from the formula:

To move the object, the inequation is given as:

Here,

F_s is the static friction

µ_s is the coefficient of static friction

N is the normal force acting perpendicularly to the surface

Sliding friction

When an object slides over another body or surface, then the opposition that is created against the motion is known as the sliding friction.

An example of sliding friction is ice skating. When a person pushes the ice skate forward by applying their weight, sliding friction is created. It generates the heat energy that melts the ice and helps in sliding the skate easily.

More example of sliding friction is:

• Sliding book over the table
• Rubbing of rag on the counter
• Sliding through a slide
• Sliding car on the ramp

The formula for sliding friction is given as:

Here,

F_s = sliding friction

µ_s = coefficient of sliding friction

N = normal force

Rolling friction

The friction that acts on a body when it rolls over a surface is known as rolling friction or rolling drag. When an object rolls over a surface, both of them get deformed at the point of contact that tends to create motion below the surface.

It is due to the rolling friction that a rolling ball stops after some time. Without friction, the ball would keep rolling forever. Other examples of rolling friction are:

• The wheels of all the vehicles generate rolling friction
• Rolling of pencil

The formula for rolling friction is:

Where,

F_r is the rolling friction

µ_r is the coefficient of rolling friction

N is the normal force

Fluid friction

Friction not only opposes the movement of solid objects. The layers of liquid when slide against each other, friction is generated between them known as fluid friction. It also restricts the movement of other objects into the liquid.

The fluid friction restrains the movement of swimmers, and hence it requires much energy for swimming in water. Also, the water gushing around their body is due to fluid friction. The other examples of this friction are:

• Stirring of a spoon into coffee or milk
• Movement of the submarine through the water.

Frequently Asked Question (FAQs)

What is external force?

A body can experience a force in two ways externally and internally. 

The force exerted from outside on any object is known to be an external force. It can be a contact force as well as a non-contact force. Mostly external force is contact force and comes into action when an object interacts with its surroundings. Pushing a table and car are some examples of external force. 

Is external force conservative or non-conservative?

The conservation of energy classifies the force as conservative and non-conservative. 

When an object experiences the external force, energy is generated, and work is done on it. In doing the work, some of the energy gets dissipated. Hence the total energy before and after the force is applied does not remain the same. Therefore, an external force is non-conservative. 

What are the types of external force?

The external force is of the following five types:

• Friction
• Tension
• Normal force
• Air resistance 
• An applied force. 

What are the effects of external force?

The external force generally tends to change the velocity of the moving body. 

What are the advantages of friction?

The opposing force acting on a moving object is called friction.  

Friction is a necessary phenomenon that makes our everyday work easier. When we walk on the ground, the friction caused by the ground on our feet helps in walking by pushing us forward. It also helps us to write, in skiing and many other things. 

How can friction be of disadvantage?

Friction makes our everyday work possible, but it also causes some damage.

The opposition generated on the moving body by friction is done by converting kinetic energy into heat energy. The heat causes unnecessary wear and tear of objects and also reduces the working efficiency of the machines. In order to subdue the friction, a lot of energy is required. 

Do you know what force will known as Conservative force?

Firstly you must have to understand what is conservative force. When an object is moving from one point to another the net work by a force exerting on the object is depends only on its starting point and the ending point not on the path traced then the force is called as the Conservative Force.

In the above figure the object traces three different path, but the work done on the object is same at three path also, it is because the work done is independent of the path through which it is travelling.

Now we shall move to the concept of  spring force. When an elastic body is stretched or compressed by an object having certain mass the force exerted on the elastic body to displace some distance is called Spring force. Here in this article we are going to know is spring force is a conservative or not.  

Is spring force conservative

Conservation of potential energy:

 A conservative force gives rise to the concept of potential energy (P.E) of the system. If the potential energy of any force is zero then it must be a non conservative. To know is spring force is conservative or not we must check whether the potential energy of the spring is zero or not.

Let us consider a spring which stretches or compresses or elongate at certain distance. A stretched object is considered as elastic medium which obeys Hooke’s Law. The force acting on the spring to stretch from its original position is given by

                          F_spring =  kx

Where x is the displacement when the spring is elongated or compressed, k is the spring constant.

Since the compressed spring stretches by applying some force in opposite direction then the force will be

                      F =  – kx

Here we consider the spring as massless object whose force will be same or constant at every point on the spring.

The total work done to stretch the spring from its initial position to its final position is given by

The net work done on the stretched or compressed spring is equal to the potential energy of the spring is it is given by\\

(Here we neglect the negative sign because energy can not be negative)

The potential energy of the spring force is non zero quantity. It shows that potential energy of the spring force is conserved.

Conservation of kinetic energy:

The energy caused by the motion of the system is called the kinetic energy. From the theory of  work-energy the is equal to its change kinetic energy.

As we know the kinetic energy is due to the motion of the system given by

Where v is the speed at which the spring is displaced. And m is the mass of the spring.

The net work done on the spring system when is displaced from original position to final position is given by the change in kinetic energy  as

Where ∆KE is the change in the kinetic energy, v₀ and the v is the speed of displacement of the spring from original point to final point.

If only conservative force is acts on the spring system then the work done will  be

W_net = W_con  ; where  W_con  is the total work done by all the forces of the system.

i.e;  W_con  = ∆KE

The kinetic energy of the spring system is non zero.

It shows that the kinetic energy of the spring is a conserved quantity.

When the spring begins to displace from original position it loses the potential energy. Then the network done will be  

W_con = -∆PE

Or -∆PE = ∆KE

Or ∆PE+∆KE = 0

The above equation implies that the total energy of the system ( i.e; potential energy and the kinetic energy ) is constant for the spring force system. The total energy of the any system is conserved force.

Hence it shows that the spring force is also a conservative force.

Some solved examples:

A spring is stretched at a distance of 0.65m whose spring constant is 150Nm^-1. calculate the potential energy of the spring system.

Solution:

           Given : Displacement of the spring = 0.65m

                         Spring constant k = 150Nm^-1

The potential energy of the spring is given by

P.E = 31.687J

The spring constant of a stretched spring is 84Nm^-1 and the potential energy is calculated as 53J. find the displacement of the spring.

Solution :

            Given :  The spring constant k = 84Nm^-1

                           Potential energy (P.E) = 53J

The potential energy of spring is given by

To find the displacement we have to rearrange the above equation as

Substituting the values

Taking the square root

The displacement x = 1.12m

A spring is attached to a slab. It uses the energy of 33J to stretch 45cm. Calculate the spring constant using potential energy formula of the spring force .

Solution:

            Given : Potential energy of the spring = 33J

                          Displacement of the spring = 45m = 0.45m

To calculate the spring constant, the potential energy of the spring is

Rearranging the equation

k = 325.92Nm^-1

A toy is pulled by a spring whose force constant is 134N/m . It is displaced a distance of 6cm. Calculate the kinetic energy and the speed of the toy that displaced through?

Solution:

           Given : Force constant k = 134N/m

                         Displacement of the toy = 6cm = 0.06m

 The total energy of the spring system is given by

 KE = – PE

The potential energy energy of the system is

i.e; KE= PE

KE = 0.2412

Here we neglect the negative sign because the kinetic energy can not be negative.

Kinetic energy is given byKinetic energy is given by

The speed or the velocity is given by

Taking the square root on both side

v = 0.6 m/s²

The toy moves with a speed of 0.6 m/s² .

Two spring of spring constant k₁ and k₂ are attached to a rigid support vertically. It has the displacement of x₁ and x₂ respectively. What will be the net force acting on the springs? And what is the potential energy of the system?

Here we just have to resolve the spring force equation.

Let the two spring attached to a rigid support be s₁ and s₂.

The force acting on s₁ will be

F₁ =  k₁x₁     …..(1)

The force acting on  s₂ will be

F₂ = k₂x₂    ……(2)

From equation (1) and (2) the net force acting on the spring is given by

F = F₁ + F₂

F =  k₁x₁ + k₂x₂

The total potential energy of the system can be given as

By knowing values we can solve the potential energy.

Calculate the force required for a spring to stretch when the it is expanded at a distance of 26cm and having the spring constant 93N/m

Given : Displacement of the spring = 26cm = 0.26m

              Spring constant k = 93N/m

By the formula of spring force

F = kx

F = 93 × 0.26

F = 24.18 N

Frequently Asked Questions on spring Force:

what do you mean by Spring Constant?

The spring constant is a measurement of stretching ability of the spring.

It can also be defined as The force that required for a spring to compress or to elongate or to stretch by certain distance is meant as spring constant.

What is Hooke’s Law?

Hooke’s law is stated as the amount of force required to expand or compress  an elastic body is directly proportional to the distance at which the body is expanded or stretched.

Dose the gravity affect the spring constant?

Gravity does not affect the spring constant however  Gravity definitely affect the net force of spring as the gravity acts as a restoring force when the spring is suspended vertically from its equilibrium position.

What are the factors that influences the spring constant? 

Factors that influences the spring constants are

• diameter of the each coil of the spring.
• diameter of the suspension wire.
• length of the spring when at rest.

Acceleration is an example of a vector quantity i.e. “it comprises of both direction and magnitude”. The direction of an object’s acceleration is oriented towards the resultant force’s direction on the object. Mechanics defines acceleration as “The rate of variation of velocity with respect to time.”

According to Newton’s second law of motion, acceleration is given by the ratio of the net force acting over an object to the mass of the object. In other words, acceleration is also termed as the rate of change of velocity with respect to time i.e. dv/dt. The unit of acceleration is meter per second squared based on the standard international (SI) system.

We know that both force and velocity are vector quantities and both mass and time are scalar quantities. “When we divide a vector quantity by a scalar quantity it results in a vector quantity.” Hence mathematically, we can say that by the virtue of this property acceleration is also a vector quantity i.e. it has both direction and magnitude.

Physically, the force acting on an object can make it move or speed up towards the direction in which the resultant force lies. This means that the object starts to accelerate towards that direction upon the action of the resultant force. Since acceleration is equal to force by mass we can say that for an equal amount of force applied to different objects the acceleration of each object would depend on its mass.

Example of direction of acceleration

The direction of acceleration can be demonstrated with several examples such as:

• Let us consider a stationary ball kept on a table. If we apply horizontal force that is strong enough to counter the frictional resistance acting on the ball from the table surface, then and the ball will start to move in the direction of the horizontal force. Therefore, we can say that after the application of the horizontal force the ball starts to accelerate in the direction of the resultant force.

• Any free falling object in vacuum experiences an acceleration due to gravity that is always directed towards the center of the earth. A free falling object in air experiences to different kinds of acceleration: acceleration due to gravity and acceleration caused by the resistance buoyant force off the air or air resistance.

• Every form of circular motion including the ones in which this speed does not change has an acceleration. This is because in case of a circular motion direction of motion is continuously changing and this change is caused by an acceleration.

It should be noted that at rest, an object experiences two forces: gravity and normal, which cancels each other out maintaining its acceleration as zero.

What are the types of acceleration based on direction?

Based on the direction, acceleration can be categorized into three types

• Positive acceleration: the acceleration that acts on an object in the direction of the object’s initial propagation direction is called a positive acceleration. This type of acceleration increases the speed of the object towards its direction of propagation. At times this kind of acceleration is also termed linear acceleration. For example, this type of acceleration is observed when an accelerator is pressed in a moving vehicle to increase its speed.
• Negative acceleration: the acceleration that acts on an object in the direction opposite to the direction of the object’s initial propagation direction is called negative acceleration. This type of acceleration tends to slow down the speed of the object or bring it to a stop completely. At times, negative acceleration is also referred to as “deceleration or retardation”. For example, this type of acceleration is observed when brakes are applied in a moving vehicle to reduce its speed or make the vehicle stop.
• Radial acceleration: the acceleration that changes the direction of propagation of an object is called radial or orthogonal acceleration. This type of acceleration does not affect the speed of the moving object. For example, this type of acceleration is observed when a vehicle makes a turn at a constant speed.

Does average acceleration have direction?

Average acceleration is defined as the ratio of the change in velocity of an object to the duration of time.

Yes, average acceleration does comprise of a direction along with magnitude. “The direction of average acceleration is determined by the direction of the change in velocity over a period of time.” In case, the initial velocity is equal to zero or the object starts from a standstill, then the direction of average acceleration is equal to the direction of the final velocity of the object after a certain period of time.

Does acceleration have the same direction as velocity?

No. It would not be correct to say that the direction of acceleration is always equal to the direction of velocity.

In the practical world, by acceleration, we generally mean the average acceleration of an object. Therefore, the direction of acceleration is towards “the direction of change in velocity”. However, in the case of instantaneous acceleration i.e. the acceleration of a body at a given point of time, we can say that the direction of velocity and acceleration is the same.

Another point to be noted is that acceleration is said to have the same direction as that of velocity when acceleration causes the magnitude of the velocity i.e. speed of an object to increase. However, acceleration is said to have the opposite direction as that of velocity when acceleration causes the magnitude of the velocity i.e. speed of an object to decrease.

How is the direction of the average acceleration determined?

The average acceleration of an object is given by the change in velocity by the duration of time i.e.

Here, ∆v is the change in velocity and ∆t is the duration of time. The direction of acceleration is given by the direction of the ∆v vector. If ∆v1 vector and ∆v2 vector are given, then we can find out ∆v vector by the triangle law of vectors. The graphical representation of the direction of acceleration in terms of the direction of the change in velocity is shown in the figure below:

What is tangential acceleration?

The term tangential acceleration is valid for a circular path.

Tangential acceleration is defined as “the rate of change of the tangential velocity of an object traveling in a circular path having a radius R, with respect to time”. Tangential acceleration is somewhat analogous to linear acceleration. Tangential acceleration is responsible for varying only the magnitude of the velocity i.e. speed of an object.

Mathematically, the tangential acceleration of an object is given by the equation:

Tangential acceleration = radius of the rotation (R) x angular acceleration (α)

What is centripetal acceleration?

The term centripetal acceleration is valid for a uniform circular motion.

Centripetal acceleration is defined as “the ratio of the square of the velocity of an object traveling in a circular path to the radius of the circular path”. Centripetal acceleration is responsible for changing the direction of the velocity of an object traveling in a circular path. The magnitude of acceleration does not change due to centripetal acceleration.

Mathematically, centripetal acceleration is given by

Centripetal acceleration = V²/R

We hope this post could answer all your queries related to the direction of acceleration.

Tension force is a fundamental concept in physics and engineering that describes the pulling or stretching force in an object or system. It arises when an object is subjected to an external force that attempts to elongate or compress it. Understanding how to calculate tension force is crucial for various applications, from analyzing the stability of structures to determining the forces within complex mechanical systems.

In this blog post, we will delve into the different scenarios where tension force calculations are applicable. We will explore the formulas, equations, and step-by-step methods to calculate tension force in various situations. Through examples and explanations, we will demystify this concept and equip you with the tools to confidently calculate tension forces.

The Formula for Calculating Tension Force

The Basic Tension Force Formula

The tension force, denoted by T, can be calculated using the following formula:

Where:
– T represents the tension force.
– F is the applied force that is responsible for creating the tension.
– θ denotes the angle between the direction of the applied force and the direction of the object or system.

The sine function accounts for the component of the applied force that contributes to the tension force.

How to Use the Tension Force Formula

To use the tension force formula, follow these steps:

1. Identify the applied force F and the angle θ between the force and the object or system.
2. Substitute the values into the tension force formula: .
3. Calculate the value of T using the appropriate units.

Examples of Tension Force Calculations

Let’s consider a few examples to illustrate the calculation of tension force using the formula.

Example 1:
Suppose a person pulls a crate with a force of 50 Newtons at an angle of 30 degrees with the horizontal. To find the tension force in the rope, we can use the tension force formula:

Simplifying this equation, we find:

In this case, the tension force in the rope is 25 Newtons.

Example 2:
Consider a scenario where a cable is supporting a hanging mass with a force of 100 Newtons at an angle of 60 degrees with the vertical. By applying the tension force formula, we can determine the tension force in the cable:

Solving this equation:

Thus, the tension force in the cable is approximately 86.6 Newtons.

Calculating Tension Force in Different Scenarios

Now that we understand the basic tension force formula, let’s explore how it can be applied in various scenarios. We will discuss specific situations where tension force calculations are crucial and provide step-by-step methods for calculation.

How to Calculate Tension Force in a String

Tension force calculations in a string are relatively straightforward. The tension force in the string is equal at all points along the string, assuming it is massless and inextensible. Therefore, to calculate the tension force in a string, you can use the same tension force formula we discussed earlier.

How to Calculate Tension Force in a Cable

When dealing with cables, such as those used in suspension bridges or cranes, we can calculate the tension force by considering the forces acting on the cable. The tension force in the cable would be equal to the sum of all the forces acting on it, such as the weight of the hanging object or the external forces applied.

How to Calculate Tension Force in a Spring

In the case of a spring, the tension force is determined by Hooke’s Law, which states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position. The tension force in a spring can be calculated using the formula:

Where:
– T represents the tension force.
– k is the spring constant, which characterizes the stiffness of the spring.
– x denotes the displacement from the equilibrium position.

How to Calculate Tension Force in an Atwood Machine

An Atwood machine involves two masses connected by a string or a rope passing over a pulley. The tension force in such a system can be calculated by considering the difference in masses and the acceleration of the system. The formula to calculate tension force in an Atwood machine is dependent on the specific configuration and can be derived using Newton’s second law and the principles of equilibrium.

How to Calculate Tension Force on an Inclined Plane

When an object is placed on an inclined plane and connected to a string, the tension force in the string can be calculated by considering the forces acting on the object. By analyzing the forces along the inclined plane, including the component of the weight parallel to the plane, the tension force can be determined.

How to Calculate Tension Force of a Hanging Mass

When a mass is hanging vertically from a string or a cable, the tension force in the string can be calculated by considering the weight of the mass and the acceleration due to gravity. The tension force will be equal to the weight of the mass.

How to Calculate Tension Force Between Two Objects

In situations where two objects are connected by a string or a cable, the tension force can be calculated by considering the forces acting on each object. By analyzing the forces involved, including the weight of the objects and any external forces applied, the tension force can be determined.

How to Calculate Tension Force in a Pulley System

Pulley systems are commonly used in mechanical systems to transmit forces and change the direction of motion. To calculate the tension force in a pulley system, you need to consider the masses involved, the number of pulleys, and any external forces applied. The equations for calculating tension forces in pulley systems can be derived using Newton’s second law and the principles of equilibrium.

How to Calculate Tension Force with Friction

When friction is present in a system, such as a block sliding on a surface with a tension force, the calculation of tension force becomes more complex. In such cases, you need to consider the forces due to friction and the normal force acting on the object. The tension force can be determined by analyzing the forces involved and applying the appropriate equations.

How to Calculate Tension Force at an Angle

When the tension force is applied at an angle to the direction of the object or system, the tension force formula we discussed earlier can be used. By considering the magnitude of the applied force and the angle between the force and the object, the tension force can be calculated.

How to Calculate Tension Force in Circular Motion

In situations involving circular motion, such as a mass rotating in a horizontal circle connected by a string or a cable, the tension force can be calculated by considering the centripetal force required to keep the object in circular motion. By equating the tension force with the centripetal force, the tension force can be determined.

Worked Out Examples

Let’s now work through some examples to solidify our understanding of tension force calculations in different scenarios.

Example of Calculating Tension Force in a String

Suppose we have a string connecting two objects with masses of 5 kg and 8 kg. The objects are hanging vertically, and we want to calculate the tension force in the string. We know that the acceleration due to gravity is 9.8 m/s².

To calculate the tension force, we need to consider the weight of each object. The tension force will be equal to the sum of the weights of the objects:

Substituting the given values:

Therefore, the tension force in the string is 127.4 Newtons.

Example of Calculating Tension Force on an Inclined Plane

Consider an object with a mass of 10 kg placed on an inclined plane with an angle of 30 degrees. The object is connected to a string, and we want to calculate the tension force in the string. Given that the acceleration due to gravity is 9.8 m/s², we can determine the tension force.

To calculate the tension force, we need to consider the forces acting on the object. These forces include the component of the weight parallel to the inclined plane and the normal force. By analyzing the forces, we can find the tension force:

Substituting the given values:

Therefore, the tension force in the string is 49 Newtons.

Example of Calculating Tension Force in a Pulley System

Let’s consider a pulley system with two masses connected by a rope passing over the pulley. The first mass has a weight of 5 kg, while the second mass has a weight of 8 kg. We want to calculate the tension force in the rope.

To calculate the tension force, we need to consider the forces acting on each mass. The tension force in the rope will be equal at both ends, so we can set up the following equations:

Since the tension force is equal at both ends, we can equate the two equations:

Simplifying the equation, we find:

This equation is not possible, indicating that there is no solution. In this case, the tension force in the pulley system cannot be determined without additional information.

Example of Calculating Tension Force with Friction

Suppose we have a block of mass 2 kg sliding on a horizontal surface. The block is connected to a string, and a tension force of 10 Newtons is applied at an angle of 30 degrees with the horizontal. The coefficient of friction between the block and the surface is 0.2. We want to calculate the tension force in the string.

To calculate the tension force, we need to consider the forces acting on the block. These forces include the tension force, the weight of the block, and the force of friction. By analyzing the forces, we can determine the tension force:

Where:
– T is the tension force.
– f_f represents the force of friction.
– m is the mass of the block.
– a is the acceleration of the block.

We can calculate the force of friction using the equation:

Where:
– μ is the coefficient of friction.
– N represents the normal force.

Since the block is on a horizontal surface, the normal force is equal to the weight of the block:

Substituting the values, we find:

Now we can calculate the force of friction:

Next, we can calculate the acceleration of the block:

Finally, we can solve for the tension force:

Therefore, the tension force in the string is 6.08 Newtons.

Example of Calculating Tension Force at an Angle

Consider a situation where an object of mass 5 kg is hanging from a string at an angle of 45 degrees with the vertical. We want to calculate the tension force in the string.

To calculate the tension force, we can use the tension force formula we discussed earlier:

Substituting the given values:

Therefore, the tension force in the string is approximately 34.3 Newtons.

In this blog post, we have explored the concept of tension force and how to calculate it in various scenarios. We began with the basic tension force formula, which considers the applied force and its angle of application. We then delved into specific scenarios, such as tension force in strings, cables, springs, pulley systems, and more. Through examples and step-by-step calculations, we have demonstrated how to determine tension forces accurately.

Understanding tension force and its calculations is essential for engineers, physicists, and anyone dealing with mechanical systems. By mastering these concepts and formulas, you will be better equipped to analyze and design structures, machines, and systems that rely on tension forces. So, the next time you encounter a situation involving tension forces, you’ll feel confident in calculating them accurately.

Numerical Problems on how to calculate tension force

Problem 1:

A rope of length 10 meters is tied to a support at one end and a block of mass 5 kg is attached to the other end. The block is being pulled horizontally with a force of 20 N. Calculate the tension force in the rope.

Solution:
Given:
Length of the rope,
Mass of the block,
Force being applied,

To calculate the tension force in the rope, we can use the equation:

Where:
is the tension force,
is the applied force,
is the mass of the block, and
is the acceleration due to gravity.

Substituting the given values:

Simplifying:

Therefore, the tension force in the rope is 69 N.

Problem 2:

A block of mass 2 kg is suspended by two ropes as shown in the figure. Find the tension forces in ropes A and B.

(https://i.imgur.com/HG9jXPZ.png)

Solution:
Let’s consider the tension force in rope A as and the tension force in rope B as .

For equilibrium, the sum of the forces in the vertical direction should be zero.

Similarly, the sum of the forces in the horizontal direction should also be zero.

We can solve these two equations simultaneously to find the values of and .

Simplifying the equation for the vertical direction:

Simplifying the equation for the horizontal direction:

We can solve these equations to find the values of and .

Problem 3:

A 10 kg mass is suspended from a vertical rope. Find the minimum tension force in the rope required to keep the mass stationary.

Solution:
When the mass is stationary, the tension force in the rope should balance the weight of the mass.

Let’s assume the tension force in the rope is . The weight of the mass is given by , where is the mass and is the acceleration due to gravity.

For the mass to be stationary, the tension force should be equal to the weight of the mass:

Substituting the given values:

Simplifying:

Therefore, the minimum tension force in the rope required to keep the mass stationary is 98 N.