Point Sections Or Ratio Formulae: 41 Critical Solutions

Basic Examples on the Formulae “Point sections or Ratio”

Case-I

Problems 21: Find the coordinates of the point P(x, y) which internally divides the line segment joining the two points (1,1) and (4,1) in the ratio 1:2.

Solution: We already know,

If a point P(x, y) divides the line segment AB internally in the ratio m:n,where coordinates of A and B are (x₁,y₁) and (x₂,y₂) respectively. Then Coordinates of P are

and

(See formulae chart)

Using this formula we can say , (x₁,y₁) ≌(1,1) i.e. x₁=1, y₁=1 ;

(x₂,y₂)≌(4,1) i.e. x₂=4, y₂=1

and

m:n ≌ 1:2 i.e m=1,n=2

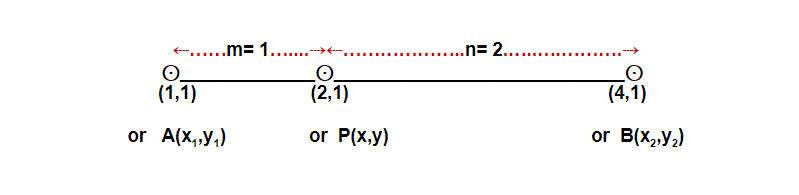
Therefore,

x =

( putting values of m & n in

Or, x =1*4+2*1/3 ( putting values of x₁ & x₂ too )

Or, x = 4+2/3

Or, x = 6*3

Or, x = 2

Similarly we get,

y =

( putting values of m & n in y =

Or, y =(1*1+2*1)/3 ( putting values of y₁ & y₂ too )

Or, y = 1*1+2/3

Or, y = 3/3

Or, y = 1

Therefore, x=2 and y=1 are the coordinates of the point P i.e. (2,1). (Ans)

More answered problems are given below for further practice using the procedure described in above problem 21:-

Problem 22: Find the coordinates of the point which internally divides the line segment joining the two points (0,5) and (0,0) in the ratio 2:3.

Ans. (0,2)

Problem 23: Find the point which internally divides the line segment joining the points (1,1) and (4,1) in the ratio 2:1.

Ans. (3,1)

Problem 24: Find the point which lies on the line segment joining the two points (3,5,) and (3,-5,) dividing it in the ratio 1:1

Ans. (3,0)

Problem 25: Find the coordinates of the point which internally divides the line segment joining the two points (-4,1) and (4,1) in the ratio 3:5

Ans. (-1,1)

Problem 26: Find the point which internally divides the line segment joining the two points (-10,2) and (10,2) in the ratio 1.5 : 2.5.

_____________________________

Case-II

Problems 27: Find the coordinates of the point Q(x,y) which externally divides the line segment joining the two points (2,1) and (6,1) in the ratio 3:1.

Solution: We already know,

If a point Q(x,y) divides the line segment AB externally in the ratio m:n,where coordinates of A and B are (x₁,y₁) and (x₂,y₂) respectively,then the coordinates of the point P are

and

(See formulae chart)

Using this formula we can say , (x₁,y₁) ≌(2,1) i.e. x₁=2, y₁=1 ;

(x₂,y₂)≌(6,1) i.e. x₂=6, y₂=1 and

m:n ≌ 3:1 i.e. m=3,n=1

Point sections — Graphical Representation

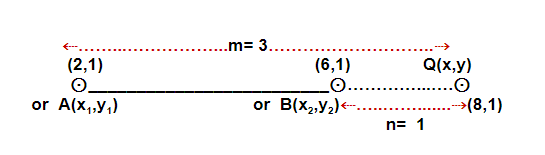
Therefore,

x =

( putting values of m & n in x =

Or, x =(3*6)-(1*2)/2 ( putting values of x₁ & x₂ too )

Or, x = 18-2/2

Or, x =16/2

Or, x = 8

Similarly we get,

y =

( putting values of m & n in y =

Or, y =

( putting values of y₁ & y₂ too )

Or, y = 3-1/2

Or, y = 2/2

Or, y = 1

Therefore, x=8 and y=1 are the coordinates of the point Q i.e. (8,1). (Ans)

More answered problems are given below for further practice using the procedure described in above problem 27:-

Problem 28: Find the point which externally divides the line segment joining the two points (2,2) and (4,2) in the ratio 3 : 1.

Ans. (5,2)

Problem 29: Find the point which externally divides the line segment joining the two points (0,2) and (0,5) in the ratio 5:2.

Ans. (0,7)

Problem 30: Find the point which lies on the extended part of the line segment joining the two points (-3,-2) and (3,-2) in the ratio 2 : 1.

Ans. (9,-2)

________________________________

Case-III

Problems 31: Find the coordinates of the midpoint of the line segment joining the two points (-1,2) and (1,2).

Solution: We already know,

If a point R(x,y) be the midpoint of the line segment joining A(x₁,y₁) and B(x₂,y₂) .Then coordinates of R are

and

(See formulae chart)

Case-III is the form of case-I while m=1 and n=1

Using this formula we can say , (x₁,y₁) ≌(-1,2) i.e. x₁=-1, y₁=2 and

(x₂,y₂)≌(1,2) i.e. x₂=1, y₂=2

Screenshot 11 — Graphical Representation

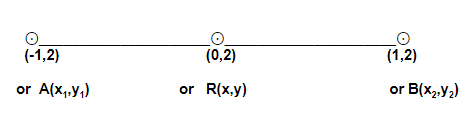
Therefore,

x =

( putting values of x₁ & x₂ in x =

Or, x = 0/2

Or, x = 0

Similarly we get,

y =2+2/2 ( putting values of y₁ & y₂ in y =

Or, y = 4/2

Or, y = 2

Therefore, x=0 and y=2 are the coordinates of the midpoint R i.e. (0,2). (Ans)

More answered problems are given below for further practice using the procedure described in above problem 31:-

Problem 32: Find the coordinates of the midpoint of the line joining the two points (-1,-3) and (1,-4).

Ans. (0,3.5)

Problem 33: Find the coordinates of the midpoint which divides the line segment joining the two points (-5,-7) and (5,7).

Ans. (0,0)

Problem 34: Find the coordinates of the midpoint which divides the line segment joining the two points (10,-5) and (-7,2).

Ans. (1.5, -1.5)

Problem 35: Find the coordinates of the midpoint which divides the line segment joining the two points (3,√2) and (1,3√2).

Ans. (2,2√2)

Problem 36: Find the coordinates of the midpoint which divides the line segment joining the two points (2+3i,5) and (2-3i,-5).

Ans. (2,0)

Note: How to check if a point divides a line (length=d units) internally or externally by the ratio m:n

If ( m×d)/(m+n) + ( n×d)/(m+n) = d , then internally dividing and

If ( m×d)/(m+n) – ( n×d)/(m+n) = d , then externally dividing

____________________________________________________________________________

Basic Examples on the Formulae “Area of a Triangle”

Case-I

Problems 37: What is the area of the triangle with two vertices A(1,2) and B(5,3) and height with respect to AB be 3 units in the coordinate plane ?

Solution: We already know,

If “h” be the height and “b” be the base of Triangle, then Area of the Triangle is = ½ × b × h

(See formulae chart)

image?w=366&h=269&rev=57&ac=1&parent=1Ug0lE5AOAhO4i0HE5fVqVUKTEbR0on8yfNNyWgAF Po — Graphical Representation

Using this formula we can say ,

h = 3 units and b = √

$(x2-x1)2+(y2-y1)2 $

i.e √

$(5-1)2+(3-2)2 $

Or, b = √

$(4)2+(1)2 $

Or, b = √

$(16+1 $

Or, b = √ 17 units

Therefore, the required area of the triangle is = ½ × b × h i.e

= ½ × (√ 17 ) × 3 units

= 3⁄2 × (√ 17 ) units (Ans.)

______________________________________________________________________________________

Case-II

Problems 38:What is the area of the triangle with vertices A(1,2), B(5,3) and C(3,5) in the coordinate plane ?

Solution: We already know,

If A(x₁,y₁) , B(x₂,y₂) and C(x₃,y₃) be the vertices of a Triangle,

Area of the Triangle is =|½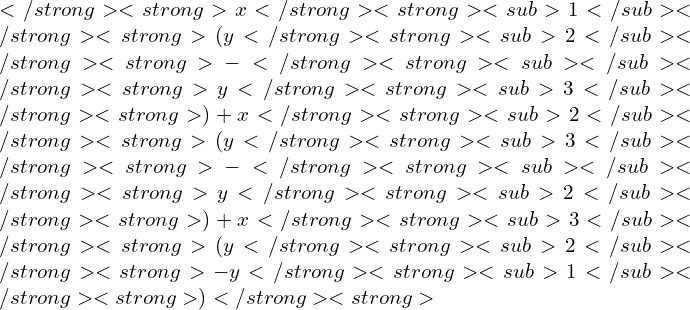

$x1 (y2- y3) + x2 (y3- y2) + x3 (y2- y1)$

(See formulae chart)

Using this formula we have ,

(x₁,y₁) ≌(1,2) i.e. x₁=1, y₁=2 ;

(x₂,y₂) ≌(5,3) i.e. x₂=5, y₂=3 and

(x₃,y₃) ≌(3,5) i.e. x₃=3, y₃=5

image?w=364&h=194&rev=207&ac=1&parent=1Ug0lE5AOAhO4i0HE5fVqVUKTEbR0on8yfNNyWgAF Po — Graphical Representation

Therefore, the area of the triangle is = |½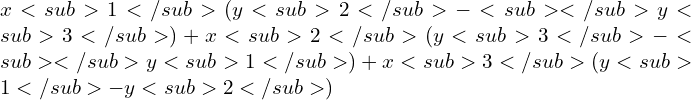

$x1 (y2- y3) + x2 (y3- y1) + x3 (y1-y2)$

| i.e

= |½

$1 (3-5) + 5 (5-3) + 3 (3-2)$

| sq.units

= |½

$1x (-2) + (5×2) + (3×1)$

| sq.units

= |½

$-2 + 10 + 3$

| sq.units

= |½ x 11| sq.units

= 11⁄2 sq.units

= 5.5 sq.units (Ans.)

More answered problems are given below for further practice using the procedure described in above problems :-

Problem 39: Find the area of the triangle whose vertices are (1,1), (-1,2) and (3,2).

Ans. 2 sq.units

Problem 40: Find the area of the triangle whose vertices are (3,0), (0,6) and (6,9).

Ans. 22.5 sq.units

Problem 41: Find the area of the triangle whose vertices are (-1,-2), (0,4) and (1,-3).

Ans. 6.5 sq.units

Problem 42: Find the area of the triangle whose vertices are (-5,0,), (0,5) and (0,-5). Ans. 25 sq.units

_______________________________________________________________________________________

For more post on Mathematics, please follow our Mathematics page.

NASRINA PARVIN

Hi….I am Nasrina Parvin. I have completed my Graduation in Mathematics, Having 10 years of experience working in the Ministry of communication and information technology of India. In my free time, I love to teach and solve math problems. From my childhood, Math is the only subject that fascinated me the most.