The triangle of power | Power voltage current triangle
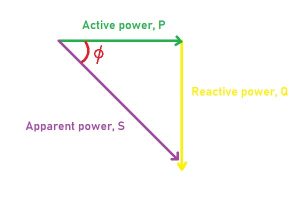
A power triangle is simply a rightangle triangle with side representing active power, reactive power, and apparent power. The base component symbolizes active power, the perpendicular component denotes reactive power, and the hypotenuse symbolizes apparent power.
What is power triangle?
Define power triangle | Power triangle definition
A power triangle is the graphical presentation of real or active power, reactive power, and apparent power in a right-angled triangle.
Power triangle equation | PQS power triangle
Power triangle formula calculation | Power triangle equation
In a power triangle, active power P, reactive power Q, and apparent power S form a right-angled triangle. Therefore,
hypotenuse2 = base2 + perpendicular2
S2 = P2 + Q2
Here, Apparent power(S) is measured in Volt-Ampere(VA).
Active power(P) is measured in Watt(W).
Reactive power(Q) is measured in Volt-Ampere reactive(VAR).
- A power triangle is the graphical presentation of real or active power, reactive power, and apparent power in a right-angled triangle.
- Active or true power refers to the entire amount of power dissipated in an electrical circuit. It is measured in Watt (W) or KiloWatt (KW) and represented with P and average value of the active power P.
- Reactive power or imaginary power is the power that doesn’t do any real work and causes zero power dissipation. T is also known as watt-less power. This is the power derived from reactive elements like the inductive load and the capacitive load. The reactive power is calculated in KiloVolt Amp reactive (KVAR) and is denoted by Q.
- The total power in the circuit, both absorbed and dissipated, is known as apparent power. The apparent power is computed by multiplying the r.m.s voltage with r.m.s current without any phase angle quantity.
- Ohm’s Law always works with DC circuits, but in the case of AC, it only works when the circuit is purely resistive, i.e., the circuit doesn’t have any inductive or capacitive load. But, most of the AC circuits consist of a series or parallel combination of RLC. Due to this, voltage and current become out of phase, and a complex quantity is introduced.
- The power of the three-phase system is = √3 x power factor x voltage x current.
Power triangle for RLC series circuit | Power triangle circuits
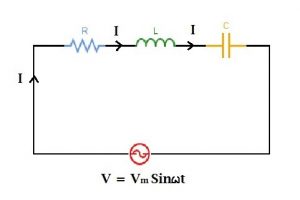
Let us consider an RLC circuit connected in series as above.
Where, a resistor with resistance R.
an inductor with inductance L.
a capacitor with capacitance C.
An AC voltage source Vmsin⍵t is applied.
V is the r.m.s value of applied voltage, and I is the r.m.s value of the total current in the circuit. The inductor and the capacitor produce XL and XC oppositions, respectively, in the circuit. Now, there can be three cases-
Case 1: XL > XC
Case 2: XL < XC
The power triangle is obtained from the phasor diagram, if we multiply each of the voltage phasors with I, we get three power components.
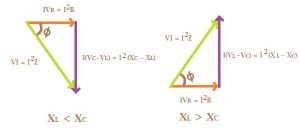
From the phasor triangle, we can quickly get the power triangle by multiplying the voltages with I. The real power is multiplied by VR, which is equal to I2R. The reactive power is I multiplied by (VC – VL), which is equal to I2(XC – XL). The apparent power V = I2Z is calculated from the active power and the reactive power for both cases, Here we take into consideration another quantity, the complex power. The complex power is the summation of the active power and the reactive power represented in complex form, i.e., with the ‘j’ quantity.
Therefore, complex power
S = P – jQ when XL < XC
S = P + jQ when XL > XC
Now, for case 1, inductive reactance is less than capacitive reactance. Therefore, reactive power is negative, and angle ϕ is also negative. For case 2, inductive reactance value is more than capacitive reactance value, reactive power is +ve, and angle ϕ is also +ve.
Active reactive apparent power triangle | Power volts amps triangle
Active power and reactive power triangle.
True power triangle.
Active or true power refers to the entire amount of power dissipated in an electrical circuit. It is measured in Watt (W) or KiloWatt (KW) and represented with P and average value of the active power P is,
P = VI = I2R
Reactive power triangle
Reactive power or imaginary power is the power that doesn’t do any real work and causes zero power dissipation. Itt is also known as watt-less power. This is the power derived from reactive elements like the inductive load and the capacitive load. The reactive power is calculated in Kilovolt Amp reactive (KVAR) and is denoted by Q.
Reactive power Q = VIreactive = I2X.
Apparent power triangle
The total power in the circuit, both absorbed and dissipated, is known as apparent power. The apparent power is computed by multiplying the r.m.s voltage with r.m.s current without any phase angle quantity.
Apparent power
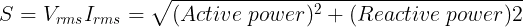
For a purely resistive circuit, there’s no reactive power. So, the apparent power is equal to active or true power.
Power triangle for AC circuit | Electrical power triangle
AC circuits can have any combination of R, L, and C and if we want to calculate the total power correctly, we have to know the phase-diff among the I and V. The waveform of the current and the voltage are sinusoidal. As the power = voltage x current, maximum power is obtained when both the waveforms coincide. In this situation, the waveform are called ‘in-phase’ with each other.
- In a purely resistive AC circuitry, the I and V perfectly align with each other in terms of phase. Therefore just by multiplying them, we can get the power.
- If the circuit has any inductive or capacitive load, a phase difference is created. Even if the phase difference is minute, AC power is divided into two parts- one positive and one negative. The negative power is not a mathematically negative quantity; it just implies that the power is provided to the system, but no energy transfer takes place. This power is known as reactive power. The positive quantity does some real work, so it is classified as real or active power.
- Another portion of power is provided to the circuit from the source. It is known as apparent power. The apparent power is calculated by multiplying the r.m.s values of the current and the voltage.
Ohm’s Law power triangle | Ohm’s power triangle
Ohm’s Law always works with DC circuits, but in the case of AC, it only works when the circuit is purely resistive, i.e., the circuit doesn’t have any inductive or capacitive load. But, most of the AC circuits consist of a series or parallel combination of RLC. Due to this, voltage and current become out of phase, and a complex quantity is introduced. We need to apply some special formulas in order to calculate the alternating current and parameters of the power triangle.
Power triangle for capacitive load
A capacitive load means that the power factor is leading as the current lead the voltage by the phase angle.
Power triangle for inductive load
An inductive load represent that the power factor is lagging because the I lags V by the phase angle.
Complex power triangle
Complex power is nothing but the representation of power using complex numbers. The real part represent the active power. Imaginary part represent the reactive power.
Let us assume that the current and the voltage in a capacitive circuit are I and V, respectively. We know, for capacitive load, the I leads the V by a phase angle. Let us take this angle as ϕ.
Let’s say the voltage across the load, V= vejƟ and current I = iej(Ɵ+ϕ).
We know, the power is the voltage multiplied by the current conjugate.
So complex power S = VI* = vejƟ x ie-j(Ɵ+ϕ)= vie-jϕ
S = vi(cosϕ – jsinϕ) = vicosϕ – jvisinϕ = P – jQ [we know active power P = vicosϕ and reactive power Q = visinϕ ]
For the capacitive load, the I lags V by the phaseangle. So, the voltage across the load, V= vejƟ and current I = iej(Ɵ-ϕ).
So complex power
S = VI* = vejƟ x ie-j(Ɵ-ϕ)= viejϕ
S = vi(cosϕ + jsinϕ) = vicosϕ + jvisinϕ = P + jQ
Three-phase power triangle
Alternating current can be single-phase or three-phase. The variation of current amplitude results in the generation of sine waves. For a single-phase supply, there’s just one wave. Three-phase systems split the current into three parts. The three current components are out-of-phase by one-third of a cycle each. Each current component is equal in size but opposite in direction to the another two conjunctive.
The power of the three-phase system is = √3 x power factor x voltage x current.
Impedance triangle and power triangle
Impedance triangle power factor
In DC circuits, only the resistance is responsible for opposing the current. But in AC circuits, a quantity called reactance also opposes the current. The reactance can be any combination of inductance and capacitance. But both the inductance and the capacitance differ from the resistance with a phase angle (lagging or leading). So, we cannot add them arithmetically. So, we construct an impedance triangle with hypotenuse Z(impedance), base R(resistance), and reactance X( inductive or capacitive reactance or both).
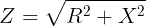
Power factor= R/Z
Power triangle power factor
The power factor in the power triangle is referred to as the ratio of active power and apparent power, defined as the cosine of the phasor angle.
Power factor correction triangle
The power factor correction is a method to increase the efficiency of an electrical circuit by reducing the reactive power. Power factor correction is achieved through parallel-connected capacitors that oppose the effects caused by inductive elements and decrease phase shift.
Power factor triangle formula
The power factor for capacitive or inductive load= R/Z
Power factor = Real power/Apparent power
Power energy triangle
Electrical energy is defined as the system’s power multiplied by the total time the power is used.
Energy E = P x T
How to draw a power triangle?
Power triangle generator
The power triangle is constructed by taking the active power as the base, the reactive power as perpendicular, and the apparent power as the hypotenuse.
Metal triangles on power lines
We often see a few triangular loops hanging from the power lines. These are used to provide stability to the lines in high wind. These triangular fins prevent the lines from bouncing too close to each other and ensure that they are not loosened from the insulators.
Electrical power triangle calculations | Power triangle calculator
Q. An inductor coil of 120 mH and a 70 ohm resistance are connected in series with a 220 volt, 50 Hz supply. Calculate the apparent power.
Inductive reactance
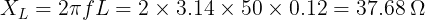
Impedance of the inductor
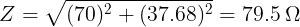
So, the current consumed by the inductor = V/Z= 220/79.5 = 2.77 A
Therefore, phase angle
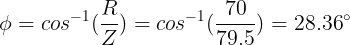
lagging
Active power
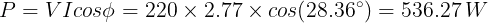
Reactive power
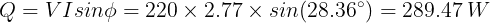
Apparent power
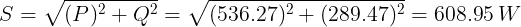
Q. Calculate the power factor of the series RLC circuit with inductive load 23 ohm, capacitive load 18 ohms, and resistive load 12 ohms connected with a 100 volt 60 Hz supply voltage.
Given:
Inductive reactance XL = 23 ohm
Capacitive reactance XC = 18 ohm
Resistance = 12 ohm
Total impedance of the circuit
Power factor of the circuit = R/Z = 12/13 = 0.92
Power triangle example
Q. A load of 20 kW is at a power factor 0.8 lagging. Find the capacitor rating so that it can raise the value of the power factor to 0.95.
Here, the true power P = 20 KW
Power factor cosϕ1 = 0.8
We know, the reactive power must be reduced to get an increased power factor. Therefore, the phase angle will also decrease. Let us assume that initially, the phase angle was ϕ1, and after reducing the reactive power, the phase angle is ϕ2. So, the power triangle looks like-
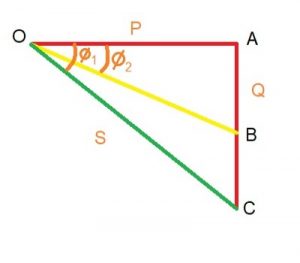
We can see from the diagram that the reactive power has decreased to AB from AC. So we need to compute the difference of AC and AB, and this quantity is the required capacitor rating.
Here, OA = 20 KW
cosϕ1 = 0.8
cosϕ2 = 0.95
We know, cosϕ1 = OA/OC
So, OC = 20/0.8 = 25 KVA
AC = √(OC2 – OA2) = 15 KVAR
Cosϕ2 = OA/OB
So, OB = 20/0.95 = 21 KVA
AB = √(OB2 – OA2) = 6.4 KVAR
Therefore, BC = AC – AB = (15 – 6.4) = 8.6 KVAR
FAQs
How many types of powers are there in the power triangle?
The power triangle consists of three types of power
- – True or active power.
- – reactive power.
- – apparent power.
What is power triangle? Explain active,reactive and apparent power with an exemplar.
The power triangle is the triangular representation of the relationship between the true power, the reactive power, and the apparent power.
For example, in any electrical appliance, the total power generated is the parts of the active and the reactive power.
What is the power triangle of an AC circuit?
The power triangle of an AC circuit can be resistive, capacitive, or Inductive and triangle consists of three kinds of powers, and the apparent power is computed with the help of the active power and the reactive power.
What is the power triangle of an RL circuit?
The RL circuit has a power triangle with the active power = I2R, the reactive power = I2XL, and the apparent power = I2Z, where XL is the Inductive reactance and Z is the total impedance of the circuit.
What is the relation between KVA, KW, & KVAr?
KVA is the unit of the apparent power, whereas KW and KVAR are the units of true power and reactive power, respectively. Therefore from the concept of the power triangle, we can conclude that KVA2 = KW2 + KVAR2.
What is the significance of the power factor?
For inductive and capacitive loads, the power factor plays a vital role in computing the reactive power. Reactive power is the part of active power that gets diminished and powerfactor is the ratio of the true power and the apparent power. The unity power factor indicate that the circuit is completely resistive in nature.
How many watts is 6 KVA?
6 KVA = 6000 VA
At unity power factor 6 KVA = 1 x 6000 = 6000 Watts
If the power factor is anything else, 6 KVA = 6 x (power factor) watts
How to convert KWH to KVAH?
KWH = KVAH X power factor
Therefore, KVAH = KWH/ power factor
How many watts does 1 kVA equal to?
For a purely resistive load, there’s no reactive power. So the power factor is 1. Here 1 kVA= 1 Watt
If the load is capacitive or inductive, the resistive power is not 0, as power factor is resistance/impedance. Here 1 kVA = power factor x 1 KW
Why are electric towers in triangular shapes?
For the following reasons, electric towers are triangular.
- Triangles have a greater base area which allows them to be highly rigid. This rigidity helps in withstanding side loadings.
- Triangles have less area than any quadrilateral. If the shape were quadrilateral, then the cost would have been more. The triangular shape reduces the cost by eliminating one extra side.
What is the power factor for a transformer?
The power factor of a transformer depends upon the characteristics of the load.
If the load is purely resistive, the power factor is Unity or 1.
If the load is capacitive, i.e., XC > XL, the power factor is known as leading.
If the load is inductive, i.e., XL > XC, the power factor is known as lagging.
What is the difference between KVA KWH KVAH and KVAR? | Power triangle KW KVA KVAR
KVA stands for Kilo Volt Ampere. This is the unit of real or active power.
KWH stands for Kilo Watt Hour. This is used to measure how much power(in kilowatts) is consumed in an hour.
KVAH stands for Kilo Volt Ampere Hour. KVAH is the apparent power, whereas KWH is the active power. KVAH = KWH/ power factor
KVAR stands for Kilo Volt Ampere reactive. It is used to measure reactive power.
What is the power factor of an L-R circuit?
The impedance of an L-R circuit is Z = R + jωL
We know, power factor
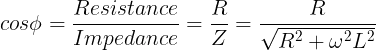
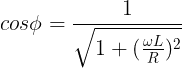
What is the unit of the power factor?
The power factor is the ratio of the active power (KW) and the apparent power (KVA) as both the numerator and the denominator are powers, the power factor is a unit less quantity.

Hi……I am Kaushikee Banerjee completed my master’s in Electronics and Communications. I am an electronics enthusiast and am currently devoted to the field of Electronics and Communications. My interest lies in exploring cutting-edge technologies. I’m an enthusiastic learner and I tinker around with open-source electronics.