Is Energy a Vector Quantity:Why,How,Detailed Facts

In Physics, the physical quantities are classified into two main categories: scalar and vector.

The quantity, which refers to magnitude and direction, is known as a vector, i.e. speed. And the quantity which only deals with the magnitude is known as a scalar quantity, i.e. mass, charge etc.

Energy is the physical quantity that gives the idea about the capacity of an object or system to do work.

In order to answer the question: is energy a vector quantity? , go through this post.

Is energy a vector quantity

In physics, energy is also defined as the work done on the system or body.

energy=work done

Work = force . displacement

If we apply force on a system or body and it gets displaced in the direction of force; then it is said to work has been done on the body.

Now, as we know, force and displacement both are vector quantities as it also requires direction to get the full detail of it. The dot product of two physical quantities such as force and displacement gives the scalar (ordinary) value—scalar quantity.

Hence, we can conclude, the physical quantity—Energy is NOT a Vector Quantity.

Why energy is a scalar quantity.

As we have studied that the energy, a physical quantity falls in the category of scalar quantity.

As we know the scalar quantities are associated only with the magnitude not with the direction and here, energy doesn’t have any direction.

In addition or subtraction of energies, the vector algebra is not applicable.

The formula of energy, evinces the dot product between the two physical quantities (force, displacement, which are vector).

Hence, the above points exhibit why energy is a scalar quantity.

Why energy is not a vector quantity.

Though energy has a particular direction in some cases. For example, Thermal energy where heat energy flows always from hotter body to cooler one.

But,

The addition or subtraction of the quantity is done by using ordinary law of algebra not vector algebra.

Energy always has positive, negative or zero real value only.

Let’s see few examples related to it.

Problem 1: A force F= i+2j+3k acts on a particle and the particle gets displaced to a distance S= 4i+6j. Find the work done on the particle if the force and displacement both are in the same direction.

Solution: Given quantities:

Force, F= i+2j+3k

Distance,s= 4i+6j

Now, work done on the body is given by

Work= force . displacement

W = (i+2j+3k). (4i+6j)

W = 4+ 12+0

W = 16J

Problem 2: A particle moves from position a= 3i+2j-6k to position b= 14i+13j-9k under the action of a force (4i+j+3k) newton. Calculate the work done.

Solution: Given quantities

Force, F= 4i+j+3k newton

a= 3i+2j-6k

b= 14i+13j-9k

r= b–a

r= (14i+13j-9k)-(3i+2j-6k) = 11i+11j-3k

W = F.r

W = (4i+j+3k).(11i+11j-3k)

W = 44+11-9 = 46 J

Problem 3: Find the work done in moving a particle along a vector s= 4i-j+7k meter, if the applied force is F= i+2j-k newton.

Solution: Given quantities,

Force, F= i+2j-k newton

s= 4i-j+7k meter

Now the work done is given by, W= Force*displacement

W= (i+2j-k)*(4i-j+7k)

W= 4-2-7 = -5 J

The work done in moving a particle is equivalent to the energy gained by the particle.

Problem 4: A body is constrained to move in the y-direction. It is subjected to a force (-2i+15j+6k) newton. What is the work done by the force in moving the body through a distance of 10m?

Solution: Given quantities:

Force F= -2i+15j+6k newton

Displacement s= 10j meter

Work done is given by, work= force*displacement

work= (-2i+15j+6k).10j

work= 150 J

Hence the work done on the body is 150 J.

Frequently asked questions: FAQs

Question. What is a dot product?

There are two ways to perform multiplication of two vector quantities and one of them is dot product.

The dot product, sometimes also known as—Scalar Product as we get a scalar quantity by multiplying two vectors. In vector algebra, we can’t multiply two vectors as we do in mathematics.

Dot product can be defined in two ways. One of them is algebraically–the summation of product of corresponding entries and the other is geometrically–the product of the magnitude of two vector quantities and the cosine angle between them.

The interesting feature of the dot product is that the resultant vector lies in the same plane.

The dot product of two vectors can have positive, negative or zero value.

Suppose a and b are two vectors, then its dot product can be written as

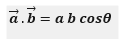
Dot product is also helpful to find out the projection (shadow) of one vector on another. When we say projection of one vector onto another it means that the shadow of the former vector on the latter one.The resultant vector has a scalar value.

Let AB = b and AC=a , are the two vectors and theta is the angle between them. Draw a normal BD on the AC line.

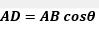
AD is the vector projection

a.b=a (projection of b on a)

Question. What is a cross product?

The other way of performing multiplication of two vector quantities is cross product also called as — Vector product.

As the resultant quantity obtained is a vector one. It is found in a plane which is normal to both the vectors and to know its direction, one need to use a profound or basic rule—right hand thumb rule.

Hence, the cross product happens to be in three dimensions while the dot product is confined to two dimensions only.

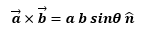
Where n is the unit vector which gives direction of the resultant vector.

Where a and b are the magnitudes of the vectors a and b respectively.

Question. Write down the difference between scalar and vector quantity.

Here are a few points which distinguish scalar and vector quantities.

Scalar Quantity:

To describe the quantity, only needs magnitude.
To add or subtract or to divide and multiply, we don’t need to develop any other algebra. The ordinary law of algebra is sufficient.
It is one dimensional only.
It is represented by single letter of alphabet only.
It may have positive, negative values.

Vector Quantity:

It refers to both magnitude and direction.
To add or subtract or to multiply, we need to use vector algebra.
It may have more than one dimension.
It is denoted by a single letter in bold faces, or by a single letter arrow on the head.
The magnitude of the quantity is given by the modulus of it.

Question. Give examples of scalar quantities.

Below is the list of some physical quantities which are scalar.

Temperature
Charge
Mass
Distance
Pressure
Density
Volume
Entropy
Resistance
Refractive index
Power
Surface energy
Strain

Question. Give examples of vector quantities?

Here are a few examples of the vector quantities.

Displacement
Force
Torque
Velocity
Momentum
Area
Acceleration
Magnetic field intensity
Electric field

Also Read:

TechieScience Core SME

The TechieScience Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the TechieScience.com website.

All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.