Fourier’s law | It’s All Important with 6 FAQs

by

Content

Fourier’s law of heat conduction        

Fourier’s law of conduction heat transfer can be states as below,

“The heat transfer rate passes from the material or specimen is directly proportional to the cross-sectional area (perpendicular area) from which heat is passing through, and temperature difference along the end surfaces of the material.”

Fourier's law
Fourier’s law of heat conduction

We can write this statement mathematically as,

q \\oe A \\frac{dT}{dx}

q = - K A \\frac{dT}{dx}

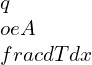
Where,

q = heat transfer rate in watt (W or J/s)

K = Thermal conductivity of material or specimen (W / m K)

A = Cross-sectional area from which the heat is passing through in m2

dT = Temperature  difference between the hot side and cold side in K ( Kelvin )

dx = Thickness of material in m (thickness between hot side to cold side)

Most important: Here in the equation, the negative sign indicates that the heat always flows in the direction of decreasing temperature.

Fourier’s law equation   

The equation of heat conduction law is as derived above. It is widely used to solve problems on heat conduction and analysis. The fundamental of the equation remains the same, but the parameters will be changed upon shape and situation of object.

q = - K A \\frac{dT}{dx}

Fourier’s law spherical coordinates  

The heat conduction law applied to cylinder and equation is given as below,

\\frac{1}{r^{2}}\\cdot \\frac{\\partial }{\\partial r}\\cdot \\left ( r^{2}K\\cdot \\frac{\\partial T}{\\partial r} \\right )+e_{gen}= \\rho c\\cdot \\frac{\\partial T}{\\partial t}

Here, at any location the area

A= 4\\Pi r^{2}

,

r is radius of considered cylindrical portion,

Cordinates
Rectangular, cylindrical and spherical coordinates Image Credit Book Cengel and Ghajar

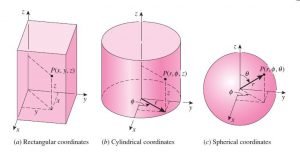
Fourier’s law cylindrical coordinates

The heat conuction law applied to cylinder and equation is given as below,

\\frac{1}{r}\\cdot \\frac{\\partial }{\\partial r}\\cdot \\left ( rK\\cdot \\frac{\\partial T}{\\partial r} \\right )+e_{gen}= \\rho c\\cdot \\frac{\\partial T}{\\partial t}

at any location the area A = 2πrL,

r is radius of considered cylindrical portion,

Fourier’s law experiment

Conduction heat transfer is occurred by microscopic diffusion and collisions of molecules or quasi-particles inside an object because of a temperature difference. If we see microscopically, then diffusing and colliding any material includes molecules, electrons, atoms.

Typically, metals have free electrons mobility inside an object. This is the reason behind its good conductivity.

Consider two-block A and B,

Block A is very hot

Block B is cold

block
Experiment for Fourier’s law of heat conduction

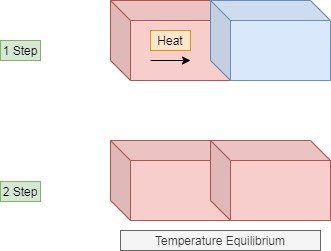
Suppose we join these two blocks and insulate all other outer surfaces. The insulation is provided to reduce surrounding heat loss from the block. You can quickly get the idea that the heat energy will flow from hot block to cold block. The heat transfer will continue until both of the blocks attain the same temperature (temperature equilibrium).

It is one of the method of heat transfer in both blocks. It is conduction heat transfer mode. Using the equation of heat conduction law, we can calculate the heat transfer with this experiment. It is very informative and important practical to be performed in heat transfer lab ( Mechanical engineering and Chemical engineering)

Fourier’s law history

Fourier started his work to express conduction heat transfer in 1822. He has also given the concept of Fourier series and Fourier integral. He was a mathematician. His law on conduction is well known on behalf of his name, “Fourier’s law of heat conduction.”

Fourier’s law units

Fourier’s law of heat conduction is stated for heat transfer. So, we can consider the unit of heat transfer for it. The unit of heat transfer is the watt ( J/s) W.            

Fourier’s law assumptions

There are some assumptions made for Fourier’s law of heat conduction. The law only applicable if following conditions will be followed and satisfied.

Fourier’s law of heat conduction example

There are many examples of law of heat conduction in day-to-day life. Some examples are discussed below.

There is hot coffee inside the mug. Now you know that heat will be transferred from the hot side to the cold side. Here, the heat transfer occurs from the inner wall to the outer wall of the mug. It is conduction heat transfer and based on Fourier’s law of heat conduction.

We can consider the wall of our house as for example.

If there is internal heat generation in the rod, heat will flow in the interior portion to outer surfaces.

You can touch any electrical and electronics equipment. You will get realize some heat. These all devices can be the example of Fourier’s law.                            

Fourier’s number

It is a dimensionless number derived by a non-dimensionalization heat conduction equation.

 Fourier’s number is denoted by Fo

F_{o} = \\frac{kt}{L^{2}}

Where,

L is plate length (Diameter in case of the cylinder) in m

K is the coefficient of gradient transport

T is time in s       

Fourier’s law flux

According to heat conduction law law,

The heat flux can be defined as the heat flow per unit area in unit time is directly proportional to the temperature difference between the hot and cold side (Temperature gradient.)

Heat flux

The heat flux can be defined as the heat flow per unit area in unit time is directly proportional to the temperature difference between the hot and cold side (Temperature gradient.)

Heat flux equation

The equation for heat flux is given as below,

q^{-} = - K\\frac{\\\\Delta T}{\\Delta X}

Where,

q- is heat flux in w / m2

K is thermal conductivity in w / m K

ΔT /ΔX is a temperature gradient,

Heat flux units

The unit of heat flux is   w / m2

FAQs   

What is Fourier’s law

                “The rate of heat transfer through the material or specimen is directly proportional to the cross-sectional area from which heat is passing through, and temperature difference along the end surfaces of the material.”

We can write this statement mathematically as,

q \\oe A \\frac{dT}{dx}

q = - K A \\frac{dT}{dx}

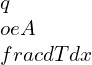
Where,

q = heat transfer rate in watt (W or J/s)

K = Thermal conductivity of material or specimen (W / m K)

A = Cross-sectional area from which the heat is passing through in m2

dT = Temperature  difference between the hot side and cold side in K ( Kelvin )

dx = Thickness of material in m (thickness between hot side to cold side)

Most important: Here in the equation, the negative sign indicates that the heat always flows in the direction of decreasing temperature.   

What are the assumptions of Fourier s law of heat conduction?

There are some assumptions made for Fourier’s law of heat conduction. The law only applicable if following conditions will be followed and satisfied. Fourier’s law of heat conduction can be compared with newton’s law of cooling and fick’s law of diffusion. The assumptions are different in every law.

  1. Conduction heat transfer will take place under steady-state conditions of an object.
  2. The flow of heat should be unidirectional.
  1. The temperature gradient will not be changed, and the temperature profile should be linear.
  2. The internal heat generation should be zero.
  3. The bounding surfaces should be adequately insulated.
  4. The material should be homogeneous and isotropic.

What is proof of the Fourier s law of heat conduction and the negative gradient?

The proof of Fourier’s law of heat conduction is already given in topic “Fourier’s law.”

The negative gradient is used because the heat always flows in decreasing temperatures. 

This question is very important for interview because interviewer always try to check your fundamental knowledge.          

How does Fourier’s law of heat conduction contradict the theory of relativity?

Fourier’s law contradicts the theory of relativity due to its instantaneous heat propagation through heat diffusion. If we consider time-dependent heat diffusion with a partial differential equation, The growth of heat flux will be with relaxation time. This time is in order of 10-11. Heat propagation takes infinite time in nature. The relaxation time is negligible.

If we eliminate relaxation time, then the equation becomes Fourier’s law of heat conduction. It is violating the popular theory of Einstein (theory of relativity). The velocity of light in a vacuum is 2.998 * 108

How is the physics behind Fourier’s law different from the one behind Newtons Law of cooling           

As we are already knowing, Fourier’s law is used for conduction heat transfer, and Newton’s law of cooling is used for convection heat transfer. Suppose you have a question that why two different laws are required for the heat transfer rate analysis. The reason behind it is modes of heat transfer are different from individual physics.

Conduction heat transfer is occurred by microscopic diffusion and collisions of molecules or quasi-particles inside an object because of a temperature difference. If we see microscopically, then diffusing and colliding any material includes molecules, electrons, atoms. They transfer kinetic and potential energy microscopically to each other. This energy is known as internal energy in the object. The law states conduction heat transfer is Fourier’s law.

Convection heat transfer in any object can be defined as heat transfer from one molecule to another by moving fluids or flow of fluid. Newton’s law of cooling defines convection heat transfer.

The physics used for the individual process is different. Hence, the governing law for an individual is different. 

What are the similarity between Newtons law of viscosity, Fourier’s law of heat conduction, and Fick’s law of diffusion?

It is the analogy between these equations.

Fourier’s law of Heat Conduction

It states the conduction heat transfer process. The equation can be written as below,

The equation for heat flux is given as below,

q^{-} = - K\\frac{\\\\Delta T}{\\Delta X}

Where,

q- is heat flux in w / m2

K is thermal conductivity in w / m K

ΔT /ΔX is a temperature gradient,

Fick’s law of Diffusion 

It is used to describe and state the mass transfer process. The equation for mass transfer can be written as below,

m^{-} = -D \\left ( \\frac{dC}{dX} \\right )

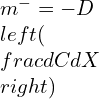
(dC/dx) is gradient of concentration

D is transport property diffusivity

Newton’s law of Viscosity 

It is used for momentum transfer and widely used to study viscosity of any fluid.

\\tau = -\\mu \\left ( \\frac{dU}{dX} \\right )

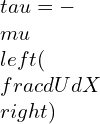
Here, (du/dx) is the velocity gradient

μ is the viscosity of fluid

Thus, you can analyze three different laws straight away about these equation’s relativity.

To read more articles to related topic please click here