Force on moving charge in electric field is determined when a charged particle moves without acceleration it produces an electric field.
Firstly an electric field is created when two parallel plates are charged, otherwise called capacitors. When the test charges are placed between the charged capacitor plates they move from the positive end to the negative end. Each such charge carries like this creating a line.
The test charges move from positive to negative side creating lines of force is called an electric field. Since these lines of charges form a uniform pattern, then there is said to be a uniform electric field created.
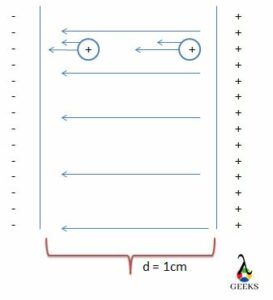
When a test charge is placed on the negative side of the plate, it will attract, and the force of attraction will be less. But when another test charge is placed closer to the positive side of the plate opposite to that of the other plate, the force of attraction would be more.
When the test charge is placed closer to the positive side of the charge, the repulsion is greater, and the force of attraction to the negative side of the plate is greater. So the force on a moving charge in an electric field depends on where the charge is situated and the distance.
Electric field is created only when the charges are at stationary. Therefore the force on that charge is determined based on the position of the test charge. Whether it is closer or far from the respective charges, it is placed.
How do you calculate the force of a moving charge
Force on moving charge in electric field is calculated using the formula is F = e E, here we consider the charge as electron and it is denoted by letter e. The electric field is denoted by letter E.
The force of the electron is nothing but the acceleration all over the mass of the electron in an electric field, and it is given as a = (e E) / m. This formula defines the electric field as the force by unit charge, E = F / q (e).
Now acceleration has been calculated, and the velocity goes like this, Vf2 = V02 + 2 a ∆ X. Where Vf is final velocity, and V0 is the initial velocity. The above formula is given in the assumption that the electron does not gain speed. This speed should not get too nearest to the light speed (3 X 108 m/s), or else it would become a whole different scenario. Hence the speed of the charge must be below.
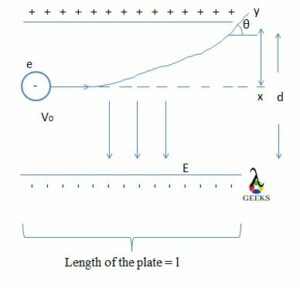
From the above picture, consider a negative test charge moving across electric fields. This charge has an initial velocity, and it will shoot up the electric field and not pass through it since two parallel plates have negative and positive charges on opposite sides.
When an electron with a negative charge is placed between the plates, it gets deflected by the charges present in the vicinity. Since the uniform electric field is produced in the process, the charge travels faster with the initial velocity and is also perpendicular to the field.
The charge experiencing a force when deflected by the electric field it will give a projectile. The electron will displace from its original place (x) to a new position called y. This forms a projectile path.
Now there are possibilities for the charge to move out of the plates. When this happens, it makes an angle θ with a projectile path. Here we must know what (y) is and θ is. The deflection comes from the image, (y), and θ is the electron’s angle emerges out of the plates.
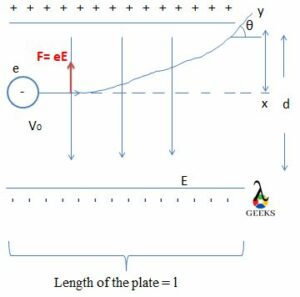
The electron placed between the plates experiences a force upwards because the side of the plate facing inward has a positive charge. Hence the electron will be attracted towards that side of the plate.
We need to calculate the force, acceleration, and velocity of the charge moving in the electric field. The force experienced by the moving charge in an electric field at point (y) is Fy = eE. Acceleration is ay = (eE) / m.
The deflection (y) is formulated, and finally, we get the equation to calcite the force is as follows (y) = (eE x2) / 2my2. Then the angle at which the electron emerges out of the charged capacitor plates is as given, tan θ = (eEx) / mV02 .
This is the basic formula we need to know before calculating the force on moving charges in the electric field. So, for now, we deal with simple techniques and so on.
Force on moving charge in electric field is the charge multiplied by the electric field or uniform electric field.
Force on a moving charge in a uniform electric field
We need to know that when a charge is in motion, it produces only a magnetic field. The charges which are not in motion produce electricity by default. Presence of an electric field causes magnetic field to be produced.
In a system, a point charge and a test charge is present. So the force exerted by the point charge on the test charge is called the electrostatic force. This is the force present on the moving charge in an electric field.
We can clearly understand how a force acts on a moving charge in an electric field using an example.
A charge travelling between the capacitor plates is attracted and repelled silmultaneously. When two plates are placed at a distance d the plates facing each other will have opposite charges.
So when a test charge is placed between, it will either get attracted or repelled depending on the magnitude it possesses.
Problems examples on Force On Moving Charge In Electric Field
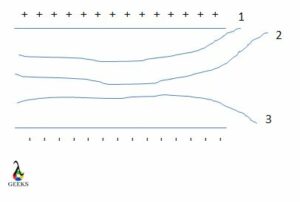
From the above-shown diagram, we must determine the sign or charge of the particle moving in a projectile motion. We know that 1, 2 travel in one direction and 3 travel in another direction.
Positively charged plate is placed on top, and the negatively charged plate below. Both the plates are faced inwards. And the charges are inwards.
Now the charges 1 and 2 travel towards the positive side of the plate, and charge 3 travel towards the negative side of the plate.
Charges 1 and 2 are negatively charged, and charge 3 is positively charged. This is a very simple way to find the sign of the charge moving in the electric field experiencing a force.
We will have to determine the charge to mass ratio, whether high or low, based on the direction in which each of these charges travels.
Charge 3 will have a charge-to-mass ratio very high due to the deflection being high. Meaning, that charge three is deflected to a long position from its original position. Since the deflection is high, the charge to mass ratio is also high.
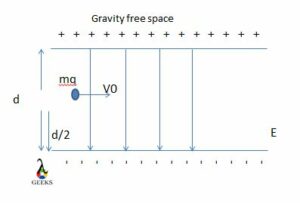
Consider two charged plates kept parallel to each other in a horizontal manner. Positively charged and negatively charged plates are placed top and bottom respectively. Length of the plate is l and the distance between the two plates is given by d
A charge mass m and charge +q are placed between the plates. This +q charge will be attracted to the lower plate. The electron has an initial velocity of V0. This velocity determines how far the charge will travel due to the presence of an electric field.
So now we need to find the minimum amount of initial velocity required to deflect more and just emerge out of the plates.
We know that the force is Fy = eE and acceleration is ay= (qE) / m. Using this information, a tedious calculation is made, and finally, we get the equation for calculating the minimum initial velocity. And that will be V0 = L {(qE / MD)}1/2.
Problem on force on a moving charge in a uniform electric field
Let us consider a charge moving in an electric field. The charge is placed between the charged capacitors. A force acts on the charge while in its motion. The electric field acting on a point charge q= 2 NC is E= 7.91 X 105 N/C. What force does the electric field exert on the charge?
F= eE
F = 2 X 10-9C X 7.19 X 105
F= 0.180N
Now we have a clear understanding of force acting on a moving charge in an electric field.
*************************
Also Read:
- Is static electricity a contact force
- How to find normal force with coefficient of friction
- Gravitational force of earth
- Internal forces examples
- Force of friction examples
- Central force examples
- Coriolis force example 2
- Electrostatic force and distance
- Can normal force be at an angle
- What objects have magnetic force
Hi…I am Keerthana Srikumar, currently pursuing Ph.D. in Physics and my area of specialization is nano-science. I completed my Bachelor’s and Master’s from Stella Maris College and Loyola College respectively. I have a keen interest in exploring my research skills and also have the ability to explain Physics topics in a simpler manner. Apart from academics I love to spend my time in music and reading books.
Let’s connect through LinkedIn