The drag is a force associated with the object in motion in a fluid environment. Drag force is specified by a dimensionless entity called drag coefficient, which helps describe the nature of the motion in the fluid.
The drag coefficient always defines the resistance offered to the object under motion in a fluid. Since the object under motion possesses a certain velocity, the drag coefficient and velocity are related. This post briefly explains the relationship between drag coefficient and velocity in various aspects.
Relation between drag coefficient and velocity
Drag coefficient CD is always defined using the terms such as density of the fluid, reference area of cross-section of the object, velocity, and the Reynolds number; thus, the relation between the drag coefficient and velocity can be written using the equation.
CD=2FD/v2Aρ
Where FD is the drag force, ρ is the mass density of the fluid; A is the reference area, and v is the relative velocity of the object in the fluid.
From the above expression, the relation between the drag coefficient CD and relative velocity v is given as
CD∝ 1/v2
The above expression means that a square increase in velocity decreases the drag coefficient. Thus drag coefficient and velocity are inversely related to each other.
Drag force and velocity relationship
The drag force always retards the flow of the object in the fluid. As the velocity increases, the drag force associated with it changes proportionally. The drag force acting on the object in a fluid is given by
FD=1/2 CDv2Aρ
From the above equation, in fluid mechanics, the relation between drag and velocity is explained by considering the object’s speed as low and high speed. The drag force varies differently for low and high speeds.
For low-speed flow, the drag force is proportional to the velocity given by
FD∝ v
For high-speed flow, the drag force is proportional to the square of the velocity given as
FD∝ v2
How does velocity affect drag?
The dependency of the drag on the square of the velocity is quite natural in the fluid dynamics, as the velocity shows some deviation in the drag when it changes.
The object floating in the fluid is associated with doubling velocity –this means as the velocity is increased to its square value, the drag increases by quadruple. The quadruple increase in the drag is due to other entities associated with the drag. The effect of velocity on drag is given by
D∝ v2
Thus we can write the above proportionality as
D=constant×v2
The constant in the above expression is regarded with the density, area, and drag coefficient associated with the drag.
Thus as the relative velocity increases to its square value, the drag increases by four times.
Drag force and angular velocity
Angular velocity is always associated with the rotating motion of the object. In order to describe drag force with the angular velocity, we have to consider linear drag expression; it is given below:
FD=1/2 CDv2Aρ
However, we are talking about rotational motion, the torque related to the drag force given as
τ ∝ rv2Aρ
Since the motion is rotational motion, thus the angular velocity of the object can be related to the linear velocity as
v=ω×r, where r is the radius of the rotational path and ω is the angular velocity associated with the rotating object.

Substituting the value of v, we get
τ ∝ r3 ω2Aρ
From the above expression, the drag force is equivalent to the torque acting on the rotating object.
Thus the drag force can be written as
FD=1/2 CDr3 ω2Aρ
Drag force and terminal velocity
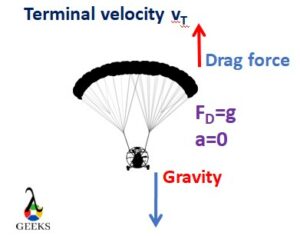
When an object falls freely from the fluid, the maximum velocity acquired by the object is called terminal velocity.
Consider an example of a skydiver; when he dives, he falls under the influence of gravity. There are two forces are acting on the diver, one is force of gravity, and another one is drag force. However, as the velocity of the diver increases, the magnitude of the drag force is also increased until it becomes equal to the magnitude of gravitational force.

As the magnitude of drag and gravitational force becomes equal, the net force acting on the diver is nullified, making the acceleration also zero. At this instance, the diver has attained the constant velocity called terminal velocity.
Relationship between drag force and terminal velocity
In the previous section, we have discussed the relation between the drag coefficient and velocity and drag force and angular velocity. Similarly the relation between the drag force and the terminal velocity can be given by considering the falling object.
As we know, when the object attains the terminal velocity, it experiences two forces, drag and gravitational force. The gravitational force can be given by as weight of the object. So the net force is given by
Fnet=W-FD, where W=mg
As the object attains terminal speed, the net force Fnet=ma=0
Thus FD=W=mg
Substituting the above equation we get
FD=1/2 CD VT2 Aρ
mg=1/2 CD VT2 Aρ
Rearranging the terms, we get terminal velocity as
vT2=2mg/CDAρ
vT=√2mg/CDAρ
What is drag force?
There is always a force of hindrance acting on the moving object, which offers resistance to the motion.
Drag force is exerted on the moving object in the fluid (liquid or gas). It can be defined as the force acting on the solid object moving in a fluid exerted opposite to the relative motion of the fluid.
Solved Problems On Drag force, Drag coefficient and Velocity
The drag force acting on a body is 235N, the density is given as 1.11kg/m3, and the cross-sectional area of the body is 2.33m2. The body’s drag coefficient is calculated as 0.14 hence calculating the body’s velocity.
Solution:
The drag force FD=235N
Density ρ=1.11kg/m3.
Cross-sectional are A=2.33m2
Drag coefficient CD=0.14
The velocity of the body
v=√2FD/CD Aρ
v= √2(235)/(0.14) * 1.11 Aρ
v=36.02m/s.
Calculate the drag force of an object rotating in a circular path of radius 3m in the air with a speed of 12m/s. The area of cross-section is 3.4m2, and the drag coefficient is 0.55.
Solution:
Drag coefficient CD=0.55
Radius of the path r=3m
Cross-sectional area A=3.4m2
Angular velocity ω=12m/s
Density of air ρ=1.21kg/m3
FD=1/2 CDr3 ω2Aρ
FD=1/2 * 0.55 * 33 * 122* 3.4* 1.21
FD=4.3×103N
A diver of mass 79kg is diving from the parachute. The drag coefficient of the diver is given as 0.73, and the area of the cross-section is considered as 0.17m2. Calculate the terminal velocity of the diver.
Solution:
Given –mass of the diver m=79kg
Drag coefficient CD=0.73
Area of cross-section A=0.17m2
From the above data, the terminal velocity can be given as
vT=√2mg/CD Aρ
The density of air ρ=1.21kg/m3
Acceleration due to gravity g=9.8m/s2
vT=√2(79*9.8)/0.73*0.17*1.21
vT=101.600m/s.
Also Read:
- How to find maximum velocity
- How to measure velocity in fusion physics
- Is angular velocity negative
- Initial velocity formula
- Orbital velocity of moon
- How to find velocity without time
- How to compute velocity in particle collisions
- How to find power with velocity and mass
- How to measure velocity using galilean relativity
- How to measure velocity in turbulent flow
I am Keerthi K Murthy, I have completed post graduation in Physics, with the specialization in the field of solid state physics. I have always consider physics as a fundamental subject which is connected to our daily life. Being a science student I enjoy exploring new things in physics. As a writer my goal is to reach the readers with the simplified manner through my articles.