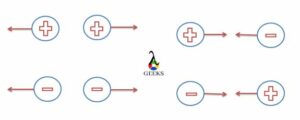
Resultant force is one single force replaced by multiple forces and equilibrium force is the balanced force where the net force acting is zero that is direct opposite to resultant force. Hence this is basic difference between resultant force and equilibrant force.
Resultant force is the sum of all individual forces acting on a body by vector determination. Resultant force can be zero if one force is opposite to the other combination. There are several forces acting on a body and they are dealt separately in terms of vertical and horizontal forces.
When the magnitude is the same and directions are opposites the forces cancel out each other we get a value of force which is the resultant force. For instance, 5N force on the left and 9N force on the right gives resultant force as 4N.
Resultant force examples
Let us have four forces acting on a system at the same time, 60N, 70N, 40N, -20N. The force 20N is negative because it is acting on the opposite direction to that of the others. Evaluate the resultant force.
FR = f1 + f2 + f3 + f4
FR = 60N + 70N + 40N – 20N
FR = 150N
Let two forces act perpendicular to each other, 9N and 4N. Determine the resultant force.
The formula for resultant force acting perpendicular to each other is
F = [(F1)2 + (F2)2]1/2
F = [(9)2 + (4)2]1/2
The resultant force or any other type of force can be explained easily using a free-body diagram. In this diagram we use arrows to indicate the magnitude and direction of the forces acting. The arrows pointing to a direction is the path of the force followed, and the length of the arrow shows specifies the magnitude.
While calculating the force present in the body, several forces come into play but resultant force gives value for the entire force present. Multiple forces acting on them goes balanced and unbalanced.
When the individual force have the same magnitude as the other they sum up also when the direction is the same then the system is said to have unbalanced force. But when the magnitude is the same and the direction is opposite to each other they cancel out each other and the system is said to have balanced force.
In a system there are several possible forces acting namely, normal force, frictional force, tensional force, gravitational force and so on. Resultant force is the final value of adding up these forces acting upon a body.
Equilibrant Force Concept
When the magnitude and the direction of the force acting on a body are balanced, showing zero net force and zero torque present in the system is known as the equilibrant force.
The state of balanced force occurs when a system in equilibrium. This happens when different forces acting upon the object are considered to be balanced.
The balancing of force in a system occurs when leftward force balances the rightward force and upward force balances the downward force.
Generally when the system is said to have balanced force, the individual forces cannot have the same value. For example, when a body is said to have balanced force, the individual force may differ and is explained using a free-body diagram.

Let’s consider a simple experiment to understand the concept of equilibrium force.
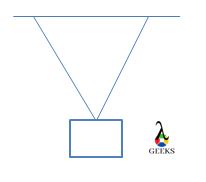
In physics lab, an object is suspended by two or more strings; force exerted is measured at angles made by the string with the object. Now the total number of forces acting on the object is measured.
If the object was to be in equilibrium the net force acting on the object should be of 0N. also, by adding up the force should be equal to zero.
Equilibrium Force Examples
Consider a man standing on the ground motionless. The forces acting on him will be zero since there is no acceleration and velocity. Due to this the man is said to be in static equilibrium.
Since the number of forces acting on the man is zero, and then the condition calls for equilibrium force in existence.

A car moves on a highway with constant acceleration and velocity. When it does not move the whole system stays motionless. The forces acting on the system is in each direction.

When children are seated on a see-saw, a rotating system, are said to be in equilibrium. If they are motionless and the forces acting on them becomes zero, by this way the torque becomes zero and it gives way for equilibrium force.

Therefore by all means, the total number of forces acting upon a body is balanced, making the net force zero, and the equilibrium force is achieved.
And when the entire force acting upon the object its magnitude and direction values are taken into account, by which on adding the resultant force is obtained.
Frequently asked Questions
Why does a force in equilibrium be zero?
In this condition two equal and opposite force exists balancing each other and the acceleration becomes zero.
The word equilibrium simply means balancing. In order for a system to be in equilibrium, there must be a balance of all the forces in the system and net force becomes zero.
When a net force does becomes zero in an equilibrium system?
The net force in a system becomes zero when all the forces acting in the system is balanced and when the acceleration turns to be zero.
This process occurs when all the forces in a system is balanced from all directions. Acceleration being zero the torque acting in a rotating system also becomes zero.
Will torque become zero if the net force is zero?
Torque is a cross product of distance and force, so when the net force is zero, torque will be zero.
If the displacement appears right after applying the force then the torque will be bigger than force. If displacement is missing even after the force application then force will be zero as well as the torque.
What is dynamic equilibrium?
Dynamic equilibrium is state of a system with motion and net force not equal to zero.
Dynamic equilibrium differs from static because dynamic mean the body is in motion with changing velocity and acceleration. The constant change in the acceleration velocity and torque (in rotating systems), is dynamic equilibrium.
**************************