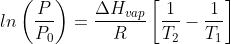Temperature

Diffusion and temperature are two closely related concepts in physics that play a crucial role in various physical and chemical processes. Understanding the intricate relationship between these two phenomena is essential for students studying physics, materials science, and related fields. This comprehensive guide will delve into the technical details, formulas, and practical applications of diffusion and temperature, providing a valuable resource for physics students.

Diffusion Coefficient: The Key to Understanding Diffusion

The diffusion coefficient is a fundamental parameter that describes the rate at which a substance spreads out in a given medium. This value can be measured in units of area per time, such as square centimeters per second (cm²/s). The diffusion coefficient is directly influenced by temperature, with higher temperatures generally leading to faster diffusion rates.

For example, in a study of diffusion in clay bricks, a diffusion coefficient of 0.014 cm²/s was measured at room temperature. This value is very close to the model prediction for the diffusion coefficient of sample A at an ambient temperature, which is 0.011 cm²/s. The diffusion coefficient can be calculated using the following formula:

D = (kB * T) / (6 * π * η * r)

Where:
– D is the diffusion coefficient (cm²/s)
– kB is the Boltzmann constant (1.38 × 10^-23 J/K)
– T is the absolute temperature (K)
– η is the dynamic viscosity of the medium (Pa·s)
– r is the radius of the diffusing particle (m)

This formula demonstrates the direct relationship between the diffusion coefficient and temperature, as the diffusion coefficient is proportional to the absolute temperature.

Mean Free Path Length and Knudsen Number

In addition to the diffusion coefficient, two other important parameters in the study of diffusion and temperature are the mean free path length (λ) and the Knudsen number (Kn).

The mean free path length is the average distance that a particle will travel before colliding with another particle. It can be calculated using the following formula:

λ = 1 / (√2 * π * d^2 * n)

Where:
– λ is the mean free path length (m)
– d is the diameter of the particles (m)
– n is the number density of the particles (m^-3)

The Knudsen number is the ratio of the mean free path length to the characteristic length scale of the system, and it is a dimensionless quantity. The Knudsen number can be calculated using the following formula:

Kn = λ / L

Where:
– Kn is the Knudsen number (dimensionless)
– λ is the mean free path length (m)
– L is the characteristic length scale of the system (m)

For example, in a study of gas diffusion in clay samples, the mean free path length and Knudsen number were calculated for nitrogen gas at various temperatures, using a mean pore diameter of 0.45 μm. The results showed that the Knudsen number was approximately equal to 1 over the entire temperature range studied, indicating that Knudsen diffusion was the dominant mechanism for gas diffusion in this system.

Temperature Dependency of Diffusion Coefficients

The temperature dependency of diffusion coefficients is often assumed to be exponential, with the diffusion coefficient increasing rapidly with temperature. This relationship can be described by the Arrhenius equation:

D = D0 * exp(-Ea / (R * T))

Where:
– D is the diffusion coefficient (cm²/s)
– D0 is the pre-exponential factor (cm²/s)
– Ea is the activation energy for diffusion (J/mol)
– R is the universal gas constant (8.314 J/mol·K)
– T is the absolute temperature (K)

The Arrhenius equation demonstrates that the diffusion coefficient is exponentially dependent on the inverse of the absolute temperature, with the activation energy (Ea) being a key parameter that determines the temperature sensitivity of the diffusion process.

However, it is important to note that the exact form of the temperature dependency can vary depending on the specific system and conditions being studied. In some cases, the relationship may not be strictly exponential, and other models or empirical correlations may be more appropriate.

Practical Applications of Diffusion and Temperature

The understanding of diffusion and temperature has numerous practical applications in various fields, including:

1. Materials Science: Diffusion plays a crucial role in the processing and properties of materials, such as the diffusion of dopants in semiconductor devices, the diffusion of atoms in metal alloys, and the diffusion of gases in porous materials.

2. Chemical Processes: Diffusion is a fundamental mechanism in many chemical processes, such as the transport of reactants and products in chemical reactions, the separation of gases in industrial processes, and the transport of ions in electrochemical systems.

3. Biological Systems: Diffusion is a vital process in biological systems, governing the transport of nutrients, gases, and other molecules across cell membranes and within living organisms.

4. Energy Storage and Conversion: Diffusion processes are important in energy storage and conversion technologies, such as the transport of ions in batteries and fuel cells, and the diffusion of gases in hydrogen storage materials.

5. Environmental Science: Diffusion plays a role in the transport and fate of pollutants in the environment, such as the diffusion of contaminants in soil and groundwater, and the diffusion of gases in the atmosphere.

By understanding the relationship between diffusion and temperature, students can gain valuable insights into these and other applications, and develop a deeper appreciation for the fundamental principles of physics.

Numerical Examples and Problem-Solving

To further solidify the understanding of diffusion and temperature, let’s consider some numerical examples and problem-solving exercises:

Example 1: Calculating the Diffusion Coefficient
Given:
– Temperature (T) = 298 K
– Dynamic viscosity of the medium (η) = 0.001 Pa·s
– Radius of the diffusing particle (r) = 1 × 10^-9 m

Calculate the diffusion coefficient using the formula:
D = (kB * T) / (6 * π * η * r)
D = (1.38 × 10^-23 J/K * 298 K) / (6 * π * 0.001 Pa·s * 1 × 10^-9 m)
D = 2.59 × 10^-10 m²/s

Example 2: Calculating the Mean Free Path Length and Knudsen Number
Given:
– Particle diameter (d) = 5 × 10^-10 m
– Number density of particles (n) = 1 × 10^28 m^-3
– Characteristic length scale of the system (L) = 1 × 10^-6 m

Calculate the mean free path length (λ) and the Knudsen number (Kn):
λ = 1 / (√2 * π * d^2 * n)
λ = 1 / (√2 * π * (5 × 10^-10 m)^2 * 1 × 10^28 m^-3)
λ = 6.93 × 10^-8 m

Kn = λ / L
Kn = (6.93 × 10^-8 m) / (1 × 10^-6 m)
Kn = 0.0693

These examples demonstrate how to apply the formulas and concepts discussed earlier to calculate the diffusion coefficient, mean free path length, and Knudsen number, which are essential for understanding the behavior of diffusion systems and their relationship with temperature.

Figures and Data Visualization

To further enhance the understanding of diffusion and temperature, it is helpful to incorporate relevant figures and data visualizations. For example, you could include:

1. Graph of Diffusion Coefficient vs. Temperature: This graph would demonstrate the exponential relationship between the diffusion coefficient and temperature, as described by the Arrhenius equation.

2. Plot of Mean Free Path Length vs. Temperature: This plot would show how the mean free path length varies with temperature, which is crucial for understanding the dominant diffusion mechanism in a given system.

3. Contour Plot of Knudsen Number vs. Temperature and Characteristic Length Scale: This plot would provide a visual representation of the Knudsen number as a function of both temperature and the characteristic length scale of the system, helping to identify the regions where Knudsen diffusion is the dominant mechanism.

4. Experimental Data Points and Comparison to Theoretical Models: Incorporating real-world experimental data points and comparing them to theoretical models would provide a more comprehensive understanding of the relationship between diffusion and temperature, and the limitations or assumptions of the models.

By incorporating these types of figures and data visualizations, you can create a more engaging and informative resource for physics students, helping them to better understand the concepts and apply them in practical situations.

Conclusion

In conclusion, the relationship between diffusion and temperature is a fundamental topic in physics that has numerous practical applications. By understanding the key parameters, such as the diffusion coefficient, mean free path length, and Knudsen number, as well as the temperature dependency of these values, students can gain a deeper appreciation for the underlying principles and their real-world implications.

This comprehensive guide has provided a detailed exploration of the technical aspects of diffusion and temperature, including relevant formulas, numerical examples, and data visualization. By mastering these concepts, physics students will be better equipped to tackle complex problems, design experiments, and contribute to the advancement of various fields that rely on the understanding of diffusion and temperature.

References

1. Instructables. “Real Diffusion Experiment for Home or School.” Instructables, www.instructables.com/Real-Diffusion-Experiment-for-Home-or-School/.
2. CliffsNotes. “Diffusion and Temperature.” CliffsNotes, www.cliffsnotes.com/study-notes/3784767.
3. Gao, Yonghui, et al. “Diffusion Coefficient Measurement and Modeling of Methane in Shale Rocks.” Processes, vol. 9, no. 8, 2021, p. 1400., doi:10.3390/pr9081400.
4. Cussler, E. L. “Diffusion: Mass Transfer in Fluid Systems.” Cambridge University Press, 1997.
5. Incropera, Frank P., et al. “Fundamentals of Heat and Mass Transfer.” John Wiley & Sons, 2007.

Melting point and temperature are fundamental concepts in physics and chemistry, particularly in the study of matter and its properties. The melting point is the temperature at which a solid substance transitions into a liquid state, while temperature is a measure of the average kinetic energy of a substance’s particles. Understanding these concepts is crucial for physics students to comprehend the behavior of materials and their phase changes.

Understanding Melting Point

The melting point of a substance is the temperature at which the solid and liquid phases of that substance are in equilibrium. This means that the rate of melting is equal to the rate of solidification at the melting point. The melting point is a characteristic property of a pure substance and is influenced by various factors, including the strength of intermolecular forces, the crystal structure, and the presence of impurities.

Factors Affecting Melting Point

1. Intermolecular Forces: The strength of intermolecular forces, such as van der Waals forces, hydrogen bonding, and ionic interactions, plays a crucial role in determining the melting point of a substance. Substances with stronger intermolecular forces generally have higher melting points.

2. Crystal Structure: The arrangement of atoms or molecules in the crystal structure of a solid substance can also affect its melting point. Substances with more complex and tightly packed crystal structures tend to have higher melting points.

3. Impurities: The presence of impurities in a substance can significantly affect its melting point. Impurities can disrupt the crystal structure and weaken the intermolecular forces, leading to a broader melting range and a lower observed melting point.

4. Pressure: The melting point of a substance can also be influenced by pressure. In general, an increase in pressure leads to an increase in the melting point, as the higher pressure makes it more difficult for the solid to transition into the liquid state.

Melting Point Determination Methods

There are several methods used to determine the melting point of a substance, each with its own advantages and limitations. Some of the most common methods include:

1. Capillary Tube Method: In this method, a small amount of the sample is placed in a thin, sealed glass capillary tube and heated at a controlled rate. The temperature at which the sample transitions from a solid to a liquid is recorded as the melting point.

2. Differential Scanning Calorimetry (DSC): DSC is a more advanced technique that measures the difference in heat flow between a sample and a reference material as a function of temperature. This method can provide detailed information about the melting point, as well as other thermal properties of the sample.

3. Melting Point Apparatus: Specialized melting point apparatuses are designed to precisely control the heating rate and monitor the temperature at which the sample transitions from solid to liquid.

4. Thermomicroscopy: This method combines a microscope with a heating stage to visually observe the melting process of a sample. It allows for the observation of the melting range and the identification of any phase changes.

Understanding Temperature

Temperature is a measure of the average kinetic energy of the particles (atoms or molecules) in a substance. It is a fundamental quantity in physics and is used to describe the thermal state of a system. The concept of temperature is closely related to the concept of heat, which is the transfer of energy due to a temperature difference.

Temperature Scales

There are several temperature scales used in physics and chemistry, each with its own advantages and applications. The most common temperature scales are:

1. Celsius (°C): The Celsius scale is widely used in scientific and everyday applications. It is defined such that the freezing point of water is 0°C and the boiling point of water is 100°C at standard atmospheric pressure.

2. Fahrenheit (°F): The Fahrenheit scale is primarily used in the United States and a few other countries. The freezing point of water is defined as 32°F, and the boiling point of water is 212°F.

3. Kelvin (K): The Kelvin scale is the base unit of temperature in the International System of Units (SI). It is defined such that the absolute zero (the lowest possible temperature) is 0 K, and the freezing point of water is 273.15 K.

Measuring Temperature

Temperature can be measured using various types of thermometers, each designed to work within a specific temperature range and with varying degrees of accuracy. Some common temperature measurement devices include:

1. Liquid-in-Glass Thermometers: These thermometers use the expansion and contraction of a liquid, such as mercury or alcohol, to indicate the temperature.

2. Bimetallic Thermometers: These thermometers rely on the differential expansion of two different metals to measure temperature changes.

3. Thermocouple Thermometers: Thermocouples generate a small electrical voltage that is proportional to the temperature difference between the two junctions of the thermocouple.

4. Resistance Temperature Detectors (RTDs): RTDs measure the change in electrical resistance of a metal, such as platinum, as a function of temperature.

5. Infrared Thermometers: These non-contact thermometers measure the infrared radiation emitted by an object to determine its surface temperature.

Melting Point and Temperature in Physics

The concepts of melting point and temperature are fundamental in various areas of physics, including thermodynamics, phase transitions, and material science.

Thermodynamics and Phase Transitions

In thermodynamics, the melting point is the temperature at which the Gibbs free energy of the solid and liquid phases are equal, indicating the point of phase transition. The study of phase transitions, such as the solid-liquid and liquid-gas transitions, is crucial for understanding the behavior of materials and the energy changes involved in these processes.

Latent Heat and Phase Changes

During a phase change, such as melting or boiling, the temperature of the substance remains constant until the phase transition is complete. This is due to the latent heat of the phase change, which is the energy required to overcome the intermolecular forces and change the state of the substance. The latent heat of melting is the energy required to transition a substance from the solid to the liquid state.

Material Science and Crystal Structure

The melting point of a substance is closely related to its crystal structure and the strength of the intermolecular forces. Understanding the relationship between melting point, crystal structure, and material properties is essential in materials science, where researchers study the behavior and applications of various materials.

Numerical Examples and Problems

1. Melting Point of Water: The melting point of pure water at standard atmospheric pressure is 0°C or 273.15 K.

2. Melting Point of Copper: The melting point of pure copper is 1,084.62°C or 1,357.77 K.

3. Effect of Pressure on Melting Point: The melting point of ice increases by approximately 0.0075°C per atmosphere of increased pressure.

4. Latent Heat of Melting: The latent heat of melting for water is 334 kJ/kg, meaning that 334 kJ of energy is required to melt 1 kg of ice at 0°C.

5. Melting Point Depression: The melting point of a substance can be lowered by the addition of impurities. For example, the melting point of water decreases by approximately 1.86°C for every 1 molal (mol/kg) of solute added.

These examples and problems demonstrate the practical applications of melting point and temperature in various areas of physics, such as thermodynamics, phase transitions, and material science.

Conclusion

Melting point and temperature are fundamental concepts in physics and chemistry that are crucial for understanding the behavior of materials and their phase changes. By mastering these concepts, physics students can gain a deeper understanding of thermodynamics, phase transitions, and material properties, which are essential for their academic and professional development.

References

1. Atkins, P., & de Paula, J. (2014). Atkins’ Physical Chemistry (10th ed.). Oxford University Press.
2. Callister, W. D., & Rethwisch, D. G. (2020). Materials Science and Engineering: An Introduction (10th ed.). Wiley.
3. Cengel, Y. A., & Boles, M. A. (2015). Thermodynamics: An Engineering Approach (8th ed.). McGraw-Hill Education.
4. Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers with Modern Physics (10th ed.). Cengage Learning.
5. Tipler, P. A., & Mosca, G. (2008). Physics for Scientists and Engineers (6th ed.). W. H. Freeman.

The dew point temperature is a crucial parameter in understanding the relationship between air temperature and moisture content. Contrary to popular belief, the dew point temperature is not directly dependent on the air temperature. Instead, it is influenced by a complex interplay of factors, including atmospheric pressure, humidity, and the presence of condensation nuclei.

Understanding Dew Point Temperature

Dew point temperature is the temperature at which the air becomes saturated with water vapor, and any further cooling will result in the formation of dew or other forms of condensation. It is a direct measure of the amount of moisture present in the air, and is often used in various applications where the presence of moisture can cause problems, such as in industrial processes or the storage of perishable goods.

Factors Affecting Dew Point Temperature

The dew point temperature is influenced by several factors, including:

1. Atmospheric Pressure: The dew point temperature is inversely related to atmospheric pressure. Higher pressure results in a lower dew point temperature, while lower pressure leads to a higher dew point temperature.

2. Humidity: The amount of water vapor present in the air directly affects the dew point temperature. Higher humidity levels correspond to a higher dew point temperature, and vice versa.

3. Condensation Nuclei: The presence of tiny particles, such as dust or smoke, in the air can act as condensation nuclei, facilitating the formation of dew or other forms of condensation at a higher temperature than would otherwise be possible.

Relationship between Temperature and Dew Point

The relationship between air temperature and dew point temperature is complex and can be influenced by various factors. In general, as the air temperature increases, the amount of moisture the air can hold also increases. However, this does not necessarily mean that the dew point temperature will also increase.

In fact, in some cases, the dew point temperature may actually decrease as the temperature increases, particularly if the atmospheric pressure is also increasing. This is because the increase in temperature can lead to a decrease in the relative humidity, which can offset the increase in the absolute amount of moisture the air can hold.

Measuring Dew Point Temperature

There are several methods used to measure the dew point temperature, including:

1. Psychrometers: These instruments use the difference in temperature between a dry-bulb thermometer and a wet-bulb thermometer to calculate the dew point temperature.

2. Dew Point Hygrometers: These devices directly measure the dew point temperature by cooling a surface until condensation forms, and then measuring the temperature of the surface at the point of condensation.

3. Chilled Mirror Hygrometers: These instruments work by cooling a mirror until condensation forms on the surface, and then measuring the temperature of the mirror at the point of condensation.

Practical Applications of Dew Point Temperature

The dew point temperature is an important parameter in various applications, including:

1. Industrial Processes: In industries where the presence of moisture can cause problems, such as in the production of electronics or the storage of sensitive materials, the dew point temperature is closely monitored to ensure optimal conditions.

2. HVAC Systems: The dew point temperature is used in the design and operation of heating, ventilation, and air conditioning (HVAC) systems to prevent the formation of condensation and ensure comfortable indoor environments.

3. Weather Forecasting: Dew point temperature is a key factor in weather forecasting, as it helps predict the likelihood of precipitation, fog, and other weather phenomena.

4. Agriculture: Farmers and horticulturists use dew point temperature to assess the risk of plant diseases and optimize irrigation and pest control strategies.

Numerical Examples and Calculations

To illustrate the relationship between temperature and dew point, let’s consider a few numerical examples:

1. Example 1: Suppose the air temperature is 25°C (77°F) and the relative humidity is 60%. Using the Clausius-Clapeyron equation, the dew point temperature can be calculated as approximately 17°C (63°F).

2. Example 2: If the air temperature increases to 30°C (86°F) while the relative humidity remains at 60%, the dew point temperature would decrease to approximately 16°C (61°F). This is because the increase in temperature leads to a decrease in relative humidity, which offsets the increase in the absolute amount of moisture the air can hold.

3. Example 3: Suppose the air temperature is 20°C (68°F) and the atmospheric pressure is 1 atm. If the pressure increases to 1.1 atm, the dew point temperature would decrease from approximately 14°C (57°F) to 12°C (54°F), demonstrating the inverse relationship between pressure and dew point temperature.

These examples illustrate the complex and non-linear relationship between air temperature and dew point temperature, and the importance of considering other factors, such as humidity and atmospheric pressure, when analyzing this relationship.

Conclusion

In summary, the dew point temperature is not directly dependent on the air temperature, but rather is influenced by a variety of factors, including atmospheric pressure, humidity, and the presence of condensation nuclei. While the air temperature can influence the amount of moisture the air can hold, the dew point temperature may not necessarily increase with increasing temperature, as other factors can play a significant role in determining its value. Understanding the relationship between temperature and dew point is crucial in various applications, from industrial processes to weather forecasting and agriculture.

References:

1. Dew point temperature – What does it mean and how can it be calculated? (n.d.). Retrieved June 24, 2024, from https://www.vaisala.com/en/expert-article/dew-point-temperature-what-does-it-mean-and-how-can-it-be-calculated
2. Understanding Dew Point Temperature – GreenBuildingAdvisor (n.d.). Retrieved June 24, 2024, from https://www.greenbuildingadvisor.com/article/understanding-dew-point-temperature
3. The relationship of atmospheric air temperature and dew point temperature (n.d.). Retrieved June 24, 2024, from https://iopscience.iop.org/article/10.1088/1748-9326/ab2a26
4. Dew Point Definition and How to Measure It for Industries (n.d.). Retrieved June 24, 2024, from https://www.processsensing.com/en-us/blog/dew-point-definition-and-how-to-measure-it-for-industries.htm
5. What is humidity and the dew point? (n.d.). Retrieved June 24, 2024, from https://www.13newsnow.com/article/weather/what-is-the-dew-point/291-a5b83fad-6fdd-4481-88b8-a321cf548bca