Negative - lambdageeks.com

What Is Negative Magnification: Detailed Insight And Facts

January 20, 2024February 3, 2022 by Rabiya Khalid

In optics, the comparative size of an image with the object is termed magnification. Let us know what is negative magnification.

The magnification tells us the size of an image, whether it has increased or decreased. Apart from size, the magnification also represents the nature of the image. The positive magnification is for virtual images, whereas the negative magnification is for real images.

Optics is the study of light and image formation through mirrors and lenses. You can find two types of a mirror as well as a lens; one concave and the other convex.

As per the rules of image formation of the mirror, the images through concave and convex mirrors are formed. For the mirror, the magnification formula is given as:

m = h’/h = -v/u

Here,

m represents the magnification that is produced by the mirror

h’ is the height of the image

h is the height of the object

v is the image distance

u is the object distance

Similarly, for the lens, the formula of magnification becomes:

m = h’/h = v/u

The images formed by lens or mirror are either real or virtual images. In simple language, the real images are this which can be obtained on any type of screen, and this property is not found with virtual images.

Now let us know what is negative magnification in detail and all the facts.

250px Reflection and refraction.svg 1 — Image Credit: Epzcaw, Reflection and refraction, CC BY-SA 3.0

What is positive and negative magnification?

The magnification tells us to what extent the size of the image has increased or decreased. If the magnitude of the magnification is 1, then it indicates that the image size is the same as the object’s size.

If the magnitude of magnification is below 1, then the size of the image has diminished as compared to the object. At the same time, the magnitude of magnification above 1 means that the size of the image has increased when compared to the object.

Apart from the size, the magnification also tells about the nature of the image, i.e., real image or virtual image.

According to sign convention, the object and the image above the optic axis are taken as positive, i.e. erect. On the other hand, the image formed below the optic axis is taken as negative that is inverted.

Now using the magnification that is m = h’/h we can know the sign of the image formed. The object is always placed in an erect position that is its sign is always positive. So the sign of magnification tells as the sign of image. If m is positive, then it infers that the image is erect, and as we know, erect images are always virtual. The negative magnification is used to represent the real and inverted image. An inverted image is always real.

So now we know that positive magnification means virtual and erect images. Negative magnification indicates real and inverted.

In which lens magnification is negative?

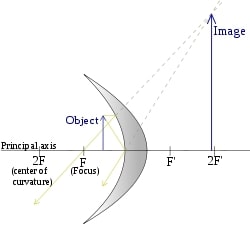
The convex mirror can produce both negative magnification and positive magnification. But the concave lens always has a positive magnification; that is, it is always virtual and erect. Let’s take one image formation of a convex lens to understand what is negative magnification.

What is negative magnification — Image Credit: By w:en:DrBob – w:en:File:Lens3.svg, GFDL, https://commons.wikimedia.org/w/index.php?curid=9690292

We have a convex lens, as shown in the above figure. We kept the object between in front of the mirror. Now we draw two light rays, one parallel to the principal axis.. The second ray passes through optical center O and refracts back on the same path. In the figure, we can see that after refraction the rays converge and meet behind the lens. The image that is formed is inverted, which means that it is real in nature.

Now let us take the height of the object as 10 cm; therefore, the image formed is -8 cm. Therefore the magnification becomes:

m =h’/h

m = -8/10, which is negative.

What does negative magnification indicate?

The magnification can be positive or negative. The negative sign of the magnification infers that the image formed by the mirror or lens is real. And it is formed below the principal axis, i.e., it is inverted.

When the rays of the object converge and meet actually then the image is formed, which is real in nature. They can be obtained on a screen at the point where the rays meet. The images formed on the screen of a cinema are real images that the magnification produced is negative.

Why is magnification of the mirror negative for real images?

The negative magnification of the mirror is for real images as they are always produced inverted.

The magnification produced by the mirror is given by the formula:

m = h’/h

Here,

h’ is the size of the image, and h is the size of the object.

The object is placed above the principal axis, which is why its size is taken positive. And therefore, the sign of magnification is due to the height of the image, i.e., he. Since real images are always produced inverted, and thus they have negative heights. Therefore negative magnification is for real images.

If we see the formulam = -v/u. The distance of the object has a negative sign, and the image here too has a negative sign. Therefore magnification for real images become:

m = -(-v/-u)

m = -v/u

Can a convex mirror have a negative magnification?

The convex mirror, also known as a diverging mirror, only forms a virtual image. At the same time, the concave mirror can form both virtual and real images.

Virtual images in the mirror are formed behind the mirror so that according to sign convention, the image distance is positive. We take the sign of the distance of the object kept in front of a mirror as negative.

Therefore from the magnification formula for the image formed by a convex mirror we get:

m = -v/u

m = -v/-u

m =v/u

That is, magnification produced by a convex mirror is always positive, and hence a convex mirror can never have a negative magnification.

When magnification is negative in a concave mirror?

The concave mirror usually produces real and inverted images. That is, the magnification is generally negative. But the concave mirror can also produce a virtual image in one case, then magnification is positive.

We take the concave mirror, as shown in the above ray diagram. Now we keep the object between the focus f and the pole, P. Two rays are drawn, one traveling parallel that after reflection passes through the center and the other one through the center of Curvature, C that deflects back on the same path. The two reflected rays meet behind the mirror after producing it further.

According to sign convention, we have object distance as -u and image distance as -v. Therefore, magnification becomes:

m = -(-v/-u)

m = -v/u

Does negative magnification mean smaller images?

No, the sign of magnification is related to the nature of the image, not its size. The negative magnification infers the image is real and inverted, and similarly, the positive magnification indicates virtual and erect.

Magnification is used to represent the size of the image formed. The magnification of magnitude 1 means that the image formed is of equal size as that of the object. In case the magnitude is greater than 1, then the size of the image has increased. Whereas a magnitude less than 1 indicates a small image.

What is the magnification of the convex mirror?

The concave mirror produces a real image. However, in one case, the image becomes virtual, and hence the magnification becomes positive. Whereas for the convex mirror, the magnification is always positive.

The reason is that the convex mirror can never produce real images. They can form virtual and erect images. The virtual image is depicted by the positive magnification. Therefore a convex mirror has positive magnification.

Frequently Asked Questions (FAQs)

How is a real image different from a virtual image?

The images are formed by mirrors and lenses. The images can be real or inverted.

The real images are those images that can be obtained on the screen and are inverted. At the same time, the virtual images cannot be obtained on the screen and are erect.

What is magnification?

In optics, we calculate the magnification to know about the size of the image formed.

The magnification gives the comparative size of the image concerning the object. If magnification is greater than 1, then the image is magnified. If less than 1, then the image has diminished. When the magnitude of magnification is 1, then the size of the image and object is found to be the same.

What is negative magnification?

The magnification of the mirror or lens also tells about the name of the image. The negative magnification is used to represent real images. Real images are those types that can be achieved on a screen.

Which mirror produces negative magnification?

Real and inverted images are represented by negative magnification.

The images formed by concave mirrors are generally real and inverted. The convex mirror produces images virtual images. Hence its magnification is always positive and never negative.

Also Read:

Exploring the Intricacies of Negative Frequency: A Comprehensive Guide

June 18, 2024October 7, 2021 by Esha Chakraborty

Negative frequency is a fundamental concept in signal processing and Fourier analysis, providing a mathematical framework for describing signals that oscillate or vary in a direction opposite to what might be expected. While not a directly measurable quantity, negative frequency can be related to various measurable quantities, offering valuable insights into the nature of signals and the analysis of qualitative data.

Understanding Negative Frequency

Negative frequency arises in the context of the Fourier transform, a powerful mathematical tool used to analyze signals in the frequency domain. In this domain, negative frequencies correspond to complex exponential signals with negative frequencies in radians per second. These negative frequencies can be related to the positive frequencies through the use of complex exponentials, which are mathematically linked to real-valued cosine and sine functions.

Relationship between Positive and Negative Frequencies

The relationship between positive and negative frequencies can be expressed mathematically using the following equation:

x(t) = A cos(2πft + φ) = A/2 * (e^(i2πft + iφ) + e^(-i2πft - iφ))

where:
– x(t) is the time-domain signal
– A is the amplitude of the signal
– f is the frequency of the signal
– φ is the phase of the signal
– i is the imaginary unit (√(-1))

The second part of the equation shows how the cosine function can be expressed as the sum of two complex exponential functions, one with a positive frequency and one with a negative frequency. This relationship is crucial in understanding the role of negative frequencies in signal processing.

Negative Frequencies in the Frequency Domain

In the frequency domain, negative frequencies correspond to complex exponential signals with negative frequencies in radians per second. These negative frequencies can be related to the positive frequencies through the use of complex exponentials, as shown in the equation above.

The Fourier transform, which converts a time-domain signal into the frequency domain, can be expressed as:

X(f) = ∫ x(t) e^(-i2πft) dt

where X(f) is the Fourier transform of the signal x(t). The negative frequency component of the Fourier transform corresponds to the second term in the equation for the cosine function, where the frequency is negative.

Practical Applications of Negative Frequency

While negative frequency itself is not a directly measurable quantity, it can be related to various measurable quantities in the context of signal processing and data visualization.

Signal Processing Applications

In the context of signal processing, negative frequencies can be used to describe the behavior of certain types of signals, such as:

Cosine Signals: The frequency of a cosine signal can be positive or negative, corresponding to the direction of oscillation.
Modulated Signals: In amplitude modulation (AM) and frequency modulation (FM) techniques, the modulated signal can be represented as the sum of positive and negative frequency components.
Analytic Signals: Analytic signals, which are complex-valued functions, can be used to represent the positive and negative frequency components of a real-valued signal.

Understanding the role of negative frequencies in these signal processing applications can provide valuable insights into the behavior and characteristics of the signals being analyzed.

Data Visualization Applications

Negative frequencies can also be related to measurable quantities in the context of data visualization. For example, in a sunburst graphic that illustrates the relationship between different units of qualitative analysis, the relative frequency or percentage of a concept can be represented by the amount of space taken up by the “slice” of the donut or pie.

This representation can be useful for showing the layers of meaning contained in the qualitative data, including any nuances that may be present in open-ended responses. By relating the relative frequency or percentage of a concept to the negative frequency component of the data, researchers and analysts can gain a deeper understanding of the underlying patterns and relationships within the data.

Advanced Concepts in Negative Frequency

Beyond the basic understanding of negative frequency, there are several advanced concepts and techniques that can be explored to deepen one’s understanding of this topic.

Negative Frequency in Quantum Mechanics

In the field of quantum mechanics, negative frequency is closely related to the concept of negative energy states. According to the Dirac equation, which describes the behavior of relativistic electrons, the solutions to the equation include both positive and negative energy states.

The negative energy states correspond to the existence of anti-particles, such as the positron, which is the anti-particle of the electron. The relationship between negative frequency and negative energy states in quantum mechanics is a complex and fascinating topic that has important implications for our understanding of the fundamental nature of reality.

Negative Frequency in Optics and Electromagnetics

In the field of optics and electromagnetics, negative frequency can be related to the concept of negative refractive index materials. These materials, also known as metamaterials, exhibit a negative refractive index, which means that the direction of the propagation of light or electromagnetic waves is opposite to the direction of the energy flow.

The negative refractive index can be related to the negative frequency component of the electromagnetic waves, and this phenomenon has important applications in the design of specialized optical devices and antennas.

Numerical Simulations and Modeling

Negative frequency can also be an important consideration in numerical simulations and modeling of various physical systems. For example, in the simulation of electromagnetic wave propagation, the inclusion of negative frequency components can be crucial for accurately capturing the behavior of the system.

Numerical techniques, such as the Finite Difference Time Domain (FDTD) method, can be used to model the propagation of electromagnetic waves, including the negative frequency components. These simulations can provide valuable insights into the behavior of complex systems and can be used to design and optimize various engineering applications.

Conclusion

By understanding the relationship between positive and negative frequencies, the role of negative frequencies in the frequency domain, and the practical applications of negative frequency in signal processing and data visualization, researchers and analysts can gain a deeper understanding of the signals and data they are working with. Additionally, the advanced concepts of negative frequency in quantum mechanics, optics and electromagnetics, and numerical simulations and modeling, provide further opportunities for exploration and discovery in this fascinating field of study.

References:
– Negative Frequency in Signal Processing
– Quantifying Qualitative Data with Data Visualization
– Understanding Negative Frequencies
– Techniques for Analyzing Open-Ended Survey Responses
– Negative Refractive Index and Metamaterials
– Finite Difference Time Domain (FDTD) Method