Permutation And Combination: 7 Complete Quick Facts

Properties of Permutation and combination

  When discussing permutation and combination as we are dealing with selection and arrangement with or without order considerations, depending on the situation there are different types and properties for the permutation and combination, these differences among permutations and combinations we will explain here with justified examples.

permutations without repetition

  This is the normal permutation which arranges n objects taken r at a time i.e nPr

ⁿ P_r=n!/(n-r)!

number of orderings of n different objects taken all at a time ⁿ P_n =n!

In addition, we have

ⁿP₀ = n!/n!=1

ⁿP_r = n.^n-1P_r-1

0!=1

1/(-r)!= 0 or (-r)!=∞

permutations with repetition

 Number of permutations (arrangements) for different items, taken r at a time, where each item can happen once, twice, three times, …….. r-times as many in any arrangement = Number of ways to fill r areas where each item can be filled with any of the n items.

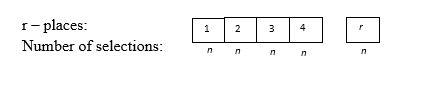
The number of permutations = The number of ways of filling r places = (n)^r

The number of orders that can be organized using n objects out of which p are alike (and of one kind) q are alike (and of another kind), r are similar (and of another kind) and the rest are distinct is ⁿP_r =n!/(p!q!r!)

Example:

In how many ways can 5 apples be allocated among four boys when every boy can take one or more apples.      

Solution: This is the example of permutation with repetition as we know that for such cases we have

The number of permutations = The number of ways of filling r places =n^r

Required number of ways are 4⁵ =10, Since each apple can be distributed in 4 ways.

Example: Find the number of words can be organized with the letters of the word MATHEMATICS by regrouping them.

Solution: Here we can observe that there are 2 M’s, 2 A’s and 2T’s this is the example of permutation with repetition

=n!/(p!q!r!)

 Required number of ways are =11!/(2!2!2!)=4989600

Example: How many ways in which the number of tails equal to the number of heads if six identical coins are arranged in a row.

Solution: Here we can observe that

No. of heads=3

No. of tails =3

And since coins are identical this is the example of permutation with repetition =n!/(p!q!r!)

Required number of ways =6!/(3!3!)= 720/(6X6)=20

Circular permutation:

In circular permutation, most importantly the ordering of the object is respect to the others.

So, in circular permutation, we adjust the position of one object and arrange the other objects in all directions.

Circular permutation is split into two ways:

(i) Circular permutation where clockwise and anti-clockwise settings suggest different permutation, e.g. Arrangements for seating people around the table.

(ii) Circular permutation where clockwise and anti-clockwise settings display same permutation, e.g. arranging certain beads to create a necklace.

Clockwise and anti-clockwise arrangement

If the anti-clockwise and clockwise order and movement are not different eg, bead arrangement in necklace, flower arrangement in garland etc, then the number of circular permutations of n distinct items is (n-1)!/2

1. The number of circular permutation for n different items, taken r at a time, when the orders for the clockwise and the anti-clockwise  are considered to be different by ⁿP_r /r
2. The number of circular permutation for n different items, taken r at a time, when clockwise and anti-clockwise orders are not different from ⁿP_r /2r
3. The number of circular permutations of n different objects are (n-1)!
4. The number of ways in which n different boys can be seated round a circular table is (n-1)!
5. The number of ways in which n different gems can be set up to form a necklet, is (n-1)!/2

Example:

How many ways can five keys be placed in the ring

Solution:

Since clockwise and anticlockwise are same in case of ring.

If the anti-clockwise and clockwise sequence and movement are not different then the number of circular permutations of n distinct items is

=(n-1)!/2

Required number of ways = (5-1)!/2= 4!/2=12     

Example:

What would be the number of arrangements, If eleven members of a committee sit at a round table so that the President and Secretary always sit together.

Solution:

By fundamental property of circular permutation

The count of circular permutations of n different things are (n-1)!

Since two positions are fix so we have

Required number of ways (11-2)!*2=9!*2=725760

Example: What would be number of ways 6 men and 5 women can eat at a round table if no two women can sit together

Solution: By fundamental property of circular permutation.

The count of circular permutations of n different things are (n-1)!

Number of ways in which 6 men can be arranged at a round table = (6 – 1)!  =5!

Now women can be arranged in 6! ways and Total Number of ways = 6! × 5!

Combinations without repetition

This is the usual Combination which is “The number of combinations (selections or groups) that can be formed from n different objects taken r at at a time is ⁿC_r =n!/(n-r)!r!

Also    ⁿC_r =ⁿC_r-r

              ⁿ P_r /r! =n!/(n-r)! =ⁿC_r

Example: Find the number of options to fill 12 vacancies if there are 25 candidates and five of them are from the scheduled category, provided that 3 vacancies are reserved for the S.C candidates mean while the remaining are open to everyone.

Solution: Since 3 vacant positions are filled from 5 applicants in ⁵ C₃  ways (i.e 5 CHOOSE 3) and now remaining candidates are 22 and remaining seats are 9 so it would be ²²C₉ (22 CHOOSE 9) The selection can be made in ⁵ C₃  X ²²C₉ ={5!/3!(5-3)! }X{22!/9!(22-9)!}

⁵ C₃  X ²²C₉ = {(3!X4X5)/(3!X2!)}X {22!/(9!X13!)}=4974200

So the selection can be made in 4974200 ways. 

Example: There are 10 candidates and three vacancies in the election. in how many ways a voter can cast his or her vote?

Solution: Since there are only 3 vacancies for 10 candidates so this is the problem of 10 CHOOSE 1, 10 CHOOSE 2, and 10 CHOOSE 3 Examples,

A voter can vote in ¹⁰C₁+¹⁰C₂+¹⁰C₃ = {10!/1!(10-1)!}+{10!/2!(10-2)!}+{10!/3!(10-3)!} =10+45+120= 175 ways.

 So in 175 ways voter can vote.

Example:There are 9 chairs in a room for 4 people, one of which is a single-seat guest with one specific chair. How many ways can they sit?

Solution: Since 3 chairs can be select in ⁸C₃ and then 3 persons can be arranged in 3! ways.

3 persons are to be seated on 8 chairs ⁸C₃ (i.e 8 CHOOSE 3) arrangement

=⁸C₃ X3! = {8! /3!(8-3)!} X3!

=56X6=336

In 336 ways they can sit.

Example: For five men and 4 women, a group of 6 will be formed. In how many ways this can be done so that the group has more men.

Solution: Here the problem include different combinations like 5 CHOOSE 5, 5 CHOOSE 4, 5 CHOOSE 3 for men and for women it include 4 CHOOSE 1, 4 CHOOSE 2 and 4 CHOOSE 3 as given in the followings

1 woman and 5 men =⁴C₁ X ⁵C₅ ={4!/1!(4-1)!} X{5!/5!(5-5)!}=4

           2 women and 4 men =⁴C₂ X ⁵C₄ = {4!/2!(4-2)!} X{5!/4!(5-4)!}=30

           3 women and 3 men =⁴C₃ X ⁵C₃ = {4!/3!(4-3)!} X {5!/3!(5-3)!} =40

    Hence total ways = 4+30+40=74.

Example: The number of ways 12 boys can travel in three cars so that 4 boys in each car, assuming that three particular boys will not go in the same car.

Solution: First omit three particular boys, remaining 9 boys may be 3 in each car. This can be done in 9 CHOOSE 3 i.e ⁹C₃ ways,

The three particular boys may be placed in three ways one in each car. Therefore total number of ways are =3X⁹C₃.

={9!/3!(9-3)!}X3= 252

so in 252 ways they can be placed.

Example: How many ways did 2 green and 2 black balls come out of a bag containing 7 green and 8 black balls?

Solution: Here bag contains 7 green from that we have to choose 2 so it is 7 CHOOSE 2 problem and 8 black balls from that we have to choose 2 so it is 8 CHOOSE 2 problem.

Hence the Required number = ⁷C₂ X ⁸C₂ = {7!/2!(7-2)!}X{8!/2!(8-2)!}=21X28=588

so in 588 ways we can select 2 green and 2 black from that bag.

Example: Twelve different characters of English words are provided. From these letters, 2 alphabetical names are formed. How many words can be created when at least one letter is repeated.

Solution: here we have to choose 2 letter words from 12 letters so it is 12 CHOOSE 2 problem.

No. of words of 2 letters in which letters have been recurrent any times = 12²

        But no. of words on having two different letters out of 12 =¹²C₂ = {12!/2!(12-2)!} =66

        Required number of words = 12²-66=144-66=78.

Example: There are 12 points on the plane where six are collinear, then how many lines can be drawn by joining these points.

Solution: For 12 points in a plane to make line we require 2 points same for six collinear points, so this is 12 CHOOSE 2 and 6 CHOOSE 2 problem.

The number of lines is = ¹²C₂ – ⁶C₂ +1={12!/2!(12-2)!}-{6!/2!(6-2)!}+1 =66-15+1=52

So in 52 number of ways it lines can be drawn.

Example: Find the numeral of ways in which a 6-member cabinet can be set up from 8 gentlemen and 4 ladies so that the cabinet consists of at least 3 ladies.

Solution: For forming the committee, we can choose from 3 each men and women and 2men 4 women so the problem includes 8 CHOOSE 3, 4 CHOOSE 3, 8 CHOOSE 2 and 4 CHOOSE 4.

Two types of cabinet can be formed

        (i) Having 3 men and 3 ladies

        (ii) Having 2 men and 4 ladies

        Possible no. of ways =  (⁸C₃ X ⁴C₃) + (⁸C₂ X⁴C₄)= {8!/3!(8-3)!}X{4!/3!(4-3)!} +{8!/2!(8-2)!}X{4!/4!(4-4)!} = 56X4+ 28X1 =252      

So In 252 ways we can form such cabinet.

       These are some examples where we can compare the situation of ⁿP_r vs ⁿC_r in the case of permutation, the way things are organized is important. However in Combination the order means nothing.

Conclusion

A brief description of Permutation and combination when repeated and non-repeated with the basic formula and important results is provided in the form of real examples, in this series of articles we will discuss in detail the various outcomes and formulas with relevant examples, if you want to continue reading:

SCHAUM’S OUTLINE OF Theory and Problems of DISCRETE MATHEMATICS

https://en.wikipedia.org/wiki/Permutation

https://en.wikipedia.org/wiki/Combination

For more Article on Mathematics, please follow this Link