In real life, we may encounter many cases in which material is applied to tension or compression in 2 perpendicular direction at that time. The stress applied in such a case is known as biaxial stress. A balloon is a perfect example of it.
These tensile/compressive stresses also produce shear stress in the material. To calculate the net tensile and shear stress produced in the material, a graphical method is used known as Mohr’s Circle for biaxial stress.
Mohr’s circle is an advantageous and easy way to solve stress equations. It gives the information about the stresses on various planes.
Topic of Discussion: Mohr’s Circle
How to Draw Mohr’s Circle | How Do You Plot Mohr’s Circle?
Let us consider a thin sheet subjected to biaxial tension, as shown in the following figure. The normal and shear stress on a plane whose normal n have an angle of ϕ with the x-axis are specified as follows:
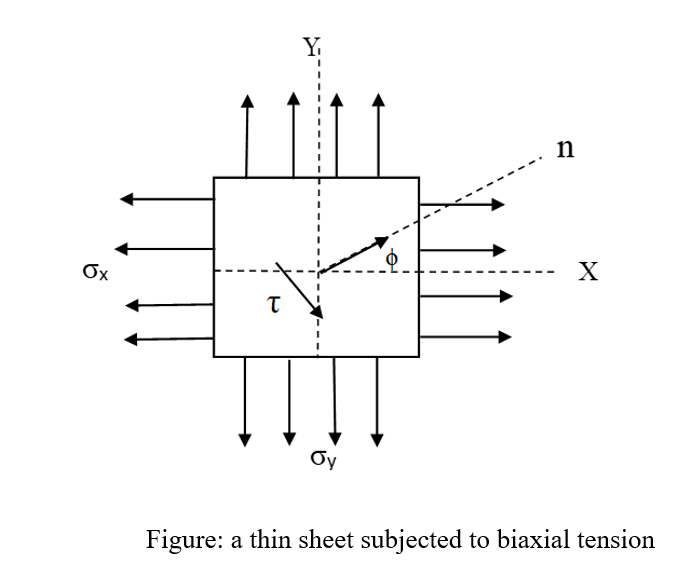
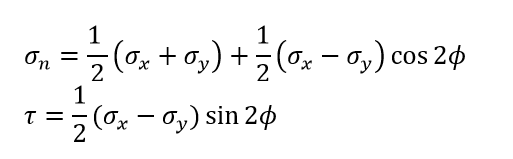
From the above equations, it can be said that these equations can be plotted as a circle in a normal stress-shear stress plane where angle ϕ acts as a parameter.
As we know:
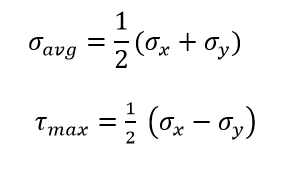
So, normal stress and shear stress can be represented in more compact form as follow:
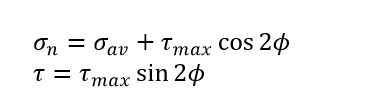
By solving the above equations and eliminating parameter ϕ.
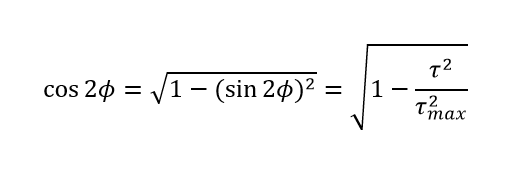
Substitute of this in the first of
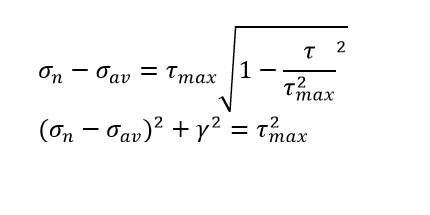
The above equation denotes the standard form of the equation of a circle.
On solving the above equation, we get that radius of the circle formed is
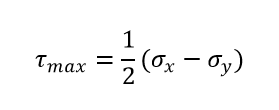
The Center of the circle formed is on σ-axis denoted as
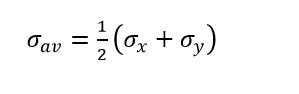
Circle formed on the σ-τ plane with the above parameters is known as Mohr ‘s Circle.
If the applied principal stress applied is of compression kind, it must be taken with the negative sign.
Thus, the origin of Mohr ‘s circle always lies on the σ-axis.
Mohr’s Circle Equations
Following are the standard equations formed of Mohr circle.
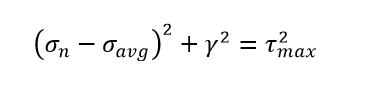
Where,
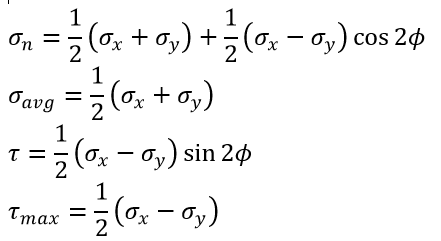
How to Use Mohr’s Circle
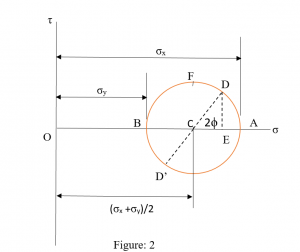
Mohr’s circle is the circle drawn in the plane of σ-τ. σ is on the x-axis, which is the total of the normal force acting on the material. τ is on the y-axis, which is the total shear stress acting on the same plane, hence if we take any point on the Mohr’s circle, its x-coordinate gives the value of total normal stress acting on the material, and y-coordinate gives the value of total shear stress acting on the material.
For figure 2, let’s take a point D on it. The x-coordinate gives the value of total normal stress acting on it, and the y-coordinate gives the value of total shear stress acting on it.
From the geometry, it can be seen that the coordinates of point D are
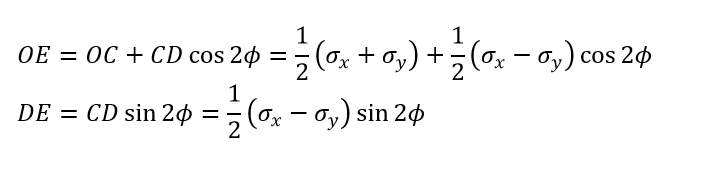
Where OE is an x-coordinate, and DE is a y-coordinate.
For each condition of the material in figure 1 defined by ϕ, there is a corresponding point denoting it on the Mohr’s circle in figure 2.
Let’s say, when ϕ = 0, and normal n coincides the x-axis, and it gives σn = σx
And τ = 0.
When ϕ = 900, the normal n coincides with the x-axis, and it gives σn = σy
And τ = 0.
When ϕ = 450, the normal n coincides with the x-axis, and it gives
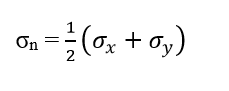
And
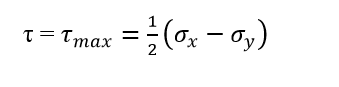
The Mohr’s failure envelope
Failure is the particular value of normal stress or shear stress at which material breaks or develops a crack.
Mohr ’s circle can be used to know the normal and shear stress values at the point of failure.
A material has multiple failure values of shear stresses and normal stresses. Thus, the Mohr Failure Envelope is a locus of all failure such failure points.
For more Details Click Here
Mohr’s Circle Pressure Vessel
The stress experienced by any pressure vessel is the biaxial type of stress. It gives the impression due to pressure experienced by the wall of the pressure vessel can also have stresses generated by the weight of the under pressure fluid inside, its weight, and externally applied load and by an functional torque.
Mohr’s circle is used to denote the stresses developed in the vessel.
Questions and Answers
What is Mohr’s circle used for?
In real life, we may come across many cases in which material is subjected to tension or compression in two perpendicular direction at the identical time. The stress applied in such a case is known as biaxial stress. A balloon is a perfect example of it.
These tensile/compressive stresses also produce shear stress in the material. To calculate the net tensile and shear stress produced in the material, a graphical method is used known as Mohr ‘s Circle for biaxial stress.
What are the principal stresses?
Principal stresses are maximum and minimum stresses at a point on the material. These stresses include only normal stresses and do not include shear stresses.
What are the three principal stresses?
There are mainly three principal stresses as follows:
1) σ1= maximum (most tensile) principal stress
2) σ3= minimum (most compressive) principal stress,
3) σ2= intermediate principal stress.
What is Mohr’s circle of stress?
In real life, we may see numerous cases in which material is subjected to tension or compression in two perpendicular direction at that time. The stress applied in such a case is known as biaxial stress. A balloon is a perfect example of it.
These tensile/compressive stresses also produce shear stress in the material. To calculate the net tensile and shear stress produced in the material, a graphical method is used known as Mohr ‘s Circle for biaxial stress.
What is the radius of Mohr’s circle?
The radius of Mohr’s Circle formed is as follows:
τ_max=1/2(σ_x-σ_y)
To learn more on mechanical engineering articles click here

The lambdageeksScience Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.