How to Find Magnetic Field from Velocity: A Comprehensive Guide

The velocity gradient technique (VGT) is a powerful tool for measuring the direction and intensity of magnetic fields using only the velocity gradients of a fluid. This technique is based on the theory of magnetohydrodynamic (MHD) turbulence, which states that the velocity motions of turbulent fluids are anisotropic, and the direction of anisotropy is determined by the magnetic field surrounding the eddy. In this comprehensive guide, we will delve into the details of the VGT and explore how to use it to find the magnetic field from velocity.

Understanding the Velocity Gradient Technique (VGT)

The VGT captures the detailed magnetic field structure within the turbulent volume under study by tracing the local magnetic field around turbulent eddies, rather than the mean magnetic field. This is because the statistics of Alfvénic turbulence is anisotropic along the local magnetic field, and the velocity gradients also show a distribution of directions in which the most probable orientation of gradients is perpendicular to the magnetic field.

The VGT uses three types of 2D maps to trace magnetic fields:

1. Intensity maps (I(x, y)): These maps are calculated as:
   I(x, y) = ρ(x, y) * v(x, y)
   where ρ is the position-position-velocity (PPV) gas density, and v is the velocity component along the line of sight.

2. Velocity centroid maps (C(x, y)): These maps are calculated as:
   C(x, y) = ∫ v(x, y) * ρ(x, y) / ∫ ρ(x, y) dv
   where ρ is the PPV gas density, and v is the velocity component along the line of sight.

3. Velocity channel maps (Ch(x, y)): These maps are produced by doing an integral along the velocity axis of the PPV cube for all tracers.

In this guide, we will focus on using the intensity maps (I(x, y)) and velocity centroid maps (C(x, y)).

Determining the Magnetic Field Direction

The VGT uses the sub-block-averaging method to predict the direction of the magnetic field through the most probable orientation of gradients within a block. The gradient angle at pixel (x, y) is defined as:

θ(x, y) = arctan[∇C(x, y) / C(x, y)]

This will make up the pixelized gradient field of the spectroscopic data. The direction of the magnetic field can be obtained by rotating the most probable orientation of gradients by 90°.

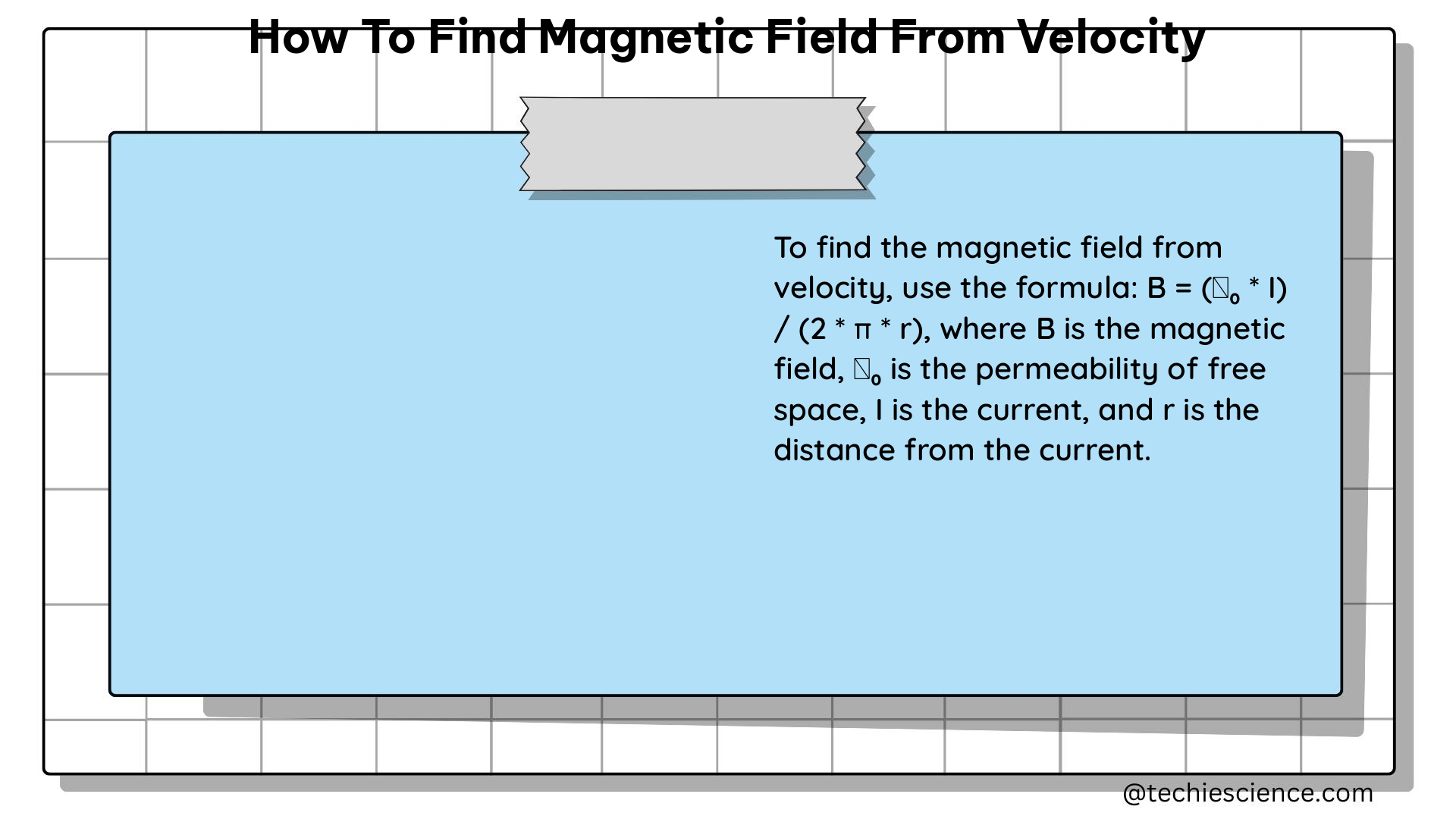
Determining the Magnetic Field Intensity

To determine the magnetic field intensity, we can use the following formula:

B = sqrt(8πρv_A^2)

where:
– B is the magnetic field intensity
– ρ is the gas density
– v_A is the Alfvén velocity, which can be calculated as:

v_A = B / sqrt(4πρ)

To calculate the Alfvén velocity, we need to know the magnetic field strength, which can be obtained using the VGT method described earlier.

Examples and Numerical Problems

Example 1: Calculating the Magnetic Field Direction

Suppose we have the following velocity centroid map (C(x, y)):

x	y	C(x, y)
1	1	10
1	2	12
2	1	8
2	2	11

Using the formula for the gradient angle:

θ(x, y) = arctan[∇C(x, y) / C(x, y)]

We can calculate the gradient angles for each pixel:

• θ(1, 1) = arctan[(12 – 10) / 10] = 0.1963 rad
• θ(1, 2) = arctan[(11 – 8) / 8] = 0.3491 rad
• θ(2, 1) = arctan[(11 – 12) / 12] = -0.0833 rad
• θ(2, 2) = arctan[(8 – 11) / 11] = -0.2808 rad

The most probable orientation of gradients is the direction perpendicular to the magnetic field. Therefore, the direction of the magnetic field is rotated 90° from the most probable orientation of gradients, which is approximately 45° in this example.

Numerical Problem 1: Calculating the Magnetic Field Intensity

Given the following information:
– Gas density (ρ) = 1.2 × 10^-19 kg/m^3
– Alfvén velocity (v_A) = 5 × 10^5 m/s

Calculate the magnetic field intensity (B) using the formula:

B = sqrt(8πρv_A^2)

Solution:

B = sqrt(8π × 1.2 × 10^-19 kg/m^3 × (5 × 10^5 m/s)^2)
B = 3.3 × 10^-9 T

Therefore, the magnetic field intensity is approximately 3.3 × 10^-9 T.

Limitations and Considerations

While the VGT is a powerful tool for measuring magnetic fields from velocity gradients, it is important to consider the following limitations and considerations:

1. Dependence on Turbulence: The VGT relies on the theory of MHD turbulence, which may not always be applicable in certain environments or situations.
2. Sensitivity to Noise: The VGT can be sensitive to noise in the velocity data, which can affect the accuracy of the magnetic field measurements.
3. Comparison with Other Techniques: The VGT results may differ from those obtained using other techniques, such as the Histogram of Relative Orientations (HRO) method, which requires polarimetry data.
4. Validation and Calibration: It is important to validate the VGT results with other independent measurements or simulations to ensure the accuracy of the magnetic field estimates.

Conclusion

The velocity gradient technique (VGT) is a powerful tool for measuring the direction and intensity of magnetic fields using only the velocity gradients of a fluid. By understanding the underlying theory, the calculation of the necessary maps, and the determination of the magnetic field direction and intensity, you can effectively apply the VGT to your research or practical applications. This comprehensive guide has provided you with the necessary knowledge and examples to get started with using the VGT to find the magnetic field from velocity.

References

1. Tracing Magnetic Field Morphology Using the Velocity Gradient Technique, The Astrophysical Journal, 2019
2. Magnetic field, Encyclopedia Magnetica
3. How To Find Magnetic Field From Velocity – YouTube, 2022
4. Determining the Magnitude of the Magnetic Field Some Distance from a Straight Current Carrying Wire, Study.com
5. How is velocity measured in magnetism?, Physics Stack Exchange, 2017