How to Find Magnetic Field from Electric Field: A Comprehensive Guide

In the realm of electromagnetism, understanding the relationship between electric and magnetic fields is crucial. This comprehensive guide will delve into the various methods and principles used to determine the magnetic field (B) from the electric field (E), providing physics students with a detailed and practical resource.

Maxwell’s Equations: The Foundation

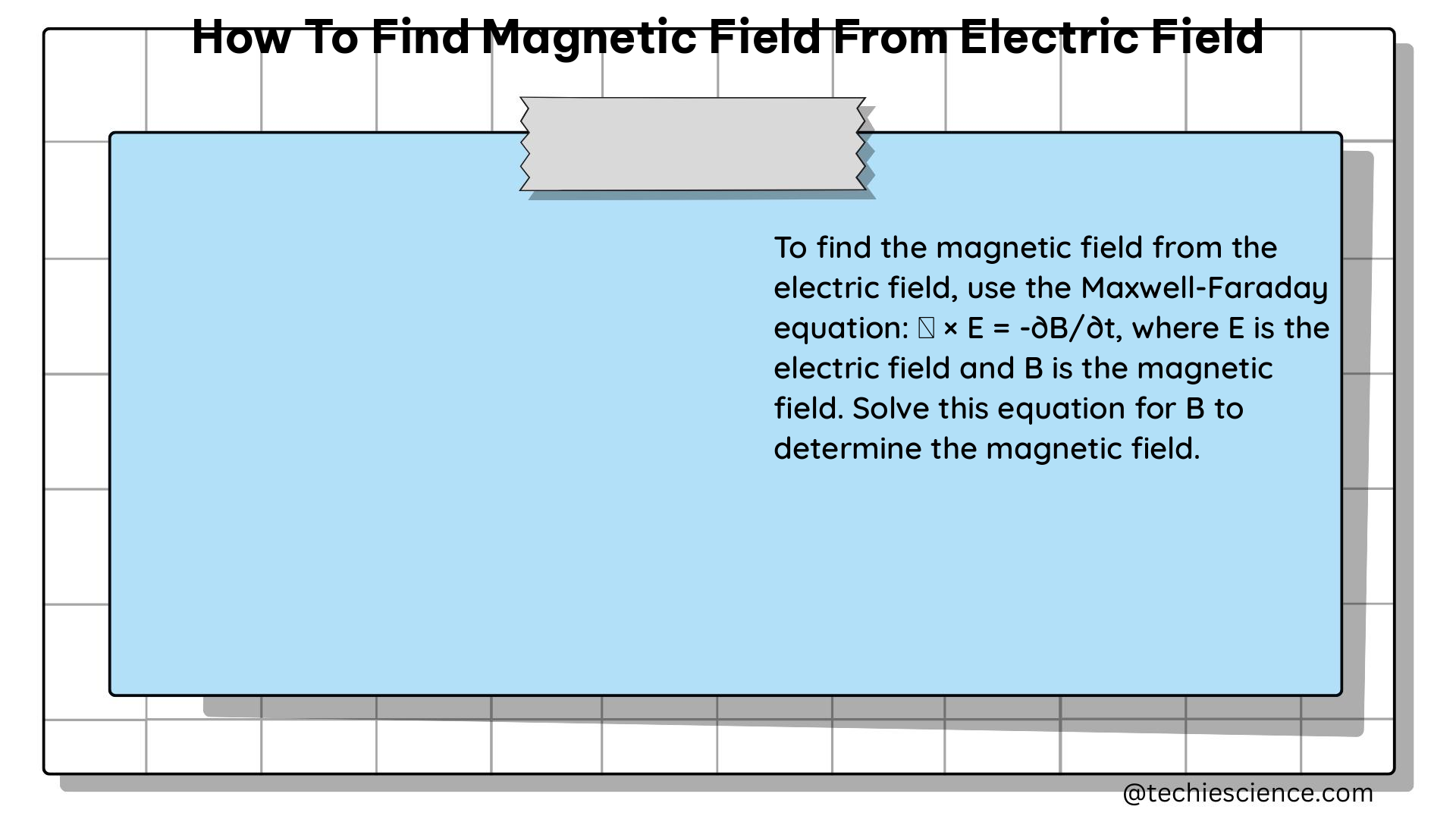
At the heart of finding the magnetic field from the electric field lies Maxwell’s equations, a set of four fundamental equations that describe the interplay between electric and magnetic fields. The equation relevant to this task is:

∇ × E = -∂B/∂t

This equation, known as Faraday’s law of electromagnetic induction, states that the curl of the electric field is equal to the negative partial derivative of the magnetic field with respect to time. This is a differential equation, meaning it operates on infinitesimally small volumes and times. To solve this equation, you’ll need to have a thorough understanding of the electric field as a function of time and space, as well as the ability to perform vector calculus.

Electromagnetic Waves: The Relationship between E and B

In the context of electromagnetic waves, the electric and magnetic fields are intimately related. They are perpendicular to each other and to the direction of propagation, and they are also equal in magnitude, up to a constant factor. This relationship is expressed as:

E = cB

where c is the speed of light. This equation is a direct consequence of Maxwell’s equations and the fact that electromagnetic waves propagate at the speed of light.

Biot-Savart Law: Calculating Magnetic Fields from Currents

Another important tool in finding the magnetic field from the electric field is the Biot-Savart law. This law provides a formula for calculating the magnetic field due to a current. The Biot-Savart law states that the magnetic field at a point is proportional to the integral of the current density (J) over a small volume (dV), divided by the distance from the volume element to the point, all raised to the power of three, and multiplied by the sine of the angle between the current and the line connecting the volume element and the point. Mathematically, this is expressed as:

dB = μ0/4π (J dV x r) / r^3

where μ0 is the permeability of free space, dB is the magnetic field due to the current element, J dV is the current element, r is the vector from the current element to the point, and x denotes the cross product.

Measuring Magnetic Fields

In terms of quantifiable data, the magnetic field can be measured using various instruments, such as magnetometers, SQUIDs (Superconducting Quantum Interference Devices), and Hall probes. These instruments can measure the magnetic field in units of Tesla (T), Gauss (G), or nanotesla (nT). The precision and accuracy of these measurements depend on the specific instrument and the conditions under which the measurement is made.

Practical Application: Calculating Magnetic Field from Electric Field in Electromagnetic Waves

In the context of electromagnetic waves, the magnetic field can be calculated directly from the electric field using the formula:

B = E / c

This formula is a direct consequence of the relationship between E and B fields in electromagnetic waves, as discussed earlier.

Theorem, Formulas, and Examples

To further solidify your understanding, let’s explore some key theorems, formulas, and examples related to finding the magnetic field from the electric field.

Theorem: Faraday’s Law of Electromagnetic Induction

Faraday’s law of electromagnetic induction states that the electromotive force (EMF) induced in a closed loop is equal to the negative of the time rate of change of the magnetic flux through the loop. Mathematically, this is expressed as:

∇ × E = -∂B/∂t

This is the same equation we encountered earlier, which is the foundation for finding the magnetic field from the electric field.

Formula: Biot-Savart Law

The Biot-Savart law, as mentioned earlier, is a formula for calculating the magnetic field due to a current. The formula is:

dB = μ0/4π (J dV x r) / r^3

where μ0 is the permeability of free space, dB is the magnetic field due to the current element, J dV is the current element, r is the vector from the current element to the point, and x denotes the cross product.

Example: Calculating Magnetic Field from Electric Field in an Electromagnetic Wave

Consider an electromagnetic wave propagating in the z-direction with an electric field given by:

E = E0 cos(kz – ωt) î

where E0 is the amplitude of the electric field, k is the wavenumber, ω is the angular frequency, and î is the unit vector in the x-direction.

Using the relationship between the electric and magnetic fields in an electromagnetic wave, we can calculate the magnetic field as:

B = E / c
B = (E0 cos(kz – ωt) î) / c
B = (E0 / c) cos(kz – ωt) ĵ

where ĵ is the unit vector in the y-direction.

This example demonstrates how the magnetic field can be directly calculated from the given electric field using the relationship between E and B in electromagnetic waves.

Numerical Problems and Data Points

To further enhance your understanding, let’s consider some numerical problems and data points related to finding the magnetic field from the electric field.

Problem 1: Calculating Magnetic Field from Electric Field in a Transmission Line

A transmission line has an electric field of 1000 V/m in the x-direction. Calculate the corresponding magnetic field in the y-direction.

Given:
– Electric field, E = 1000 V/m in the x-direction
– Speed of light, c = 3 × 10^8 m/s

Using the relationship between E and B in electromagnetic waves:
B = E / c
B = (1000 V/m) / (3 × 10^8 m/s)
B = 3.33 × 10^-6 T in the y-direction

Data Point: Typical Values of Electric and Magnetic Fields

In a typical electromagnetic wave, such as a radio wave or a microwave, the electric and magnetic field strengths can vary widely depending on the source and the distance from the source. Here are some typical values:

• Electric field strength: 1 V/m to 1000 V/m
• Magnetic field strength: 3.33 × 10^-9 T to 3.33 × 10^-6 T

These values can be used to estimate the magnetic field from the electric field, or vice versa, using the relationship between E and B in electromagnetic waves.

Conclusion

In this comprehensive guide, we have explored the various methods and principles used to determine the magnetic field (B) from the electric field (E) in the realm of electromagnetism. By understanding Maxwell’s equations, the relationship between electric and magnetic fields in electromagnetic waves, and the Biot-Savart law, you can now confidently apply these concepts to calculate the magnetic field from the electric field in a variety of contexts. Remember to utilize the provided theorems, formulas, examples, and numerical problems to solidify your understanding and become proficient in this essential skill.

References

1. Determining the Magnitude of the Magnetic Field Some Distance from a Straight Current Carrying Wire: https://study.com/skill/learn/determining-the-magnitude-of-the-magnetic-field-some-distance-from-a-straight-current-carrying-wire-explanation.html
2. How do you find the magnetic field corresponding to an electric field?: https://physics.stackexchange.com/questions/41900/how-do-you-find-the-magnetic-field-corresponding-to-an-electric-field
3. Electric field control of magnetism: https://royalsocietypublishing.org/doi/10.1098/rspa.2020.0942
4. Energetic Communication: https://www.heartmath.org/research/science-of-the-heart/energetic-communication/
5. EM WAVES| JEE MAIN| FINDING MAGNETIC FIELD FROM ELECTRIC FIELD: https://www.youtube.com/watch?v=kYp9rInlwvA